Нахождение интегралов в среде Pascal
Текст задания: найти интеграл функции sin (x+10)+x4=0 используя два метода: метод прямоугольников и метод трапеций; пользователь вводит значения и выбирает метод решения.
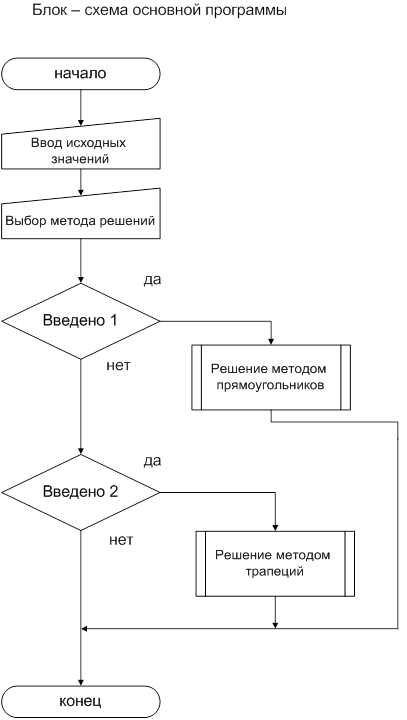
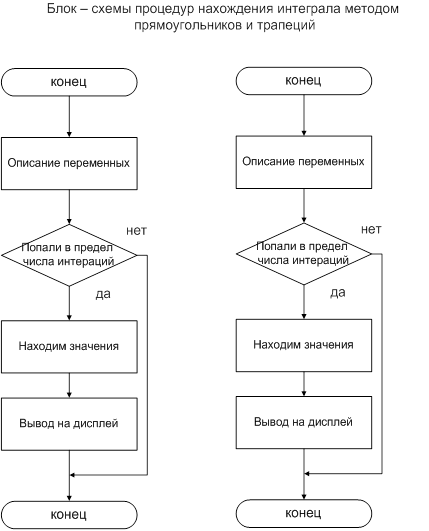
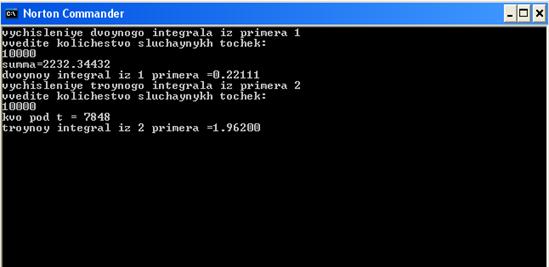
Текст программы:
program LW_5;
uses
Crt;
var
dx, x1, x2, e, i, c, s:real;
function Fx (x:real):real;
begin
Fx:=sin (x+10)+x*x*x*x; {function}
end;
procedure CountViaBar;
var
xx1, xx2:real;
c:longint;
begin
writeln ('–');
writeln ('–>MEthod PRYAMOUGOL''NIKOVVVV');
writeln ('vsego interaciy:', round (abs(x2-x1)/e));
i:=0;
for c:=1 to round (abs(x2-x1)/e) do begin
write ('integration ', c, chr(13));
xx1:=Fx (x1+c*e);
xx2:=Fx (x1+c*e+e);
i:=i+abs (xx1+xx2)/2*e;
end;
writeln ('–');
writeln ('INTEGRAL=', i);
end;
procedure CountViaTrap;
var
xx1, xx2, xx3:real;
c:longint;
begin
writeln ('–');
writeln ('–>MEthod TRAPECIY');
writeln ('vsego interaciy:', round (abs(x2-x1)/e));
i:=0;
for c:=1 to round (abs(x2-x1)/e) do begin
write ('Integration ', c, chr(13));
xx1:=Fx (x1+c*e);
xx2:=Fx (x1+c*e+e);
if xx2>xx1 then xx3:=xx1 else xx3:=xx2;
i:=i+abs (xx2-xx1)*e+abs(xx3)*e;
end;
writeln ('–');
writeln ('INTEGRAL=', i);
end;
begin
clrscr;
writeln ('vvedite ishodniye zna4eniya:');
write ('NA4AL''NOYE ZNE4ENIYE x (x1)='); Readln(x1);
write ('KONE4NOYE ZNA4ENIYE x (x2)='); Readln(x2);
write ('TO4NOST'' VbI4ISLENIY (e)='); Readln(e);
writeln ('–======vvedite metod====== – :');
writeln ('DLYA METODA PRYAMOUGOL''NIKOV VVEDITE 1, DLYA METODA TRAPECIY VVEDITE 2');
//writeln ('DLYA METODA TRAPECIY VVEDITE 2');
readln (s);
if s=1 then begin
CountViaBar;
end;
if s=2 then begin
CountViaTrap;
end;
readln;
end.
Похожие работы
... 2-3 Поиск литературы 7 1 7 2-4 Разработка модели разветвленной СМО 6 1 6 3 Поиск литературы завершен 3-6 Изучение литературы по теории массового обслуживания 10 1 10 4 Модель разработана 4-5 Разработка алгоритма программы 10 1 10 5 Алгоритм программы разработан 5-7 Выбор среды программиро-вания и создание программы 30 1 ...
... Впрочем, для наиболее распространённых псевдослучайных чисел период столь велик, что превосходит любые практические потребности. Подавляющее большинство расчётов по методу Монте-Карло осуществляется с использованием псевдослучайных чисел. Значения любой случайной величины можно получить путём преобразования значений одной какой-либо случайной величины. Обычно роль такой случайной величины играет ...
... . Уравнение (2; 0,1) с оператором А, обладающим указанными свойствами, будем называть операторным уравнением первого рода, или, короче,— уравнением первого рода. 2.1. Метод подбора решения некорректно поставленных задач 2.1.1. Широко распространенным в вычислительной практике способом приближенного решения уравнения (2; 0,1) является метод подбора. Он состоит в том, что для элементов z ...
... деятельности во внешней речи про себя и этап выполнения деятельности в форме внутренней речи. Данные характеристики деятельности и этапы ее становления и определяют требования к составлению обучающих программ. 2. При оценке авторской технологии проверяйте ее на соответствие признакам педагогической (методической) технологии Классификационные параметры технологии По уровню применения: ...
0 комментариев