Курсовая работа
по дисциплине
Исследование операций
Руководитель:
Плотникова Н. В.
«____» ___________ 2005 г.
Автор:
Студент группы ПС-346
Попов А. Е..
«____» ___________ 2005 г.
Работа защищена
с оценкой
«____» ___________ 2005 г.
Оглавление
1 Условия задач. 3
2 Решение задач исследования операций. 4
2.1 Решение задачи 1. 4
2.2 Решение задачи 2. 8
2.3 Решение задачи 3. 12
2.4 Решение задачи 4. 17
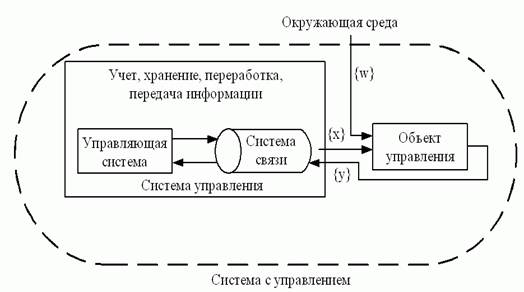
1 Условия задач
2 Решение задач исследования операций 2.1 Решение задачи 1
Для составления математической модели задачи введём переменные:
![]() – количество горючего, доставляемое со склада A на бензоколонку 1
– количество горючего, доставляемое со склада A на бензоколонку 1
![]() – количество горючего, доставляемое со склада A на бензоколонку 2
– количество горючего, доставляемое со склада A на бензоколонку 2
x3a – количество горючего, доставляемое со склада A на бензоколонку 3
x1b – количество горючего, доставляемое со склада B на бензоколонку 1
x2b – количество горючего, доставляемое со склада B на бензоколонку 2
x3b – количество горючего, доставляемое со склада B на бензоколонку 3
x1c – количество горючего, доставляемое со склада C на бензоколонку 1
x2c – количество горючего, доставляемое со склада C на бензоколонку 2
x3c – количество горючего, доставляемое со склада C на бензоколонку 3
На складах A, B, C находится 90, 60, 90 тонн горючего соответственно, следовательно, можно записать:

На каждую заправку нужно оправить одинаковое количество горючего, равное (90+60+90)/3:

В соответствии со стоимостями перевозок запишем целевую функцию, которую необходимо минимизировать:
![]()
Имеем классическую транспортную задачу с числом базисных переменных, равным n+m–1 , где m–число пунктов отправления, а n – пунктов назначения. В решаемой задаче число базисных переменных равно 3+3-1=5.
Число свободных переменных соответственно 9-4=4.
Примем переменные x1a, x1b, x2a, x2с, x3с в качестве базисных, а переменные x1c, x2b, x3а, x3b в качестве свободных (данный выбор позволяет легко выразить базисные переменные через свободные).
Далее в соответствии с алгоритмом Симплекс метода необходимо выразить базисные переменные через свободные:
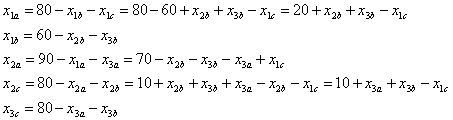
Следующий шаг решения – представление целевой функции через свободные переменные:
 В задании требуется найти минимум функции L. Так как коэффициент при переменной x1c меньше нуля, значит найденное решение не является оптимальным.
В задании требуется найти минимум функции L. Так как коэффициент при переменной x1c меньше нуля, значит найденное решение не является оптимальным.
Составим Симплекс таблицу:
| bi | x3a | x2b | x3b | x1c | |
| L | 630 -10 | -3 1 | -1 0 | -4 4 | 1 -1 |
| x1a | 20 -10 | 0 1 | -1 0 | -1 1 | 1 -1 |
| x1b | 60 0 | 0 0 | 1 0 | 1 0 | 0 0 |
| x2a | 70 10 | 1 -1 | 1 0 | 1 -1 | -1 1 |
| x2c | 10 10 | -1 -1 | 0 0 | -1 -1 | 1 1 |
| x3c | 80 0 | 1 0 | 0 0 | 1 0 | 0 0 |
Выбор в качестве разрешающей строки х2с обусловлен тем, что именно в этой строке отношение свободного члена к переменной х1с минимально. Выполним необходимые преобразования над элементами Симплекс таблицы:
| bi | x3a | x2b | x3b | x2c | |
| L | 620 | -2 | -1 | 0 | -1 |
| x1a | 10 | 1 | -1 | 0 | -1 |
| x1b | 60 | 0 | 1 | 1 | 0 |
| x2a | 80 | 0 | 1 | 0 | 1 |
| x1c | 10 | -1 | 0 | -1 | 1 |
| x3c | 80 | 1 | 0 | 1 | 0 |
Все коэффициенты при свободных переменных неположительные, следовательно, найденное решение является оптимальным. Запишем его:
x1a=10; x1b=60; x1c=10;
x2a=80; x2b=0; x2c=0;
x3a=0; x3b=0; x3c=80;
L=620;
Для проверки правильности вычислений можно составить транспортную таблицу:
| A | B | C | ||
| 1 | 10 | 60 | 10 | 80 |
| 2 | 80 | 0 | 0 | 80 |
| 3 | 0 | 0 | 80 | 80 |
| 90 | 60 | 90 |
После анализа таблицы можно сделать вывод, что вычислительных ошибок при расчетах сделано не было.
Ответ:
x1a=10 x1b=60 x1c=10
x2a=80 x2b=0 x2c=0
x3a=0 x3b=0 x3c=80
L=620
2.2 Решение задачи 2Составим систему ограничений исходя из условия задачи

Целевая функция задачи имеет вид:
![]()
Пусть переменные x1 и x2 - свободные, а переменные x3, x4 и x5 – базисные.
Далее необходимо представить систему ограничений в стандартном виде. Для этого проведем ряд преобразований:
![]()
Подставим выражения для x3 и x4 в третье уравнение системы ограничений:
![]()
Упростим полученное выражение и выразим x5:
![]()
Теперь можно представить систему ограничений в стандартном виде:

Необходимо также выразить целевую функцию через свободные переменные:
![]()
Теперь можно заполнить Симплекс-таблицу
| bi | x1 | x2 | |
| L | 1 | -1 | -3 |
| x3 | 2 | -1 | 2 |
| x4 | 2 | 1 | 1 |
| x5 | 1 | 1 | -1 |
Исходя из того, что все свободные члены положительны, можно сделать вывод о том принятое решение является опорным.
Далее нужно выбрать разрешающий элемент. В качестве разрешающего столбца целесообразно принять столбец x1, так как коэффициент при x1 в целевой функции меньше коэффициента при x2. Разрешающей строкой будет строка x5, так как отношение свободного члена этой строки к коэффициенту при x1 минимально. Отметим найденный разрешающий элемент в таблице, а также заполним необходимые клетки:
| bi | x1 | x2 | |
| L | 1 1 | -1 1 | -3 -1 |
| x3 | 2 1 | -1 1 | 2 -1 |
| x4 | 2 -1 | 1 -1 | 1 1 |
| x5 | 1 1 | 1 1 | -1 -1 |
Перерисуем таблицу с учётом замены x2 на x3:
| bi | x5 | x2 | |
| L | 2 | 1 | -4 |
| x3 | 3 | 1 | 1 |
| x4 | 1 | -1 | 2 |
| x1 | 1 | 1 | -1 |
Коэффициент при х2 в целевой функции отрицателен, значит необходимо произвести ещё одну замену. В качестве разрешающей строки примем x3. Таким образом, разрешающим будет элемент, стоящий на пересечении строки x3 и столбца x2.
| bi | x5 | x2 | |
| L | 2 12 | 1 4 | -4 4 |
| x3 | 3 3 | 1 1 | 1 1 |
| x4 | 1 -6 | -1 -2 | 2 -2 |
| x1 | 1 3 | 1 1 | -1 1 |
В итоге получим:
| bi | x5 | x3 | |
| L | 14 | 5 | 4 |
| x2 | 3 | 1 | 1 |
| x4 | -5 | -1 | 0 |
| x1 | 4 | 2 | 1 |
Коэффициенты при свободных переменных в целевой функции положительны, значит, найденное решение является оптимальным.
Ответ:
x1=4
x2=3
x3=0
x4=-5
x5=0
L=14
2.3 Решение задачи 3Условие задачи задано в виде транспортной таблицы:
| ПН ПО | B1 | B2 | B3 | запасы |
| A1 | 50 | 15 | 10 | 300 |
| A2 | 21 | 30 | 20 | 100 |
| A3 | 18 | 40 | 25 | 200 |
| A4 | 23 | 22 | 12 | 800 |
| A5 | 25 | 32 | 45 | 200 |
| заявки | 500 | 300 | 800 |
Применим к задаче метод «Северо-Западного угла». Для этого заполним таблицу начиная с левого верхнего угла без учёта стоимости перевозок:
| ПН ПО | B1 | B2 | B3 | запасы |
| A1 | 300 | 300 | ||
| A2 | 100 | 100 | ||
| A3 | 100 | 100 | 200 | |
| A4 | 200 | 600 | 800 | |
| A5 | 200 | 200 | ||
| заявки | 500 | 300 | 800 |
В таблице заполнено n+m-1=7 клеток, значит найденное решение является опорным. Далее необходимо улучшить план перевозок в соответствии со стоимостями доставки грузов. Для этого используем циклические перестановки в тех циклах, где цена отрицательна.
| ПН ПО | B1 | B2 | B3 | запасы |
| A1 | 50 300 | 15 | 10 | 300 |
| A2 | 21 100 | 30 | 20 | 100 |
| A3 | 18 100 | 40
|
| 200 |
| A4 | 23 |
200 |
600 | 800 |
| A5 | 25 | 32 | 45 200 | 200 |
| заявки | 500 | 300 | 800 |
В данной таблице в верхней части ячейки указана стоимость перевозки, а в нижней количество перевозимого груза. Прямоугольником выделен отрицательный цикл γ1=25+22-40-12=-5. Минимальное значение перевозок, стоящих в отрицательных вершинах равно k1=100. В итоге получим уменьшение стоимости перевозки:
ΔL1=-5*100=-500
Транспортная таблица примет следующий вид:
| ПН ПО | B1 | B2 | B3 | запасы |
| A1 | 50 300 | 15 | 10 | 300 |
| A2 | 21 100 | 30 | 20 | 100 |
| A3 | 18 100 | 40 | 25 100 | 200 |
| A4 | 23 | 22
| 12
| 800 |
| A5 | 25 |
|
200 | 200 |
| заявки | 500 | 300 | 800 |
γ2=12+32-45-22=-23 k2=200 ΔL2=-23*200=-4600
| ПН ПО | B1 | B2 | B3 | запасы |
| A1 | 50
| 15 |
| 300 |
| A2 | 21 100 | 30 | 20 | 100 |
| A3 | 18
| 40 | 25
| 200 |
| A4 | 23 | 22 100 | 12 700 | 800 |
| A5 | 25 | 32 200 | 45 | 200 |
| заявки | 500 | 300 | 800 |
γ3=10+18-50-25=-47 k3=100 ΔL3=-47*100=-4700
| ПН ПО | B1 | B2 | B3 | запасы |
| A1 | 50
| 15 | 10
| 300 |
| A2 | 21 100 | 30 | 20 | 100 |
| A3 | 18 200 | 40 | 25 | 200 |
| A4 |
| 22 100 |
700 | 800 |
| A5 | 25 | 32 200 | 45 | 200 |
| заявки | 500 | 300 | 800 |
γ4=10+23-12-50=-29 k4=200 ΔL4=-29*200=-6800
| ПН ПО | B1 | B2 | B3 | запасы |
| A1 | 50 | 15 | 10 300 | 300 |
| A2 | 21 100 | 30 | 20 | 100 |
| A3 | 18 200 | 40 | 25 | 200 |
| A4 | 23 200 | 22 100 | 12 500 | 800 |
| A5 | 25 | 32 200 | 45 | 200 |
| заявки | 500 | 300 | 800 |
Отрицательных циклов в транспортной таблице больше нет. Следовательно, можно предположить, что найденное решение является оптимальным. Для проверки применим метод потенциалов.
Составим систему:

Положим β2=0, тогда α4=-22
β1=1, α2=-20
β3=-10, α2=-22
α1=-20, α5=-32
Все коэффициенты α отрицательны, значит, найденный план перевозок является оптимальным.
Ответ:
x21=100;
x31=200;
x41=200;
x42=100;
x52=200;
x13=300;
x43=500.
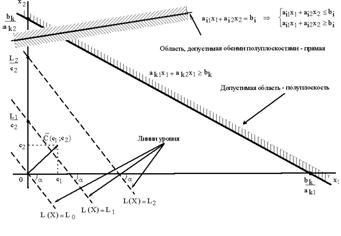
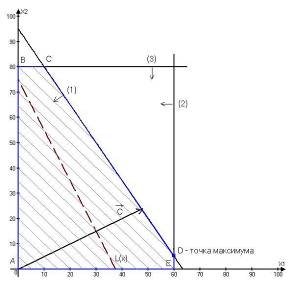
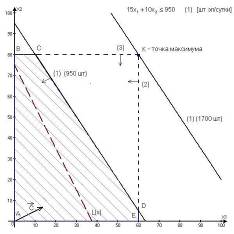
2.4 Решение задачи 4Составим математическую модель поставленной задачи.
Найти минимум функции f(x1,x2)
![]()
При ограничениях 
Заменив знак функции f(x1,x2) на противоположный, перейдем к поиску максимума функции:
![]()
Теперь задача приведена к стандартному виду задачи квадратичного программирования. Приступим к решению.
1) Определим стационарную точку

Решив систему, получим:
x1=10
x2=7
Очевидно, что данные координаты не удовлетворяют условиям ограничений. Поэтому проверять стационарную точку на относительный максимум нет необходимости.
2) Составим функцию Лагранжа:
![]()
Применив к функции Лагранжа теорему Куна-Таккера, будем иметь систему:
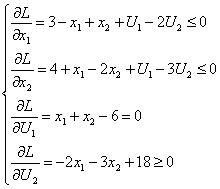
3) Преобразуем полученную систему:

Из уравнения 3 системы следует, что x2=6-x1:

Для обращения неравенств системы в равенства введём V1, V2, W и преобразуем систему:

4) Запишем условия дополняющей нежесткости:

5) Введем в систему уравнений искусственные переменные z1,z2:

Поставим задачу максимизации функции ![]() .
.
Для решения этой задачи воспользуемся Симплекс-методом. Примем переменные z1 и z2 в качестве базисных:

![]()
Составим Симплекс таблицу:
| bi | x1 | U1 | U2 | V1 | V2 | |
| φ | -17M 0 | -5M 0 | 0 0 | M 0 | M 0 | -M 0 |
| z1 | 9 8 | 2 3 | -1 1 | 2 -3 | -1 0 | 0 1 |
| z2 | 8 8 | 3 3 | 1 1 | -3 -3 | 0 0 | 1 1 |
| W | 0 0 | -1 0 | 0 0 | 0 0 | 0 0 | 0 0 |
| bi | x1 | z2 | U2 | V1 | V2 | |
| φ | -17M 17M | -5M M | 0 M | M -M | M -M | -M M |
| z1 | 17 17/5 | 5 1/5 | 1 1/5 | -1 -1/5 | -1 -1/5 | 1 1/5 |
| U1 | 8 -51/5 | 3 -3/5 | 1 -3/5 | -3 3/5 | 0 3/5 | 1 -3/5 |
| W | 0 17/5 | -1 1/5 | 0 1/5 | 0 -1/5 | 0 -1/5 | 0 1/5 |
| bi | z1 | z2 | U2 | V1 | V2 | |
| φ | 0 | M | M | 0 | 0 | 0 |
| x1 | 17/5 | 1/5 | 1/5 | -1/5 | -1/5 | 1/5 |
| U1 | -11/5 | -3/5 | -2/5 | 1/2 | 3/5 | -2/5 |
| W | 17/5 | 1/5 | 1/5 | -1/5 | -1/5 | 1/5 |
В итоге получим
x1=17/5
x2=6-x1=13/5
Как видно, координаты стационарной точки сильно отличаются от координат, полученных в качестве ответа. Это можно объяснить тем, что стационарная точка не удовлетворяет условиям ограничений.
Условия дополняющей нежесткости
 выполняются.
выполняются.
Следовательно, найденное решение является оптимальным.
Найдем значения целевой функции:
![]() =- 51/5 - 52/5 + 289/50 – 221/25 + 169/25 =
=- 51/5 - 52/5 + 289/50 – 221/25 + 169/25 =
= -16.9
Ответ:
x1 = 17/5
x2 = 13/5
f(x1,x2) = -16.9
Похожие работы
... в различных условиях (разработка перспективных планов). Такой выбор является наиболее трудным. Он требует выявления основных факторов, влияющих на будущие последствия решения, взвешивания всех "за" и "против". Сама технология принятия управленческого решения в уникальных ситуациях будет подробно рассмотрена в разделе 2, после того, как будут раскрыты основные этапы процесса принятия решения. 2. ...
... и эксплуатацию подавляющего большинства ЛС. И этот факт предопределяет проблему прогнозирования затрат, цен, тарифов, т.е. рост капитальных вложений в перспективе требует оценки эффективности их в соответствующем периоде. 5. Методы решения логистических задач Научную базу логистики составляет широкий спектр методов, разработанных в рамках различных дисциплин. Перечислим некоторые из них. ...
... игр, теория массового обслуживания, и др. 1. ПОСТАНОВКА ЗАДАЧИ Целью нашего курсового проекта является решение задачи линейного программирования графическим методом. 1.1 Математическое программирование. Математическое программирование ("планирование") – это раздел математики, занимающийся разработкой методов отыскания экстремальных значений функции, на аргументы которой наложены ...
... , 6) сетевого планирования и управления, 7) выбора маршрута, 8) комбинированные. Из перечисленных выше методов математического программирования наиболее развитым и законченным является линейное программирование. В его рамки укладывается широкий круг задач исследования операций. Линейное программирование Несмотря на требование линейности целевой функции и ограничений, в рамки линейного ...
 300
300
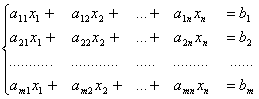
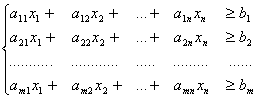
0 комментариев