Зміст
Моделювання економіки. Транспортна задача.
Список використаної літератури
Моделювання економіки. Транспортна задача
Опишемо як вирішуються транспортні задачі та наведемо приклад рішення за допомогою надбудови „Поиск решения” у MS Excel.
Нехай існує [m] пунктів, у яких зосереджено деякий однорідний вантаж. Номер пункту зосередження [i] = 1,m. Нехай відома кільккість вантажу, що знаходиться у кожному пункті зосередження [ai]. Цей вантаж треба доставити до [n] пунктів споживання. Номер пункту споживання [j]=1,n. Нехай відома потреба [bij] у цьому вантажі у кожному пункті споживання. Також відомі питомі витрати на перевезення вантажу з i-того пункту зосередження до j-того пункту споживання [cij]. Треба визначити, скільки вантажу треба везти з кожного з пунктів зосередження до кожного з пунктів споживання таким чином, щоб з кожного пункту зосередження загалом вивозилоси не більше, ніж там є, а до кожного пункту споживання не менше від потреби (![]() ), і загальна вартість перевезень була якомога меншою.
), і загальна вартість перевезень була якомога меншою.
Розв’язок:
Позначимо невідомі обсяги перевезень з кодного пункту зосередження до кожного пункту споживання [xij]. Отже, умова про те, що загальна кількість вантажу, вивезена з кожного пункту зосередження, не перевищує кільксітвантажу в ньому:
![]()
Умова про те, що потреба кожного пункту споживання має задовільнятися:
![]()
Обсяги перевезень між кожним пунктом зосередження і споживання – невід’мні величчини:
![]()
Розглянуті нерівності визначають деяку множину, до якої належить багато варіантів перевезень. Серед цих варіантів треба обрати такі, що мінімізували б функцію:
![]()
(пошук умовного мінімуму для функції багатьох змінних).
Приклад
Заводи деякої автомобільної фірми розміщено у містах А, В, С та D. Основні центри розподілення продукції сконцентровано у містах 1, 2, 3 та 4. Обсяги виробництва заводів наведено у таблиці, так само як величини попиту у центрах розподілення. Вартість перевезення автомобілів залізницею по кожному із маршрутів або час перевезення по кожному із маршрутів наведено у таблиці.
Побудуйте математичну модель, яка дозволить визначити кількість автомобілів, що перевозиться з кожного заводу у кожен розподільчий центр, та оптимальний план перевезень таким чином, щоб загальні транспортні витрати були мінімальними.
| Пункт | 71 |
| Місто А | 1000 |
| Місто В | 1300 |
| Місто С | 1400 |
| Місто D | 800 |
| Розподільчий центр (РЦ) у місті 1 | 1300 |
| РЦ у місті 2 | 1500 |
| РЦ у місті 3 | 500 |
| РЦ у місті 4 | 1200 |
| Пункт | Критерій оптимальності – вартість перевезення автомобілів, $/шт |
| 71 | |
| A-1 | 150 |
| A-2 | 95 |
| A-3 | 100 |
| A-4 | 50 |
| B-1 | 65 |
| B-2 | 45 |
| B-3 | 55 |
| B-4 | 130 |
| С-1 | 65 |
| С-2 | 80 |
| С-3 | 75 |
| С-4 | 65 |
| D-1 | 55 |
| D-2 | 80 |
| D-3 | 60 |
| D-4 | 40 |
Для рішення задачі побудуємо її математичну модель.
Невідомими є обсяги перевезень. Нехай xij – обсяги перевезень з і-го постачальника до j-го продавця. Цільовою функцією є залежність вартості від розміру партії постачання:
![]() (1),
(1),
де cij – вартості перевезень с i-го постачальника до j-го продавця.
Цільова функція
F = 150x11 + 95x12 + 100x13 +50x14 + 65x21 +45x22 +55x23 +130x24 +65x31 + 80x32 +75x33 +65x34 +55x41 +80x42 +60x43 +40x44 → min.
Крім цього, невідомі повинні задовольняти таким обмеженням:
- ненегативність обсягів постачань
xij≥0.
- розглянемо модель типу:
![]() ,
, ![]()
Розмістимо дані ситуаційної задачі в спеціальній таблиці:
| Покупці Постачальники | 1 | 2 | 3 | 4 | Виробництво |
| А | 150 | 95 | 100 | 50 | 1000 |
| B | 65 | 45 | 55 | 130 | 1300 |
| C | 65 | 80 | 75 | 65 | 1400 |
| D | 55 | 80 | 60 | 40 | 800 |
| Попит | 1300 | 1500 | 500 | 1200 |
У клітинах, що стоять на перетині постачальника й покупця, ставимо довільні цифри, відстань від споживача до постачальника.
Перевіримо ситуацію на баланс:
Виробництво = 1000 + 1300 + 1400 + 800 = 4500
Попит = 1300 + 1500 + 500 + 1200 = 4500
Баланс виконується, тому не треба додавати фіктивні пункти споживання чи попиту.
Побудуємо план перевезень методом північно-західного кута:
| Покупці Постачальники | а | б | в | г | Виробництво |
| А | 1000 | 1000 | |||
| B | 300 | 1000 | 1300 | ||
| C | 500 | 500 | 400 | 1400 | |
| D | 800 | 800 | |||
| Попит | 1300 | 1500 | 500 | 1200 |
Розрахуємо середню вартість, на яку перевозиться вантаж:


Ще раз побудуємо план:
| ПокупціПостачальники | а | б | в | г | Виробництво |
| А | 1000 | 1000 | |||
| B | 300 | 800 | 200 | 1300 | |
| C | 200 | 700 | 300 | 200 | 1400 |
| D | 800 | 800 | |||
| Попит | 1300 | 1500 | 500 | 1200 |
Розрахуємо середню вартість:

Як бачимо, другий план значно краще, вартісь перевезення вантажу скоротилася на 18,89 $.
Для перевірки оптимальності складеного плану перевезень скористаємося надбудовою „Поиск решения” MS Excel (рис.1.1 і.1.3).
До комірки F10 внесено формулу =СУММ(B10:E10) і простягнуто її до комірки F13, до комірки В14 внесено формулу =СУММ(B10:B13) і простягнуто її до комірки Е14. До цільовій комірці G14 введено формулу (1) у вигляді виразу =СУММПРОИЗВ(B4:E7;B10:E13).
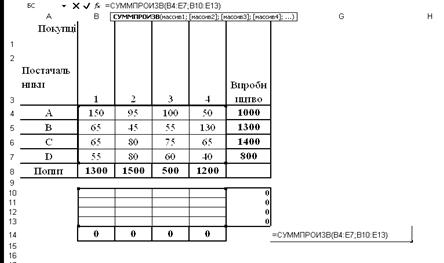
Рис.1.1.
На рис.1.2. наведено внесення обмежень моделі у діалоговому вікні надбудови „Поиск решения”.


Рис.1.3.
Розрахуємо середню вартість:

Як бачимо, останній план значно краще, вартісь перевезення вантажу скоротилася на 23,11 $.
Список використаної літератури
1. Николин В.И. Автотранспортный процесс и оптимизация его элементов. - М.: Транспорт, 1990.
2. Боборыкин В.А. Математические методы решения транспортных задач. - Л.: СЗПИ, 1986.
3. Геронимус Б.А. Экономико-математические методы в планировании на автомобильном транспорте. - М.: Транспорт, 1982.
4. Аникин Б.А., Тяпухин А.П. Коммерческая логистика // Издательство Велби. М.: – 2005. – 432 с.
0 комментариев