Министерство образования Российской Федерации
Тульский государственный университет
Кафедра "Инструментальные и метрологические системы"
ИНФОРМАТИКА
ПРОГРАММНО-МЕТОДИЧЕСКИЙ КОМПЛЕКС
"Вычисление определенного интеграла
методом трапеций"
Выполнил:
студент гр.621721 /Я.И. Зыбина/
Тула 2003
Аннотация
Разработанный программно-методический комплекс содержит математическое описание, алгоритм и программу вычисления определенного интеграла методом трапеций, производит расчет n значений исследуемой функции и выводит их в виде таблицы. Программа написана на языке Бейсик и работает в диалоговом режиме. Исходные данные вводятся с клавиатуры.
Содержание
Аннотация
Общие сведения
Функциональное назначение
Описание логической структуры алгоритм решения задачи
Используемые технические и программные средства
Входные и выходные данные
Приложения
Перечень терминов и сокращений
Перечень ссылочных документов
Общие сведения
Обозначение данной программы - YANA. bas. Наименование программы - вычисление определённого интеграла методом трапеции. Данная программа разработана на языке Basic и работает в среде программирования QB. EXE в диалоговом режиме. Для нормального функционирования программы обязательно наличие операционной системы Windows, любого файлового менеджера (FAR, N. C)
Функциональное назначение
Программа предназначена для вычислении определенного интеграла методом трапеций с заданной точностью. Рассчитывает значения функции с равномерным шагом и выводит их в виде таблицы, что позволяет производить анализ исследуемого уравнения. Результаты расчета выводятся на экран монитора.
Описание логической структуры алгоритм решения задачи
Логическая структура программы может быть представлена следующей последовательностью действий.
На первом этапе выдается наименование программы и выводятся сообщения о необходимости ввода данных с клавиатуры:
a - начальное значение интервала для расчета значений;
b - конечное значение интервала для расчета значений;
ee - точность вычислений (0.01%)
Поскольку точность расчетов зависит от числа разбиений n исходного отрезка [a,b], то вычислительный процесс целесообразно строить итерационным методом, увеличивая n до тех пор пока не будет выполнено условие:
|Ik-Ik-1| < ee.
Первоначально n задается минимальным, следовательно размер шага будет максимальным: h= (b-a) /n.
Полученный интеграл от x=a равен нулю. Далее n будет увеличиваться, пока разность между промежуточными интегралами не станет максимально приближенной к нулю (f1=f2). Это означает, что вычисления имеют минимальную погрешность.
Подробную схему программы смотри приложение 1.
По данной - схеме разработана программа на языке Бейсик, использующая принципы структурного программирования. Программа смотри приложение 2.
Используемые технические и программные средства
Для работы программы требуется любой IBM совместимый компьютер, видео-адаптер SVGA, печатающее устройство. Операционная система MS DOS, драйвер для поддержки русских букв и среда программирования QuickBASIC версии 4.5
Входные и выходные данные
Входными данными для расчета являются:
исследуемая функции для реализации программы методом трапеций;
a - начальное значение интервала для расчета значений;
b - конечное значение интервала для расчета значений функции;
n - количество расчетных точек;
h - величина шага изменения аргумента;
e - точность вычислений по аргументу.
Результатами вычислений являются:
таблица аргументов и значений исследуемой функции;
значение определенного интеграла.
Результаты расчета приведены в приложении 3 для заданной функции.
Приложения
Приложение 1
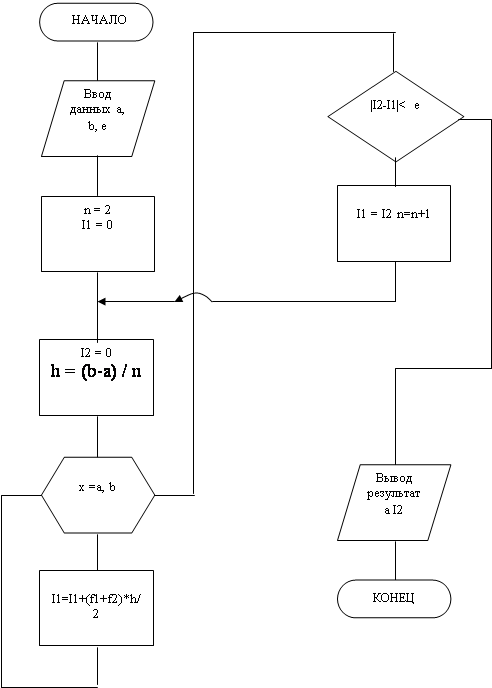
Приложение 2
REM Задать уравнение в виде fny(x)=0
DEF fny (x) = (1 / SQR (2 * 3.1415)) * EXP (-x * x / 2)
REM Очистить экран
CLS
REM Вывести назначение программы
PRINT "========================================"
PRINT "¦ Программа вычисления определенного интеграла ¦"
PRINT "¦ методом трапеций ¦"
PRINT "--------------------------------------------------------------------"
PRINT "¦ Курсовая работа по дисциплине 'ИНФОРМАТИКА' ¦"
PRINT "========================================"
INPUT " Начальное значение интервала для расчета значений а=",a
INPUT " Конечное значение интервала для расчета значений b=", b
h = (b – a)/n
PRINT "------------------------------------"
PRINT "| x | | y(x) |"
PRINT "------------------------------------"
FOR x = a TO b STEP h
PRINT USING " | ##. ### | " ; x; FNy (x)
NEXT x
PRINT "------------------------------------"
e = 1
INPUT " введите число разбиений n= '', n
I1 = 0
I2=0
h = (b – a)/n
FOR x = a TO b STEP h
f1=FNy(x)
f2 = FNy (x+h)
IF x <> a THEN I1 =I1+ (f1 + f2) * h /2
f1 = f2
NEXT x
e = (ABS (I2 – I1)) * 100 / I
WEND
PRINT USING “определённый интеграл = ##. ###### ” ; I1
NEXT x
PRINT " Таблица значений исследуемой функции"
PRINT " ====================== "
PRINT " ¦ n/n ¦Аргумент¦ Значение ¦ "
PRINT " ====================== "
REM Закончить работу программы
STOP
END
Приложение 3
¦ Программа вычисления корней уравнения ¦
¦ методом простых итераций ¦
---------------------------------------------------------------------
¦ Курсовая работа по дисциплине 'ИНФОРМАТИКА' ¦
=========================================
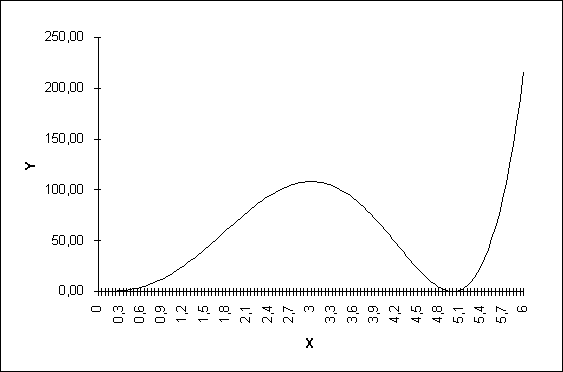
Таблица значений исследуемой функции
======================
¦ n/n ¦Аргумент¦ Значение ¦
======================
¦ 1 ¦ 0.000 ¦ 0 ¦
¦ 2 ¦ 0.500 ¦ 3.5299 ¦
¦ 3 ¦ 1.000 ¦ 1.2131 ¦
¦ 4 ¦ 1.500 ¦ 0.4328 ¦
¦ 5 ¦ 2.000 ¦ 0.1353 ¦
¦ 6 ¦ 2.500 ¦ 0.0351 ¦
¦ 7 ¦ 3.000 ¦ 0.0074 ¦
¦ 8 ¦ 3.500 ¦ 0.0012 ¦
¦ 9 ¦ 4.000 ¦ 0.16 · 10-3 ¦
¦ 10 ¦ 4.500 ¦ 0.18 · 10-4 ¦
¦ 11 ¦ 5.000 ¦ 0.149 · 10-5 ¦
¦ 12 ¦ 5.500 ¦ 0.98 · 10-7 ¦
¦ 13 ¦ 6.000 ¦ 0.5 · 10-8 ¦
¦ 14 ¦ 6.500 ¦ 0.206 · 10-9 ¦
¦ 15 ¦ 7.000 ¦ 0.654 · 10-12 ¦
¦ 16 ¦ 7.500 ¦ 0.162 · 10-12 ¦
¦ 17 ¦ 8.000 ¦ 0.317 · 10-14 ¦
¦ 18 ¦ 8.500 ¦ 0.482 · 10-16 ¦
¦ 19 ¦ 9.000 ¦ 0.573 · 10-18 ¦
¦ 20 ¦ 9.500 ¦ 0.532 · 10-20 ¦
======================
Перечень терминов и сокращений
Аннотация -краткое разъяснение и содержание данной работы.
Алгоритм - конечная последовательность точно определенных действий, приводящих к однозначному решению поставленной задачи.
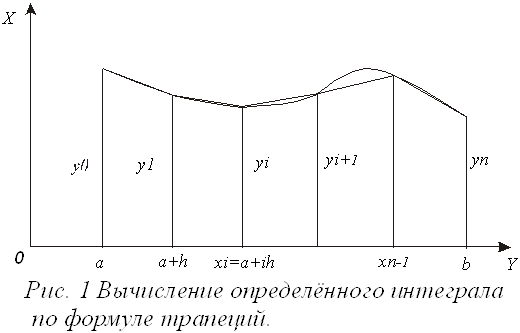
Интеграл (определенный) - в математике обозначает предел суммы y0dx0+y1dy1+…+yn-1dxn-1, выраженный числом. (Напротив, неопределенный интеграл есть функция)
Программа-описание процесса обработки информации на языке программирования, определяющего последовательность обработки.
Трапеция-четырехугольник, имеющий две параллельные стороны (основания) и боковые стороны.
bas-расширение Q. Basic
. cdr-расширение Corel Draw
Перечень ссылочных документов
1. ГОСТ 7.1-84. Библиотечное описание документа. Общие требования.
2. ГОСТ 19.401 - 78. Текст программы
3. ГОСТ 19.402 - 78. Описание программы Сборник 133а, Единая система программной документации.
4. Еганов В.М., Качурин Н.М., Коряков А.Е., Туляков С.П. Основы информатики. Учебное пособие. - ТулГУ, Тула
5. Жигарев А.Н. и др. Основы компьютерной грамоты / А.Н. Жигарев, Н.В. Макарова, М.А. Путинцева; Под общ. ред. Н.В. Макаровой. - Л.: Машиностроение. Ленингр. отд-ние, 1987. - 255 с.
6. Сборник 133а, Единая система программной документации.
| Лист регистрации изменений | |||||||||
| Номера листов (страниц) | Всего листов (страниц) в докум. | № документа | Входящий № сопроводительного докум. и дата | Подп. | Дата | ||||
| Изм | измененных | Замененных | новых | Аннулированных | |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Похожие работы
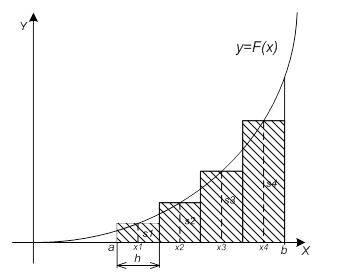
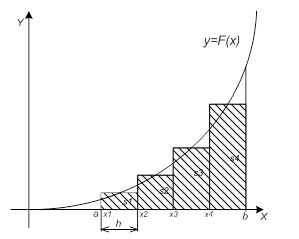
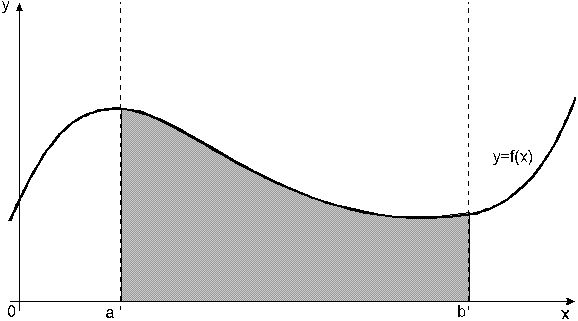
ределенный интеграл функции типа численно представляет собой площадь криволинейной трапеции ограниченной кривыми x=0, y=a, y=b и y= (Рис. 1). Есть два метода вычисления этой площади или определенного интеграла — метод трапеций (Рис. 2) и метод средних прямоугольников (Рис. 3). Рис. 1. Криволинейная трапеция. Рис. 2. Метод трапеций. Рис. 3. Метод средних прямоугольников. По методам ...
... n (увеличения числа интеграций) повышается точность приближенного вычисления интегралов Задание на лабораторную работу 1) Написать программы вычисления определенного интеграла методами: средних, правых прямоугольников, трапеции и методом Симпсона. Выполнить интегрирование следующих функций: 1. f(x)=x f(x)=x2 f(x)= x3 f(x)= x4 на отрезке [0, 1] с шагом , , 2. f(x)= f(x)= f(x)= ...
... процедура TABL ) и интеграл. 4. Заключение и выводы. Таким образом очевидно, что при вычислении определенных интегралов с помощью квадратурных формул, а в частности по формуле Чебышева не дает нам точного значения, а только приближенное. Чтобы максимально приблизиться к достоверному значению интеграла нужно уметь правильно выбрать метод и формулу, по которой будет вестись расчет. Так же ...
... , т. е. знакопостоянна. рис. 2 Для выполнения поставленной задачи составлена нижеописанная программа, приближенно вычисляющая определенный интеграл с помощью формулы Симпсона. Программа состоит из трех функций main, f и integral. Функция main вызывает функцию integral для вычисления интеграла и распечатывает на экране результат. Функция f принимает аргумент x типа float и возвращает значение ...




0 комментариев