IV Гомельская научно-практическая конференция школьников по математике, ее приложениям и информационным технологиям "Поиск"
Учебно-исследовательская работа
«Генерация дидактических материалов по математике»
Ученицы11/А класса
ГУО СОШ№22 г. Гомеля
Прохоренко Елены АлександровныНаучный руководитель –
Горский Сергей Михайлович, учитель математики Государственного учреждения образования СОШ №22 г.Гомеля
Гомель, 2009
Содержание
Введение
1 Описание работы программы
1.1 Запуск программ
1.2 Описание файла шаблона
2 Использование постобработчиков
Заключение
Список использованных источников
Приложение 1
ВведениеНа данный момент некоторые преподаватели уже пытались привлечь компьютер к составлению самостоятельных работ, контрольных работ, домашних заданий. Наиболее формализуемые и параметризуемые задачи относятся к таким предметам как математика, физика, химия. В литературе приведены примеры генерации заданий по математике для квадратных уравнений, по геометрии на объемы и поверхности тел вращения, по химии на концентрации растворов, по физике на решение треугольников (векторы сил в механике). Однако в описанных примерах каждая работа создается отдельной программой, вид параметризованных формул "вшит" в программный код и недостаток данного подхода отмечается даже самими авторами [2].
В данной работе излагается метод генерации произвольных задач с решениями, позволяющий избежать колоссальных трудозатрат по верстке и составлению задач, а также демонстрируется программа генерации заданий по математике, удовлетворяющих условиям различности и равноценности. Отличие предлагаемого метода от методов, реализованных, в уже существующих программах заключается в том, что пользователю предоставляется механизм создания параметризованных задач и аппарат для их клонирования (создание нескольких вариантов). То есть клонируемые задачи не обязаны подходить под определенный тип, а число вариантов задается во внешнем файле-сценарии или определяется через условия, накладываемые на параметры.
Следует заметить, что в большинстве существующих программ предлагается генерировать только задания для последующего их распечатывания. Наличие отдельного напечатанного варианта при проведении контрольной или самостоятельной работы имеет ряд преимуществ перед отсутствием такового: например, решается проблема списывания — каждый учащийся вынужден обрабатывать свои данные. Есть и свои недостатки — учителю затем нужно проверить не 2 варианта, а 25–30.
Разработанная мною программа устраняет этот недостаток, поскольку она позволяет включать в текст задачи и решение, и ответ, которые выносятся в отдельный файл.
Так же программа поддерживает написание тестов, с перемешиванием вариантов ответов в каждом варианте теста и позволяет производить выбор между различными однотипными, но различными по шаблону заданиями.
Поскольку программа работает с текстовыми файлами, то она позволяет
- составлять шаблоны файлов в различных форматах, близких к plain text (LaTeX, MathML+HTML),
- проводить обработку иными средствами, такими как MatLab, Mathematica и др.
- при создании специализированного языка разметки, задачи, генерируемые данной программой, могут быть использованы в интерактивном режиме, реализуя не только функции проверки определенной темы, но для реализации режима «подсказки», для дифференциации заданий для учащихся (если учащийся не решил данную задачу, предложить более легкую).
Данная программа широко используется для подготовки контрольных и самостоятельных работ в 5–7 классах ГУО СОШ№ 22 г. Гомеля.
1 Описание работы программы
Программа, являющаяся скриптом, написана на языке программирования Python 2.4. Данный язык является свободно распространяемым интерпретатором, а свободно распространяемая программа py2exe позволяет создать из скрипта программу для систем семейства Windows. Текст скрипта приведен в приложении 1.
1.1 Запуск программыДля запуска программы необходимо в командной строке набрать команду ex2. количество вариантов имя файла шаблона имя файла. После выполнения программы появится файл имя файла.txt содержащий текст сгенерированных вариантов и файл имя файла answ.txt содержащий ответы к файлам.
1.2 Описание файла шаблонаФайл шаблона является обычным plain-text файлом, содержащим строки с маркерами в начале строки.
Маркер code означает, что после него идет инициализация переменных используемых в тексте шаблона.
Маркер отв. означает, что строка, содержащая маркер переходит в файл с ответами.
Маркер choice означает, что из заданий и ответов, разделенных символом ` следует выбрать случайным образом только один.
Маркер test означает, что варианты ответов для теста, разделенные символом ` следует перемешать, правильный вариант должен быть помечен символом !. В файл с заданием переноситься все варианты ответов, а в файл с ответами номера правильных.
При инициализации переменных можно использовать все арифметические операции (/ — деление, * — умножение), все математические функции в американской нотации, следующие специальные функции:
· abs(x) — модуль числа,
· pow(x,y[,m]) — возведение x в степень y по модулю m,
· math.sqrt(x) — квадратный корень из x,
· round(n[,z]) — округление чисел до заданного знака после (до) точки,
· random.random() — случайное число из диапазона [0;1),
· random.randrange([start,]stop[,step]) — выдает случайное число из диапазона [start,stop) с интервалом step (по умолчанию step=1, start=0),
· условный оператор if условие : оператор
· del переменная удаляем переменную
· s.replace(‘что-то’, ‘чем-то’) замена в строке s “что-то” “чем-то”.
Пример файла шаблона
code a=random.randrange(100)+10
code b=random.randrange(100)+10
code c=random.randrange(100)+10
2. Найдите неизвестный член пропорции x:{a}={b}:{c}.
При необходимости ответ округлите.
отв 2.
test {c*b/a}`{c*c/b}`!{a*b/c}`{a/b/c}
Данный шаблон генерирует следующее задание:
2. Найдите неизвестный член пропорции x:17=97:63.
При необходимости ответ округлите.
1) 26 2) 40 3) 0 4) 359
2. Использование постобработчиков
В случае, когда составляемое задание содержит более сложные с точки зрения математики проблемы, программа для его генерации будет довольно громоздкой. Значительно облегчить процесс генерации заданий позволит система компьютерной алгебры Mathematica фирмы Wolfram Research, Inc. Этот программный продукт является признанным мировым лидером среди множества компьютерных инструментов, используемых в научных исследований и в педагогическом процессе. С помощью этой системы легко осуществлять широкий спектр символьных преобразований, в том числе и в сфере математического анализа (дифференцирование, интегрирование). Она позволяет решать уравнения, находить пределы, строить разнообразные графики и многое другое.
Mathematica позволяет пользователю писать программы на ее встроенном языке, поддерживая при этом различные стили программирования — как функциональный, так и процедурный. В данной заметке не затрагиваются вопросы программирования собственно в среде Mathematica. Нас будет интересовать возможность взаимодействия этой программы с файлами, содержащими команды разметки TeX. В такие файлы (а также, в файлы, содержащие программы на языках C или Fortran) можно вставлять выражения системы Mathematica, ограничивая их, слева и справа комбинаций знаков <* и *>. Получившийся файл обрабатывается системой Mathematica, которая заменяет заключенное между этими символами выражение на результат его вычисления.
Файл, содержащий команды разметки языка TeX и функции системы Mathematica, должен иметь расширение mtex. При обработке такого файла командой Splice[], сформировавшийся результат будет автоматически сохранен в файл с расширением tex.
Например, пусть файл task2.mtex содержит следующий фрагмент текста:
Рассмотрим неравенство
$\dfrac{<*u=(3x-5)(x+4); v=(x+4)(x-5); PolynomialRemainder[u,-v,x]*>}
{<*Expand[-v]*>}
\leqslant <*-PolynomialQuotient[u,-v,x]*>.$ \hfill $(*)$
\bigskip
и эквивалентное ему
$\dfrac {(3x-5)(x+4)}{(x+4)(x-5)}\geqslant 0.$ \hfill $(**)$
Тогда после выполнения команды Splice["task2.mtex"] автоматически
созданный файл task2.tex уже будет содержать результат выполнения функций системы Mathematica:
![]() Рассмотрим неравенство
Рассмотрим неравенство

$\dfrac{40 + 10\,x}
{20 + x - {x^2}}
\leqslant 3.$ \hfill $(*)$
\bigskip
и эквивалентное ему
$\dfrac {(3x-5)(x+4)}{(x+4)(x-5)}\geqslant 0.$ \hfill $(**)$
В данном примере использовались следующие функции системы Mathematica:
Expand[v] — раскрывает скобки в выражении v;
PolynomialRemainder[u,v,x] — вычисляет остаток от деления многочлена u(x) на многочлен v(x);
PolynomialQuotient[u,v,x] — находит частное от деления этих многочленов.
Результат обработки данного файла программой TeX показан на врезке.
Заключение
Существует потребность в создании интерактивных систем, где задача диалога с учеником и проверка решения ложится на компьютер. Диалоговое взаимодействие обеспечивает следующие аспекты обучения: непрерывный контроль деятельности обучаемого, диагностирование, управление системой со стороны самого обучаемого.
Поэтому я в дальнейшем планирую написать программу, реализующую указанные возможности.
Список использованных источников1. Г. Россум, Язык программирования Python. / Г. Россум, Ф.Л.Дж. Дрейк, Д.С. Откидач, М. Задка, М. Левис, С. Монтаро, Э.С. Реймонд, А.М. Кучлинг, М.-А. Лембург, К.-П.Йи, Д. Ксиллаг, Х.Г. Петрилли, Б.А. Варсав, Дж.К. Ахлстром, Дж. Роскинд, Н. Шеменор, С. Мулендер.— 2001 — 454 c.
2. Шестаков А.П., Генерация дидактических материалов по математике, // http://comp-science.narod.ru
Приложение 1# -*- coding: cp1251 -*-
#
# запуск:
# имя_программы количество_вариантов файл_шаблона
# файл_заданий
#
import re
import random
import math
import sys
import string
n=int(sys.argv[1]) # считываем количество вариантов
templet=sys.argv[2] # считываем имя файла шаблона
output=sys.argv[3] # считываем имя файла вывода заданий
problems=open(output+'.txt','w') # открываем файл заданий для
# записи
answers=open(output+'_answ.txt','w')
pattern=r"\{(.+?)\}" # создаем регулярное выражение
expression=re.compile(pattern)
for i in range(1,n+1): # цикл по количеству вариантов
task=open(templet,'r') # открываем шаблон
problems.write('Вариант '+str(i)+'\n')
answers.write('Вариант '+str(i)+'\n')
for line in task:
if line.find('code ')>-1: # инициализация переменных в
шаблоне
line=line.replace('code ','')
exec line
else:
k=expression.findall(line) # замена выражения его
значением
for element in k:
line=line.replace(element,str(eval(element)))
line=line.replace('{','') # косметическое удаление
# фигурных скобок
line=line.replace('}','')
if line.find('отв ')>-1:
line=line.replace('отв ','')
answers.write(line)
elif line.find('test ')>-1: # обработка вариантов
тестового задания
line=line.replace('test ','')
line=line.replace('\n','')
test=line.split("`")
random.shuffle(test)
for i in range(0,len(test)):
if test[i].find('!')>-1:
test[i]=test[i].replace('!','')
problems.write(str(i+1)+') '+test[i]+' ')
answers.write(str(i+1)+'\n')
else:
problems.write(str(i+1)+') '+test[i]+' ')
problems.write('\n')
elif line.find('choice ')>-1: # обработка вариантов
# выбора
line=line.replace('choice ','')
line=line.replace('\n','')
variant=line.split("`")
num=2*random.randrange(round(len(variant)/2))
problems.write(variant[num]+'\n')
answers.write(variant[num+1]+'\n')
else:
problems.write(line)
problems.write('\n\n')
answers.write('\n\n')
task.close
problems.close
answers.close
Похожие работы
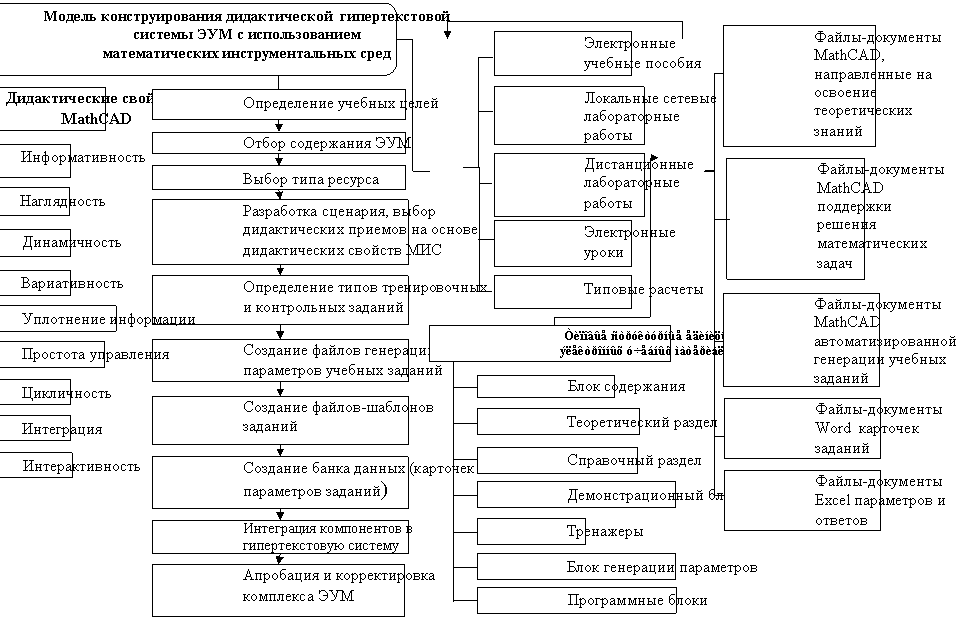
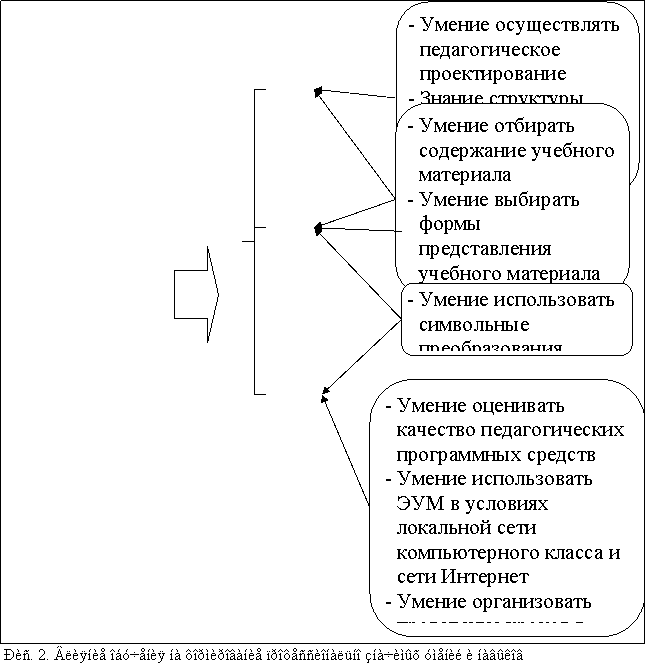
... системы электронных учебных материалов на основе технологии конструирования ЭУМ в среде MathCAD Происходит формирование умений и навыков конструирования электронных учебных материалов в среде MathCAD на творческом уровне В системе профессиональной подготовки учителей математики, физики, информатики недостаточно отражены подходы к созданию и применению электронных учебных материалов с ...
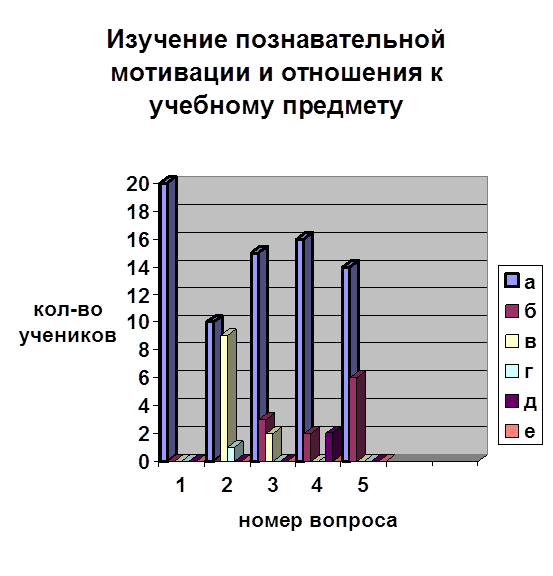
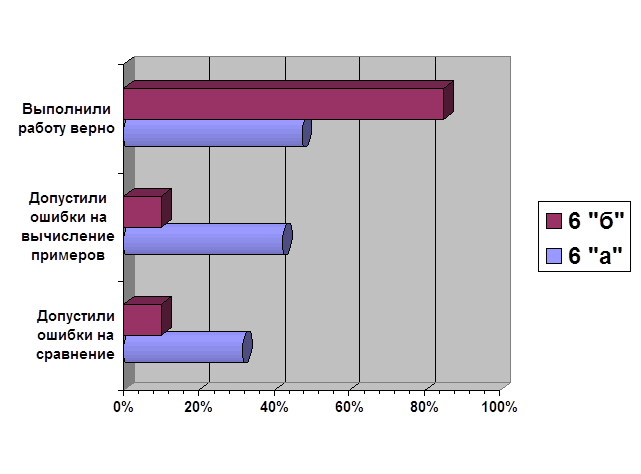
... дидактических игр на уроках математики, анализ игровой деятельности Изучив теоретические материалы по развитию мотивации познавательной деятельности, у автора возникло желание и интерес реализации этого на практике. Для того чтобы доказать или опровергнуть, что использование дидактических игр на уроках математики активизирует познавательную деятельность учащихся, автором работы в 6 «б» ...
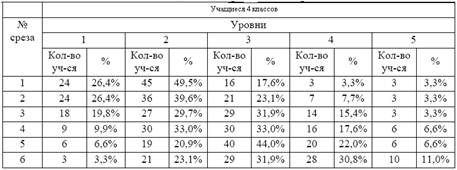
... 5 человек; низкий уровень мышления (6 баллов) – 4 человека. Далее переходим ко второму этапу эксперимента – формирующему. Описанию которого посвятим п.3.2. 3.2. ИСПОЛЬЗОВАНИЕ ПРОБЛЕМНЫХ СИТУАЦИЙ НА УРОКАХ МАТЕМАТИКИ В РАЗВИТИИ ТВОРЧЕСКОГО МЫШЛЕНИЯ УЧАЩИХСЯ В последнее время учителя начальных классов довольно часто при изучении математики создают на уроках проблемные ситуации. Однако чаще всего ...
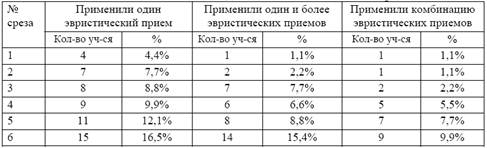
... в уровне развития от 4 до 38%, что подтверждает соответствующую часть гипотезы исследования. Таким образом, проведенное исследование доказало эффективность использования эвристической технологии в образовательном процессе школы. Заключение В результате нашего исследования нами было рассмотрено понятие "эвристическая технология", определены характерные особенности эвристической технологии в ...



0 комментариев