Спектральные характеристики

Спектральные характеристики

Демидов Р.А., ФТФ, 2105
Введение

В первой части работы я поставил себе цель описать линейные операторы в целом, а также подробно рассказать о важной характеристике спектра операторов – спектральном радиусе.

В этой части работы я подробнее остановлюсь на не менее важной характеристике спектров – резольвенте, и расскажу о связи этой характеристики с подвидами спектра оператора – с остаточным, точечным и непрерывными его частями. Вначале, опять же, необходимо остановиться на некоторых основных определениях и понятиях теории линейных операторов. Итак:

-           Пусть A - оператор, действующий в конечномерном линейном пространстве E. Спектром оператора называется множество всех его собственных значений.

-           Квадратную матрицу n×n можно рассматривать как линейный оператор в n-мерном пространстве, что позволяет перенести на матрицы «операторные» термины. В таком случае говорят о спектре матрицы.

-           Пусть A - оператор, действующий в банаховом пространстве E над полем k. Число λ называется регулярным для оператора A, если оператор R(λ) = (A − λI)^-1, называемый резольвентой оператора A, определён на всём E и непрерывен.

-           Множество регулярных значений оператора A называется резольвентным множеством этого оператора, а дополнение резольвентного множества - спектром этого оператора.

-           Максимум модулей точек спектра оператора A называется спектральным радиусом этого оператора и обозначается через r(A). При этом выполняется равенство:

Это равенство может быть принято за определение спектрального радиуса,приусловии существования данного предела.

Теперь рассмотрим состав самого спектра. Он неоднороден, и состоит из следующих частей:

-           дискретный (точечный) спектр - множество всех собственных значений оператора A - только точечный спектр присутствует в конечномерном случае;

-           непрерывный спектр - множество значений λ, при которых резольвента (A - λI)^-1 определена на всюду плотном множестве в E, но не является непрерывной;

-           остаточный спектр - множество точек спектра, не входящих ни в дискретную, ни в непрерывную части.

Таким образом, мы видим, что спектр оператора состоит из 3-х больших частей, принципиально различных.

Свойства резольвенты

Теорема 1: ограничен. Тогда  является регулярной точкой.

Доказательство. . Пусть. Тогда .

- банахово, , причем он ограничен:

Резольвента существует и ограничена. Чтд.

Теорема 2: не принадлежит точечному спектру осуществляет биекцию на .

Доказательство.

ð   Если построена биекция, то не существует , за исключением тривиальной.

ð   Если - точка точечного спектра, то , что противоречит биективности .

Теорема 3: (Тождество Гильберта)

Доказательство.

,,

,верно => Чтд.

 

Следствия:

1)          - коммутативность резольвенты.

2)          (т.к. непрерывна по в точке ), т.е. она бесконечно дифференцируема (аналитическая функция).

Итак, - аналитическая оператор-функция на множестве регулярных точек (резольвентном множестве). - разложение в ряд Лорана (имеет место при , но, возможно, и в большей области).

Упражнение: (Примеры вычисления спектрального радиуса)

 

,

.

Возьмем.Тогда

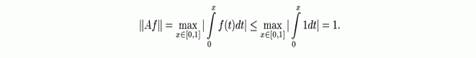
Таким образом . Эта оценка достижима при  , т.е. ,и r_c(A)=1.

Теорема 4: всякая к.ч , есть регулярная точка самосопряженного оператора A.

Доказательство.

] регулярная точка, значит не собственное значение и . Проверим ограниченность .

ограничен,  и его можно распространить на с сохранением нормы оператора, так как  не собственое значение. Если при этом  не замкнуто, то  не замкнут. При этом линейный оператор, обратный к замкнутому, а также сопряженный к нему, замкнут => самосопряженный оператор замкнут.

Спектральная теория в электронике

Полезнейшим приложением спектральной теории в физике является теория спектров электрических сигналов. Суть теории состоит в том, что любой сигнал на входе линейной цепи возможно представить совокупностью гармонических колебаний, или тестовых сигналов, заданной частоты, вопрос такого разложения состоит в нахождении амплитуд результирующих колебаний. Последние вычисляются определенным образом.

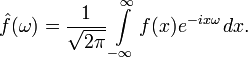
Классическое преобразование Фурье представляет из себя линейный оператор.

Спектральная теория здесь работает следующим образом – для периодических входных сигналов для нахождения соответствующих амплитуд используется интегральное преобразование – дискретный Фурье- образ:

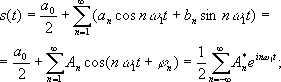
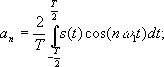
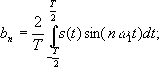
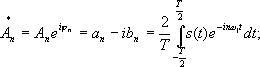
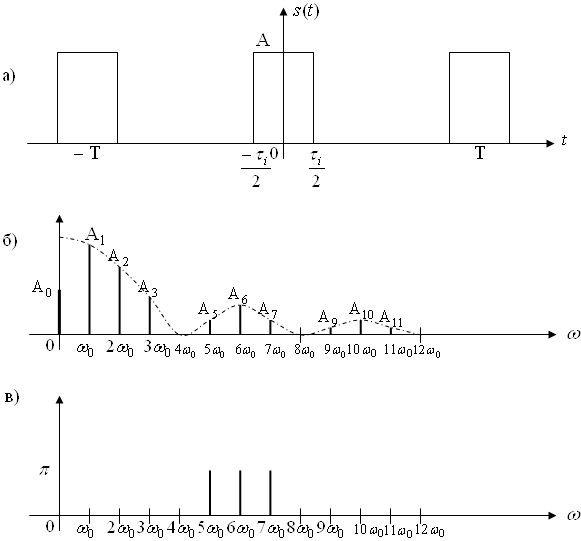
в котором разложение начинается с частоты следования w_к. В данном случае очевидно, что, раз выходной сигнал представляется суммой бесконечного ряда, то мы имеем дело с точечным спектром сигнала, поскольку он дискретен. Следовательно, любое периодическое колебание можно рассматривать как сигнал с дискретным спектром, поскольку непрерывным спектром он не обладает. Однако, если же взять непериодический сигнал, например, единичный прямоугольный импульс, то вводится понятия прямого и обратного преобразований Фурье:

 ,

где S(w) – спектральная плотность сигнала s(t).

Соответственно, S(w) – непрерывная по w функция, и в данном.

Заключение

В работе не ставилась цель охватить весь курс спектральной теории и спектрвльных характеристик, а ставилась цель изучить основные спектральные характеристики линейных операторов, и обрисовать применение этих понятий. Опять же, класс Фурье преобразований включает в себя намного больший объем, чем тот, о котором упомянуто в работе, они используются в теории алгоритмов при кодировке и сжатии информации в цифровом формате изображений JPEG, в вейвлет - преобразованиях. Новое поколение функциональной электроники содержит на элементарном уровне элементы, способные производить непрерывные преобразования Фурье и Лапласа, что намного ускоряет работу электронных устройств.

В общем и целом, наряду с первой частью работа дает представление о б основных спектральных характеристиках линейных операторов и их применении в различных областях математики, информатики и физики.

Список литературы

 

1.   Лекции по математической физике, Попов И.Ю., СПбГУ ИТМО, кафедра высшей математики.

2.   Элементы теории функций и функционального анализа, А.Н. Колмогоров и С.В. Фомин.

3.   Теория цепей и сигналов, Новиков Ю.Н.

4.   Свободная энциклопедия Википедия.

5.   Сжатие данных, изображения и звука, Д. Сэломон.