 | |||
Великий древнегреческий ученый родился на острове Самос в VI веке до н.э. В молодости побывал в Египте, где учился у жрецов. Говорят, что он был допущен в сокровенные святилища Египта, посетил халдейских мудрецов и персидских магов. Около 530 г. до н.э. Пифагор переехал в Кротон – греческую колонию в Южной Италии, где основал так называемый пифагорейский союз (или кротонское братство). В сферу интересов членов союза входили научные исследования, религиозно-философские искания, политическая деятельность. Они вели суровый образ жизни, превыше всего ценили самообладание, смелость и коллективную дисциплину. Пифагорейцы жили вместе, у них было совместное имущество, и даже свои открытия они считали общим достоянием. Деятельность союза была окружена тайной, поэтому никаких текстов от ранних пифагорейцев не осталось. Кроме того, по традиции, они все открытия приписывали Пифагору, о котором уже при жизни ходили легенды. Кто на самом деле является автором того или иного результата, неизвестно.
Пифагорейцы называли свои собственные исследования «математа», что означает «науки», и делили их на четыре части: арифметику, геометрию, астрономию и гармонию (т.е. учение о музыке). Главной считалась арифметика. Именно она лежала в основе и геометрии, и астрономии, и гармонии.
Пифагорейцы представляли числа как совокупность точек, образующих геометрические конфигурации – наподобие рисунка из камешков на земле. Таким образом, под числом они подразумевали «множество единиц» и признавали только целые положительные числа, разделяя их на четные и нечетные. Пифагорейцы доказали первую теорему теории делимости: произведение двух чисел четно тогда и только тогда, когда четно по крайней мере одно из них. Они также поставили задачу о нахождении совершенных чисел, т.е. чисел, равных сумме своих делителей. Единица считалась неделимой, у нее не было «долей». Вместо этого пифагорейцы рассматривали отношения (т.е. пропорции) целых чисел. К примеру, они могли сказать, что 2 точно так относится к 3, как 4 к 6. Говоря современным языком, они построили теорию рациональных чисел как теорию пар.
Остается неизвестным, сколько и какие именно аксиомы положили ранние пифагорейцы в основу своей геометрии, но все они относились к планиметрии прямолинейных фигур. Изучались свойства треугольников, прямоугольников, параллелограммов и других плоских фигур, сравнивались их площади. Венчало их систему знаний доказательство знаменитой теоремы Пифагора, которая была известна до этого как лишь как факт для некоторых частных случаев. Трудно переоценить значение теоремы Пифагора. Её обобщение и сегодня лежит в основе всех метрических пространств.
Можно утверждать, что и в стереометрии пифагорейцы достигли больших успехов. По свидетельству греческого историка и философа Прокла, именно они построили 5 правильных многогранников: тетраэдр, куб, октаэдр, додекаэдр и икосаэдр. Правда, многие современные исследователи считают, что Пифагору были известны лишь куб, тетраэдр и додекаэдр, а октаэдр и икосаэдр открыл Теэтет Афинский, талантливый ученик пифагорейца Феодора Керенского и Платона.
Пифагорейцы считали, что Земля имеет форму шара и находится в центре вселенной: ведь нет никаких оснований, что она была смещена или вытянута в какую-то одну сторону. Солнце же, Луна и пять планет (Меркурий, Венера, Марс, Юпитер и Сатурн) движутся вокруг Земли. Расстояния от них до нашей планеты таковы, что они как бы составляют семиструнную арфу, и при их движении возникает прекрасная музыка – музыка сфер. Обычно люди не слышат её из-за суеты жизни, и лишь после смерти некоторые из них смогут насладиться ею. А Пифагор слышал её при жизни. Строй арфы должен был подчиняться законам арифметики. В частности, как обнаружили пифагорейцы, такие музыкальные интервалы как октава, квинта и кварта, соответствуют звучанию пары одинаково натянутых струн, длины которых находятся в соотношении 1/2, 2/3 и 3/4.
Все эти открытия привели пифагорейцев к идее, что «все есть число», т.е. законы природы не что иное, как законы целых чисел и их отношений.
Похожие работы
... и другими науками. Часто занятия проводились на открытом воздухе, в форме бесед. Среди первых учеников школы было и несколько женщин, включая и Теано – жену Пифагора. С самого начала в пифагоризме сформировались два различных направления – "асуматики" и "математики". Первое направление занималось этическими и политическими вопросами, воспитанием и обучением, второе – главным образом ...
... оставило свой отпечаток в сознании Пифагора. Как бы то ни было, но пора ученичества подходила к концу. Возможно, неудовлетворенность бездоказательностью египетской математики ускорила окончательное решение Пифагора возвращаться на родину. Нужно было ехать домой и создавать свою школу. Но нелегко было теперь осуществить это, решение, обратное тому, что привело Пифагора 11 лет назад в Египет. ...
... почиталось. После смерти Пифагора его школа постепенно распалась, но те, кто был облагодетельствован его учением, хранили память о великом философе так же, как они во время жизни почитали человека. Прошло время , и Пифагор стал считаться уже не человеком, а богом, и его рассеянные по свету ученики были объединены общим восхищением все превосходящим гением своего учителя. Эдуард Шуре в своей ...
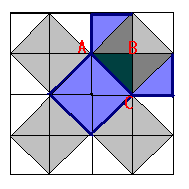
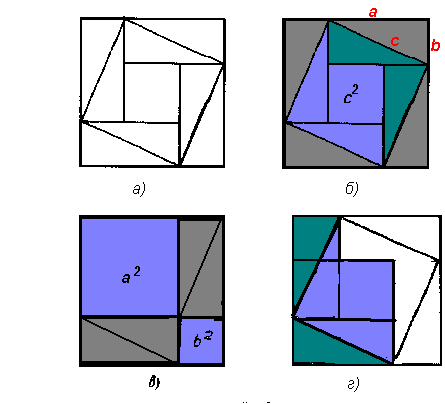
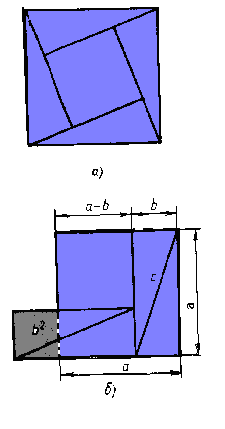
... г), то легко обнаружить, что полученная фигура, которую иногда называют “креслом невесты”, состоит из двух квадратов со сторонами а и b, т.е. с2=а2+Ь2. На рисунке 3 воспроизведен чертеж из трактата “Чжоу-би...”. Здесь теорема Пифагора рассмотрена для египетского треугольника с катетами 3, 4 и гипотенузой 5 единиц измерения. Квадрат на гипотенузе содержит 25 клеток, а вписанный в него квадрат на ...



0 комментариев