Волновая теория фотона

Волновая теория фотона

Если взять несколько шестигранников разных размеров и разместить их на наклонной плоскости, то все они будут скатываться вниз с одной и той же постоянной скоростью , но с разной частотой (табл. 1).

Таблица 1. Кинематические параметры движения тел.

Форма тел	, м	t, с	V, м/с
Цилиндрические	0,008 0,010 0,0!3	2,43 2,30 2,05	0,83 0,89 0,99	- - -
Шестигранные	0,0065 0,0080 0,0130	5,68 5,67 5,67	0,18 0,18 0,18	27,69 22,50 13,85

Обратим внимание на то, что при увеличении радиуса  шестигранника частота  его движения уменьшается так же, как и у фотона. Конечно, у фотона нет плоскости, по которой он мог бы перемещаться, как тела, представленные в табл. 1. Однако центр масс электромагнитной модели фотона описывает укороченную циклоиду, осью симметрии которой является прямолинейная ось ОХ, лежащая в плоскости его поляризации.

Начнем с вывода уравнений движения центра масс  фотона. Поскольку центр масс фотона движется в плоскости поляризации и в рамках аксиомы Единства пространства – материи – времени, то для описания его движения по волновой траектории необходимо иметь два параметрических уравнения.

Так как центр масс  фотона движется относительно наблюдателя и относительно геометрического центра , который движется прямолинейно со скоростью , то для полного описания такого движения необходимо иметь две системы отсчета: неподвижную  и подвижную .

Амплитуда  колебаний центра масс  фотона будет равна радиусу  его вращения относительно геометрического центра  фотона:

.

Обратим внимание на небольшую величину амплитуды  колебаний центра масс фотона в долях длины его волны или радиуса вращения.

Уравнения движения центра масс  фотона относительно подвижной системы  имеют вид параметрических уравнений окружности :

 ;

.

Если фотон движется относительно неподвижной системы отсчета ХОУ со скоростью , то уравнения такого движения становятся уравнениями циклоиды:

 ;

.

Обратим внимание на то, что в уравнениях  и . Это значит, что они описывают движение центра масс фотона по волновой траектории в рамках аксиомы Единства пространства – материи – времени. Отметим, что уравнения Луи Де Бройля и Шредингера этим свойством не обладают. Учитывая соотношения, получим:

где  .

Представим траектории точек . Обратим внимание на важные особенности. Радиус кольца равен  и точка , лежащая на кольце, описывает обыкновенную циклоиду М.

Радиус окружности, описываемой точкой , -  и эта точка описывает удлинённую циклоиду (рис. 1).

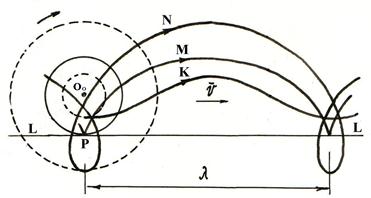
Рис. 1. Траектории движения точек , представленных на рис. 15:

М – обыкновенная циклоида; N – удлинённая циклоида; К – укороченная циклоида;

Радиус окружности, описываемой точкой  (рис. 1), , и она описывает укороченную циклоиду .

Так как у модели фотона амплитуда , то его центр масс движется по укороченной циклоиде.

Результаты табл. 1 требуют, чтобы математическая модель, описывающая скорость центра масс шестигранника, а значит и фотона, не зависела бы от его радиуса  вращения. Уравнения автоматически дают такой результат

Если считать, что движение фотона эквивалентно движению шестигранника, то  и получаем закономерность изменения скорости центра масс фотона, в которую легко вводятся электрическая  и магнитная  постоянные

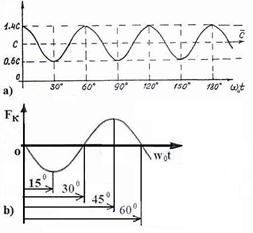
График скорости центра масс фотона показан на рис. 2, а.

Как видно, скорость центра масс  фотона действительно изменяется в интервале длины волны или периода колебаний таким образом, что её средняя величина остается постоянной и равной .

Поскольку сила инерции направлена противоположно ускорению, то касательная составляющая силы инерции , действующая на центр масс фотона, запишется так

.

Несмотря на сложность переменной составляющей математической модели (108), касательная сила инерции, действующая на центр масс фотона, изменяется синусоидально (рис 2, b). Это значит, что она генерирует прямолинейное движение фотона так же, как и сила инерции, движущая автомобиль (рис. 2, b) или силы инерции дисбалансов, вращающие потребителя механической энергии электромотора, о которых мы подробно расскажем в ответах на вопросы.

Рис. 2. а) - график скорости центра масс фотона; b) - зависимость изменения силы инерции, действующей на центр масс светового фотона в интервале одного колебания

Уравнения движения центра масс  одного из электромагнитных полей фотона относительно подвижной системы отсчета  будут иметь вид:

;

 .

Уравнения абсолютного движения центра масс одного электромагнитного поля фотона, то есть движение относительно неподвижной системы отсчета  принимают вид:

;

 .

Это – уравнения волнистой циклоиды. Они позволяют легко определить все кинематические характеристики центров масс электромагнитных полей фотона.

Итак, мы получили уравнения, которые точнее уравнения Луи Де Бройля и уравнения Шредингера описывают движение фотона. Однако, если появляются более точные математические соотношения для описания поведения какого-либо объекта, то менее точные обязательно должны содержаться в них и быть их следствиями. Этому требованию полностью отвечают соотношения, описывающие движение центра масс фотона.

Чтобы получить волновое уравнение Луи Де Бройля, надо вывести процесс описания движения центра масс фотона за рамки аксиомы Единства пространства - материи - времени. Для этого надо взять одно из уравнений, например, уравнение. Обращаем внимание читателя на то, что эта операция автоматически выводит процесс описания движения центра масс фотона за рамки аксиомы Единства пространства - материи - времени.

Чтобы привести это уравнение к виду, необходимо ввести в него координату , используя для этого разность фаз.

.

Учитывая, что  и , имеем

.

Обозначим:

 

тогда

Нетрудно показать, что уравнение Луи – Де Бройля легко приводится к уравнению Шредингера. Для этого выразим из формул (86) и (92) частоту  и длину волны .

 ,

Введем новое обозначение функции и подставим в неё значения.

 .

При фиксированном  смещение  является гармонической функцией времени, а при фиксированном  - координаты . Обратим внимание на то, что эти представления находятся за рамками аксиомы Единства.

Дифференцируя уравнение дважды по , найдем

.

Если с помощью соотношения описывать поведение электрона в атоме, то надо учесть, что его кинетическая энергия  и импульс  связаны соотношением

.

Откуда

.

Подставляя результат в уравнение, имеем

Известно, что полная энергия электрона  равна сумме кинетической  и потенциальной  энергий, то есть

 .

С учетом этого уравнение принимает вид дифференциального уравнения Э. Шредингера.

Из изложенного следует, что результат решения уравнения есть функция, работающая за рамками Аксиомы Единства пространства – материи – времени.

Если в функции разделить переменные  и , то можно получить уравнение

,

которое работает в рамках аксиомы Единства, поэтому оно должно давать точный результат, соответствующий эксперименту. И это действительно так. Оно рассчитывает спектр атома водорода. Происходит это потому, что энергии связи электрона с протоном зависят только от расстояния между протоном и электроном и не зависят от времени.

Таким образом, мы вывели постулированные раннее математические модели квантовой механики, описывающие поведение фотона. Мы показали, что уравнение Луи Де Бройля и трехмерное уравнение Шредингера работают за рамками аксиомы Единства пространства - материи – времени.

Далее, при анализе других физических явлений, в которых явно проявляется поведение фотонов, мы получим аналитически остальные и многие другие, в том числе и новые математические модели.

Итак, мы оставляем в покое почти все математические формулы, которые давно применяют для описания поведения фотона. В этом смысле у нас нет ничего нового, мы только подтвердили достоверность этих формул и дополнили их уравнениями, описывающими движение центра масс фотона в рамках аксиомы Единства пространства – материи – времени.

Поскольку основные математические модели, описывающие главные характеристики фотона, выведены аналитически из анализа движения его модели, то это является веским основанием для использования этой модели при интерпретации результатов всех экспериментов, в которых участвуют фотоны. Количество таких экспериментов неисчислимо, поэтому мы будем рассматривать лишь те из них, которые носят обобщающий характер. Самая большая совокупность экспериментальных данных, в которых зафиксировано поведение фотонов – шкала электромагнитных излучений, представленная в таблицах 1.

Мы будем обращаться к этим таблицам при интерпретации почти всей совокупности экспериментов с участием фотонов, а сейчас определим лишь интервал изменения длины волны фотонов.

Длина волны электромагнитного излучения изменяется в интервале  (табл. 1). Минимальная величина этого интервала принадлежит гамма-фотону, а максимальная - низкочастотному диапазону излучения. Величины эти установлены экспериментально и у нас нет оснований сомневаться в их достоверности. Но, как мы уже отметили, у нас есть основания сомневаться в том, что самый большой фотон имеет длину волны .

Материальная плотность базового кольца  фотона, соответствующего минимальной длине волны , равна

.

Материальная плотность базового кольца фотона, соответствующего максимальной длине волны электромагнитного излучения , равна

Теперь ясно, что максимальную проницаемость гамма фотона обеспечивает его минимальный размер (радиус ) и максимальная масса . Что же касается фотона с максимальной длиной волны  и минимальной массой , то тут - полная неясность. Трудно представить фотон с базовым радиусом , движущийся со скоростью света, имея материальную плотность кольца

Вряд ли возможно формирование ньютоновских и электромагнитных сил при такой небольшой материальной плотности базового кольца фотона. Поэтому должен существовать предел максимальной длины волны  или максимального радиуса и минимальной массы  фотона.

Дальше мы проведём детальное обоснование , а сейчас отметим ещё раз, поскольку тепловую энергию и температуру формируют фотоны, то соответствует самой низкой температуре, существующей в Природе, экспериментальное значение которой равно, примерно, . Длина волны совокупности фотонов, формирующих эту температуру, определяется по формуле Вина.

,

где - постоянная Вина, четвёртая константа, контролирующая поведение фотонов.

Фотоны с такой длиной волны соответствуют реликтовому диапазону Их масса равна

.

Плотность материального кольца такого фотона будет равна

или

Таким образом, в Природе нет фотонов с длиной волны или радиусом вращения, большим 0,052м. Конечно, эта величина будет ещё уточняться, но в любом случае она будет иметь значения, близкие к 0,052м.

Итак, фотонная шкала электромагнитных излучений начинается с реликтового диапазона. Минимальную энергию , минимальную массу  и минимальную частоту , но максимальную длину волны  (или радиус  вращения) имеет инфракрасный фотон в реликтовом диапазоне:

;

;

Максимальную энергию , максимальную массу  и максимальную частоту , но минимальную длину волны  (или радиус ), имеет гамма-фотон:

 ;

;

Как видно, самый маленький фотон - гамма-фотон, а самый большой фотон - инфракрасный фотон реликтового диапазона.

Таким образом, максимальная длина волны единичных фотонов соответствует реликтовому диапазону, а минимальная - гамма диапазону. От реликтового диапазона до гамма диапазона длина волны фотона уменьшается, примерно, на 15 порядков, а частота увеличивается настолько же.