В’язка взаємодія вихорових структур зі зсувною течією

НАЦІОНАЛЬНА АКАДЕМІЯ НАУК УКРАЇНИ

ІНСТИТУТ ГІДРОМЕХАНІКИ

РОЗУМНЮК Наталія В’ячеславівна

УДК 532.526

В’язка взаємодія вихорових структур

зі зсувною течією

01.02.05 - механіка рідини, газу та плазми

Автореферат

дисертації на здобуття наукового ступеня

кандидата фізико-математичних наук

Київ - 2003

Дисертацією є рукопис.

Робота виконана в Інституті гідромеханіки (ІГМ).

Національної Академії наук України.

Науковий керівник доктор фізико-математичних наук:

Воропаєв Геннадій Олександрович,

Інститут гідромеханіки НАН України, завідувач відділу гідробіоніки та керування пограничним шаром.

Офіційні опоненти доктор фізико-математичних наук, професор Приходько Олександр Анатолійович,

Дніпропетровський державний університет, завідувач кафедри технічної механіки кандидат фізико-математичних наук, старший науковий співробітник Горбань Володимир Олексійович.

Інститут гідромеханіки НАН України, старший науковий співробітник

Провідна установа Національний університет імені Тараса Шевченка (м. Київ)

Захист відбудеться „11" грудня 2003р. о 14 годині на засіданні спеціалізованої ради Д 26.196.01 в Інституті гідромеханіки НАН України за адресою:

03057, Київ, вул. Жедябова 8/4

З дисертацією можна ознайомитись у науковій бібліотеці

Інституту гідромеханіки НАН України

Автореферат розісланий „7” листопада 2003р.

Вчений секретар

спеціалізованої вченої ради

д. т. н., професор Криль С.І.

ЗАГАЛЬНА ХАРАКТЕРИСТИКА РОБОТИ

 

Актуальність теми. Сучасний етап розвитку техніки та технологій потребує все більш докладних знань про складні нестаціонарні процеси, які відбуваються в рідинах, оскільки це дозволяє покращувати експлуатаційні характеристики машин та механізмів, підвищувати ефективність роботи, економити енергетичні ресурси.

В багатьох випадках гідродинамічні характеристики твердих тіл при обтіканні їх потоком в’язкої рідини визначаються параметрами пограничного шару, що утворюється на поверхні тіл. Додаткові ускладнення виникають при взаємодії пограничного шару зі збуреннями, які або вже існують в набігаючому потоку, або розвиваються внаслідок неоднорідності геометричної форми поверхні. Такі процеси є суттєво нестаціонарними, тобто основні характеристики потоку можуть зазнавати значних змін у часі, що відповідно впливає на гідродинамічні характеристики тіл.

Щоб вивчити тонкі фізичні процеси в таких течіях, потрібно мати дані не тільки про інтегральні параметри тіла в потоці та поведінку потоку в деяких місцях, а й про структуру потоку в цілому і її зміни в часі. Експериментальні дослідження нестаціонарних течій, які б коректно вивчали ці явища з достатньою точністю, є дуже складними і витратними, а теоретичний аналіз рівнянь, що їх описують, стикається зі значними математичними ускладненнями.

Тому чисельний експеримент по вивченню нестаціонарної взаємодії пограничного шару з інтенсивними збуреннями потоку та їх впливу на гідродинамічні характеристики тіл набуває важливого значення.

Багато існуючих методів чисельного аналізу течій в’язкої рідини побудовані на основі тих чи інших спрощень математичної моделі, які коректно описують поведінку потоку в певному діапазоні зміни параметрів або для певних масштабів фізичних явищ. На відміну від цього, повні нестаціонарні рівняння Нав’є-Стокса дають змогу досліджувати процеси, що відбуваються в усіх областях в’язкої течії, включаючи і пограничний шар біля поверхні тіла, і потік далеко за межами пограничного шару.

Зв'язок роботи з науковими програмами, планами, темами. Дисертаційну роботу виконано у рамках держбюджетних тем “Вивчення взаємодії та керування різних когерентних вихрових структур в пристінних течіях ” 1998-2001г. г., шифр 1.3.7.12, “Розробка методів керування силами взаємодії між тілом та рідиною з використанням механізмів генерації когерентних структур в пристінних течіях ” 1999-2002г. г., шифр 1.10 1.5

Мета і задачі дослідження. Мета дисертації полягає у виявленні основних механізмів та закономірностей при взаємодії вихорових збурень, які містяться в набігаючому потоку, з пограничним шаром на поверхні твердого тіла, а також у дослідженні структури потоку та розвитку збурень у пограничному шарі при наявності крупномасштабної геометричної неоднорідності обтічної поверхні.

Для цього розв’язуються такі задачі:

розробка алгоритму та створення комплексу програм для чисельного аналізу нестаціонарного потоку в’язкої нестисливої рідини в присутності твердих границь;

дослідження взаємодії тонкої скінченої пластини з системою вихорів, що набігають з потоком рідини;

вивчення характеристик обтікання пластини при відсмоктуванні частини рідини з пограничного шару на її поверхні через відвідний канал, розташований під кутом до пластини;

виявлення структури течії на поверхні з однією або кількома послідовними виїмками різної форми в різних режимах обтікання;

вивчення впливу зміни структури течії в цих випадках на гідродинамічні параметри тіла.

Об’єктом дослідження є потік в’язкої нестисливої рідини поблизу твердої поверхні.

Предметом дослідження є структура течії і динамічні характеристики обтікання твердої поверхні при наявності неоднорідності границі або потоку.

Метод дослідження - чисельний аналіз нестаціонарних рівнянь Нав’є-Стокса, записаних у змінних завихреність - функція течії, при відповідних граничних та початкових умовах, що моделюють обтікання твердої поверхні потоком в’язкої нестисливої рідини та вільний потік вдалині від поверхні. Рівняння розв’язуються cкінченорізницевими методами.

Наукова новизна роботи. Вперше на основі розв’язку повних рівнянь Нав’є-Стокса проаналізовано процес взаємодії детермінованих вихорових збурень у потоку з гострою кромкою і пограничним шаром на скінченій пластині. Проведено аналіз процесу руйнування вихору при прямому ударі з кромкою і подальшого впливу на пограничний шар в залежності від початкових параметрів вихору.

Показано суттєву відмінність картини взаємодії з гострою кромкою у випадках одиночного вихору і пари вихорів, а також залежність від взаємного розташування вихорів і пластини.

Виявлено умови існування безвідривного обтікання при відсмоктуванні рідини з пограничного шару на пластині через відвідний канал, розташований під кутом до пластини.

Проведено аналіз обтікання потоком в’язкої рідини поверхні з геометричною неоднорідністю у вигляді однієї або системи виїмок різної форми та розміру. Підтверджено існування як стаціонарного, так і квазіперіодичного режиму обтікання.

Достовірність отриманих результатів забезпечено використанням для чисельного моделювання повних рівнянь Нав’є-Стокса та коректних методів їх розв’язку, якісною та кількісною відповідністю чисельних результатів експериментальним даним.

Практичне значення одержаних результатів. Виконані теоретичні дослідження дозволяють краще зрозуміти механізми процесів, які відбуваються при взаємодії потоку в‘язкої рідини з твердими тілами в присутності вихорових збурень, що містяться у набігаючому потоку або викликаних формою поверхні тіла. Це дає змогу цілеспрямовано впливати на структуру потоку в різних режимах, які залежать як від параметрів потоку, так і геометрії поверхні, і таким чином керувати гідродинамічними характеристиками тіл.

Особистий внесок здобувача. Вибір загального напрямку досліджень та постановка окремих задач належать науковому керівникові - доктору фіз. - мат. наук Г.О. Воропаєву. Розробка алгоритмів, створення програм, чисельний розв’язок та попередній аналіз результатів виконані дисертантом особисто.

Апробація результатів дисертації. Основні положення й результати дисертації доповідалися на III Республіканській школі-семінарі молодих вчених та спеціалістів по теоретичній та прикладній гідродинаміці (м. Алушта, 1988р), міжнародній конференції EUROMECH Colloquium 327 (м. Київ, 1994р), 2 Сибирському семінарі зі сталості гомогенних и гетерогенних рідин (м. Новосибірськ, 1995р), міжнародній конференції 11^th European Drag Reduction Working Meeting (м. Прага, Чехія, 1999р), міжнародній конференції "Organized vortical motion as a basis for boundary-layer control" (м. Київ, 2000р), міжнародній конференції “Актуальні проблеми механіки суцільних середовищ" (м. Донецьк, 2002р), семінарі Інституту гідромеханіки НАН України (м. Київ, 2003р), міжнародній конференції „Сучасні проблеми механіки” (м. Київ, 2003р)

Публікації. Основні ідеї та положення дисертації викладено в 7 публікаціях, з них 3 - у фахових виданнях згідно з переліком ВАК України, 4 - у тезах конференцій.

Структура дисертації. Дисертація складається зі вступу, п’яти розділів, висновків, списку використаних джерел. Повний обсяг роботи складає 133 сторінок, в тому числі 66 рисунків, 1 таблиця, 9 сторінок займає список використаних джерел.

ОСНОВНИЙ ЗМІСТ РОБОТИ

У вступі обґрунтовується актуальність тематики досліджень, визначаються мета і задачі роботи, а також методи їх розв’язання, викладається наукова новизна та практичне значення одержаних результатів.

В першому розділі розглянуто стан вивчення явищ, пов’язаних з нестаціонарною взаємодією вихорових збурень в потоку в’язкої рідини з пограничним шаром на поверхні твердих тіл, а також з обтіканням поверхні зі значною геометричною неоднорідністю (каверною) та відсмоктуванням частини рідини з пограничного шару через поверхню тіла.

В теоретичних роботах таких вчених, як H. C. Rogler, E. Reshotko, Г.О. Воропаєв, взаємодія вихорових структур з пограничним шаром досліджується у лінеаризованій постановці, що виходить з малості збурень і дозволяє розглядати реакцію пограничного шару на зовнішні збурення.

Інтенсивні вихорові утворення та їх вплив на течії поблизу твердої границі вивчалися рядом дослідників на основі моделі ідеальної рідини (С.М. Білоцерковський, А.С. Гіневський, В.О. і О.М. Горбань, Г.І. Таганов, A. G. Panaras,), що дає коректні результати у припущенні, що пограничний шар дуже тонкий і практично не впливає на структуру потоку. Деякі автори, як наприклад M. R. Maixner, J. - H. Park, D. - J. Lee, вводять в граничні умови прилипання поправку для врахування в’язкості.

Дослідження в рамках теорії пограничного шару (J. K. Harvey, F. J. Perry, T. L. Doligalski, J. D. A. Walker, A. T. Conlisk) коректно описують параметри потоку до моменту відриву потоку від поверхні.

В той же час, експериментальні дослідження (D. Rockwell, B. D. Kothmann, W. R. Pauley, M. Macrorie, D. R. Poling, L. Dadone, D. P. Telionis, T. Shizawa, J. K. Eaton) показують, що крупномасштабні інтенсивні вихрі можуть повністю змінювати структуру пограничного шару, спричинювати місцевій відрив потоку і навіть повністю руйнувати пограничний шар. Для теоретичного аналізу таких складних течій необхідно розв’язувати повні рівняння Нав’є-Стокса.

Те ж саме є справедливим і для течій на твердій поверхні, яка має геометричні неоднорідності досить великого масштабу, тобто такі, які суттєво змінюють розподіл тиску біля поверхні. Експериментальні дані про потоки навколо виїмок, приведені в роботах багатьох авторів, в тому числі у книзі „Управление обтеканием тел с вихревыми ячейками в приложении к летательным аппаратам интегральной компоновки (численное и физическое моделирование)” (під ред. А.В. Єрмишина та С.О. Ісаєва), а також статтях С.О. Ісаєва, В.В. Бабенко, V. Sarohia, D. Rockwell, M. Gharib, A. Roshko, показують, що картина обтікання може суттєво змінюватися в залежності від розмірів виїмки та параметрів зовнішнього потоку. Режим течії може бути як стаціонарним, так і періодичним у часі. В останньому випадку виїмка має впливати на основний потік на досить великій відстані вниз за течією, суттєво змінюючи характеристики пограничного шару.

В той же час, в більшості робіт вивчається потік у власне виїмці, або її безпосередньому околі. Для оцінки впливу присутності виїмок на обтікання поверхні необхідно вивчати поведінку потоку в цілому, включаючи як область навколо виїмки, так і потік за її межами, використовуючи рівняння Нав’є-Стокса.

У другому розділі описується фізична та математична модель для вивчення поведінки потоку в’язкої рідини в присутності твердих границь та інтенсивних великомасштабних збурень, які можуть суттєво впливати на основні характеристики потоку та обтічної поверхні. Описуються основні характеристики чисельних методів для розв’язання основної системи рівнянь та вимоги до розрахункових схем. Обґрунтовується вибір неявної схеми змінних напрямків для чисельного аналізу сформульованої задачі.

Основні рівняння - це нестаціонарні рівняння Нав’є-Стокса, перетворені у плоскому випадку до змінних завихреність - функція течії та знерозмірені відносно швидкості вільного потоку та характерного лінійного масштабу:

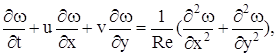 (1)

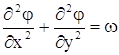, (2)

де функція течії j та завихреність w визначаються наступним чином:

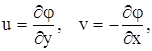
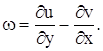
На границях розрахункової області накладено наступні граничні умови: на вході до області задано незбурений потік, на виході - м’які граничні умови, на границі, що знаходиться у вільному потоку, задано умови “рухомої кришки без тертя", на твердій поверхні - умови прилипання.

В області побудовано прямокутну сітку з вузлами, розміщеними нерівномірно в обох напрямках таким чином, що розрахункові точки згущуються біля поверхні пластини та її кінців.

При дискретизації рівнянь похідні 2-го порядку апроксимуються різницями 2-го порядку, для конвективних членів у рівнянні (1) застосовано направлені різниці як 1-го, так і 3-го порядку. Останні використано у випадку більш високих чисел Рейнольдса та суттєво нестаціонарної поведінки потоку.

Граничні умови прилипання на твердій поверхні задано як:

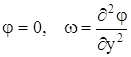. (3)

 

Для запису чисельного аналога другої формули використано як формулу Тома по двом точкам, так і формулу Йенсена по трьом точкам, а також їх комбінацію.

Побудований алгоритм дозволяє досліджувати нестаціонарні течії, або одержувати стаціонарний режим методом усталення як граничний розв’язок.

У третьому розділі побудований алгоритм використано для розв’язку задачі про стаціонарне обтікання пластини, яка знаходиться в потоку в‘язкої рідини паралельно до напрямку основного потоку, при різних значеннях числа Рейнольдса по довжині пластини від 10² до 10⁵. Показано відповідність одержаних результатів даним експериментальних досліджень, а також теоретичного та чисельного аналізу інших авторів. Одержані результати далі використовуються як початкові умови для розв’язку нестаціонарних задач.

Розв’язано також задачу про обтікання пластини з відсмоктуванням рідини через відвідний канал, розташований під різними кутами до пластини, при числах Рейнольдса по довжині пластини 100¸500. Пластина знаходиться на нижній границі розрахункової області. На частині границі перед пластиною та позаду її задано граничні умови симетрії потоку: j=0, w=0.

При чисельному дослідженні одержано стаціонарний режим обтікання. Показано, що в залежності від кута нахилу каналу, інтенсивності відсмоктування, числа Рейнольдса можуть формуватися дві відривні зони - біля нижньої за потоком кромки каналу в основному потоку вище поверхні пластини, і в каналі біля верхньої кромки. Таким чином, структура потоку і параметри пограничного шару в районі каналу суттєво відрізняються від тих, що виникають при моделюванні відмотування через скінчену щілину за допомогою пористої поверхні. Умови існування цих зон при фіксованих двох параметрах і змінному третьому не перетинаються, тобто існує можливість підібрати такі значення параметрів, щоб виключити, або мінімізувати обидві зони.

Четвертий розділ присвячено вивченню взаємодії скінченої пластини з вихорами, що набігають з потоком рідини при Re_L=10³¸10⁴. Вивчається так звана паралельна взаємодія, тобто така, коли вісь вихору направлено паралельно до розмаху тіла (пластини). Пластина знаходиться всередині розрахункової області.

Розглянуто декілька способів введення початкового вихору в розрахункову область. Як результат аналізу поведінки різних типів початкових вихорів для подальшого вивчення вибрано формулу так званого вихору Ламба:

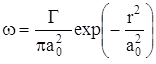. (4)

В початковий момент один або пара вихорів, описуваних формулою (4), накладаються на деякій відстані вгору за потоком від пластини на дані стаціонарного обтікання пластини, одержані при даному числі Рейнольдса за описаним чисельним алгоритмом методом усталення. Подальший розвиток потоку і зміни, які відбуваються з вихорами та пограничним шаром на пластині залежать від початкового діаметра вихору а₀, циркуляції Г, положення відносно пластини (початкового зсуву центру по вертикалі).

Процес взаємодії у часі можна розділити на три етапи (Рис.1). На першому етапі початковий вихор, який далі називається конвективним, знаходиться відносно далеко від пластини, його вплив проявляється у виникненні деякої асиметрії течії в районі передньої кромки пластини за рахунок створеного периферією вихору скосу потоку.

На другому етапі ядро вихору проходить поблизу носика пластини. Його початково кругла форма деформується, центр вихору зміщується по вертикалі. Відбувається прискорене зменшення максимальної завихреності в центрі вихору. На пластині може виникати перетікання частини рідини з однієї поверхні до іншої навколо передньої кромки. Це спричинює відрив на цій другій поверхні, з якого формується вихор з протилежним знаком завихреності відносно конвективного вихору. Конвективний вихор розрізається пластиною на дві частини.

На третьому етапі вихор або дві його частини мігрують вздовж різних боків пластини. Їх вплив на місцевий пограничний шар залежить від напрямку і величини поздовжньої компоненти швидкості в тому місці, де вони торкаються пограничного шару (Рис.2). Якщо напрямок співпадає з напрямком течії в пограничному шарі, градієнт швидкості по нормалі до поверхні збільшується, відповідно зростає місцеве тертя на пластині, і навпаки. Від цього ж залежить і швидкість, з якою частини вихору пересуваються вздовж пограничного шару. Тому вони неодночасно сходять з задньої кромки пластини. Вторинний вихор, який зійшов з передньої кромки і також мігрує в пограничному шарі, але з меншою швидкістю, зменшує градієнт швидкості і тертя на поверхні.

Вплив вихору на пограничний шар відображено у зміні з часом інтегрального коефіцієнта тертя пластини (Рис.3). Найбільші зміни відбуваються в тих випадках, коли центр вихору знаходиться на рівні передньої кромки під час другого етапу взаємодії. Зсув початкового положення центра по вертикалі до одного початкового діаметра вгору або вниз викликає не однакові зміни у процесі взаємодії внаслідок різних знаків завихреності у пограничному шарі на різних боках пластини.

Максимальні відхилення виникають на другому етапі, коли наближення будь-якого вихору викликає зменшення тертя за рахунок скошеного потоку навколо передньої кромки.

Зменшення циркуляції при однаковому початковому діаметрі зменшує інтенсивність взаємодії. При збільшенні циркуляції до Г=0.5 відривний вихор стає значно інтенсивнішим, після сходу з передньої кромки його дія на пограничний шар переважає вплив конвективного вихору, який зазнає посиленої дифузії.

При зменшеному числі Рейнольдса Re_L=10³ вплив проходження вихору значно ослаблюється, помітні зміни в пограничному шарі спостерігаються тільки в момент безпосереднього контакту ядра вихору з передньою кромкою. Відривний вихор не утворюється, а дві частини конвективного вихору виштовхуються на периферію пограничного шару і майже не викликають змін на поверхні пластини.

Результати розрахунків при більшому Рейнольдса Re_L=10⁵ показали сильну нестійкість пограничного шару на пластині до зовнішніх збурень. Наближення конвективного вихору викликає утворення і сходження послідовності інтенсивних відривних вихрів біля носика пластини, які продовжують розвиватися і взаємодіяти по мірі пересування за потоком вздовж пластини, і повністю руйнують пограничний шар.

Для пари вихорів однакового початкового діаметра і рівної за модулем, але протилежного знаку циркуляції Г, з’являється додаткова залежність від взаємного розташування вихорів, тобто відстані між центрами по вертикалі і горизонталі. Два вихори, розташовані симетрично відносно пластини, зберігають симетричність потоку на протязі всього часу. Швидкість їх руху як пари і вплив на пограничний шар на другому етапі залежать від напрямку індукованої швидкості на стику вихорів (Рис.4). Під час проходження повз передню кромку кожний з них зберігається як ціле. Тому, потрапляючи до пограничного шару, вони викликають більші ефекти, ніж одиночний вихор з такими ж початковими параметрами. Вплив на тертя на поверхні виявляє ті ж самі закономірності, як і для одиночного вихору під час третього етапу.

Два вихори, в яких центри мали зсув по горизонталі, індукують між собою вектор швидкості, який зсуває пару по вертикалі. Тому один з вихорів може проходити над передньою кромкою майже неушкодженим, а інший зазнає руйнування подібно до випадку одиночного вихору. Вплив на пограничний шар складається з незначної за величиною реакції на проходження першого вихору і набагато інтенсивнішого ефекту вихору, що руйнується.

П’ятий розділ розглядає обтікання пластини з однією виїмкою або системою виїмок в її поверхні. Пластина знаходиться на нижній границі розрахункової області.

У виїмці будується прямокутна розрахункова сітка таким чином, що її вузли знаходяться на стінках виїмки. За початкові умови взято обтікання гладенької пластини, у виїмці в початковий момент всі величини дорівнюють нулю. Кількість вузлів змінювалась для різних розмірів виїмок та режимів потоку, найбільша кількість досягала 110 по глибині і 210 по ширині.

В залежності від параметрів основного потоку та співвідношення геометричних розмірів виїмки та характерних товщин пограничного шару вивчено структуру потоку у виїмці та її вплив на основний потік. При малих та помірних значеннях місцевого числа Рейнольдса (Re_x<10⁴) і відносно невеликій ширині виїмок (d/b>0.2, де d - товщина пограничного шару перед виїмкою, b - ширина виїмки) обтікання має стаціонарний характер. У виїмці формується циркуляційний потік малої інтенсивності навколо одного центра (Рис.5), він відділений від основного потоку нульовою лінією току, через яку не відбувається обміну рідиною між цими зонами потоку.

На верхній границі виїмки відбувається зниження місцевого тертя за рахунок зменшення градієнта швидкості, але на її кромках концентруються зони підвищеної завихреності, як у випадку гострих кромок, так і у випадку заокруглених (Рис.6). Ефект присутності виїмок має локальний характер, обтікання пластини з виїмками в цілому майже не відрізняється від обтікання гладенької пластини.

Досліджено також вплив на структуру течії дискретного відсмоктування/вдуву однакової інтенсивності, яке здійснюється через стінки виїмок на різній відстані від дна. Показано, що локальне зниження градієнта швидкості на ширині виїмки поблизу її верхньої границі компенсується підвищенням завихреності біля вершин виїмок.

При підвищенні числа Рейнольдса і тоншому пограничному шарі у виїмці утворюється складна структура потоку з декількома вихоровими зонами, де рідина має завихреність протилежних знаків. При Re_b=15625 біля вихідної кромки знаходиться інтенсивний вихор, в решті об’єму виїмки швидкість значно менша (Рис.7). Вздовж ширини виїмки відбувається розвиток нестійкості зсувного шару, який утворюється з пограничного шару, що сходить з передньої кромки. Це спричинює коливання потоку, які інтенсифікуються при взаємодії зсувного шару з вихідною кромкою, що, в свою чергу, призводить до коливань в пограничному шарі вниз за течією від виїмки (Рис.8).

Коливання біля передньої кромки мають таку ж частоту і узгоджені за фазою з вихідною кромкою, але значно менші за амплітудою.

При Re_b=31250 інтенсивні вихорові утворення займають практично всю виїмку (Рис.9). Їх взаємодія між собою та зі зсувним шаром призводить до більш складного характеру коливань (Рис.10), коли відбувається нерегулярна зміна частоти та амплітуди. Крім того, спостерігається втрата фазової узгодженості коливань біля вхідної та вихідної кромок. Збурення основного потоку над виїмкою та нижче за течією є настільки інтенсивними, що повністю змінюють структуру пограничного шару.

Встановлення стаціонарного або квазіперіодичного режиму обтікання відповідає експериментальним результатам, а також деяким теоретичним дослідженням різних авторів для подібних, але не однакових з даними, геометричних форм виїмок. Визначальними параметрами для того чи іншого режиму являються як параметри пограничного шару перед виїмкою, так і співвідношення характерних лінійних масштабів місцевого пограничного шару і геометричних розмірів виїмки. Так, D. Rockwell та інші використовують відношення товщини втрати імпульсу перед виїмкою d^** до її ширини b. V. Sarohia (1977, AIAA Journal, Vol.15, №7, P.984-991) використав за критерій появи коливань безрозмірний параметр bRe_d^1/2/d, який в його експериментах перевищує 300 при квазіперіодичному режимі.

В Табл.1 наведено ці та інші основні параметри, одержані в результаті чисельного дослідження обтікання напівциліндричної виїмки, які узгоджуються з експериментальними даними при різних режимах обтікання.

Набір параметрів у стовпчику I характеризує стаціонарний режим.

При значеннях параметрів, наведених у стовпчику II, коливання відбувалися на початковому етапі, коли рідина з зовнішнього потоку потрапляла у виїмку, далі ці коливання майже зникали. Цей випадок представляв собою перехідний стан між стаціонарним обтіканням виїмки та режимом зсувного шару.

При обтіканні виїмки потоком з параметрами, виписаними у стовпчику III, одержано стійкі коливання, частотні характеристики яких зберігаються в процесі подальшого розрахунку. При Re_b=15625 на ширині виїмки вміщується дві довжини хвилі збурень, у відповідності до D. Rockwell, A. Schachenmann (1981, J. of Fluid Mech., Vol.117, P.425-441). Існує одна частота коливань. Її безрозмірне значення дорівнює fd^**/U_¥»0.014, що відповідає частоті зсувного шару (Knisely C., Rockwell D. Self-Sustained Low-Frequency Components in an Impinging Shear Layer, 1982, Journal of Fluid Mechanics, Vol.116, P.157-186). Отже, при такому режимі основним фізичним механізмом, що відповідає за коливання потоку через присутність виїмки, є конвективна нестійкість зсувного шару.

В другій фазі нестаціонарного режиму III, при Re_b=31250, як і в експериментальних дослідженнях, можна простежити два основні діапазони безрозмірних частот: 0.012¸0.018 та 0.05¸0.07. Відбувається нерегулярне чергування цих частот. Амплітуди коливань також не є сталими. Причина цього полягає в тому, що крім коливань, спричинених нестійкістю зсувного шару у верхній частині виїмки, нестаціонарну поведінку мають також інтенсивні вихорові утворення всередині. Комбінований вплив цих явищ і визначає кінцевий характер поведінки потоку в околі виїмки та нижче за течією.

Таблиця 1

	I	II		III
Reb	625	6700	15625	31250
d	0.04	0.012	0.008	0.0056
Red	395	1290	1975	2800
Red**	52	170	250	372
d/b	0.6	0.2	0.125	0.0896
b/d**	12	39	62.5	84.5
bRed1/2/d	31	186	356	593
St=fb/U¥	-	0.5	0.85	0.44¸0.59 1¸1.5
St=fd**/U¥	-	0.0128	0.014	0.005¸0.07 0.012¸0.018

ВИСНОВКИ

У дисертації наведено теоретичне дослідження проблем нестаціонарної взаємодії крупних вихорових збурень в потоку в’язкої рідини з пограничним шаром на поверхні твердих тіл, а також обтікання поверхні зі значною геометричною неоднорідністю (виїмкою) та відсмоктуванням частини рідини з пограничного шару через поверхню тіла. Одержані результати виявляють основні механізми та закономірності поведінки потоку в цих умовах, що дає змогу цілеспрямовано впливати на структуру потоку в різних режимах в залежності від параметрів потоку і геометрії поверхні, і таким чином керувати гідродинамічними характеристиками тіл.

Основні результати роботи полягають в наступному:

Розроблено фізико-математичну модель та реалізовано алгоритм чисельного аналізу стаціонарних та нестаціонарних течій в’язкої нестисливої рідини в присутності твердих границь, який базується на розв’язку нестаціонарних рівнянь Нав’є-Стокса в змінних завихреність - функція течії.

На основі чисельного розв’язку задачі в’язкого обтікання пластини з відсмоктуванням через відвідний канал, розташований під кутом до пластини, визначено умови існування безвідривного обтікання як над пластиною, так і в каналі. Одержано залежності від числа Рейнольдса, середнього розходу через канал, кута нахилу водоводу і комбінації цих параметрів.

Досліджено взаємодію детермінованих вихорів у в’язкому потоку з пластиною скінченної довжини. Вивчено процес руйнування вихорів при їх ударі з передньою кромкою пластини і подальший вплив на пограничний шар. Показано суттєву відмінність у структурі потоку, що виникає в результаті набігання на передню кромку пластини одиночного вихору та пари вихорів. Одержано залежності нестаціонарних характеристик обтікання пластини від циркуляції, розміру, початкового положення вихорів відносно передньої кромки пластини. Визначено умови виникнення відривного вихору біля передньої кромки пластини.

Досліджено обтікання поверхні, що має геометричну неоднорідність у вигляді однієї або декількох виїмок з гострими або гладенькими кромками. Показано існування стаціонарного та квазіперіодичного режиму потоку в околі виїмок в залежності від співвідношення параметрів основного потоку та геометричних розмірів виїмок. В стаціонарному режимі нульова лінія течія відділяє течію у виїмці від основного потоку, всередині виїмки існує циркуляційна течія з одним центром обертання. При квазіперіодичному режимі вздовж верхньої частини виїмки розвивається нестійкість зсувного шару, який сходить з передньої кромки і визначає частоту коливань як в районі виїмки, так і вниз за течією. У виїмці існує декілька вихорових зон з різним напрямком обертання рідини, які інтенсифікуються з підвищенням швидкості основного потоку. Наслідком їх впливу є поява двох діапазонів основних частот коливань.

Показано вплив дискретного вдуву/відсмоктування через стінки виїмок на структуру течії в околі виїмок в стаціонарному режимі в залежності від інтенсивності та місця його застосування на стінці.

 

ПУБЛІКАЦІЇ

1.         Воропаев Г.А., Розумнюк Н.В. Вязкое обтекание пластины с дискретным отсосом // Бионика. - 1992. - №25. - С.11-17

2.         Воропаєв Г.О., Розумнюк Н.В. Чисельне моделювання взаємодії одиночного вихору з пластиною // Вісник Київського Університету імені Тараса Шевченка. Математика. Механіка. - 1998. - Випуск 1. - С.53-58

3.         Розумнюк Н.В. Чисельний аналіз структури течії на поверхні з геометричною неоднорідністю // Вісник Донецького Університету. Серія А. - 2002. - №1. - С.176-179

4.         Voropaev G. A., Rozumniuk N. V. Effect of coherent structures on the boundary layer characteristics // Proc. Euromech Colloquium 327: Effects of organized vortex motion on heat and mass transfer. - 1994. - Kiev. - P.112-114

5.         Воропаев Г.А., Розумнюк Н.В. Вихревые структуры в сдвиговом потоке // Тез. докл.2 Cиб. cемин. Устойчивость гомог. и гетерог. жидкостей. - 1995. - Новосибирск. - С.14.

6.         Voropaev G. A., Rozumnyuk N. V. Interaction of a surface deformed continuously or discretely with a boundary layer // Proc.11^th European Drag Reduction Working Meeting. - 1999. - Prague. - P.79

7.         Voropaev G. A., Rozumnyuk N. V. A deformed and deformable surface as a means of boundary layer characteristics control // Proc. "ORGANIZED VORTICAL MOTION AS A BASIS FOR BOUNDARY-LAYER CONTROL". - Kiev. - 2000. - P.55

АНОТАЦІЯ

Розумнюк Н.В. В’язка взаємодія вихорових структур зі зсувною течією. - Рукопис.

Дисертація на здобуття наукового ступеня кандидата фізико-математичних наук за спеціальністю 01.02.05 - механіка рідини, газу та плазми. - Інститут гідромеханіки НАН України, Київ, 2003.

Дисертацію присвячено вивченню взаємодії пограничного шару на твердій поверхні з крупномасштабними вихоровими збуреннями у потоку в’язкої рідини на основі чисельного розв’язку нестаціонарних рівнянь Нав’є-Стокса в змінних завихреність - функція течії. Розглянуто процес спотворення форми вихору Ламба та його руйнування при взаємодії з гострою кромкою пластини, залежність інтенсивності взаємодії від початкових параметрів вихору та його положення відносно пластини. Показано вплив проходження вихору або пари вихорів на пограничний шар на різних боках пластини.

Досліджено параметри обтікання пластини при відсмоктуванні рідини через відвідний канал, розташований під різними кутами до поверхні. Показано існування безвідривного обтікання як у каналі, так і в зовнішньому потоку в залежності від кута нахилу каналу, інтенсивності відсмоктування та числа Рейнольдса.

Вивчено структуру потоку при обтіканні поверхні зі значною геометричною неоднорідністю у вигляді однієї або декількох виїмок різної форми та розміру. Проаналізовано характерні особливості течії всередині виїмок та її вплив на основний потік. Показано існування стаціонарного та квазіперіодичного режимів обтікання. Виявлено типові частотні характеристики коливань потоку в режимі зсувного шару.

Ключові слова: нестаціонарні течії, пограничний шар, детерміновані вихорові структури, геометрична неоднорідність.

АННОТАЦИЯ

Розумнюк Н.В. Вязкое взаимодействие вихревых структур со сдвиговым течением. - Рукопись.

Диссертация на соискание научной степени кандидата физико-математических наук по специальности 01.02.05 - механика жидкости, газа и плазмы. - Институт гидромеханики НАН Украины, Киев, 2003.

Диссертация посвящена изучению взаимодействия пограничного слоя на твердой поверхности с крупномасштабными вихревыми структурами в потоке вязкой жидкости на основании численного решения нестационарных уравнений Навье-Стокса в переменных завихренность - функция тока.

Исследованы параметры обтекания пластины при отсосе жидкости через отводной канал, расположенный под разными углами к поверхности пластины. Показано существование безотрывного обтекания в канале и во внешнем потоке в зависимости от угла наклона канала, интенсивности отсасывания и числа Рейнольдса.

Рассмотрен процесс искажения формы вихря Ламба и его разрушение при взаимодействии с острой кромкой пластины. Интенсивность взаимодействия зависит от начальных параметров вихря и его положения относительно пластины, а также от числа Рейнольдса. Скос потока в районе передней кромке, индуцированный приближеним конвективного вихря, изменяет его траекторию и вызывает отрыв на передней кромке пластины. Начальный вихрь разрезается пластиной на две части, которые перемещаются вдоль сторон пластины с разной скоростью. Их влияние на пограничный слой зависит от направления и величины продольной скорости в месте соприкосновения с пограничным слоем.

Два вихря с одинаковыми начальными размерами, но противоположной циркуляцией, и расположенные симметрично относительно пластины, не вызывают отрыв на носике. Вызванные ими изменения в пограничном слое определяются направлением вращения по отношению к местной завихренности. В случае несимметричного начального положения вихрей картина взаимодействия зависит от взаимного расположения вихрей и сдвига по вертикали относительно пластины.

Изучена структура потока при обтекании поверхности со значительной геометрической неоднородностью в виде одной или нескольких выемок различной формы и размера. Характерные особенности течения внутри выемок и их влияние на основной поток зависят как от геометрических размеров и формы выемок, так и от характеристик основного потока. Показано существование стационарного и квазипериодического режимов обтекания. В первом случае внутри выемки существует циркуляционное течение вокруг одного центра, отделенное от основного потока нулевой линией тока. При увеличении числа Рейнольдса в выемке формируется несколько зон с противоположным направлением завихренности. Течение носит квазипериодический во времени характер, обусловленный развитием неустойчивости сдвигового слоя, сходящего с передней кромки выемки. Взаимодействие этих возмущений с нижней кромкой и всем объемом выемки определяет типичные частотные характеристики колебаний потока в окрестности выемки и вниз по потоку. Полученные численно частоты колебаний в режиме сдвигового слоя соответствуют экспериментальным данным других авторов.

Ключевые слова: нестационарные течения, пограничный слой, детерминированные вихревые структуры, геометрическая неоднородность.

ABSTRACT

Rozumnyuk N. V. Viscous interaction of vortical structures with a shear flow. - Manuscript.

Thesis to acquire the academic degree of a candidate of physical and mathematical science in speciality 01.02.05 - mechanics of fluids, gas and plasma. - Institute of Hydromechanics of the National Academy of Sciences, Kyiv, 2003.

The dissertation investigates the interaction of a boundary layer over a rigid surface with large-scale vertical structures in a viscous flow, on the basis of numerical solutions of the nonstationary Navier-Stokes equations in the stream function - vorticity formulation. The process of distortion of the Lamb’s vortex during its interaction with a sharp edge of a plate has been investigated, as well as the strength of the interaction in dependence on initial parameters of the vortex and its location relative the plate. The effect of a single vortex passage, or two vortices, onto the boundary layer over different sides of the plate has been revealed.

Have been analyzed the parameters of the flow over a plate under suction through a canal inclined at varied angles. A possibility of an attached flow both in the canal and over the plate has been showed, in dependence on the slope of the canal, strength of suction and Reynolds number.

The structure of flow over a surface with large geometrical inhomogeneity in the form of a single groove of different shape and size, or a set of grooves, has been investigated. Typical features of flow inside grooves and the influence on the main flow have been analyzed. Possibility of stable or quasiperiodic regime of flow has been demonstrated. Typical frequencies of flow oscillations in the mode of shear flow have been revealed.

Key words: nonstationary flows, boundary layer, vortical structures, geometrical inhomogeneity.