Министерство образования РФ
Рязанская государственная радиотехническая академия
Кафедра ОиЭФ
Контрольная работа
«ИЗУЧЕНИЕ ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ С ПОМОЩЬЮ МАЯТНИКА МАКСВЕЛЛА»
Выполнил ст. гр. 731Пантюшин И.А.
Проверил Рязань 2007г.Цель работы: Изучение законов вращательного движения, экспериментальное определение моментов инерции сменных колец с помощью маятника Максвелла.
Приборы и принадлежности: установка с маятником Максвелла со встроенным миллисекундомером, набор сменных колец.
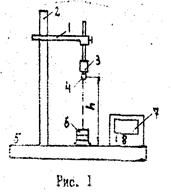
Элементы теорииПрибор с маятником Максвелла (и встроенным миллисекундомером) используется для изучения законов вращательного движения. По данным, которые снимаются с прибора, можно определить моменты инерции вращающихся (на установке) тел. На вертикальной стойке основания (с нанесённой на ней миллиметровой шкалой) крепятся два кронштейна. Верхний кронштейн электромагнитом и устройством регулировки бифилярного подвеса (на котором крепиться сам маятник). С помощью электромагнитов маятник со сменными кольцами фиксируется в верхнем исходом положении.
В нижний кронштейн вмонтирован фотоэлектрический датчик. Данный фотодатчик связан с миллисекундометром. Сам нижний кронштейн подвижен.
Введём условные обозначения: m1 - масса стержня с насаженным на него диском; d - диаметр стержня; D1, D2 - внутренний и внешний диаметры сменных колец соответственно; J1 - момент инерции стержня с диском относительно оси О; J -момент инерции сменного кольца относительно той же оси; mS - суммарная масса маятника со сменным кольцом; JS - суммарный момент инерции маятника со сменным кольцом относительно оси О.
Когда маятник находиться в верхнем положении, он обладает потенциальной энергией.
1)![]()
При движении маятника происходит преобразование энергии в кинетическую. Кинетическую энергию маятника, когда он находиться в нижнем положении можно записать так.
2)![]()
Где V2 - поступательная скорость движения центра маятника; w - угловая скорость вращения маятника.
Учитывая закон сохранения энергии
3)![]()
При ![]() , получим:
, получим:
4)![]()
Если маятник опустился на расстояние h за время t, то исходя из кинематических соотношений для равноускоренного движения можно записать следующую формулу.
5)![]()
Выразим JS из (4) и (5).
6)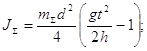
Учтя JS= J1 + J2 , формулу (6) можно записать так.
7)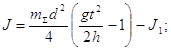
Таким образом, измеряя t, h и J1, можно найти момент инерции Jсменного кольца.
Расчётная часть| m2, кг | № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|
| 0,20 | t1, с | 2,18 | 2,11 | 2,12 | 2,11 | 2,16 | 2,09 | 2,05 | 2,06 | 2,33 | 2,38 | 2,16 |
| 0,31 | t2, с | 2,27 | 2,48 | 2,28 | 2,50 | 2,29 | 2,37 | 2,39 | 2,32 | 2,33 | 2,53 | 2,38 |
| 0,41 | t3, с | 2,48 | 2,45 | 2,35 | 2,33 | 2,31 | 2,52 | 2,37 | 2,52 | 2,34 | 2,51 | 2,42 |
Для удобства введём обозначение i – ой величины, для вычисления некоторых величин для i – ого кольца.
Сняв измерения с установки, имеем значения следующих величин:
D1 = 9´10-2 м.; D2 = 13´10-2 м.; (длина хода маятника) h = 0,34 м. при данной погрешности Dh = 2´10-3 м.;
m1 = 0,134 кг.; DmS = 10-3 кг.; d = 10-2 м.; J1 = (1,1 ± 0,1)´10-4 кг´м2.; Dtсист = 5´10-3 с.;
действительные значения времени ![]() соответственно серии замеров для каждого из колец (занесены в таблицу).
соответственно серии замеров для каждого из колец (занесены в таблицу).
Найдём погрешность измерения времени (Dt).
![]() При
При 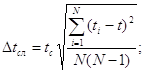 где tс = 2,26
где tс = 2,26
![]() = 0,08 с.
= 0,08 с.
![]() = 0,07 с.
= 0,07 с.
![]() = 0,06 с.
= 0,06 с.
Представим Dtсл, как действительное значение ![]() и найдём его по данной формуле от Dt1сл, Dt2сл и Dt3сл.
и найдём его по данной формуле от Dt1сл, Dt2сл и Dt3сл.
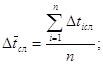
![]() с.;
с.; ![]()
![]() с.;
с.;
Далее вычислим моменты инерции J каждого из сменных колец по формуле (7).
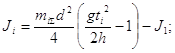
![]()
![]() кг´м2.
кг´м2.
![]() кг´м2.
кг´м2.
![]() кг´м2.
кг´м2.
Оценим погрешность найденных значений Ji, используя следующую формулу.
![]() при DJ1 = 10-5 кг´м2.
при DJ1 = 10-5 кг´м2.
Учтём, что 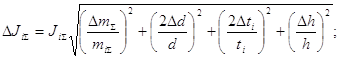
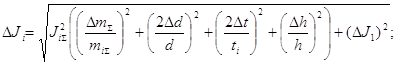
Где JS вычисляется по формуле (6). Учтём, что
![]()
при c – цена деления прибора которым измерялась величина d.
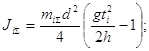
DJ1 = DJ0 (для погрешности момента инерции маятника без кольца)
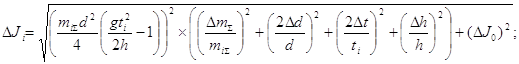
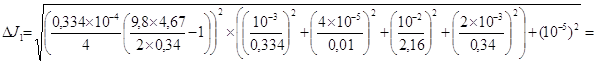 = 1,12´10-5 кг´м2.
= 1,12´10-5 кг´м2.
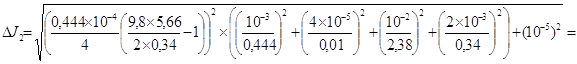 = 1,26´10-5 кг´м2.
= 1,26´10-5 кг´м2.
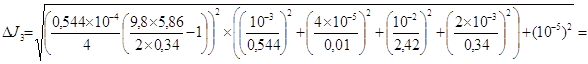 = 1,38´10-5 кг´м2.
= 1,38´10-5 кг´м2.
Теперь рассчитаем моменты инерции сменных колец по следующей формуле.
![]()
![]() кг´м2.
кг´м2.
![]() кг´м2.
кг´м2.
![]() кг´м2.
кг´м2.
Вычислим для каждого кольца погрешность моментов инерции (Jiтеор), найденные по предидущей формуле.
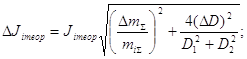 При
При ![]() .
.
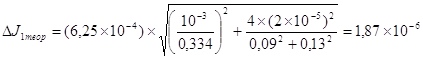 кг´м2.
кг´м2.
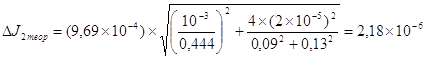 кг´м2.
кг´м2.
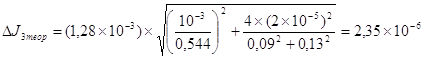 кг´м2.
кг´м2.
| m2, кг | Jэксп,кг´м2 | Jтеор,кг´м2 |
| 0,2 | 4,44´10-4 ± 1,12´10-5 | 6,25´10-4 ± 1,87´10-6 |
| 0,31 | 7,84´10-4 ± 1,26´10-5 | 9,69´10-4 ± 2,18´10-6 |
| 0,41 | 1,02´10-3 ± 1,38´10-5 | 1,28´10-3 ± 2,35´10-6 |
Похожие работы
... самопроизвольно протекать не может, необходим подвод энергии извне. 2-й закон термодинамики с использованием понятия энтропии формулируется так: Все процессы в природе протекают в направлении увеличения энтропии, энтропия замкнутой системы не может самопроизвольно уменьшаться. В статистической физике энтропию связывают с термодинамической вероятностью состояния системы – с числом ...
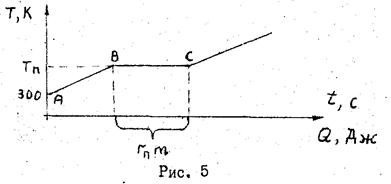
... изменение. 3. Что такое термодинамическая вероятность состояния (статистический вес). 4. Статистический смысл изменения энтропии. 5. Первый закон термодинамики. 6. Вывод рабочей формулы (36) данной работы. 7. Второй закон термодинамики и его статистический смысл. 6. ОПРЕДЕЛЕНИЕ ТЕМПЕРАТУРЫ И УДЕЛЬНОЙ ТЕПЛОТЫ ПЛАВЛЕНИЯ МЕТАЛЛА Цель работы Исследовать фазовый переход первого рода ...
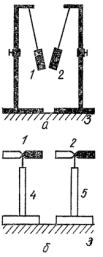
... рассматриваться как определенные независимо одна от другой. Зависимость между силой, массой и ускорением. Второй закон Ньютона Данную зависимость с точностью, которая возможна в демонстрационном эксперименте, устанавливают на опыте, Поскольку согласно принятой в стабильном учебнике методике сначала устанавливается только способ задания некоторой силы «безразлично какой именно!», в опытах ...
... школа, 1988. 10. Артюхов В.Г., Ковалева Т.А., Шмелев В.П. Биофизика. Воронеж: Воронежский гос. ун-т 1994. 11. Антонов В.Ф. Биофизика. VI.: Арктос-Викапресс, 2000. 12. Дополнительная 13. Механика и биомеханика 14. Никитин E. VI. Теоретическая механика. VI.: Наука. 1968. Александер Р. Биомеханика. VI.: Мир. 1970. 15. Журавлева А.И., Iраевская И.Д. Спортивная медицина и лечебная ...





0 комментариев