Министерство образования РФ
Рязанская государственная радиотехническая академия
Кафедра ОиЭФ
Контрольная работа
«ИЗУЧЕНИЕ УПРУГОГО И НЕУПРУГОГО УДАРОВ ШАРОВ»
Выполнил ст. гр. 255Ампилогов Н. В.
ПроверилМалютин А. Е
Рязань 2002г.Цель работы: изучение законов сохранения импульса и механической энергии на примере ударного взаимодействия двух шаров; определение средней силы удара, коэффициента восстановления скорости и энергии деформации шаров.
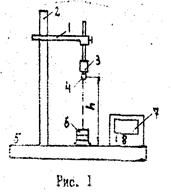
Приборы и принадлежности: установка для изучения упругого и неупругого ударов шаров ФПМ-08.
Элементы теорииУдар (соударение) – это столкновение двух или нескольких тел, при котором взаимодействие длиться очень короткое время. При этом часть энергии данных тел полностью или частично переходит в потенциальную энергию упругой деформации или во внутреннюю энергию тел.
В качестве меры механического взаимодействия тел при ударе вместо ударной силы ![]() служит её импульс за время удара.
служит её импульс за время удара.
1) 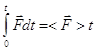
где <![]() > - средняя сила удара; t – время ударного взаимодействия.
> - средняя сила удара; t – время ударного взаимодействия.
Если импульс изменяется на конечную величину D(m![]() ) за время t, то из второго закона динамики следует, что
) за время t, то из второго закона динамики следует, что
2) ![]()
Тогда <F> можно выразить так
3) ![]()
где m1 и m2 – массы взаимодействующих тел; DV1 и DV2 изменение скоростей данных тел при ударе.
Абсолютно упругий удар – это удар при котором механическая энергия тел не переходит в другие механические виды энергии, и кинетическая энергия переходит полностью в потенциальную энергию упругой деформации (затем обратно).
Абсолютно неупругий удар – это удар при котором потенциальной энергии не возникает, кинетическая энергия полностью или частично переходит во внутреннюю энергию. Суммарный импульс данной системы сохраняется, а большая часть кинетической энергии переходит в тепло.
Линяя удара – это линия перпендикулярная поверхностям соударения обоих тел и проходящая через точку касания данных тел при ударе.
Прямой удар – есть удар, при котором вектора скоростей движения центров масс данных тел параллельны линии удара (перед непосредственным взаимодействием).
Центральный удар – это прямой удар, при котором центры масс соударяющихся тел лежат на линии удара.
Косой удар – это удар не являющийся прямым.
В данном случае будем считать, что система шаров на экспериментальной установке является изолированной. Тогда на основании законов сохранения импульса и энергии будет справедлива следующая формула
4) ![]()
5) ![]() ,
,
6) где m1 и m2 – массы шаров; ![]() ,
, ![]() и
и ![]() ,
, ![]() - их скорости до и после взаимодействия.
- их скорости до и после взаимодействия.
Из (4) и (5) выражаем скорости шаров после столкновения ![]() и
и ![]()
7) ![]() 7)
7) ![]()
В данном случае рассматривался – абсолютно упругий удар. Но в действительности кинетическая энергия тел после соударения становиться меньше их первоначальной энергии на величину, которую можно найти так:
8) ![]() ,
,
где Kс – коэффициент восстановления скорости. Эта часть кинетической энергии тел при ударе преобразуется в их внутреннюю энергию.
Коэффициент восстановления скорости можно найти по следующей формуле:
9) 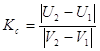
Если при соударении потеря кинетической энергии отсутствует (Kс = 1), то удар называется абсолютно упругим, а при Kс = 0 абсолютно неупругим. Если же 0 < Kс < 1, то удар является не вполне упругим.
Применительно к соударяющимся шарам, один из которых покоится, формулу (4) можно записать так:
10) ![]() , а для абсолютно неупругого удара
, а для абсолютно неупругого удара ![]() .
.
Скорости шаров до и после удара можно определить по формулам:
11) ![]() ; 12)
; 12) ![]() ; 13)
; 13) ![]()
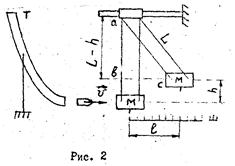
где l – расстояние от точки подвеса до центра тяжести шаров (l = 470 ± 10 мм.), a0 – угол бросания правого шара, a1 и a2 – углы отскока соответствующих шаров.
Расчётная часть
| № | ti´10-6 | Dti´10-6 | (Dti´10-6)2 | a1i | Da1i |
| a2i | Da2i |
|
| 1 | 76 | -14 | 196 | 2° | -0,5° | 0,25° | 12° | -0,2° | 0,04° |
| 2 | 103 | 13 | 169 | 2° | -0,5° | 0,25° | 13° | 0,8° | 0,64° |
| 3 | 96 | 6 | 36 | 3° | 0,5° | 0,25° | 11° | -1,2° | 1,44° |
| 4 | 93 | 3 | 9 | 2,5° | 0° | 0° | 13° | 0,8° | 0,64° |
| 5 | 82 | -8 | 64 | 3° | 0,5° | 0,25° | 12° | -0,2° | 0,04° |
|
|
|
| |||||||
После работы с установкой имеем значение следующих величин: (угол бросания правого шара) a0 = 15°![]() ; (массы правого и левого шаров соответственно) m1 = 112,2 ´ 10-3 кг, m2 = 112,1 ´ 10-3 кг; (длина бифилярных подвесов обоих шаров) l = 470 ´ 10-3 м; (погрешность значения длин бифилярных подвесов) Dl = 0,01 м; (цена деления микросекундометра) ct = 10-6; (цена деления градусных шкал) ca = 0,25°.
; (массы правого и левого шаров соответственно) m1 = 112,2 ´ 10-3 кг, m2 = 112,1 ´ 10-3 кг; (длина бифилярных подвесов обоих шаров) l = 470 ´ 10-3 м; (погрешность значения длин бифилярных подвесов) Dl = 0,01 м; (цена деления микросекундометра) ct = 10-6; (цена деления градусных шкал) ca = 0,25°.
При известном среднем арифметическом значении времени ![]() найдём погрешность измерения данной величины:
найдём погрешность измерения данной величины:
![]()
![]()
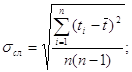
![]()
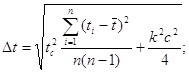
![]() с.
с.
![]()
![]()
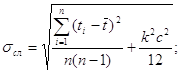
![]() с.
с.
При известных значениях ![]() и
и ![]() найдём погрешность их измерения (в радианах, при p = 3,14):
найдём погрешность их измерения (в радианах, при p = 3,14):
![]() рад.
рад.
![]() рад.
рад.
![]() рад.
рад.
![]() рад.
рад.
![]() при Dсл » 0;
при Dсл » 0;![]()
![]() рад.
рад.
![]() при sсл » 0; sa0 = sс;
при sсл » 0; sa0 = sс; ![]() ;
;
![]() рад.
рад.
Теперь найдём скорости данных шаров до соударения (V1, V2) и их скорости после взаимодействия (U1, U2). При этом (скорость левого шара) V2 = 0 т. к. он покоиться до удара. Значения остальных скоростей находят из следующих формул (через l, a и g):
![]()
![]()
![]()
![]() м/с2;
м/с2; ![]() м/с2;
м/с2; ![]() м/с2;
м/с2;
Найдём погрешности вычисления данных скоростей.
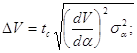
![]() м/с.
м/с.
![]() м/с.
м/с.
![]() м/с.
м/с.
По формуле (3) найдём (силу кратковременного взаимодействия шаров) < F >. Учитывая, что DV1 = |U1 - V1| и DV2 = |U2 – V2|.
![]()
![]() Н.
Н.
![]()
![]() Н.
Н.
Значение силы удара шаров найдём, как действительное значение от < F1 > и < F2 >:![]()
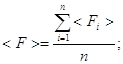
![]() Н.
Н.
Найдём погрешность величины < F > по формуле
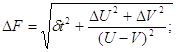 (погрешность вычисления массы пренебрежимо мала)
(погрешность вычисления массы пренебрежимо мала)
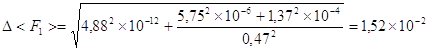 Н.
Н.
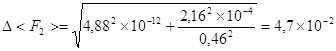 Н.
Н.
![]() Н.
Н.
Далее по формуле (9) найдём коэффициент восстановления скорости Kс:
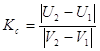 ; при V2 = 0,
; при V2 = 0, 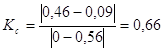
Пользуясь формулой для вычисления погрешности косвенных величин 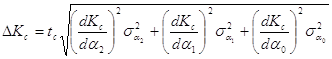
Найдём DKс. Для получения более точного значения погрешности, используя формулы (11, 12, 13), сведём исходную формулу для вычисления Kс (9) к формуле с аргументом состоящим только из значений прямых измерений (t,a1,a2).
![]()
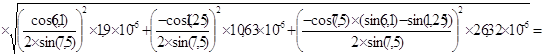
= 4,6 ´ 10-2
Теперь по формуле (8) вычислим значение энергии деформации шаров DEk:
![]()
![]() Дж.
Дж.
Осталось найти погрешность D(DEK). При использовании следующей формулы предполагается, что V1 и Kс являются прямыми измерениями.
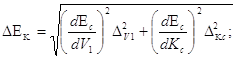 DEK = 0,17 Дж.
DEK = 0,17 Дж.
Похожие работы
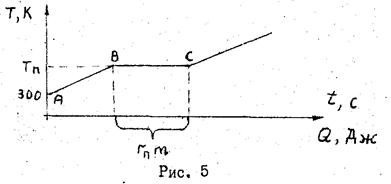
... изменение. 3. Что такое термодинамическая вероятность состояния (статистический вес). 4. Статистический смысл изменения энтропии. 5. Первый закон термодинамики. 6. Вывод рабочей формулы (36) данной работы. 7. Второй закон термодинамики и его статистический смысл. 6. ОПРЕДЕЛЕНИЕ ТЕМПЕРАТУРЫ И УДЕЛЬНОЙ ТЕПЛОТЫ ПЛАВЛЕНИЯ МЕТАЛЛА Цель работы Исследовать фазовый переход первого рода ...
... , нужно посредством правил подсчета значащих цифр округлить результат математических вычислений так, чтобы точность их соответствовала точности данных, полученных от измерения. ИЗУЧЕНИЕ КИНЕМАТИКИ И ДИНАМИКИ ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ НА МАШИНЕ АТВУДА Цель работы Экспериментальная проверка основных уравнений и законов поступательного движения тела на специально сконструированной для этого ...
... в 2 раза. 180. Найти относительную скорость движения двух частиц, движущихся навстречу друг другу со скоростями u1 = 0,6×c и u2 = 0,9×c. II. ОСНОВЫ МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ Молекулярная физика и термодинамика – разделы физики, в которых изучаются макроскопические процессы в телах, связанные с огромным числом содержащихся в них атомов и молекул (макроскопические системы ...
... 17.6 - 2.5 2 22.5 109.4 20.1 16.7 - 3.4 - 2.8 3 22.5 175. - 2.4 Задание 4. Проверка закона сохранения импульса. ОТЧЕТ ……………………………………………………………………………. о выполнении лабораторной работы №2 Законы сохранения в механике. Колебательное движение Задание 1. Исследование затухания колебаний маятника Упражнение 1. Закон затухания. Таблица 1. ...







0 комментариев