Визначення площі між функціями інтегралом за методом трапеції на мові Pascal

Зміст

1. Постановка задачі 3

2. Математичний опис рішення задачі 4

3. Алгоритм програми. 6

4. Лістинг програми. 7

5. Контрольний приклад. 10

Список використаної літератури. 11

Постановка задачі

 

Скласти програму на мові Pascal розрахунку за методом трапецій площі між графіками функцій F1(x) = cos x² + 1 i F2(x) = 2^{x^2} з точністю е = 0,0001.

 

2. Математичний опис рішення задачі

Розрахунок за методом трапецій площі між графіками функцій F1(x) = cos x² + 1 i F2(x) = 2^{x^2} (рис.1) здійснюється вирішенням визначеного інтегралу 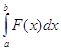, який саме і визначає площі під графіками. За властивістю інтегралів  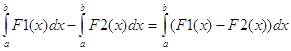, тому в якості підінтегральної функції ми беремо функцію F(x) = cos x² + 1 - 2^{x^2}

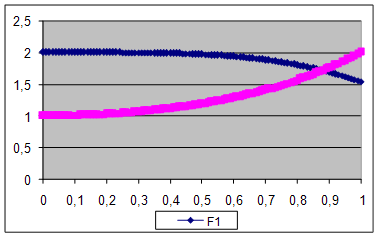
Рис.1.

Саме метод трапеції реалізований на мові Pascal у наступному фрагменту програми, у якому для розрахунків використано цикл із заздалегідь визначеним числом повторень:

h:=(b-a)/n;

yp:=0;

x:=a;

for i:=1 to n-1 do

begin

 x:=x+h;

yp:=yp+(cos(sqr(x))+1-exp(sqr(x)*ln(2)));

end;

yn:=cos(sqr(a))+1-exp(sqr(a)*ln(2));

yk:=cos(sqr(b))+1-exp(sqr(b)*ln(2));

s:=((yk+yn)/2+yp)*h;

де,

n – кількість відрізків, на які розбивається дільниця інтегрування;

i – допоміжна змінна циклу;

a – початкова межа інтегрування;

b – кінцева межа інтегрування;

h – довжина відрізку інтегрування;

yn – значення підінтегральної функції в початкової точці (точка а);

yk – значення підінтегральної функції в кінцевої точці (точка а);

yp – одне з проміжних значень підінтегральної функції;

s – потрібне значення визначеного інтегралу (площа) за методом трапецій.

 

3. Алгоритм програми

Алгоритм програми наведено на рис.2.

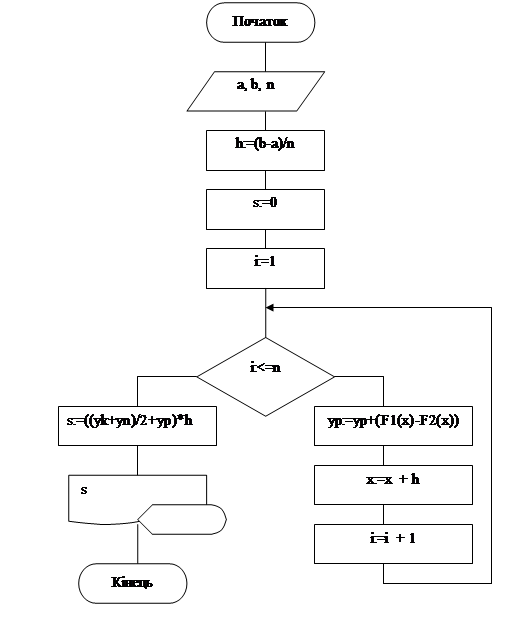
Рис.2. Алгоритм програми

4. Лістинг програми

Лістинг програми наведений нижче:

unit Unit1;

interface

uses

Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,

Dialogs, ExtCtrls, StdCtrls;

type

TForm1 = class(TForm)

StaticText1: TStaticText;

StaticText2: TStaticText;

StaticText3: TStaticText;

StaticText4: TStaticText;

Edit1: TEdit;

Edit2: TEdit;

Edit3: TEdit;

Edit4: TEdit;

Button1: TButton;

Button2: TButton;

Image1: TImage;

Button3: TButton;

procedure Button1Click(Sender: TObject);

procedure Button2Click(Sender: TObject);

procedure Button3Click(Sender: TObject);

private

{ Private declarations }

public

{ Public declarations }

end;

var

Form1: TForm1;

implementation

{$R *.dfm}

procedure TForm1.Button1Click(Sender: TObject);

var a,b,s,h,x,yp,yn,yk:real; i,n:integer;

begin

a:=StrtoFloat(Edit1.Text);

b:=StrtoFloat(Edit2.Text);

n:=StrtoInt(Edit3.Text);

h:=(b-a)/n;

yp:=0;

x:=a;

for i:=1 to n-1 do

begin

x:=x+h;

yp:=yp+(cos(sqr(x))+1-exp(sqr(x)*ln(2)));

end;

yn:=cos(sqr(a))+1-exp(sqr(a)*ln(2));

yk:=cos(sqr(b))+1-exp(sqr(b)*ln(2));

s:=((yk+yn)/2+yp)*h;

Edit4.Text:=copy(FloattoStr(s),1,6)

end;

procedure TForm1.Button2Click(Sender: TObject);

begin

Edit1.Text:='';

Edit2.Text:='';

Edit3.Text:='';

Edit4.Text:='';

end;

procedure TForm1.Button3Click(Sender: TObject);

begin

close

end;

end.

5. Контрольний приклад

У перше поле вводимо початкове значення відрізку інтегрування, наприклад, 0;

у друге поле вводимо кінцеве значення відрізку інтегрування, наприклад, 0,5 (причому десяткову частину дробу відділяємо комою); кількість меж, на які буде розбито відрізок інтегрування вводимо у трете поле, наприклад, 10000 (чім більше, тім точніше результат); натискаємо кнопку Розрахувати. Розрахована площа фігури між лініями графіків, та межами 0 і 0,5 з’являється у четвертому останньому полі і дорівнюватиме 0,4664 (рис.3).

 

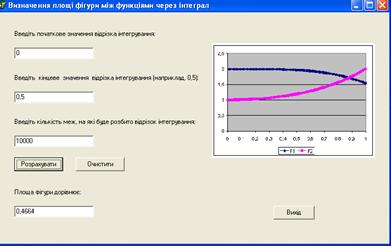
Рис.3.

Список використаної літератури

1.       Фаронов В.В. Pascal. Начальный курс. Учебное пособие, - М.: Номидж, 1997, - 616 с.

2.       Руденко В.Д., Макарчук О.М., Патланжоглу М.О. Практичний курс інформатики /За ред. В.М.Мадзігона. - К: Фенікс, 1997.

3.       Інформатика та комп'ютерна техніка: Навч.-метод. посібник / За заг. ред. О.Д.Шарапова. – К.: КНЕУ, 2002. – 534 с.

4.       Я.М. Глинський. Інформатика: Навч. посібник для загальноосвітніх навчальних закладів. – Львів: «Деол», 2002. – 256 с.