БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Кафедра РТС
РЕФЕРАТ
На тему:
«Колебательные, инерционно-дифференцирующие и интегрирующие звенья радиотехнических следящих систем»
МИНСК, 2008
К колебательным звеньям относят звенья, описываемые дифференциальным уравнением следующего вида:
![]()
где ξ – коэффициент затухания (для звеньев автоматических систем ξ = 0,5…0.7).
К таким звеньям относятся RLC контура, акселерометры и др.
Обозначим ![]() (собственная частота) и разделим почленно все слагаемы числителя и знаменателя на Т2; в результате получим:
(собственная частота) и разделим почленно все слагаемы числителя и знаменателя на Т2; в результате получим:
![]()
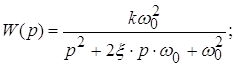
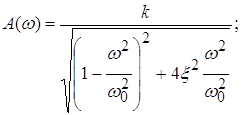
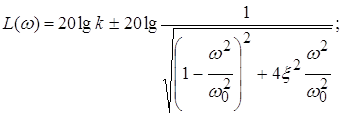
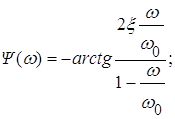
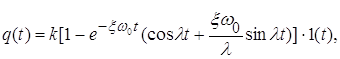
где ![]() – частота затухающих колебаний;
– частота затухающих колебаний;
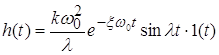 .
.
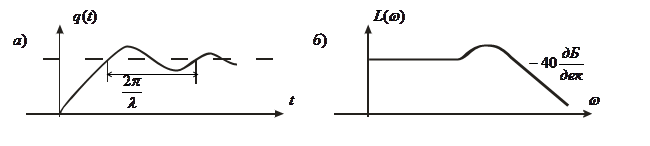
Рис. 1. Переходная и логарифмическая амплитудно-частотная характеристики колебательного звена.
По мере увеличения ξ, длительность переходного процесса увеличивается, частота колебаний уменьшается и при ![]() процесс может быть описан ДУследующего вида:
процесс может быть описан ДУследующего вида:
![]() или
или
![]() ,
,
где![]() ,
, 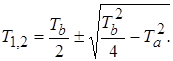
Такое звено называется апериодическим звеном 2-го порядка. Передаточная функция звена определяется выражением
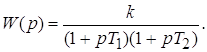
Апериодическое звено 2ого порядка может быть представлено как два последовательно соединенных апериодических звена 1ого порядка. Характеристики звена:
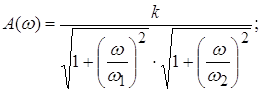
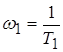 и
и 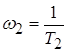 – сопрягающие частоты.
– сопрягающие частоты.
ЛАЧХ (рис.3.9): 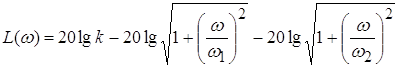
ФЧХ: ![]()
Переходная характеристика (рис.2):
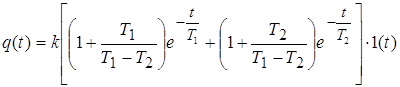 .
.

Рис. 2. Переходная и логарифмическая амплитудно-частотная характеристики апериодического звена 2-го порядка
Дифференцирующие звенья. К идеальным дифференцирующим звеньям
относят звенья, выходная величина которых пропорциональна производной входной величины:
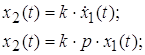
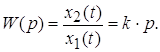
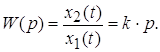
В автоматических системах единственным примером идеального дифференцирующего звена является тахогенератор.
Величина k имеет размерность времени, называется постоянной времени дифференцирования и обозначается Т.
Она может быть определена, если входные и выходные величины имеют одну и ту же физическую природу следующим образом: постоянная времени определяется как интервал времени от момента подачи на вход линейно изменяющегося напряжения до момента времени, когда напряжение на выходе сравняется с напряжением на входе (рис. 3).
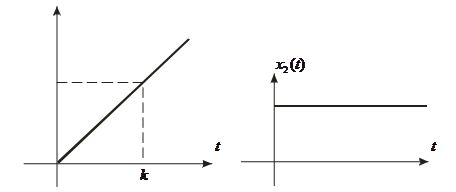
Рис.3. К определению постоянной времени идеального дифференцирующего звена
Характеристики идеального дифференцирующего звена:
![]() ;
; ![]() ;
; ![]() ; q(t) = k δ(t);
; q(t) = k δ(t);
![]() .
.
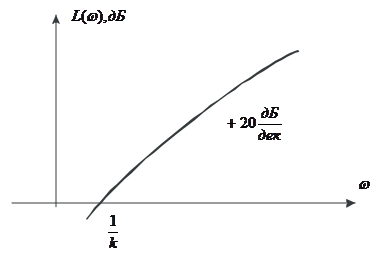
Рис. 4. ЛАЧХ идеального дифференцирующего звена
К инерционным дифференцирующим звеньям относятся звенья, имеющие следующие характеристики:
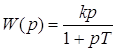 ;
; 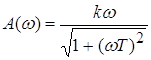 ;
; ![]() ;
; ![]() .
.
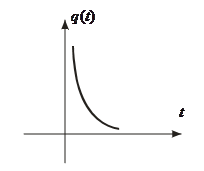
Рис.5. Переходная характеристика инерционного дифференцирующего звена
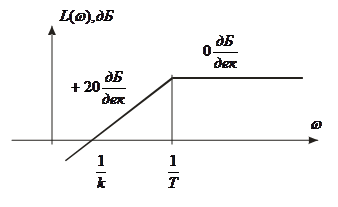
Рис. 6. ЛАЧХ инерционного дифференцирующего звена
Примером инерционного дифференцирующего звена является RC цепь (рис. 6).
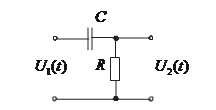
Рис. 7. Схема инерционного дифференцирующего звена
Форсирующее звено представляет собой параллельное соединение безынерционного и идеального дифференцирующего звеньев:
![]() .
.
Звено используется для коррекции передаточных функций систем (компенсирует запаздывание фазы, вносимое интегрирующими звеньями).
Характеристики звена (рис.7):
![]() ;
;
![]() ;
; ![]() .
.
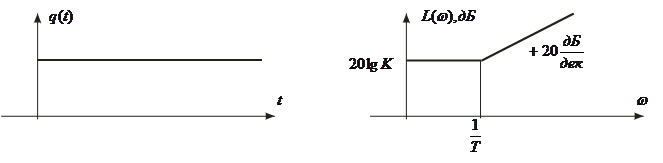
Рис. 8. Характеристики форсирующего звена
Интегрирующие звенья. К идеальным интегрирующим звеньям относят звенья, выходная величина у которых равна интегралу от входной величины:
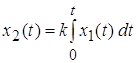 ;
;
![]()
где ![]() ; Т – постоянная времени звена.
; Т – постоянная времени звена.
Если физическая природа входной и выходной величин одинакова (например, напряжение) постоянная времени определяется как интервал времени от момента подачи на вход постоянного напряжения до момента времени, когда напряжение на выходе сравняется с напряжением на входе ( рис.8).
![]()
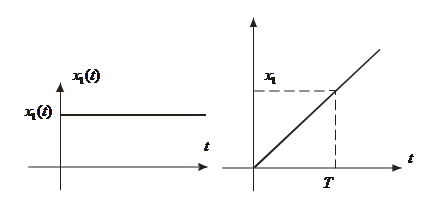
Рис.9. К определению постоянной времени идеального интегрирующего звена
Характеристики идеального интегрирующего звена (рис. 9) определяются следующими выражениями:
![]() ;
; 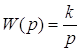 ;
; 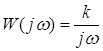 ;
; ![]() ;
;
![]() ;
; ![]() .
.
Примером такого звена является исполнительный двигатель, у которого угол поворота ротора равен интегралу от входного напряжения.
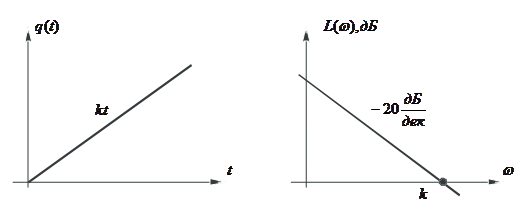
Рис.10. Характеристики идеального интегрирующего звена
К инерционным интегрирующим звеньям относятся звенья, передаточная функция которых определяется выражением:
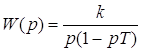 ;
;
Другие характеристики звена (рис.11):
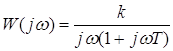 ;
; 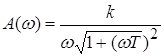 ;
;
![]() ;
; ![]()
Это звено можно рассматривать как последовательное соединение апериодического звена 1-го порядка и идеального интегратора.
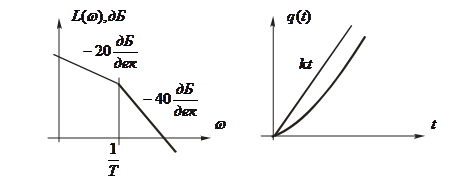
Рис.11. Характеристики инерционного интегрирующего звена
Изодромное звено представляет параллельное соединение безынерционного и идеального интегрирующего звеньев:
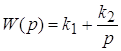 =
= 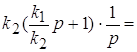
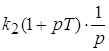
где ![]() .
.
Характеристики звена:
![]() ;
; ![]() ;
; ![]()
Переходная характеристика и ЛАЧХ звена изображены на рис.12.
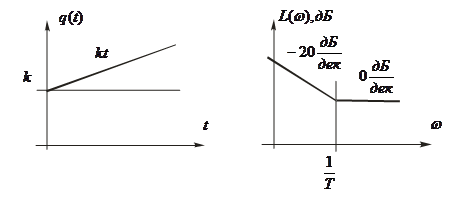
Рис.12. Характеристики изодромного звена
Звено временного запаздывания не входитв приведенную выше классификацию, однако вследствие широкого применения в схемах следящих систем целесообразно привести его характеристики:
![]()
![]() ;
; ![]() .
.
Звено может быть представлено как n последовательно соединенных апериодических звеньев 1 – го порядка.
ЛИТЕРАТУРА
1. Коновалов. Г.Ф. Радиоавтоматика: Учебник для вузов. – М.: Высш.шк., 2000.
2. Радиоавтоматика: Учеб. пособие для вузов./ Под ред. В.А. Бесекерского.- М.: Высш. шк., 2005.
3.. Первачев. С.В Радиоавтоматика: Учебник для вузов.- М.: Радио и связь, 2002.
4. Цифровые системы фазовой синхронизации/ Под ред. М.И. Жодзишского – М.: Радио, 2000
Похожие работы
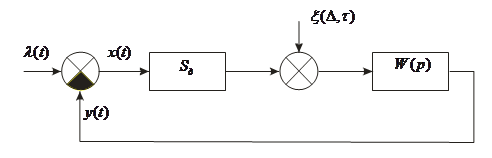
... в точке подачи обратной связи и определяется как передаточная функция от ошибки x(t) к управляемой величине y(t) . Передаточные функции в обобщенной структурной схеме радиотехнической следящей системы Основная передаточная функция – передаточная функция замкнутой системы. Определяется отношением изображений по Лапласу управляемой величины и задающего воздействия: где Передаточная ...
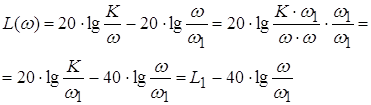
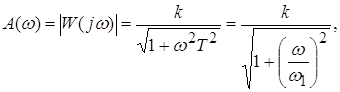
0 комментариев