Задача № 1.3-1. Водяной пар при давлении Р1 = 20 бар с температурой t1 = 400 °C при истечении из сопла расширяется по адиабате до давления Р2 = 2 бар. Определить площадь минимального выходного сечения сопла, а также скорость потока пара в этих сечениях, если расход пара равен М = 4 кг/с. Изобразить процесс в h – S координатах.
Пример. Определить скорость истечения пара из котла в атмосферу, если его давление P1 = 12 бар и температура t1 = 300 °C. Барометрическое давление равно РБ = 750 ммHg.
Задачу решить для двух условий: а) истечение происходит через цилиндрическое сопло, б) через расширяющиеся сопло. Изобразить процесс истечения в h – S координатах.
Решение. Отношение давлений Р2/Р1 = 1/12 = 0,0834 < (0,546 = βкр). В первом случае давление в выходном сечении не может быть меньше РКР, которое определяется как Р2КР = Р1βкр = 12 бар × 0,546 = 6,6 бар.
Тогда скорость истечения будет критической и равна (значение энтальпии находится по диаграмме h – S (см. рис.8.6).
Во втором случае давление в выходном сечении может быть меньше критического, а именно равно атмосферному Р2 = 1 бар, и тогда скорость истечения будет больше критической.
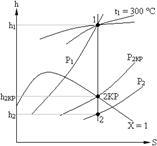
Рис. 1.6.
Задача № 1.3-2. Пар давлением Р1 = 18 бар и Х1 = 0,92 вытекает в среду с давлением Р2 = 12 бар, площадь выходного сечения сопла f = 20 мм2. Определить скорость истечения пара, его секундный расход, и изобразить процесс в h – S координатах.
Задача № 1.3-3. Пар давлением Р1 = 16 бар и Х1 = 0,95 вытекает из сопла Лаваля в среду с давлением Р2 = 2 бар. Расход пара m = 6 кг/с. Определить скорость истечения пара, а также сечение сопла Лаваля: а) считая пар идеальным газом и приняв К = 1,3 и б) реальным газом.
Задача № 1.3-4. Пар при Р1 = 20 бар и t1 = 350 °C расширяется в сопле до Р2 = 1 бар. Пренебрегая потерями трения и считая расширение адиабатным, определить объемный и массовый расход пара, и его критическую скорость, если выходное сечение сопла f2 = 500 мм2. Изобразить процесс в h – S координатах.
Задача № 1.3-5. Пар при Р1 = 120 бар и t1 = 500 °C расширяется в сопле до Р2 = 50 бар. Определить вид сопла, критическую и выходную скорость пара, критическое и выходное сечение сопла, если скоростной коэффициент φ = 0,96, а расход пара m = 2,78 кг/с. Изобразить процесс в h – S координатах.
Задача № 1.3-6. Сухой насыщенный пар при Р1 = 10 бар расширяется в сопле до Р2 = 6 бар. Определить расход пара через сопло, если скоростной коэффициент φ = 0,97; а f2 = 365 мм2. Изобразить процесс в h – S координатах.
Задача № 1.3-7. В калориметре пар дросселируется до давления Р2 = 1 бар, t2 = 130 °C. Определить начальное состояние пара и изменение его параметров (P, v, t, S, h, u), если Р1 = 20 бар. Изобразить процесс в h – S координатах.
Задача № 1.3-8. Пар при Р1 = 12 бар и t1 = 350 °C дросселируется до Р2 = 5 бар и подается на турбину паросиловой установки с температурой конденсата 32,88 °C. На сколько работоспособность пара уменьшится после дросселирования по сравнению с начальным состоянием?
Пример. Пар с давлением Р1 = 18 бар и температурой t1 = 250 °C дросселируется до Р2 = 10 бар. Определить параметры и функции состояния пара и степень перегрева в конце процесса дросселирования.
Решение. По диаграмме h – S (см. рис.8.7) находим начальное состояние пара, точка 1. Принимая h1 = h2, находим конечное состояние пара, точка 2.
Степень перегрева пара определяется как:
Δtn1 = tn1 – tH1 = 250 °C – 208 °C = 42 °C,
Δtn2 = tn2 – tH2 = 234 °C – 180 °C = 54 °C.
Параметры и функции состояния пара: v1 = 0,125 м3/кг; S1 = 6,61 кДж/(кг×К); u1 = 2889 кДж/кг; h1 = h2 = 2911 кДж/кг; v2 = 0,225 м3/кг; S2 = 6,86 кДж/(кг×К); u2 = 2887 кДж/кг.
Задача № 1.3-9. До какого давления необходимо дросселировать пар, имеющий давление Р1 = 60 бар и степень сухости Х = 0,96, чтобы он стал сухим насыщенным?
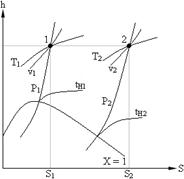
Рис. 1.7.
Прямые термодинамические циклы – циклы паротурбинных установок. Краткая теоретическая частьЦикл, в результате которого получается положительная работа называется прямым циклом, или циклом теплового двигателя.
Термический КПД цикла Карно имеет наибольшее значение по сравнению с КПД любого цикла, осуществляемого в одном и том же интервале температур. Поэтому их сравнение позволяет делать заключение о степени совершенства использования теплоты в машине.
Однако не всегда удается осуществить цикл Карно и процессы его сопровождающие. Так, цикл Карно при использовании водяного пара в качестве рабочего тела, имеет ряд существенных недостатков и мало эффективен.
За основной цикл в паротрубной установке (ПТУ) принят идеальный цикл Ренкина, в котором осуществляется полная конденсация пара, для увеличения давления питательной воды используется насос и, кроме того, применяется перегретый пар, что позволяет повысить среднеинтегральную температуру. Процессы нагрева и охлаждения рабочего тела осуществляются при Р1 = РMAX = Const и P2 = PMIN = Const.
В ПТУ химическая энергия топлива при его сжигании превращается во внутреннюю энергию продуктов сгорания, которая затем в виде тепла передаются воде и пару в котле 1 (процесс 4 – 5 – 6) и пароперегревателе 2 (процесс 6 – 1), полученный пар, направляется в паровую турбину 3 (процесс 1 – 2), где и происходит преобразование теплоты в работу, а затем в электрическую энергию в электрогенераторе 4, отработанный пар поступает в конденсатор 5 (процесс 2 – 3), где отдает тепло охлаждающей воде.
Полученный конденсат, насосом 6, отправляется в питательный бак 7, откуда нагнетательным насосом 8 сжимается до Р1 = РMAX (процесс 3 – 4) и через водонагреватель 9 подается в котел 1 (см. рис.9.1).
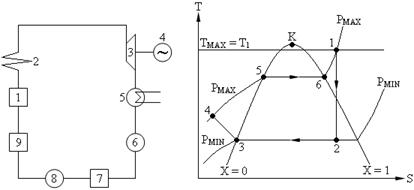
Рис.2.1.
Термический КПД цикла Ренкина определяется в виде отношения полезной работы цикла ко всей затраченной в цикле теплоты:
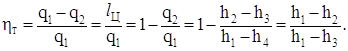(9.1)
Удельные расходы пара d0 и теплоты q0 определяются как:
(9.2)
(9.3)
Характеристики ПТУ, формулы (9.1 – 9.3), легко определяются с помощью h – S диаграммы.
Задачи для самостоятельного решения.
Задача № 2-1. Паросиловая установка работает по циклу Ренкина. Параметры начального состояния: Р1 = 30 бар, t1 = 300 °C. Давление в конденсаторе Р2 = 0,04 бар. Определить термический КПД, изобразить процесс в T – S координатах.
Задача № 2-2. Сравнить термический КПД идеальных циклов, работающих при одинаковых начальных и конечных давлениях Р1 = 200 бар и Р2 = 0,2 бар, если в одном случае используется пар влажный со степенью сухости Х = 0,9, в другом – пар сухой насыщенный и в третьем – пар с температурой t1 = 300 °C. Изобразить циклы в T – S координатах.
Задача № 2-3. Определить работу 1 кг пара в цикле Ренкина, если параметры пара: Р1 = 20 бар, t1 = 450 °C и Р2 = 0,04 бар. Изобразить цикл в P – V, T – S и h – S координатах.
Пример. Паросиловая установка работает по циклу Ренкина с начальными параметрами пара Р1 = 20 бар, t1 = 300 °C. Давление в конденсаторе P2 = 0,04 бар. Определить термический КПД цикла и построить его в T – S координатах.
Решение.
По диаграмме h – S находим энтальпии пара в начальном и конечном состояниях: h1 = 3019 кДж/кг; h2 = 2036 кДж/кг; h2' = 121 кДж/кг.
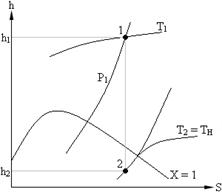
Рис. 2.2.
Термический КПД цикла определяется как:
ηT = (h1 – h2) /(h1 – h'2) = (3019 – 2036) /(3019 – 121) = 0,3392.
Задача №9-4. Выявить зависимость (и изобразить ее графически) термических КПД циклов Ренкина от начальных давления и температуры пара, если: 1) давление Р1 изменяется в пределах Р1 = 35 бар, Р'1 = 70 бар, Р"1 = 140 бар и Р'''1 = 280 бар, а температура во всех случаях одинакова, и равна t1 = 450 °C; 2) температура изменяется в пределах t1 = 400 °C, t'1 = 450 °C, t"1 = 500 °C и t'''1 = 600 °C, а давление во всех случаях одинаково и равно Р2 = 0,04 бар. Изобразить оба вариантов циклов в T – S координатах.
Задача №9-5. В паросиловой установке, работающей по циклу Ренкина, параметры пара соответствуют Р1 = 300 бар, t1 = 550 °C и Р2 = 1 бар. При давлении Р' = 70 бар вводится вторичный перегрев пара до температуры t'1 = 540 °C. Определить термический КПД двух установок и конечную степень сухости. Изобразить циклы в T – S координатах.
Задача № 1-6. В паросиловой установке, работающей при параметрах P1 = 110 бар; t1= 500 °C, Р2 = 0,04 бар, введен вторичный перегрев пара при Р = 30 бар до начальной температуры t' =500 °C. Определить термические КПД циклов с вторичным перегревом пара и без него. Изобразить циклы в T – S координатах.
Задача № 1-7. Пар при Р1 = 35 бар и t1= 435 °C поступает на турбину мощностью N = 4000 кВт установки, работающей по циклу Ренкина. Определить КПД цикла, удельный и часовой расход пара, если давление в конденсаторе Р2 = 1,2 бар. Изобразить цикл в T – S координатах.
Задача № 1-8. Пар при Р1 = 100 бар и t1= 550 °C поступает на турбину мощностью N = 100000 кВт, работающую по циклу Ренкина. Давление в конденсаторе Р2 = 0,04 бар. Определить удельный d кг/кВт × ч и часовой G кг/ч расходы пара, работу 1 кг пара, количество тепла, подводимое в котле и отводимое в конденсаторе за 1 ч, термический КПД цикла ηt и термический КПД цикла Карно для этого же интервала температур. Изобразить циклы в T – S координатах.
Задача № 1-9. Как изменится термический КПД установки, работающей по циклу Ренкина с параметрами пара Р1 = 20 бар и t1 = 300 °C, если пар подвергается дросселированию в первом случае до Р'1 = 16 бар, а во втором Р"2 = 12 бар. Конечное давление во всех случаях принять равным Р2 = 0,2 бар. Изобразить циклы в T – S координатах.
Прямые термодинамические циклы – циклы паротурбинных установок. Краткая теоретическая частьВ соответствии со вторым законом термодинамики, совершая обратный цикл Карно, т.е. затрачивая механическую работу, можно отнять некоторое количество теплоты от источника с низкой температурой и передать ее к источнику с более высокой температурой.
Холодильные циклы и установки на их основе чисто условно можно разделить по диапазону температур на две группы: умеренного охлаждения t > –100 °C и глубокого охлаждения t < –100 °C.
В процессах умеренного охлаждения для передачи "холода" используются промежуточные рабочие тела (аммиак, диоксид углерода, фреоны и другие), по которым циклы являются замкнутыми.
При производстве глубокого "холода" охлаждаемая среда сама служит рабочим телом, она отбирается из цикла для технических нужд, поэтому такие циклы являются незамкнутыми полностью по рабочему телу.
Установки умеренного охлаждения с использованием реальных рабочих тел, работающие по обратному циклу Карно, не нашли широкого распространения в силу ряда недостатков по их осуществлению.
Реальная паровая компрессионная холодильная установка отличается от идеальной (см. рис.3.1):
вместо детандера используется дроссель, процесс 3 – 4;
в компрессоре сжимается сухой и перегретый пар, процесс 1 – 2;
жидкость переохлаждается перед дросселем, процесс 3' – 3.
Холодильный коэффициент данной установки определяется по формулам (1.2) и (1.3):
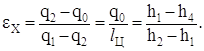(10.1)
Для увеличения холодопроизводительности Q0, а также получения "холода" при различных температурах, применяются многоступенчатые холодильные циклы и установки на их основе.
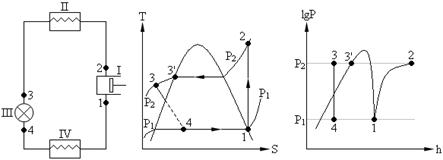
Рис. 3.1.
Процессы глубокого охлаждения применяются для достижения низких температур, получения сжиженных газов и последующего их разделения.
Для достижения низких температур газов используются процессы дросселирования и адиабатного расширения с отдачей внешней работы.
Особенности процессов глубокого охлаждения заключаются в том, что вначале газ сжимают в многоступенчатых компрессорных установках (T ≈ ≈ Const) процесс 1 – 2, затем его охлаждают (P = Const), процесс 2 – 3 и, наконец, дросселируют процесс 3 – 4. Полученный влажный пар сепарируют. Жидкость, как готовый продукт отводят (–y), а паровая фаза (низкопотенциальный поток), имеющая низкую температуру (при P1 = Const) (1 – у), используется для охлаждения высокопотенциального потока (P2 = = Const).
Принципиальная схема установки простого регенеративного цикла (цикла Линде) показана на рис. 3.2.
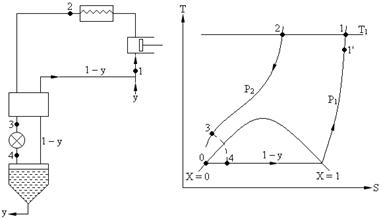
Рис. 3.2.
Расчет характеристик установки ведется на 1 кг газа, сжимаемого в компрессоре, т. к. некоторое количество сжиженного газа "у" отводится, то цикл по рабочему телу является незамкнутым. Кроме этого существуют потери "холода" в окружающую среду – q0 и потери тепла, связанные с наличием разности температур между встречными потоками газа, которые называются недорекуперацией – qHP. Вследствие этого удельная степень ожижения у' отличается от теоретической и рассчитывается по формуле:
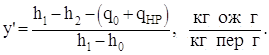(3.2)
Удельная энергия, затраченная на сжатие 1 кг газа, определяется по формуле:
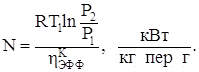(3.3)
Удельная энергия, приходящаяся на 1 кг жидкого газа, рассчитывается по формуле:
(3.4)
Модификация цикла Линде заключается в том, что часть сжатого газа "М", предварительно охлажденного, направляется в расширитель – детандер, где расширяется, одновременно понижая температуру, до начального давления Р1, а полученная при этом работа компенсирует часть затраты энергии на сжатие. Оставшаяся часть газа 1 – М продолжает охлаждаться и дросселируется, а затем ее сепарируют, а далее процессы аналогичны, как в цикле Линде. Принципиальные схемы установок и циклов Клода (цикла среднего давления) и цикла Гейландта (высокого давления) показаны на рис. 3.3.
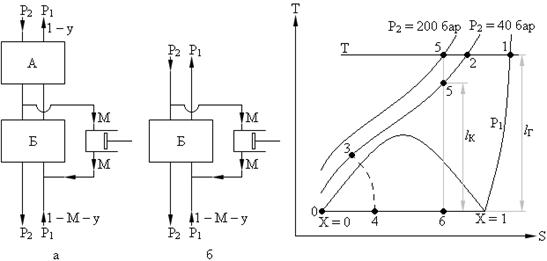
Рис. 3.3.
Схема: а) Клода, б) Гейландта; lК – работа в цикле Клода; lГ - работа в цикле Гейландта.
Удельная степень ожижения у' равна:
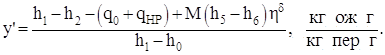(10.5)
А удельная энергия, затрачиваемая на сжатие, с учетом работы расширения, рассчитывается как:
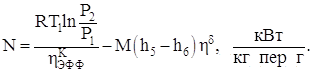(10.6)
Пример. Холодильная установка работает по циклу Карно, рабочее тело – пар аммиака. Параметры пара t1 = – 10 °C, t2 = 20 °C Х2 = 1 а Х3 = 0 (см. рис. 3.4). Определить холодопроизводительность аммиака, тепловую нагрузку конденсатора, работу, затраченную в цикле и холодильный коэффициент.
Решение. Параметры пара аммиака определяются по таблице 8 (см. приложение).
Холодопроизводительность установки:
q0 = h1 – h4 = r1(X1 – X4).
При t1 = – 10 °C и r1 = 1296,6 кДж/кг принимая процессы 1 – 2 и 3 – 4 адиабатным, имеем:
S2 = S1 = S' + (S"1 + S'1) X.
S'1 = 4,071 кДж/(кг×К), S"1 =8,944 кДж/(кг×К).
S2 = S"2 = 8,566 кДж/(кг×К).
X1 = (S"2 – S'1) /(S"1 – S'1) = (8,566 – 4,071) /(8,944 – 4,071) = 0,9224.
X4 = (S"2 – S'1) /(S"1 – S'1) = (4,516 – 4,017) /4,917 = 0,1015.
Следовательно:
q0 = 1296,6 × (0,9224 – 0,1015) = 1064,4 кДж/кг.
Тепловая нагрузка конденсатора:
q = h2 – h3 = r2 = 1186,9 кДж/кг.
Работа, затраченная в цикле:
l = q – q0 = 1186,9 – 1064,4 = 122,5 кДж/кг.
Холодильный коэффициент:
εХ = q0/l = 1064,4/122,5 = 8,69.
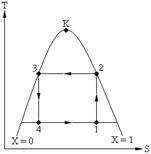
Рис. 3.4.
Задачи для самостоятельного решения.
Задача № 3.1. В схеме аммиачной холодильной установки, рис.10.4, расширительный цилиндр (процесс 3 – 4) заменен дроссельным вентилем, а остальные условия задачи сохраняются. Определить новое значение холодильного коэффициента, результаты сравнить.
Задача № 3.2. Аммиачная холодильная машина работает при температуре испарения t1 = – 10 °C. Пар из испарителя выходит сухим насыщенным. Температура конденсации пара t = 20 °C и она достигается в результате процесса дросселирования. Определить холодильный коэффициент и изобразить цикл установки в P – V и T – S координатах.
Задача № 3.3. Теоретическая мощность аммиачного компрессора холодильной установки N = 50 кВт. Температура испарения аммиака t1 = – 5 °C. Из компрессора пар выходит сухим насыщенным, при температуре t2 = 25 °C. температура жидкого аммиака понижается в дроссельном вентиле. Определить часовую холодопроизводительность 1 кг аммиака и всей установки.
Задача № 3.4. Определить холодильный коэффициент холодильной установки, работающей по влажному циклу Карно, если температура в испарителе – 30 °C, а в конденсаторе 27 °C.
Решение:
εХ = T0/(T – T0) = (273,15 – 30) /((273,15 – 27) – (273,15 – 30)) = 4,27.
Задача № 3.5. Вычислить теоретическую мощность, затрачиваемую аммиачной холодильной установкой, холодопроизводительностью Q0 = 17,4 кВт, работающей по циклу Карно если температура испарения – 19 °C, а конденсации 15 °C.
Задача № 3.6. Определить для углекислотной холодильной установки, работающей по влажному циклу, удельную холодопроизводительность, холодильный коэффициент, количество отводимой в конденсаторе теплоты, количество холодильного агента и мощность эл. двигателя, если температура испарения – 30 °C, а конденсации – 16 °C. Холодопроизводительность установки Q0 = 58,15 кВт.
Задача № 3.7. Определить количество получаемого в 1 ч жидкого воздуха и необходимую для этого затрату мощности при переработке 200 кг/ч воздуха, сжатого до Р2 = 200 атм. Установка работает по циклу Линде. Температура воздуха до и после компрессора 25 °C. Воздух дросселируется до Р1 = 1 атм потери холода в окружающую среду принять в размере 4,19 кДж на 1 нм3 воздуха (при нормальных условиях). Недорекуперация 5 °C. ηкэф = 0,62
Решение. Согласно рис.10.2 и формулам (10.2) – (10.4), пользуясь TS диаграммой для воздуха находим: h1 = 510 кДж/кг; h2 = 474 кДж/кг, h0 = 92,1 кДж/кг, qНР = CPΔt = 1,01 × 5 = 5,05 кДж/кг; q0 = 4, 19/ρH = 4, 19/1,29 = 3,25 кДж/кг.
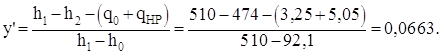
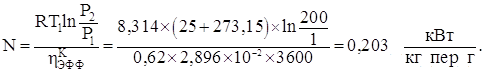
Задача № 3.8. Определить количество получаемого в 1 ч жидкого воздуха и необходимую для этого затрату энергии при переработке 200 кг/ч воздуха, сжатого до Р2 = 200 атм. Установка работает по циклу Гейландта. Температура воздуха до и после компрессора 25 °C. Воздух дросселируется до Р1 = 1 атм. В детандер отводится 80% воздуха (М = 0,8). Недорекуперация 5 °C. Потери холода принять q0 = 0,93 кВт. Работа, получаемая в детандере составляет 50% от теоретической (при S = Const; ηкэф = 0,65; ηдэф = 0,7).
0 комментариев