Введение
1. Статистические ряды распределения, их значение и применение в статистике
2. Расчетная часть
3. Аналитическая часть
Заключение
Список использованной литературы
Введение
С незапамятных времен человечество осуществляло учет многих сопутствующих его жизнедеятельности явлений и предметов и связанные с ним вычисления. Люди получали разносторонние, хотя и различающиеся полнотой на различных этапах общественного развития. Данные, учитывавшиеся повседневно в процессе принятия хозяйственных решений, а в обобщенном виде и на государственном уровне при определении русла экономической и социальной политики и характера внешнеполитической деятельности.
Руководствуясь соображениями зависимости благосостояния нации от величины создаваемого полезного продукта, интересов стратегической безопасности государств и народов от численности взрослого мужского населения, доходов казны от размера налогооблагаемых ресурсов и т. д., издавна отчетливо осознавалась и реализовывалась в форме различных учетных акций.
С учетом достижений экономической науки стал возможен расчет показателей, обобщенно характеризующих результаты воспроизводственного процесса на уровне общества: совокупного общественного продукта, национального дохода, валового национального продукта.
Всю перечисленную информацию в постоянно возрастающих объемах предоставляет обществу статистика, являющаяся необходимо принадлежностью государственного аппарата. Статистические данные, таким образом, способны сказать языком статистических показателей о многом в весьма яркой и убедительной форме.
Для статистического анализа данных в своей работе я использовала программу Excel (расчет формул и построение графиков).
Статистические ряды распределения, их значение и применение в статистике
В результате обработки и систематизации первичных данных статистического наблюдения получают группировки, называемые рядами распределения. В них известна численность единиц наблюдения в группах. Представленная в абсолютном и относительном выражении.
Статистический ряд распределения представляет собой упорядоченное распределение единиц изучаемой совокупности на группы по определенному варьирующему признаку. Он характеризует состав (структуру) изучаемого явления, позволяет судить об однородности совокупности, закономерности распределения и границах варьирования единиц совокупности.
Статистические ряды подразделяются на:
Атрибутивные – это ряды, построенные по атрибутивным признакам, в порядке возрастания или убывания наблюдаемых знаний.
То есть качественным признакам, не имеющим числового выражения и характеризующим свойство, качество изучаемого социально-экономического явления.
Атрибутивные ряды распределения характеризуют состав совокупности по тем или иным существенным признакам.
Взятые за несколько периодов, эти данные позволяют исследовать изменение структуры.
Число групп атрибутивного ряда распределения адекватно числу градаций. Разновидностей атрибутивного признака.
Пример атрибутивного ряда распределения приведен в таблице 1.
Таблица 1. Распределение студентов 1-го курса по успеваемости
| Успеваемость | Число студентов, чел | Удельный вес в общей численности студентов. % |
| Успевают | 46 | 92 |
| Не успевают | 4 | 8 |
| Итого: | 50 | 100 |
Элементами данного ряда распределения являются градации атрибутивного признака «Успеваемость» («успевают» - «не успевают») и численность каждой группы в абсолютном (человек) и относительном (%) выражении.
Студентов, сдавших экзамен по дисциплине, было 46 человек. Их удельный вес составил 92%.
Вариационные – это ряды, построенные по количественному признаку.
Вариационные ряды распределения состоят из двух элементов: вариантов и частот:
- варианты – это числовые значения количественного признака в вариационном ряду распределения. Они могут быть положительными и отрицательными, абсолютными и относительными. Так, при группировке предприятий по результатам хозяйственной деятельности варианты положительные – это прибыль, а отрицательные числа – это убыток.
- частоты – это численности отдельных вариантов или каждой группы вариационного ряда, т.е. это числа, показывающие, как часто встречаются те или иные варианты в ряду распределения. Сумма всех частот называется объемом совокупности и определяется числом элементов всей совокупности.
- частости – это частоты, выраженные в виде относительных величин (долях единиц или процентах). Сумма частостей равна единице или 100%. Замена частот частостями позволяет сопоставлять вариационные ряды с разным числом наблюдений.
Вариационные ряды в зависимости от характера вариации подразделяются на дискретные и интервальные.
Дискретный вариационный ряд распределения – это ряд, в котором группы составлены по признаку, изменяющемуся дискретно и принимающему только целые значения.
Пример дискретного вариационного ряда распределения приведен в таблице 2.
Таблица 2. Распределение студентов по экзаменационному баллу
| Экзаменационный балл | Число студентов, чел. | Удельный вес студентов, в % к итогу |
| 1 | 2 | 3 |
| 5 | 16 | 32 |
| 4 | 23 | 46 |
| 3 | 7 | 14 |
| 2 | 4 | 8 |
| Итого: | 50 | 100 |
В гр. 1 таблицы 2 представлены варианты дискретного вариационного ряда. В гр. 2 – частоты, а в гр. 3 – частости. В случае непрерывной вариации величина признака у единиц совокупности может принимать в определенным пределах любые значения. Отличающиеся друг от друга на сколь угодно малую величину.
Интервальный вариационный ряд распределения – это ряд, в котором группировочный признак, составляющий основание группировки, может принимать в определенном интервале любые значения, в том числе и дробные.
Интервальный ряд распределения целесообразно строить, прежде всего, при непрерывной вариации признака, а также, если дискретная вариация проявляется в широких пределах, т.е. число вариантов дискретного признака достаточно велико.
Правила и принципы построения интервальных рядов распределения аналогичны правилам и принципам построения статистических группировок. В случае, если интервальный вариационный ряд распределения построен с равными интервалами, частоты позволяют судить о степени заполнения интервала единицами совокупности. При построении неравных интервалов нельзя получить информацию о степени заполнения каждого интервала. С целью проведения сравнительного анализа заполненности интервалов определяется показатель, характеризующий плотность распределения. Это отношение числа единиц совокупности к ширине интервала.
Пример интервального вариационного рада распределения приведен в таблице 3.
Таблица 3. Распределение строительных фирм региона по среднесписочной численности работающих*
| Численность работающих, чел. | Число строительных фирм | Удельный вес, в % к итогу |
| 100 – 200 | 12 | 15,00 |
| 200 – 300 | 18 | 22,50 |
| 300 – 400 | 25 | 31,25 |
| 400 – 500 | 14 | 17,50 |
| 500 – 600 | 11 | 13,75 |
| Итого: | 80 | 100,00 |
* - Цифры условные
Представленный ряд распределения является интервальным, в основании образования групп которого лежит непрерывный признак.
Анализ рядов распределения можно для наглядности проводить на основе их графического изображения. Для этой цели строят полигон, гистограмму, огиву и кумуляту распределения.
Расчетная часть задания № 5
Имеются выборочные данные (выборка 5%-я механическая) о среднегодовой стоимости основных производственных фондов и выпуске продукции предприятий отрасли экономики за отчетный период.
Таблица 4. Исходные данные
| № п/п | Среднегодовая стоимость ОПФ, млн. руб. | Выпуск продукции, млн. руб. |
| 1 | 27 | 21 |
| 2 | 46 | 27 |
| 3 | 33 | 41 |
| 4 | 35 | 30 |
| 5 | 41 | 47 |
| 6 | 42 | 42 |
| 7 | 53 | 34 |
| 8 | 55 | 57 |
| 9 | 60 | 46 |
| 10 | 46 | 48 |
| 11 | 39 | 45 |
| 12 | 45 | 43 |
| 13 | 57 | 48 |
| 14 | 56 | 60 |
| 15 | 36 | 35 |
| 16 | 47 | 40 |
| 17 | 20 | 24 |
| 18 | 29 | 36 |
| 19 | 26 | 19 |
| 20 | 49 | 39 |
| 21 | 38 | 35 |
| 22 | 37 | 34 |
| 23 | 56 | 61 |
| 24 | 49 | 50 |
| 25 | 37 | 38 |
| 26 | 33 | 30 |
| 27 | 55 | 51 |
| 28 | 44 | 46 |
| 29 | 41 | 38 |
| 30 | 28 | 35 |
По исходным данным:
1. Постройте статистический ряд распределения предприятий по среднегодовой стоимости основных производственных фондов, образовав четыре группы предприятий с равными интервалами, охарактеризовав их числом предприятий и удельным весом предприятий.
2. Рассчитайте обобщающие показатели ряда распределения:
а) среднегодовую стоимость основных производственных фондов, взвешивая значения признака по абсолютной численности предприятий и их удельному весу;
б) моду и медиану;
в) постройте графики ряда распределения и определите на них значение моды и медианы.
Решение:
1. Сначала определяем длину интервала по формуле:
е=(хmax – xmin)/k,
где k – число групп в группировке (из условия k=4),
хmax и xmin–максимальное и минимальное значения ряда распределения,
е=(60 – 20)/4=10 млн. руб.
Затем определим нижнюю и верхнюю интервальные границы для каждой группы:
| Номер группы | нижняя граница | верхняя граница |
| I | 20 | 30 |
| II | 30 | 40 |
| III | 40 | 50 |
| IV | 50 | 60 |
Составим рабочую таблицу 5, куда сведем исходные данные:
Таблица 5. Рабочая таблица
| Группы пред-ий по среднегодовой стоимости ОПФ, млн. руб. | № предпри-ятия | Среднегодовая стоимость ОПФ, млн. руб. | Выпуск продукции, млн. руб. |
| 1 | 2 | 3 | 4 |
| 20 – 30 | 1 | 27 | 21 |
| 17 | 20 | 24 | |
| 18 | 29 | 36 | |
| 19 | 26 | 19 | |
| 30 | 28 | 35 | |
| 30 – 40 | 3 | 33 | 41 |
| 4 | 35 | 30 | |
| 11 | 39 | 45 | |
| 15 | 36 | 35 | |
| 21 | 38 | 35 | |
| 22 | 37 | 34 | |
| 25 | 37 | 38 | |
| 26 | 33 | 30 | |
| 40 – 50 | 2 | 46 | 27 |
| 5 | 41 | 47 | |
| 6 | 42 | 42 | |
| 10 | 46 | 48 | |
| 12 | 45 | 43 | |
| 16 | 47 | 40 | |
| 20 | 49 | 39 | |
| 24 | 49 | 50 | |
| 28 | 44 | 46 | |
| 29 | 41 | 38 | |
| 50 – 60 | 7 | 53 | 34 |
| 8 | 55 | 57 | |
| 9 | 60 | 46 | |
| 13 | 57 | 48 | |
| 14 | 56 | 60 | |
| 23 | 56 | 61 | |
| 27 | 55 | 51 |
Рассчитаем характеристику ряда распределения по удельному весу предприятий по формуле:
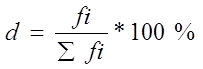
где d - удельный вес предприятия;
fi - кол-во предприятий в группе;
fi - общее кол-во предприятий.
Подставляем данные в формулы. Полученные результаты заносим в итоговую таблицу 6.
Все формулы и расчеты таблицы 6 введены в программе Excel и даны в Приложении 1.
Таблица 6. Распределения предприятий по среднегодовой стоимости основных производственных фондов
| Номер группы | Группы предприятий по среднегодовой стоимости ОПФ, млн. руб. | Предприятия | |
| в абсолютном выражении | в относительных единицах, % | ||
| I | 20 – 30 | 5 | 16,7 |
| II | 30 – 40 | 8 | 26,7 |
| III | 40 – 50 | 10 | 33,3 |
| IV | 50 – 60 | 7 | 23,3 |
| Итого: | 30 | 100 | |
Данная группировка показывает, что у наибольшей части данных предприятий (33,3%) среднегодовая стоимость основных производственных фондов составляет от 40 до 50 млн. руб.
2. а) Рассчитаем среднегодовую стоимость основных производственных фондов по формуле средней арифметической взвешенной, взвешивая значения по абсолютной численности предприятий:
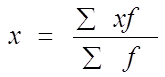
и по удельному весу:
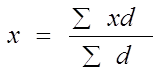
Для расчета средней из интервального ряда необходимо выразить варианты одним (дискретным) числом, это средняя арифметическая простая из верхнего и нижнего значений интервала:
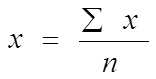
Подставляем данные в формулы. Полученные результаты занесем в таблицу 7.
Все формулы и расчеты таблицы 7 введены в программе Excel и даны в Приложении 1.
Таблица 7. Расчет среднегодовой стоимости ОПФ
| № группы | Среднегодовая стоимость ОПФ, x | Число предпри-ятий, f | Удельный вес предприятий в %, d | Середина интервала, х’ | xf | xd |
| I | 20 – 30 | 5 | 16,7 | 25 | 125 | 4,167 |
| II | 30 – 40 | 8 | 26,7 | 35 | 280 | 9,333 |
| III | 40 – 50 | 10 | 33,3 | 45 | 450 | 15,000 |
| IV | 50 – 60 | 7 | 23,3 | 55 | 385 | 12,833 |
| Итого: | 30 | 100 | – | 1240 | 41,333 | |
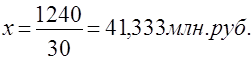
Показатели средних равны, что доказывает правильность расчетов. Среднегодовая стоимость ОПФ равна 41,333 млн. руб.
б) Рассчитаем моду и медиану данного ряда.
Мода – это значение признака, наиболее часто встречающееся в изучаемой совокупности. Для интервальных вариационных рядов распределения мода рассчитывается по формуле:
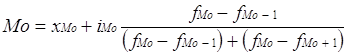
где xMo - нижняя граница модального интервала;
iMo - величина модального интервала;
fMo - частота модального интервала;
fMo-1 - частота интервала, предшествующего модальному;
fMo+1 - частота интервала, следующего за модальным.
Первоначально по наибольшей частоте признака определим модальный интервал. Наибольшее число предприятий – 10 – среднегодовая стоимость основных производственных фондов в интервале 40 – 50 млн. руб., который и является модальным.
Подставляем данные в формулу.
![]()
Из расчета видно, что модальным значением стоимости ОПФ предприятий является стоимость равная 44 млн. руб.
Медиана – это вариант, расположенный в середине упорядоченного вариационного ряда, делящий его на две равные части. Для интервальных вариационных рядов медиана рассчитывается по формуле:
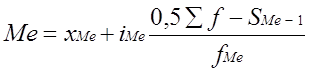
где xMе - нижняя граница медианного интервала;
iMе - величина медианного интервала;
f - сумма частот ряда;
SMе-1 - сумма накопленных частот ряда, предшествующих медианному интервалу;
fMе - частота медианного интервала.
Определяем медианный интервал, в котором находится порядковый номер медианы. Для этого подсчитаем сумму частот накопленным итогом до числа, превышающего половину объема совокупности (30/2 = 15). Полученные данные заносим в расчетную таблицу 8.
Таблица 8. Расчет медианны
| № группы | Среднегодовая стоимость основных производственных фондов, млн. руб. | Число предприятий | Сумма накопленных частот |
| I | 20 – 30 | 5 | 5 |
| II | 30 – 40 | 8 | 13 |
| III | 40 – 50 | 10 | 23 |
| IV | 50 – 60 | 7 | 30 |
| Итого: | 30 | - | |
В графе «Сумма накопленных частот» значение 23 соответствует интервалу 40 – 50. Это и есть медианный интервал, в котором находится медиана.
Подставляем данные в формулу.
![]()
Из расчета видно, что у половины предприятий среднегодовая стоимость основных производственных фондов до 42 млн. руб., а у другой половина – выше этой суммы.
в) Построим графики данного ряда распределения по полученным данным:
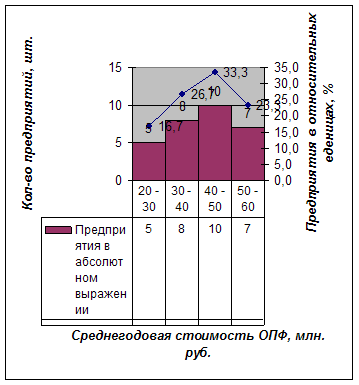
Рис. 1. Гистограмма распределение предприятий по среднегодовой стоимости ОПФ
- Мода
- Медиана
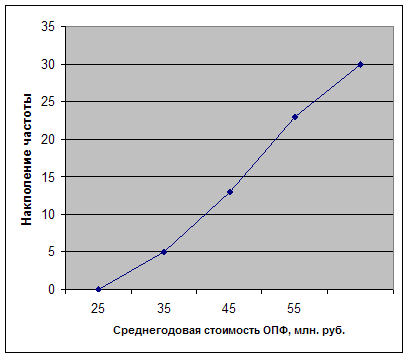
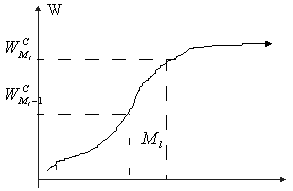
Рис. 2. Кумулята распределения предприятий по среднегодовой стоимости ОПФ
- Медиана
Аналитическая часть
Для расчета аналитической части своей работы я воспользовалась данными «Российского статистического ежегодника».
Имеются данные о среднегодовой стоимости основных производственных фондов (ОПФ) и выпуске продукции отраслей промышленности за 2002г.
Таблица 9. Исходные данные
| Промышленность | Среднегодовая стоимость ОПФ, тыс. млн. руб. | Объем производ. продукции, млн. руб. |
| Электроэнергетика | 1040 | 520 |
| Топливная | 916 | 990 |
| Черная металлургия | 299 | 395 |
| Цветная металлургия | 550 | 620 |
| Химическая и нефтехимическая | 341 | 347 |
| Машиностроение и металлообработка | 806 | 1014 |
| Лесная, деревообрабатывающая и целлюлозно-бумажная | 129 | 220 |
| Промышленность строительных материалов | 102 | 153 |
| Легкая | 50 | 80 |
| Пищевая | 275 | 687 |
| Нефтедобывающая | 67 | 65 |
| Нефтеперерабатывающая | 104 | 140 |
| Газовая | 50 | 112 |
| Угольная | 90 | 78 |
По исходным данным:
1. Постройте статистический ряд распределения отраслей по среднегодовой стоимости ОПФ, образовав четыре группы отраслей с равными интервалами, охарактеризовав их числом отраслей и удельным весом отраслей.
2. Рассчитайте обобщающие показатели ряда распределения:
а) среднегодовую стоимость ОПФ, взвешивая значения признака по абсолютной численности отраслей и их удельному весу;
б) моду и медиану;
в) постройте графики ряда распределения и определите на них значение моды и медианы.
Решение:
1. Сначала определяем длину интервала по формуле:
е=(хmax – xmin)/k,
где k – число групп в группировке (из условия k=4),
хmax и xmin–максимальное и минимальное значения ряда распределения,
е=(1040 – 50)/4=247,5 млн. руб.
Затем определим нижнюю и верхнюю интервальные границы для каждой группы:
| Номер группы | нижняя граница | верхняя граница |
| I | 50 | 297,5 |
| II | 297,5 | 545 |
| III | 545 | 792,5 |
| IV | 792,5 | 1040 |
Составим рабочую таблицу 10, куда сведем исходные данные таблицы 9:
Таблица 10. Рабочая таблица
| Группы отраслей промышленности по среднегодовой стоимости ОПФ, тыс. млн. руб. | Промышленность | Среднегодовая стоимость ОПФ, млн. руб. | Объем производ. продукции, млн. руб. |
| 50 – 297,5 | Легкая | 50 | 80 |
| Газовая | 50 | 112 | |
| Нефтедобывающая | 67 | 65 | |
| Угольная | 90 | 78 | |
| Промышленность строительных материалов | 102 | 153 | |
| Нефтеперерабатывающая | 104 | 140 | |
| Лесная, деревообрабатывающая и целлюлозно-бумажная | 129 | 220 | |
| Пищевая | 275 | 687 | |
| 297,5 – 545 | Черная металлургия | 299 | 395 |
| Химическая и нефтехимическая | 341 | 347 | |
| 545 – 792,5 | Цветная металлургия | 550 | 620 |
| 792,5 – 1040 | Машиностроение и металлообработка | 806 | 1014 |
| Топливная | 916 | 990 | |
| Электроэнергетика | 1041 | 520 |
Рассчитаем характеристику ряда распределения по удельному весу отраслей по формуле:
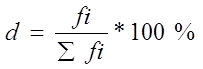
где d - удельный вес предприятия;
fi - кол-во предприятий в группе;
fi - общее кол-во предприятий.
Подставляем данные в формулу. Полученные результаты занесем в итоговую таблицу 11.
Все формулы и расчеты таблицы 11 введены в программе Excel и даны в Приложении 2.
Таблица 11. Распределения отраслей промышленности по среднегодовой стоимости ОПФ
| Номер группы | Группы отраслей промышленности по среднегодовой стоимости ОПФ, тыс. млн. руб. | Регионы | |
| в абсолютном выражении | в относительных единицах, % | ||
| I | 50 - 297,5 | 8 | 57,1 |
| II | 297,5 - 545 | 2 | 14,3 |
| III | 545 - 792,5 | 1 | 7,1 |
| IV | 792,5 - 1040 | 3 | 21,4 |
| Итого: | 14 | 100 | |
Данная группировка показывает, что у наибольшей части отраслей промышленности (57,1%) среднегодовая стоимость основных производственных фондов составляет от 50 до 297,5 млн. руб.
3. а) Рассчитаем среднегодовую стоимость основных производственных фондов по формуле средней арифметической взвешенной, взвешивая значения по абсолютной численности отраслей:
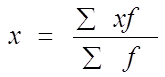
и по удельному весу:
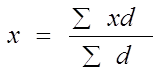
Для расчета средней из интервального ряда необходимо выразить варианты одним (дискретным) числом, это средняя арифметическая простая из верхнего и нижнего значений интервала:
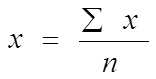
Подставляем данные в формулы. Полученные результаты занесем в таблицу 12.
Все формулы и расчеты таблицы 12 введены в программе Excel и даны в Приложении 2.
Таблица 12. Расчет среднегодовой стоимости ОПФ
| № группы | Среднегодовая стоимость ОПФ, x | Число регионов, f | Удельный вес регионов в %, d | Середина интервала, х’ | xf | xd |
| I | 50 - 297,5 | 8 | 57,1 | 174 | 1390,00 | 99,29 |
| II | 297,5 - 545 | 2 | 14,3 | 421 | 842,50 | 60,18 |
| III | 545 - 792,5 | 1 | 7,1 | 669 | 668,75 | 47,77 |
| IV | 792,5 - 1040 | 3 | 21,4 | 916 | 2748,75 | 196,34 |
| Итого: | 14 | 100 | - | 5650 | 403,57 | |
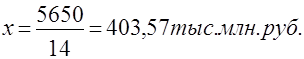
Показатели средних равны, что доказывает правильность расчетов. Среднегодовая стоимость ОПФ равна 403 тыс. 57 млн. руб.
б) Рассчитаем моду и медиану данного ряда
Мода – это значение признака, наиболее часто встречающееся в изучаемой совокупности. Для интервальных вариационных рядов распределения мода рассчитывается по формуле:
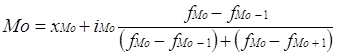
где xMo - нижняя граница модального интервала;
iMo - величина модального интервала;
fMo - частота модального интервала;
fMo-1 - частота интервала, предшествующего модальному;
fMo+1 - частота интервала, следующего за модальным.
Первоначально по наибольшей частоте признака определим модальный интервал. Наибольшее число отраслей – 8 – среднегодовая стоимость ОПФ в интервале 50 – 297,5 млн. руб., который и является модальным.
Подставляем данные в формулу.
![]()
Из расчета видно, что модальным значением стоимости ОПФ предприятий является стоимость равная 160 тыс. млн. руб.
Медиана – это вариант, расположенный в середине упорядоченного вариационного ряда, делящий его на две равные части. Для интервальных вариационных рядов медиана рассчитывается по формуле:
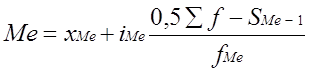
где xMе - нижняя граница медианного интервала;
iMе - величина медианного интервала;
f - сумма частот ряда;
SMе-1 - сумма накопленных частот ряда, предшествующих медианному интервалу;
fMе - частота медианного интервала.
Определяем медианный интервал, в котором находится порядковый номер медианы. Для этого подсчитаем сумму частот накопленным итогом до числа, превышающего половину объема совокупности (14/2 = 7). Полученные данные заносим в расчетную таблицу 13.
Таблица 13. Расчет медианны
| № группы | Среднегодовая стоимость основных производственных фондов, млн. руб. | Число предприятий | Сумма накопленных частот |
| I | 50 - 297,5 | 8 | 8 |
| II | 297,5 - 545 | 2 | 10 |
| III | 545 - 792,5 | 1 | 11 |
| IV | 792,5 - 1040 | 3 | 14 |
| Итого: | 14 | - | |
В графе «Сумма накопленных частот» значение 8 соответствует интервалу 50 – 297,5. Это и есть медианный интервал, в котором находится медиана.
Подставляем данные в формулу.
![]()
Из расчета видно, что у половины предприятий среднегодовая стоимость основных производственных фондов до 267 тыс. млн. руб., а у другой половина – выше этой суммы.
в) Построим графики данного ряда распределения по полученным данным:
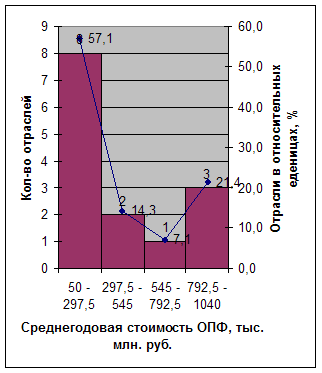
Рис. 3. Гистограмма распределение отраслей промышленности по среднегодовой стоимости ОПФ
- Мода
- Медиана
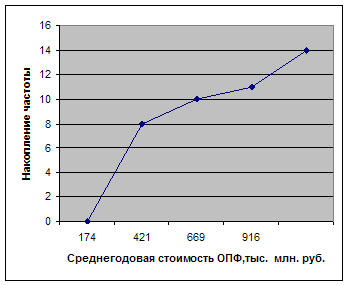
Рис. 4. Кумулята распределения отраслей промышленности по среднегодовой стоимости ОПФ
- Медиана
Заключение
Возрастающий интерес к статистике вызван современным этапом развития экономики в стране, формирования рыночных отношений. Это требует глубоких экономических знаний в области сбора, обработки и анализа экономической информации.
Организация единой централизованной системы хозяйственно-правовой статистики в Российской Федерации дала бы возможность выявить наиболее уязвимые места в правовом регулировании, экономическом обороте и экономике страны в целом, содействовала бы предотвращению хозяйственных правонарушений и преступлений.
Статистическая грамотность является неотъемлемой составной частью профессиональной подготовки каждого экономиста, финансиста, социолога, политолога, а также любого специалиста, имеющего дело с анализом массовых явлений, будь то социально-общественные, экономические, технические, научные и другие явления.
Список используемой литературы
1. Практикум по статистике: Учебное пособие для вузов / Под ред. В.М. Симчеры / ВЗВЭИ. – М.: ЗАО «Финстатинформ», 1999 – 259 с.
2. Российский статистический ежегодник 2002: Статистический сборник / Госкомстат России. – М.: 2002г. – 690 с.
3. Социально-экономическая статистика / Под ред. Г.Л. Громыко. – М.: Издательство МГУ, 1989. – 398 с.
4. Теория статистики: Учебное пособие для вузов. – М.: Аудит, ЮНИТИ, 1998. – 247 с.
5. Сайты в Интернете: http://www.gks.ru и http://www.infostat.ru
Похожие работы
... публикаций статистической информации позволяет лучше видеть положение дел на местах, в отдельных регионах, сосредоточить внимание на недостатках и упущениях для их устранения. Возвращение статистике широкого общественного предназначения определяет главные направления ее развития: совершенствование анализа статистической информации, упорядочение отчетности, обеспечение ее достоверности. Главным ...
... 21 2,0 2,8 3,8 22 2,0 2,8 3,7 23 2,0 2,8 3,7 24 2,0 2,7 3,7 25 2,0 2,7 3,7 26 2,0 2,7 3,7 27 2,0 2,7 3,6 28 2,0 2,7 3,6 29 2,0 2,7 3,6 30 2,0 2,7 3,6 ¥ 1,9 2,5 3,3 ТЕСТЫ к практическому занятию по теме «Средние величины, оценка разнообразия признака в вариационном ряду. Оценка достоверности» 1. Средние величины применяются для характеристики ...
... случайной величиной и все статистические выводы приходится делать, опираясь только на результаты «пробных» испытаний. Именно такие модели в основном рассматриваются в математической статистике. В математической статистике употребляют также понятие параметрической и непараметрической модели. Параметрическая модель возникает тогда, когда нам известен вид функции распределения наблюдаемого признака, ...
... вес, объем, урожайность. Абсолютная шкала является безразмерной шкалой отношений. Тема 2. Вариационные ряды. Пример 1. Приведем оценки 45 студентов по курсу статистика в порядке сдачи экзамена: 5 3 3 4 2 4 4 3 5 4 4 5 5 4 4 3 3 3 2 5 5 4 4 4 3 4 3 4 5 4 4 4 4 3 3 4 3 4 3 2 3 2 3 3 3 При таком представлении информации трудно делать какие-либо выводы об успеваемости. Произведем группировку данным ...

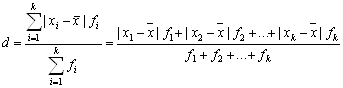
0 комментариев