Финансовые функции и рекурсия

Министерство образования РФ

Тульский государственный педагогический университет

имени Л.Н. Толстого

Кафедра информатики

Дипломная работа

"Финансовые функции" и рекурсия

Выполнил:

Научный руководитель:

Тула-2000

План

Введение. 4

Динамика вклада. 7

Задача о величине вклада. 7

Задача о величине вклада после снятия денег в конце каждого периода 11

Задача о величине вклада после внесения (снятия) денег в конце или начале каждого периода. 13

Задача о изменяющихся процентных ставках. 15

Задача о изменяющихся процентных ставках и величинах снимаемых денег 16

Дисконтирование. Инвестиции. Консолидирование. 19

Задача о дисконтировании. 19

Задача о инвестировании проекта. 21

Задача о консолидировании платежей. 23

Платежи. 25

Задача о равных платежах в конце каждого периода. 25

Задача о платежах с одинаковой современной стоимостью.. 30

Задача о платежах на проценты.. 31

Разные задачи. 34

Задача о величине процентной ставки. 34

Задача о величине процентной ставки 2. 36

Задача о количестве периодов для расчета заемщика с банком.. 38

Задача о суммарной способности к кредитованию.. 41

Задача о минимальном количестве банков. 42

Задача о изменении величины суммарного кредитования. 43

Заключение. 50

Литература. 51

Введение

В электронные таблицы Excel, систему управления базами данных Access, язык программирования Visual Basic и многие другие современные компьютерные технологии встроены так называемые “финансовые функции”: fv(), pv(), pmt(), ppmt(), ipmt(), rate(), nper() и т.д. В повседневной жизни с задачами, в которых они могут быть использованы, приходится сталкиваться достаточно часто. Это заставляет преподавателей информатики педагогических вузов не только знакомить студентов различных специальностей с синтаксисом и семантикой этих функций, но и уделять особое внимание поиску новых методик и технологий обучения, ориентированных на прочное усвоение соответствующих знаний. И здесь на помощь может прийти рекурсия, с помощью которой строятся лаконичные и легко понимаемые алгоритмы, а затем и соответствующие информационные модели в виде рекурсивных программ на том или ином языке программирования [9, 10]. И что особенно важно, набор упомянутых финансовых функций и рекурсивные алгоритмы их вычисления могут служить весьма подходящим фоновым материалом для начального освоения студентами рекурсии как достаточно общего и эффективного метода решения практических задач.

Заметим, что вычисление значений финансовых функций с помощью электронных таблиц Excel или других пакетов прикладных программ можно признать целесообразным лишь при уже полностью сформированном понимании их синтаксиса и семантики. Но при первом знакомстве с этими и другими функциями рекурсивный подход в полной мере демонстрирует все свои дидактические преимущества по сравнению с простым описанием функций и решением по ним соответствующих прикладных задач. Он дает возможность не только всесторонне понять содержание излагаемого материала, но сделать это быстро и эффективно. И что особенно важно, полученные знания становятся достоянием долговременной памяти. Последний вывод убедительно подтверждается результатами проверочной работы, проведенной в двух группах студентов через год после ознакомления их с финансовыми функциями. Результаты эти оказались и удивительными, и убедительными. Более 36 процентов студентов, которым материал преподносился традиционно, с предъявленным заданием не справились. В то же самое время в группе, осваивавшей этот же материал с использованием рекурсии, с заданием не справились лишь 12 процентов студентов (3 человека). Столь разительное различие в уровне усвоения знаний в экспериментальной и контрольной группах заставляет нас по-новому оценить дидактические возможности рекурсии и осознать её роль и место в построении современного курса информатики в педагогических вузах. И эта роль, по-видимому, будет возрастать вместе с дальнейшим развитием компьютерной техники и программного обеспечения. В связи с этим главной задачей данной дипломной работы является разработка методик решения финансовых задач рекурсивными методами и их практическая реализация в виде обучающей программы (Web-узла) по данной теме.

При отборе материала для первоначального знакомства студентов и учащихся с рекурсивными методами решения прикладных задач, ориентированных на экономические специальности, существенную роль играют два фактора: наличие экономического содержания в этих задачах и прозрачность свойств рекурсивности рассматриваемых в них объектов. И то, и другое в полной мере может быть обеспечено рекурсивной реализацией финансовых функций.

Большой выбор содержательных задач, решаемых финансовыми функциями, можно встретить в сфере банковской деятельности [1,3-6]. Причем возникают они здесь на обслуживании всего лишь двух операций. Банк, являясь финансовым посредником между вкладчиками и заемщиками (рис.1), с одной стороны, принимает деньги и платит по ним проценты, а с другой стороны, дает кредиты и получает за них проценты. Разность между той суммой, которую получает банк от заемщиков по процентам за конкретный период, и той, которую он платит вкладчикам по процентам за этот же период, и составляет прибыль банка. Как говорил американский писатель-сатирик Генри Уилер Шоу [2, с.30] “Банковский процент не знает ни отдыха, ни богослужений, он работает и по ночам, и в воскресенье, и даже в дождливые дни”.

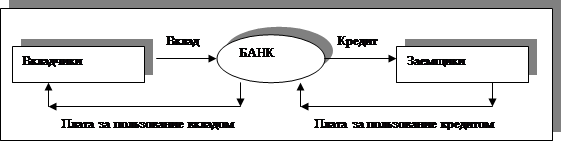Рис.1. Банк как финансовый посредник между вкладчиками и заемщиками

В рассматриваемой ниже серии задач везде речь идет об обычных вкладах и сложных процентах, а решения оформлены в виде рекурсивных программ-функций на языке программирования вычислительной среды Mathcad. Все они делятся на три категории: прямые рекурсивные аналоги, частные случаи и обобщения встроенных в Excel финансовых функций. Для первой категории функций и их аргументов используются стандартные обозначения. В иных ситуациях обозначения произвольны. Наличие почти во всех задачах несложно выводимой при определенных навыках, но обычно громоздкой, конечной формулы-решения позволяет на контрольных примерах легко проверить правильность составленных для них рекурсивных программ. Отметим, что все приведенные программы, благодаря рекурсивности, весьма просты и для их написания не требуется знания соответствующих конечных формул. В дополнении к данной работе дается краткое описание Mathcad и программы Microsoft FrontPage 2000, с помощью которой был создан Web-узел.

Динамика вклада

Начнем упомянутую серию задач с рассмотрения простой и многим знакомой житейской проблемы хранения денег в банке.

Задача о величине вклада

Вкладчик положил в банк сумму в sum денежных единиц под p процентов за один период времени (год, месяц, неделя и т.д.). Составить программу-функцию, возвращающую величину вклада по истечении n периодов времени (n = 1, 2, …).

Решение. Пусть invest(sum,p,n) - искомая функция. Вычисления значений invest() можно проводить по известной формуле:

invest(sum,p,n) = sum×(1+p/100) n.

Однако в учебных целях нас будет интересовать рекурсивный вариант алгоритма решения задачи. Её параметризация реализована в постановке. Рекурсию будем осуществлять по параметру n. База рекурсии очевидна. В самом деле, если вклад положен на хранение и взят сразу, то есть до истечения первого периода времени начисления процентов, то возврату подлежит начальная сумма вклада - sum. Далее, декомпозиция может быть реализована исходя из следующего факта. Положить некоторую сумму в банк на n периодов – это то же самое, что положить эту сумму на n – 1 период, взять и снова положить на 1 период. Соответствующий вариант программы-функции решения задачи выглядит так:

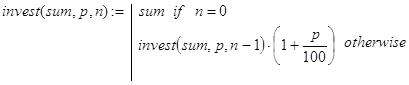 (1)

Реализуя декомпозицию иным способом, получим другой вариант рекурсивной программы (1). Например, сделаем это исходя из такого факта. Положить некоторую сумму в банк на n периодов – это то же самое, что положить эту сумму на 1 период, взять и снова положить на n-1 период. Соответствующая программа-функция выглядит так:

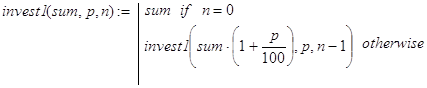 (2)

В данной и подобной ей задачах указанные декомпозиционные посылки программно реализуются приблизительно с равной степенью сложности и, тем самым, обе имеют право на существование. Однако может возникнуть ситуация, когда предпочтение должно быть отдано той или иной конкретной посылке. Например, если в последующем имеется необходимость перейти к нерекурсивному варианту программы, то лучше пользоваться посылкой первого типа, а если есть проблемы с доказательством правильности реализуемого алгоритма, то целесообразно работать с посылкой второго типа.

Нетрудно видеть, что общее количество рекурсивных вызовов при вычислении invest(sum,p,n) и invest1(sum,p,n) равно n. Можно было бы уменьшить это значение до величины floor(log2(n)) +1, где floor(a) - целая часть натурального числа a, исходя из следующих двух декомпозиционных посылок.

Пусть сумма sum=m× g денежных единиц помещена на вклад при ставке в p процентов за период. Тогда через n периодов sum возрастет до той же самой величины, что и совокупная сумма m отдельных вкладов по g денежных единиц каждый, также помещенных под р процентов за период. Не ограничивая общности, величину sum можно считать целым неотрицательным числом. В противном случае можно было бы перейти к иному номиналу денежных единиц. Значения m и g также будем считать целыми числами.

Положить некоторую сумму sum в банк на n периодов – это то же самое, что положить эту сумму на k (0£k£n) периодов, взять и снова положить на n-k периодов.

Основанную на этих посылках рекурсивную функцию для решения задачи 1 обозначим через inv(sum,p,n). Указанные посылки обнаруживают такие свойства этой функции.

Первая посылка.

В частности, при m=1 получаем:

Первая и вторая посылки. Пусть k=floor(n/2), тогда.

Отсюда при n=2×k сразу же получаем:

При n=2×k+1 имеем:

Выведенные соотношения для inv() позволяют записать такую программу для её вычисления:

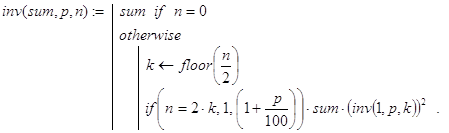
Общее количество рекурсивных вызовов при счете по этой программе-функции можно было бы подсчитать с помощью следующей вспомогательной рекурсивной функции:

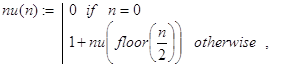
и оно действительно равно  

Контрольные примеры.

 

Незначительная перестройка структуры функции inv(sum,p,n) позволяет получить еще один вариант её реализации, в котором количество рекурсивных вызовов в точности равно  Сделать это можно так:

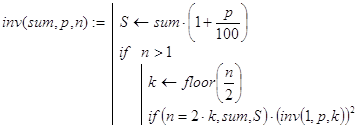
Замечание. В любых ситуациях, в которых возникают вопросы о быстродействии алгоритма, желательно по возможности минимизировать общее количество рекурсивных вызовов. В рассмотренной задаче построить алгоритм с рекурсивными вызовами можно было бы значительно проще, исходя из конечной формулы для решения задачи и дихотомии. Однако путь, который мы прошли, имеет свои достоинства. Он позволяет в общем случае выявить ограничения на рекурсивную функцию, достаточные для столь малого количества рекурсивных обращений при её вычислении. Фактически, из проведенных рассуждений вытекает такое утверждение.

Пусть функция F(a,n,v) удовлетворяет условиям:

F(a,1,v) =g(a,v),

F(a,n,v) =a×F(1,n,v),

F(a,n,v) =F(F(a,k,v),n-k,v) (1£k£n),

где a - действительное число, n - натуральное число, v=(v1,v2,…,vs) T - вектор с числовыми компонентами, g(a,v) - функция, значения которой для a и v из области определения F(a,n,v) мы вычислять можем. Тогда рекурсивная программа-функция:

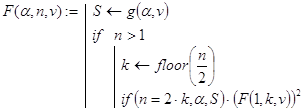
вычисляет значение F(a,n,v) ровно за рекурсивных вызовов.

Доказательство этого факта с использованием свойств A, B и C можно провести так:

 

Отсюда, при n=2×k имеем

а при n=2×k+1 получаем

Именно на этих соотношениях и базируется алгоритм, реализуемый программой-функцией F(a,n,v).

И в заключение замечания приведем пример функции, удовлетворяющей условиям A, B и С:  где в области определения функции f(v) её значения мы вычислят умеем.

Задача о величине вклада после снятия денег в конце каждого периода

Вкладчик положил в банк сумму в sum денежных единиц под p процентов за один период времени. В конце каждого периода вкладчик после начисления процентов снимает со счета A денежных единиц. Определить сумму вклада через n периодов времени.

Решение. Данная задача весьма похожа на задачу 1. Рекурсивная программа-функция waste(sum,p,A,n) реализует декомпозицию, исходя из такого утверждения. Положить сумму sum в банк на n периодов со снятием в конце каждого периода по A денежных единиц – это то же самое, что положить данную сумму на тех же условиях на n – 1 период, взять, снова положить на 1 период и затем снять A единиц.

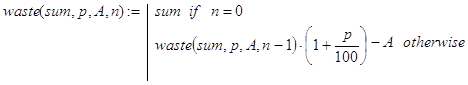 (3)

Нетрудно понять, на какую посылку опирается при декомпозиции рекурсивная программа-функция waste1(sum,p,A,n), решающая ту же самую задачу о динамике вклада.

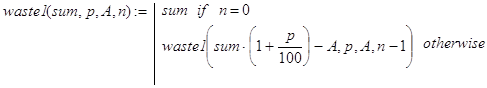 (4)

Замечание 1. Конечная формула для решения задачи 2 выглядит так:

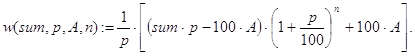
Выводится она следующим образом.

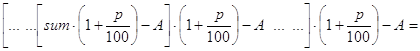
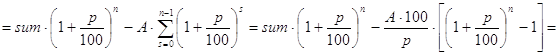
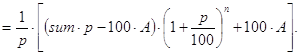
Одно из преимуществ “формул” waste() и waste1() в том, что они выписываются без всякого вывода и практически без затруднений.

Контрольные примеры.

 

Замечание 2. В связи с задачей о динамике вклада может быть поставлен и такой вопрос. Сколько лет подряд вкладчик может снимать со счета по A денежных единиц в конце каждого периода после начисления процентов, если он положил в банк сумму в S единиц при ставке p процентов. Ответ на него может дать рекурсивная функция year(S,p,A):

 

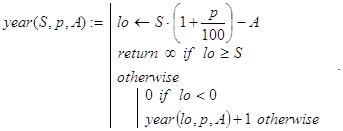
Здесь случай неубывания величины вклада выделен отдельно (lo³S), рекурсия организована по остаткам вклада после периодов, в которых хватило денег на очередную выплату в A единиц.

Контрольные примеры.

 

Задача о величине вклада после внесения (снятия) денег в конце или начале каждого периода

Вкладчик положил в банк pv денежных единиц на nper периодов при неизменной банковской ставке в rate процентов. В дальнейшем он предполагает в конце (type=0) или начале (type=1) каждого периода вносить (забирать) по pmt денежных единиц. Какой будет величина вклада через nper периодов?

Решение. Данная задача является прямым обобщением задач 1 и 2 и может быть решена с помощью встроенной в Excel функции fv(). Однако нас будут интересовать её рекурсивные аналоги. Будем считать, что знак величины pmt определяет тип операции, совершаемой вкладчиком в конце или начале каждого периода. При pmt³0 деньги вносятся на счет, а при pmt<0 деньги снимаются со счета (в Excel наоборот!). Далее, пусть знак pv определяет, имеет ли вкладчик деньги на счету или он должен банку. При pv³0 деньги на счету есть, при pv<0 имеется задолженность в |pv| денежных единиц (в Excel наоборот!).

Пусть fv(rate,nper,pmt,pv,type) - функция для решения исходной задачи. Ниже приведено два варианта (fv1(), fv2()) рекурсивной реализации fv():

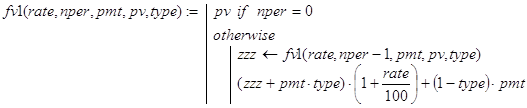
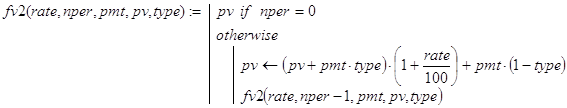
Дадим пояснения к функциям fv1() и fv2(), например, при type=0. Параметризация задачи фактически осуществлена в её постановке. Базой рекурсии для обоих предложенных вариантов служит случай nper=0. Иными словами, если pv денежных единиц положить в банк и сразу же их забрать, то будет возвращена та же самая сумма. Декомпозиция для fv1() и fv2() проведена, исходя из того, что решение исходной задачи по конечному результату равносильно соответственно совокупности следующих действий. Для fv1(): “Положить на тех же условиях pv денежных единиц в банк на nper-1 период, снять всю сумму с вклада и, наконец, на тех же условиях снова положить её на один период”. Для fv2(): “Положить на тех же условиях pv денежных единиц в банк на 1 период, снять всю сумму с вклада и, наконец, на тех же условиях снова положить её на nper-1 период”. Именно это и реализовано в соответствующих программах функциях.

При необходимости можно было бы вывести и конечную формулу для вычисления fv() или, по крайней мере, попытаться найти её в том или ином справочнике. Но это требует дополнительных усилий и затрат времени. Да и выглядит формула достаточно громоздко:

Задача о изменяющихся процентных ставках

В банк положена сумма в S денежных единиц. Пусть банк проводит начисления в процентах: в течение n0 периодов - по ставке p0, затем в течение n1 периодов - по ставке p1 и т.д. и, наконец, в течение nk-1 периодов - по ставке pk-1. Считая nj (j=0. . k-1) натуральными числами, вычислить размер вклада через n0+n1+…+nk-1 периодов.

Решение. Рассмотрим векторы длин периодов n и процентных ставок p:

n=(n0,n1,…,nk-1) T, p=(p0,p1,…,pk-1) T.

Данная задача является обобщением задачи 1 и при длине вектора n, равной единице, совпадает с ней. Пусть revise(S,p,n) - решение задачи 4. Тогда, в силу сказанного, при length(n) =1 имеем

revise(S,p,n) =invest(S,p,n),

и это соотношение может служить базой рекурсии. Декомпозицию реализуем, исходя из следующих соображений. Пусть length(n) >1 и задача 4 решена для векторов n1 и p1, полученных отбрасыванием последнего компонента соответственно у векторов n и p. Образовавшийся при этом новый размер вклада обозначим через sum. Тогда для получения решения исходной задачи с векторами n и p остается подсчитать сумму, возвращаемую при инвестировании величины sum на последние nk-1 периодов под pk-1 процентов. Иными словами, необходимо еще раз решить задачу 1, то есть вычислить значение функции invest(sum,pk-1,nk-1). Именно эти соображения и использованы при написании функции revise():

 

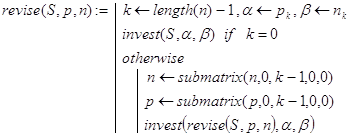
Рекурсивная функция revise1(S,p,n) построена на способе декомпозиции, вытекающем из таких соображений. Если исходную сумму S инвестировать под p0 процентов на n0 периодов, то с полученной суммой останется решить исходную задачу для векторов n и p c удаленными первыми компонентами:

 

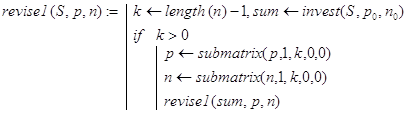
Замечание. При необходимости можно было бы вывести конечную формулу для решения задачи 4. Выглядит она так:

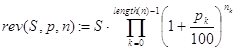
Контрольные примеры.

 

Задача о изменяющихся процентных ставках и величинах снимаемых денег

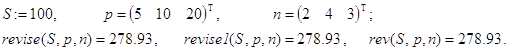
Вкладчик положил в сбербанк sum денежных единиц под pk (k=0. . n-1) процентов за каждый из n последующих периодов времени. В конце каждого периода k (k=0. . n-1) после начисления pk процентов он снимает со счета Ak денежных единиц. Иными словами, допускается, вообще говоря, и изменение процентной ставки, и величины денежных единиц, снимаемых с вклада. Составить программы, отвечающие на следующие вопросы:

Имеет ли задача решение?

Если задача имеет решение, то какова величина вклада после n периодов?

Если задача не имеет решения, то каков наименьший номер периода, в котором взятие соответствующей суммы оказалось невозможным?

Решение. Рассмотрим векторы процентных ставок и величин уменьшения вклада:

p=(p0,p1,…,pn-1) T, A=(A0,A1,…,An-1) T.

Ответ на первые два вопроса дают рекурсивные программы-функции waste2(sum,p,A) и waste3(sum,p,A). Если задача имеет решение, то они возвращают величину вклада после n периодов, а иначе - отрицательное число. Декомпозиция для функции waste2() проводилась, исходя из того же утверждения, что и для функции waste(), а декомпозиция для функции waste3() - исходя из того же утверждения, что и для функции waste1(). Во втором случае получена более компактная и ясная программа:

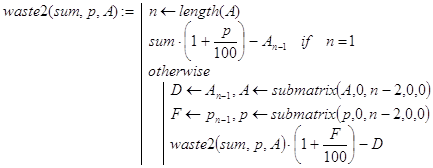
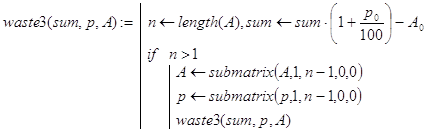
Наряду с этими программами можно вывести и конечную формулу wa(S,p,A) для расчетов. Пусть n=length(p). Тогда:

 

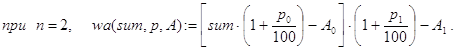
И, наконец, в общем случае:

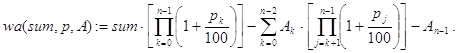
Контрольные примеры.

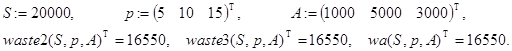
Попробуем теперь составить программу, отвечающую на третий из поставленных вопросов. Будем считать, что она должна возвращать вектор с двумя компонентами, который выглядит так:

[“O’key” решение] T, если задача имеет решение;

[период сальдо] T, если задача не имеет решения.

Во втором случае возвращается период (нумерация от 1 и далее) и отрицательное сальдо – количество денежных единиц, которых недостает для выплаты в данный период.

Всем перечисленным условиям удовлетворяет рекурсивная программа-функция waste4(sum,p,A,k):

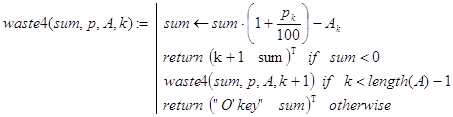
Здесь k - вспомогательный параметр. При первом обращении к waste4() его значение должно быть равно нулю. Далее k используется для организации рекурсивных вычислений, а операторы return - для прекращения рекурсивных вызовов при получении решения задачи.

Контрольные примеры.

 

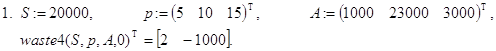
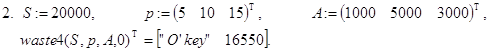
Дисконтирование. Инвестиции. Консолидирование Задача о дисконтировании

Какую сумму следует внести сегодня в банк при процентной ставке p, чтобы через n периодов получить S денежных единиц?

Решение. Фактически речь идет о вычислении величины, называемой экономистами современной стоимостью отложенного платежа. Если положить в банк сумму в R=S/(1+p/100) n единиц, то через n периодов она превращается в S единиц. Та же самая сумма R через n-1 период превращается в S/(1+p/100) единиц. Таким образом, если discount(S,p,n) - решение исходной задачи, то при n¹0 имеем:

discount(S,p,n) = discount(S/(1+p/100),p,n-1).

Будем проводить рекурсию по количеству периодов n. Тогда последнее соотношение дает нам правило декомпозиции. Отсюда и получаем программу-функцию 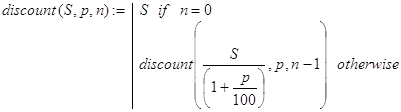(5):

 (5)

На вопросе о том, как проведена декомпозиция в (6), останавливаться не будем:

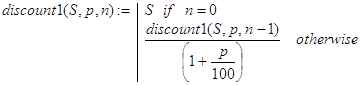 (6)

Замечание. Из проведенных рассуждений вытекает, что решение задачи может быть получено по конечной формуле:

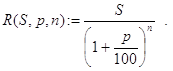
Контрольные примеры.

Задача о современной стоимости потока равных платежей.

Пусть реализация некоторого проекта обеспечивает поток равных платежей по S денежных единиц за каждый из n периодов при банковской ставке p процентов. Подсчитать современную стоимость этого потока.

Решение. Если просуммировать сегодняшнюю стоимость первого, второго и т.д. и, наконец, последнего платежа, то мы и получим современную стоимость всего потока. Пусть она равна payment(S,p,n). Тогда в силу задачи 6 о дисконтировании будем иметь:

Впрочем, никто не мешает нам вывести и конечную формулу для расчетов, которая выглядит так:

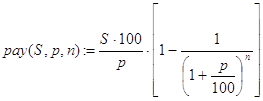
Однако мы займемся написанием рекурсивной программы-функции решения данной задачи. Выделить базу и провести декомпозицию наиболее просто, исходя из таких утверждений. Если n=0, то есть не прошло ни одного периода, то и платежей поступит 0. Далее, современная стоимость всех платежей - это современная стоимость платежей за первые n-1 период плюс современная стоимость последнего n-го платежа, равного S/(1+p/100) n. Отсюда и получаем функцию 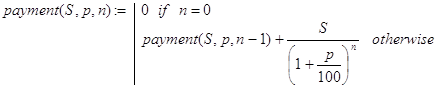(7):

 (7)

Другой вариант рекурсивной функции решения задачи 7 можно записать так:

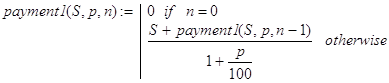 (8)

Контрольные примеры.

 

Задача о инвестировании проекта

Пусть некоторый проект в течение последующих nper периодов будет приносить доход по pmt денежных единиц. Пусть платежи инвестору производятся в конце каждого периода (type=0) или в начале их (type=1). Какую сумму инвестор может вложить в этот проект, чтобы при действующей процентной ставке, равной rate за период, он оказался выгодным?

Решение. Вопрос фактически ставится так. Если сегодня инвестор внес W денежных единиц в реализацию проекта, то оправданы ли эти затраты с его будущими доходами по pmt единиц в течение каждого из nper периодов? Из предыдущей задачи вытекает, что при type=0 проект оказывается выгодным лишь при выполнении условия W<payment(pmt,nper,rate). В общем виде эта задача является прямым обобщением задачи 7 и может быть решена с помощью встроенной в Excel функции pv() - вычисления современной стоимости потока равных платежей. Если W<pv(pmt,nper,rate,type), то финансировать проект выгодно. Сконструируем рекурсивныe аналоги pv1() и pv2() функции pv(). Рассмотрим два варианта.

Вариант 1. Функции pv10() и pv11() вычисляют современную стоимость потока платежей соответственно при type=0 и type=1. При этом pv10() равносильна функции (7), а pv11() строится по аналогии с pv10(). Далее, при известных функциях pv1() и pv2() написание функции pv1() для любого значения type труда не представляет:

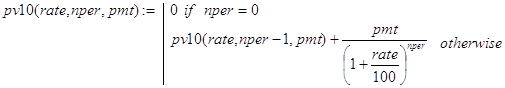
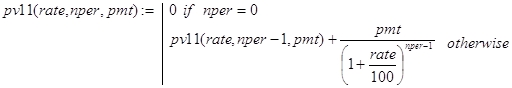
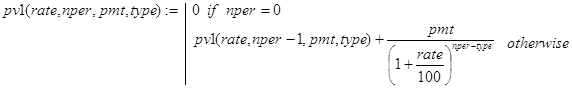
Вариант 2. Функции pv20() и pv21() вычисляют современную стоимость потока платежей соответственно при type=0 и type=1. При этом pv20() равносильна функции (8), а pv2() строится по аналогии с pv20(). Далее, при известных функциях pv20() и pv21() написание функции pv2() для любого значения type труда не представляет:

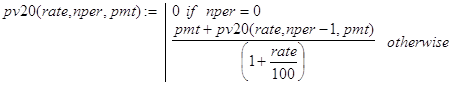
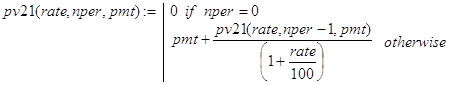
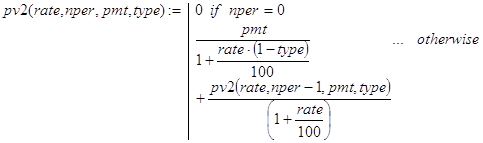
Вывод конечной формулы для расчета pv() можно провести так.

type=0.

type=1.

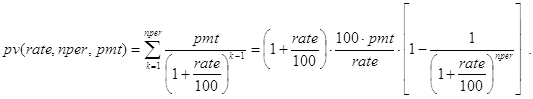
Общий случай.

Контрольные примеры.

Задача о консолидировании платежей

Заемщик при существующей ставке в p процентов должен внести в банк k последовательных платежей. Первый платеж в a0 денежных единиц необходимо осуществить через t0 периодов, второй платеж в a1 единиц - через t1 периодов и т.д. и, наконец, k-й платеж в ak-1 единиц - через tk-1 периодов. Все величины tn (n=0. . k-1) отсчитываются от момента получения займа. Из-за невозможности внести первый взнос заемщик просит консолидировать его платежи, то есть разрешить ему через некоторое время заплатить сразу весь долг a0+a1+…+ak-1. Через какое количество q периодов заемщик обязан рассчитаться, чтобы ничьи интересы не пострадали?

Решение. Будем исходить из того, что современная стоимость потока платежей заемщика и современная стоимость единовременно вносимой им суммы должны совпадать. Отсюда для нахождения значения q получаем так называемое уравнение эквивалентности процентных ставок при дисконтировании:

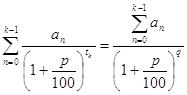 (9)

Параметр q можно непосредственно определить из этой формулы. Пусть a и t - векторы платежей и периодов:

a=(a0,a1,…,ak-1) T, t=(t0,t1,…,tk-1) T. (10)

Будем вычислять q с помощью функции conso(a,t,p) и вспомогательной рекурсивной функции summa(a,t,p), служащей для нахождения сумм в (9). Значение q=conso(a,t,p) может оказаться дробным.

Выглядят эти функции так:

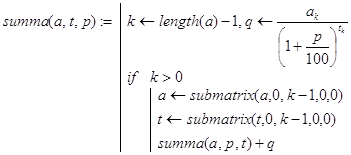 (11)

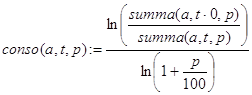 (12)

Замечание. Величины tn (n=0. . k-1) можно измерять в долях целого периода. Например, если один период - это год, то tn можно измерять в месяцах, днях, а при необходимости - и в часах. При этом процентная ставка p должна быть скорректирована соответственно на p/12, p/365 или p/(365×24).

Контрольные примеры.

 

Платежи Задача о равных платежах в конце каждого периода

Банк выдал заемщику кредит в S денежных единиц на k периодов с необходимостью выплаты долга равными частями в конце каждого периода. Определить величину разовых выплат, если процентная ставка банка за один период равна p.

Решение. Эта задача весьма поучительна. Она дает нам возможность на конкретном примере поговорить об одном необычном способе построения эффективных рекурсивных алгоритмов решения определенного класса задач, отправляясь от “алгоритмов с бесконечным числом рекурсивных обращений”. Обозначим через pay(S,p,k) решение задачи. Попробуем обсудить приведенный ниже текст программы вычисления pay(S,p,k):

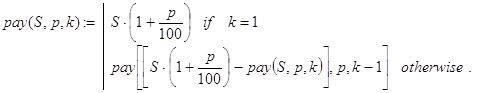 (13)

С точки зрения логики здесь как будто бы все в порядке. Фактически записано, что если k=1, то есть расчет должен произойти в конце первого периода, то выплатить придется всю задолженность сразу, а именно, S×(1+p/100) денежных единиц. В противном случае необходимо поступить так. Произвести расчет в конце первого периода и с оставшейся задолженностью

 (14)

рассчитываться следующие k-1 периодов. Что же в этом рассуждении не работает? Дело в том, что в (14) величина pay(S,p,k) неизвестна. Именно её по условию задачи и требуется вычислить. Поэтому попытка реально реализовать счет по программе-функции (13) всегда будет завершаться аварийно - переполнением стека рекурсивных вызовов. Иными словами, тело рекурсивной функции не может содержать ссылку на эту же функцию с тем же самым набором параметров! Но не будем отчаиваться. Подставим в теле (13) вместо pay(S,p,k) некоторый параметр X:

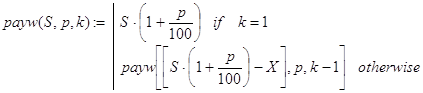 (15)

Полученная функция payw() при любом фиксированном X уже вполне пригодна для вычислений. Здесь рекурсия четко организована по параметру k. Правда, непонятно, что payw() вычисляет? Но это и знать незачем. Все, что нам требуется - это зафиксировать X не произвольно, а таким образом, чтобы полученное в результате вычислений по (15) значение для payw(S,p,k) оказалось равным X. В этом случае фактически будет вычислено pay(S,p,k) в (13), то есть решена исходная задача. Однако метод хаотичных проб и ошибок вряд ли здесь может привести к успеху. Необходимо научиться управлять параметром X, изменяя его значение в правильном направлении. Для этих целей к аргументам функции payw(S,p,k) добавим X:

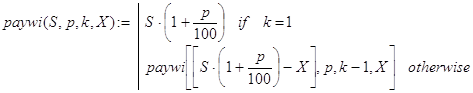 (16)

Получили функцию paywi(). При любом фиксированном X значения функций (15) и (16) равны. Поэтому поиск решения исходной задачи окончательно свелся к нахождению в (16) такого X, при котором

g(S,p,k,X) ºpaywi(S,p,k,X) - X=0.

Фиксируем значения S, p и k. Тогда g(S,p,k,X) - непрерывная на всей числовой оси функция одной переменной. Нам необходимо найти по крайней мере один её вещественный корень X* (g(S,p,k,X*) º0). Делать это можно по-разному. Например, определить отрезок, на котором g() принимает значения разных знаков, а затем использовать быстро сходящийся метод дихотомии (деления отрезка пополам).

Приведенная ниже рекурсивная программа-функция dicho(f,a,b,e) для произвольной непрерывной на отрезке [a,b] (a<b) функции f(x) при условии f(a) ×f(b) £0 c заданной точностью e>0 находит некоторый вещественный корень f(x). Эту функцию и будем использовать далее:

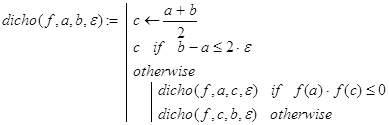 (17)

Контрольный пример. Подсчитать величину равных платежей в конце каждого периода, если заем в 1000 денежных единиц взят под 10 процентов на каждый из 4 периодов.

 

Предложенный способ решения задачи (10) не является наилучшим. Можно было бы для этих целей предложить и такие рекурсивные функции:

 (18)

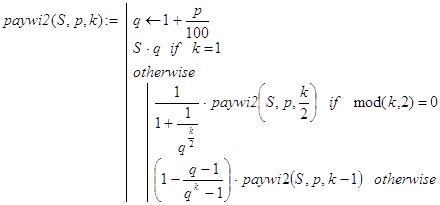 (19)

Функция paywi1() отличается от функции paywi2() количеством рекурсивных вызовов при вычислениях. Порядок их в первом случае равен k, а во втором - log2(k).

Решение предложенной задачи может быть осуществлено и по конечной формуле (20). Выводится она так. Пусть W=W(S,p,k). С одной стороны, задолженность через k периодов должна быть полностью погашена, а с другой - её можно подсчитать так:

Приравнивая последнее выражение нулю, и разрешая полученное уравнение относительно W, получаем формулу (20):

 (20)

Контрольные примеры.

 

Замечание. Мы решали задачу, предполагая, что платежи поступают в конце каждого из периодов. Это совсем не обязательно. Формула (20) остается справедливой (с поправками) и в следующих двух случаях:

Производится по m1 платежей через равные промежутки времени в каждый из k периодов. В (20) вместо k и p необходимо подставить соответственно значения k×m1 и p/m1.

Платежи проводятся через m2 периодов. В (20) вместо k и p необходимо подставить соответственно значения k/m2 и p×m2.

Указанное замечание касается и многих других ранее рассмотренных функций.

Задача о равных платежах в конце или начале каждого периода.

Банк выдал заемщику кредит в pv денежных единиц на nper периодов с необходимостью выплаты долга равными частями в конце (type=0) или начале (type=1) каждого периода. Определить величину pmt разовых выплат, если процентная ставка банка за один период равна rate.

Решение. Данная задача может быть решена с помощью встроенной в Excel функции pmt=pmt(rate,nper,pv,type). При type=0 задачи 10 и 11 идентичны. Ниже приведено решение для общего случая, основанное на легко получаемой рекуррентной формуле. Будем исходить из того, что современная стоимость всех внесенных платежей должна быть равной произведенному займу pv. Пусть через pmtn (n=1,2,…) обозначена ставка платежей при выплатах за n периодов. Найдем связь между pmtn и pmtn-1, исходя из баланса современной стоимости платежей при любом n. Пусть type=0. Тогда

 

Отсюда

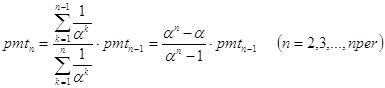 (21)

То же самое соотношение получается и для type=1. Иными словами, при любом допустимом значении type имеет место следующая рекуррентная формула:

 (22)

Раскрывая рекуррентность (22), получаем

 (23)

 (24)

Соотношения (24) и (22) и взяты соответственно в качестве базы и декомпозиции при реализации рекурсивной программы-функции pmt():

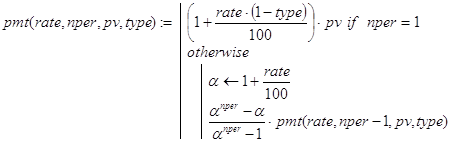
Из соотношений (23) и (24) при n=nper получается конечная формула для вычисления значений pmt():

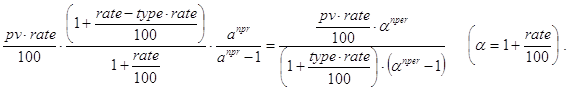
Контрольные примеры.

 

Задача о платежах с одинаковой современной стоимостью

Некто занял pv денежных единиц на nper периодов при процентной ставке в rate процентов за период. Платежи ppmt по займу должны иметь одинаковую современную стоимость и производиться в конце (type=0) или начале (type=1) каждого периода. Определить величину платежа в период per (per=1,2,…,nper).

Решение. Данная задача может быть решена с помощью встроенной в Excel функции ppmt(rate,per,nper,pv,type). Получим её рекурсивную реализацию. Пусть pk (k=1,2,…,nper) - последовательные платежи.

Рассмотрим сначала случай type=0. Современные стоимости всех платежей должны совпадать. Отсюда

 (25)

Но

 (26)

Аналогично при type=1 получим

 (27)

Из соотношений (25), (26) и (27) нетрудно получить соответствующие формулы для случая произвольного значения type. Выглядят они так:

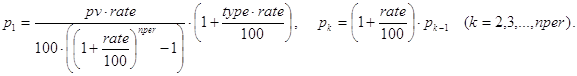
Теперь ясно, что брать в качестве базы рекурсии, и как организовать декомпозицию по периодам при построении функции ppmt(), а также как получить конечную формулу (ppmt1) для решения исходной задачи:

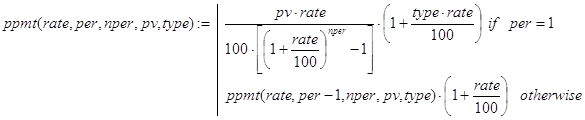
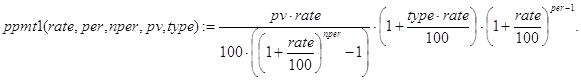
Контрольные примеры.

Задача о платежах на проценты

Некто взял заем в pv денежных единиц при ставке rate процентов за период. Возврат долга должен быть произведен nper равными платежами в конце каждого периода. Подсчитать платеж ipmt в период per (1£per£nper), составляющий часть общего платежа, равную приросту долга по процентам за этот период.

Решение. Данная задача может быть решена с помощью встроенной в Excel функции ipmt(rate,per,nper,pv). Получим её рекурсивную реализацию. Общая величина платежа pmt в каждый из периодов может быть вычислена так (см. задачу 11 при type=0):

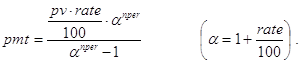
Базой рекурсии будем считать случай per=1. К концу первого периода часть долга, приходящаяся на проценты, будет равна pv×rate/100. Декомпозицию проведем, опираясь на такие соображения. Решать исходную задачу, вычисляя ipmt в период per - это то же самое, что решать укороченную на один период задачу, но с начальным займом в pv×(1+rate/100) -pmt денежных единиц. Тогда решение задачи можно получать с помощью пары функций ipmt() и ip(). Первая из них вычисляет вспомогательную величину pmt - размер общих платежей в конце каждого периода, и передает её в качестве формального параметра функции ip(), в которой и организуется описанный рекурсивный процесс:

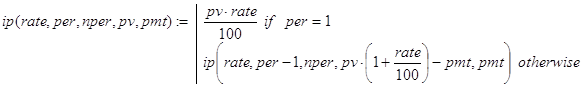
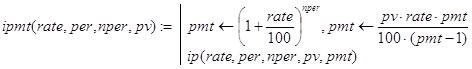
Вывести конечную формулу (ipmt1) для решения задачи можно так. Остаток долга после завершения (k-1) - го периода равен:

Тогда увеличение долга по процентам за k-ый период можно подсчитать так:

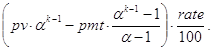
Но это и есть прирост долга по процентам за k-ый период. И окончательно имеем:

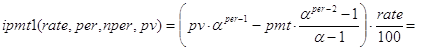
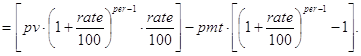
Контрольные примеры.

Разные задачи Задача о величине процентной ставки

Банк выдал заемщику S денежных единиц. Условия кредита таковы: заемщик должен внести в банк k последовательных платежей. Первый платеж в a0 денежных единиц необходимо осуществить через t0 периодов, второй платеж в a1 единиц - через t1 периодов и т.д. и, наконец, (k-1) - й платеж в ak-1 единиц - через tk-1 периодов. Все величины tn (n=0. . k-1) отсчитываются от момента получения займа. Какую процентную ставку установил банк для этого кредита?

Решение. Пусть p - процентная ставка и x=1+p/100. Считая, что современная стоимость всех внесенных в банк платежей должна равняться величине кредита, получаем:

 

Но t0<t1<…<tk-1 и для нахождения величины x, а значит и p, имеем уравнение:

Нам требуется определить положительный корень многочлена f(x), стоящего в левой части последнего соотношения. Из экономических соображений вытекает, что такой корень должен существовать и быть единственным. Впрочем, с учетом того, что S>0 и an>0 (n=0. . k-1), чисто формальными рассуждениями можно установить даже более сильное утверждение. Многочлен f(x) имеет единственный неотрицательный корень x0. Модули остальных его корней не превосходят x0. Доказательство этого факта вытекает из применения теоремы Фробениуса-Перона [8, c.263; 9, стр.319, 340] к сопровождающей матрице f(x).

Схема дальнейшей нашей работы будет такой. Пусть векторы a и t - заданы соотношениями (10). Напишем рекурсивную программу-функцию vecto() формирования компонентов вектора m коэффициентами f(x), начиная от свободного члена a0 и далее по возрастающим степеням x. Затем в головной программе percent(S,a,t) для нахождения процентной ставки p воспользуемся композицией серии встроенных в Mathcad функций:

polyroots(m) – вычисление всех корней f(x);

max(v) - нахождение числа a+i×b, где a и b наибольшие соответственно из действительных частей и коэффициентов при мнимых частях компонентов v;

Re(z) - вычисление действительной части комплексного числа z.

 (28)

 (29)

Несколько слов об аргументах функции vecto(a,t,n,q,m). Назначение величин a, t и n ясно. Вспомогательный параметр q служит счетчиком количества сформированных в матрице m коэффициентов f(x): q=0. . tn.

Нерекурсивный вариант программ (28) -(29) может быть записан так:

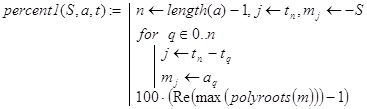 (30)

Контрольные примеры.

 

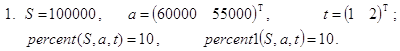
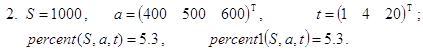
Задача о величине процентной ставки 2

Инвестор вложил в некоторый проект pv денежных единиц (д. е) и в течение последующих nper периодов это должно приносить ему платежи по pmt д. е. Пусть платежи производятся в конце (type=1) или в начале (type=0) каждого периода. Под какой процент вложены инвестором деньги?

Решение. Данная задача может быть решена с помощью встроенной в Excel функции rate(nper,per,pv,type). Строя рекурсивные аналоги rate(), будем делать это отдельно для случаев type=0 и type=1.

A. type=0. Современная стоимость всех платежей должна быть равна pv:

 (31)

Преобразуем (31) к виду

 (32)

На последнее соотношение можно смотреть как на декомпозицию исходной задачи с прежними платежами и процентной ставкой, nper-1 периодом и инвестициями в pv×(1+rate/100) -pmt денежных единиц. Правда, инвестиции здесь содержат неизвестный параметр rate. Далее ясно, что при nper=1

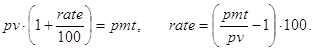
Если считать последнее из этих соотношений базой индукции, то соответствующая программа-функция могла бы выглядеть так:

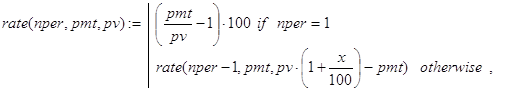 (33)

где за x обозначена величина rate(nper,pmt,pv). Мы получили, что в процессе рекурсивных вызовов функция обращается к самой себе с тем же самым набором значений параметров. Ясно, что вычисления по ней не будут иметь останова. Точнее, останов будет аварийным по переполнению стека. С подобной ситуацией мы уже сталкивались при решении задачи 10. И там для выхода из создавшейся ситуации был использован прием введения дополнительного параметра. Поступим также и здесь, заменив (33) функцией:

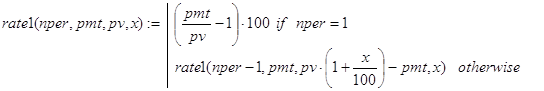 (34)

Теперь будем искать решения x=x* уравнения

 (35)

Делать это можно, например, методом дихотомии с помощью рекурсивной функции dicho() (см. (17)).

Замечание. Обратим внимание на следующее обстоятельство. При решении уравнения g(nper,pmt,pv,x) =0 с вычислениями по (34) могут появиться “посторонние корни” - значения x* º rate1(nper,pmt,pv,x*), но не являющиеся решениями исходной задачи. Поэтому все полученные корни (35) обязаны подвергнуться проверке по данным задачи, например, на выполнимость условия (31). Ограничимся рассмотрением одного примера.

Контрольный пример.

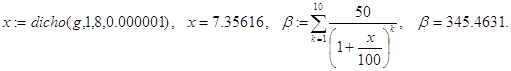
Полученное значение x=7.35616 не является решением задачи, ибо pv=320.88289¹b.

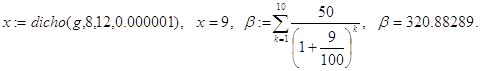
Получили решение задачи, ибо pv=320.88289=b.

B. type=1. К началу второго периода задолженность инвестору с одной стороны равна (pv-pmt) ×(1+rate/100), а с другой стороны - должна быть погашена вторым платежом pmt. Таким образом

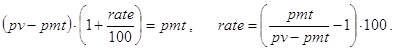 (36)

Далее,

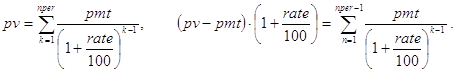 (37)

Последние соотношения в (36) и (37) задают соответственно базу и декомпозицию, на основе которых после введения дополнительного параметра x и построена рекурсивная функция rate2():

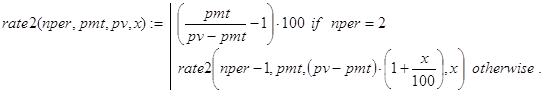
Все дальнейшие действия должны быть такими же, как и в случае type=0.

Задача о количестве периодов для расчета заемщика с банком

Клиент банка получил заем в S денежных единиц при ставке p процентов. В конце каждого периода заемщик должен возвращать банку по W единиц, за исключением может быть последнего периода, когда его задолженность Z окажется меньшей W. В этом случае необходимо возвратить Z единиц. Подсчитать количество периодов, необходимых для расчета заемщика с банком.

Решение. Организуем рекурсию по величине долга в конце каждого периода. Если R=S×(1+p/100) -W£0, то полностью расплатиться удастся за один период, и условие R£0 можно взять в качестве базы рекурсии. Нетрудно понять, что при R=S долг всегда будет одним и тем же, а при R>S он будет возрастать. Таким образом, при R³S рассчитаться с долгом вообще не удастся. Пусть R<S. Декомпозицию проведем, исходя из такого утверждения. Если с долгом величиной S можно рассчитаться за k периодов, то с долгом величиной R удастся рассчитаться за k-1 период. Эти соображения и легли в основу формирования функции number(S,p,W):

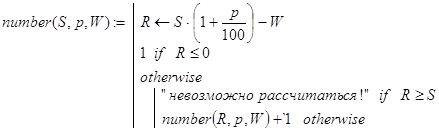 (38)

Разберем еще один вариант решения данной задачи. Пусть a=1+p/100. Тогда:

 - долг через 1 период;

 - долг через 2 периода;

… … …

 - долг через k периодов;

Отсюда, прежде всего, вытекает, что с долгом удастся расплатиться, если S×p/100<W, то есть его увеличение за первый период должно быть меньше разового платежа. Впрочем, это было ясно и из предыдущих рассуждений. Далее, последнее соотношение говорит о том, что при S×p/100<W долг будет погашен через k периодов, где k - наименьшее натуральное число, удовлетворяющее неравенству:

Рассмотрим рекурсивную функцию number1(S,p,W,k):

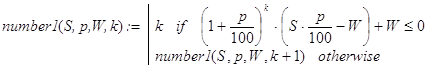 (39)

с некоторым вспомогательным натуральным аргументом k. Ясно, что при обращении к ней с любыми значениями S, p и W (S×p/100<W) и k=1 получим решение исходной задачи. Обратите внимание на отсутствие отложенных вычислений при реализации number1(S,p,W,k).

Контрольные примеры.

Замечание. Из предыдущих рассуждений вытекает, что решение задачи 16 можно получать так. Вычислить значение функции

(логарифм десятичный) и взять наименьшее целое, большее или равное num(S,p,W).

Рассмотрим еще одну задачу, проливающую свет на то, как банки “делают деньги”. Пусть имеется система из n банков B1, B2,..., Bn, для каждого из которых установлена норма резервов в p процентов. Это означает, что любой из этих банков p процентов своих наличных денег должен хранить в некотором Центральном банке B0 в виде обязательных резервов. Остальные деньги являются свободными резервами банков. Их можно давать в кредит под определенные проценты, вкладывать в различные проекты, а из полученных доходов выплачивать вкладчикам проценты за пользование их деньгами.

Задача о суммарной способности к кредитованию

Пусть в банк B1 внесен вклад в S денежных единиц. Будем считать, что свободные резервы банка Bk (k=1,2,...,n-1) в результате ряда операций становятся вкладом в банк Bk+1 (k=1,2,...,n-1), а норма обязательных резервов равна p процентов. Определить суммарную способность к кредитованию рассматриваемой системы банков.

Решение. Получить решение данной задачи можно по рекурсивной функции credit(S,p,n). Декомпозиция в ней реализована, исходя из следующей посылки. Суммарная величина кредитования всей системы банков складывается из величины кредитования банка B1 и суммы величин кредитования остальных банков с учетом того, что вклад в банк B2 составил S×(1-p/100) денежных единиц. База рекурсии также очевидна: нет банков (n=0) - нет кредитования.

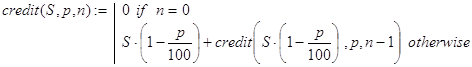
Вывод конечной формулы для решения задачи (10) может быть проведен так:

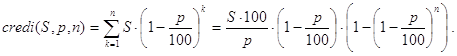 (40)

Контрольные примеры.

 

Какие же выводы можно сделать из рассмотрения последней задачи? В системе коммерческих банков B1, B2,..., Bn не предполагалось, что все они различны. Более того, допустим и такой крайний случай: B1 = B2 =... = Bn. Поэтому способность системы банков к кредитованию, вообще говоря, не связана с их количеством. Но эта способность существенно связана с оперативным возвратом отдаваемых в кредит денег, после серии сделок с ними, снова в банки в виде вкладов. Кроме того ясно, как центральный банк путем изменения ставки обязательных резервов может влиять на суммарный объем кредитования. Если процент обязательных резервов растет, то суммарная величина кредитов убывает, если же этот процент уменьшается, то суммарная величина кредитов возрастает.

Задача о минимальном количестве банков

Пусть в банк B1 внесен вклад в S денежных единиц. Будем считать, что свободные резервы банка Bk (k=1,2,...,n-1) в результате ряда операций становятся вкладом в банк Bk+1 (k=1,2,...,n-1), а норма обязательных резервов равна p процентов. Определить минимальное количество n системы банков Bk (k=1,2,...,n), для которых суммарная способность к кредитованию не меньше заданной величины H.

Решение. Здесь, как и в предыдущей задаче, не предполагается, что все банки Bk (k=1,2,...,n) различны. Поэтому фактически речь идет не о минимальном количестве банков, обеспечивающих кредитование, не меньшее заданной величины H, а о минимальном количестве (оперативных) возвратов в банки денег, отдаваемых в кредит. Но нам удобней вести речь о количестве банков. Прежде всего, из общей формулы (40) вытекает, что данная задача не всегда имеет решение. При бесконечной системе банков предельная сумма кредитования равна L(S,p) = (S×100/p) ×(1-p/100). Поэтому решать задачу можно лишь при условии H<L(S,p). Найти n можно, как наименьшее натуральное решение неравенства

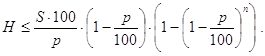
Мы будем вычислять n с помощью функций findn() и num():

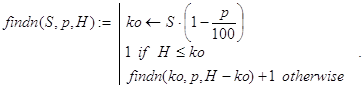
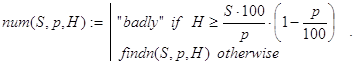
Декомпозиция в рекурсии для findn(S,p,H) организована по величинам оставшегося неудовлетворенным кредита по мере увеличения числа банков в системе.

Контрольные примеры.

Задача о изменении величины суммарного кредитования

Пусть в банк B1 внесен вклад в S денежных единиц. Будем считать, что свободные резервы банка Bk (k=1,2,...,n-1) в результате ряда операций становятся вкладом в банк Bk+1 (k=1,2,...,n-1), а норма обязательных резервов установлена в p (0<p<100) процентов. Изменить ставку p так, чтобы суммарная величина кредитов, предоставляемых всеми банками, изменилась в a>0 (a¹1) раз, то есть либо увеличилась в a раз при a>1, либо уменьшилась в 1/a раз при 0<a<1.

Решение. Сразу отметим, что как и в предыдущей задаче не предполагается, что все банки Bk (k=1,2,...,n) различны. Задача, по-видимому, не всегда имеет решение. Если решение x есть, то как его искать? На помощь может прийти формула (40). В соответствии с ней имеем:

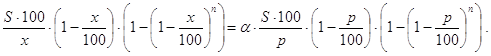
Сократим обе части этого соотношения на S×100 и, обозначив правую часть через b:

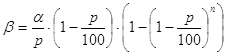
для нахождения решений задачи получим уравнение:

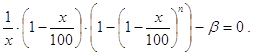 (41)

Последовательно преобразуем правую часть (41):

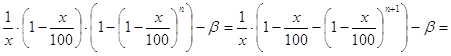
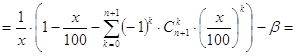
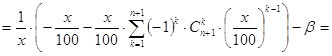
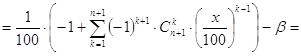
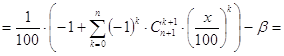
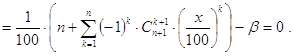
Следовательно, если x есть решение задачи, то его следует искать среди действительных корней многочлена g(t) (t=x/100) степени n, где

 (42)

со следующим вектором коэффициентов:

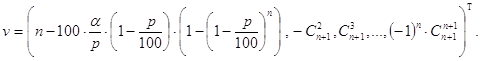 (43)

При этом, по смыслу задачи у многочлена (42) на промежутке (0,1) может быть не более одного корня t=x/100.

Таким образом, решение исходной задачи свелось к нахождению для многочлена g(t) c коэффициентами (43) действительного корня t: 0<t<1. Если такой корень отсутствует, то исходная задача решений не имеет, то есть, только за счет изменения текущей процентной ставки обязательных резервов изменить суммарную величину кредитов системы коммерческих банков в a раз не удастся. Если же корень tÎ(0,1) найден, то решением задачи является величина x=t×100. Иными словами, если назначить процентную ставку обязательных резервов в t×100 процентов, то суммарная величина кредитов измениться в a раз.

Решение исходной задачи может быть найдено с помощью функции times(n,p,a), обращающейся к следующим рекурсивным функциям: pow(a,n), C(n,m), binom2(n,k) и finroo(v). Ниже приведено краткое описание всех этих функций.

pow(a,n) - быстрое возведение действительного или комплексного числа a в целую неотрицательную степень n. Декомпозиция в рекурсии организована с помощью дихотомии - последовательными уменьшениями степени в два раза, то есть представлением a в виде:

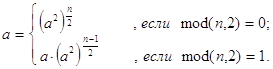
C(n,m) - вычисление количества сочетаний из n элементов по m элементов. Декомпозиция в рекурсии организована в соответствии с известной формулой:

binom2(n,k) - вычисление последовательности биномиальных коэффициентов  со знаком  Декомпозиция в рекурсии организована по величине аргумента s. База рекурсии соответствует значению s=2.

finroo(v) - нахождение в векторе v первой из компонент t, удовлетворяющей условию (Im(t) =0) ×(Re(t) Î(0,1)). Если таковых компонент не имеется, то возвращается значение, равное ¥. Декомпозиция в рекурсии организована по значению длины меняющегося вектора v.

times(n,p,a) - с помощью функций pow(), С() и binom2() находится вектор v коэффициентов (43) многочлена (42). После этого с использованием встроенной функции polyroots(v) отыскиваются корни многочлена (42). При написании программы-функции times(n,p,a) учтено утверждение критерия существования решения задачи, сформулированное ниже в виде леммы 1:

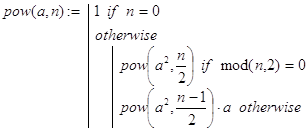
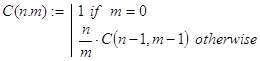
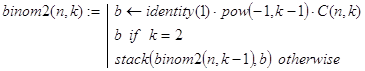
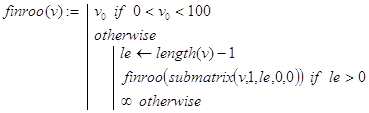
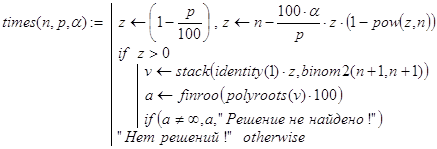
Замечание. Поскольку встроенная функция polyroots() находит значения корней приближенно, то даже при точных коэффициентах многочлена g(t) вместо корня tÎ(0,1) мы можем получить близкий к нему комплексный корень t1 с Re(t1) Î(0,1) и Im(t1) ¹0. Тогда функция times() сообщит об отсутствии решения исходной задачи. Но это может быть и не так. Поэтому получение такого сообщения требует более тщательного анализа корней многочлена (42). Например, искать требуемый вещественный корень в промежутке (0,1) с заданной степенью точности можно методом дихотомии. При этом следует исходить из следующего утверждения.

Лемма 1. Для существования решения исходной задачи необходима и достаточна положительность свободного члена многочлена (42), то есть выполнение условия g(0) >0. Иначе это условие можно записать в виде n>100×b или, по-другому,

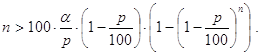
Доказательство. Необходимость. Пусть решение x исходной задачи существует. Тогда, как мы уже отмечали, его следует искать среди действительных корней многочлена g(t) (t=x/100 Î (0,1)). Нам понадобится значение g(t) в нуле: g(0) =n-100×b. Пусть t*Î(0,1) - корень g(t). В этом случае

 (44)

Но при любом t*Î(0,1) справедливо неравенство:

 (45)

Последний переход в (45) сделан с использованием одного замечательного неравенства [13, c.24-27]:

xq - q×x + q -1 > 0 (x > 0, q > 1),

легко устанавливаемого с помощью методов дифференциального исчисления и являющегося основой для доказательства многих классических неравенств таких, например, как основные неравенства Гельдера и Минковского. Но тогда из (44) следует, что g(0) >0 и необходимость установлена.

Достаточность. Пусть выполнено условие g(0) >0. Подсчитаем значение функции g(t) в точке 1:

Последнее неравенство вместе с предположением g(0) >0 гарантирует наличие у многочлена g(t) действительного корня t*Î(0,1), а значит и решения x=t*×100 исходной задачи. Тем самым установлена достаточность, и лемма полностью доказана.

Дополнение 1 к задаче 19. Пусть банки Bk (k=1,2,...,n) функционируют так, как это описано в условиях задачи 19. Можно ли на r процентов (-100<r) изменить суммарную величину кредитов, предоставляемую банками? Если это возможно, то найти новую ставку обязательных резервов.

Решение. Заметим, что если r>0, то величина кредитов увеличивается, а если r<0, то она уменьшается. Далее, поскольку изменение суммарной величины кредитов на r процентов равносильно их изменению в 1+r/100 раз, то необходимо просто решать задачу 19 c a=(1+r/100). Условие существования решения (см. лемму 1) в данном случае запишется так:

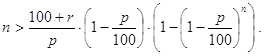
Дополнение 2 к задаче 19. Пусть банки Bk (k=1,2,...,n) функционируют так, как это описано в условиях задачи 19. Определить начальную процентную ставку p обязательных резервов, если её изменение до p1 процентов привело к изменению суммарной величины кредитов в b раз.

Решение. Согласно (40)

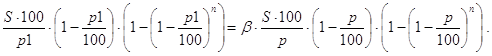
Если считать p неизвестным, то фактически мы опять имеем задачу 19, в которой требуется лишь заменить p на p1 и a на 1/b. Условие существования решения в данном случае запишется так:

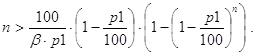
Завершая рассмотрение предложенного цикла задач, отметим, что большая часть из них допускает то или иное естественное обобщение и развитие.

Заключение

Рассмотрение затронутой в этой работе проблемы сейчас очень актуально, поэтому необходимо создание эффективных методик решения практических задач именно с помощью рекурсии, как одного из самых простых, понятных и наглядных методов решения задач. Реализация же рекурсивных алгоритмов в любой вычислительной среде достаточно очевидна, поэтому составление обучающих программ, реализация их в виде Web-узла и публикация их в Internet является очень полезным делом по вышеизложенным причинам. Продолжая освоение рекурсии в рамках данного или иного направления нелишне помнить слова выдающегося математика и педагога Д. Пойа [12, c.13]: “Решение задач - практическое искусство, подобное плаванию, катанию на лыжах или игре на фортепиано; научиться ему можно, только подражая хорошим образцам и постоянно практикуясь. … Помните: если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их! ”. В вопросах освоения рекурсии именно так и нужно поступать. Только подражая хорошим образцам и постоянно практикуясь, можно освоить рекурсивный метод решения прикладных задач.

Литература

1.      Симонов А.С. Экономика на уроках математики. М.: Школа-Пресс, 1999.

2.      Борохов Э. Энциклопедия афоризмов (Мысль в слове). М.: изд. АСТ, 1999.

3.      Дорофеев Г.В., Седова Е.А. Процентные вычисления. СПб.: Специальная литература, 1997.

4.      Доллан Э.Д., Линдсей Д.Б. Рынок. Макроэкономическая модель. СПб., 1992.

5.      Макконнелл К.Р., Брю С.Л. Экономикс. Т.1,2. М.: Республика, 1993.

6.      Самуэльсон П. Экономика. Т.1,2. М.: Алгон, 1992.

7.      Фишер С. и др. Экономика. М.: Алгон, 1992.

8.      Ланкастер П. Теория матриц. М.: Наука, 1978.

9.      Беллман Р. Введение в теорию матриц. М.: Наука, 1969.

10.    Добровольский Н.М., Есаян А.Р., Пихтильков С. A., Стеценко В.Я. Об одном вычислительном эксперименте. Межвузовский сборник статей. Ч.1-Тула: Изд-во Тул. гос. пед. ун-та, 1999.10 с.

11.    Есаян А.Р. Фракталы и рекурсия. Учеб. пособие для студентов педвузов. - Тула, 1999. -52с.

12.    Пойа Д. Математическое открытие. Решение задач: основные понятия, изучение и преподавание. М.: Наука, 1970.

13.    Беккенбах Э., Беллман Р. Неравенства. М.: Мир, 1965.

14.    Вайскопф Дж. Microsoft FrontPage 2000: учебный курс - СПб.: Питер, 2000.