Содержание
Задание 1
Задание 2
Использованная литература
Приложение
Задание 1
Таблица 1
Исходные данные
| потребительские расходы | среднемесячная номинальная начисленная заработная плата | |
| Белгородская область | 4678,7 | 8428,1 |
| Брянская область | 4464,1 | 6385,7 |
| Владимирская область | 3386,2 | 7515,5 |
| Воронежская область | 4913,2 | 6666,7 |
| Ивановская область | 3592 | 6545,2 |
| Калужская область | 5900,4 | 8483,8 |
| Костромская область | 3925 | 7492,4 |
| Курская область | 4992,4 | 7150,6 |
| Липецкая область | 5385,3 | 8617,1 |
| Московская область | 9030,4 | 11752,4 |
| Орловская область | 4338 | 6786,6 |
| Рязанская область | 4406,1 | 7763,1 |
| Смоленская область | 5128,7 | 7827,6 |
| Тамбовская область | 5196 | 6267,5 |
| Тверская область | 5875,9 | 8115,1 |
| Тульская область | 4464,8 | 7723,3 |
| Ярославская область | 5265,1 | 9012,8 |
| г.Москва | 22024,2 | 18698,6 |
По исходным данным выполнить корреляционный анализ:
1.1. Построить корреляционное поле и предложить гипотезу о связи исследуемых факторов;
1.2. Определить коэффициенты корреляции;
1.3. Оценить статистическую значимость вычисленных коэффициентов корреляции
1.4. Сделать итоговые выводы
Решение 1. Построение поля корреляции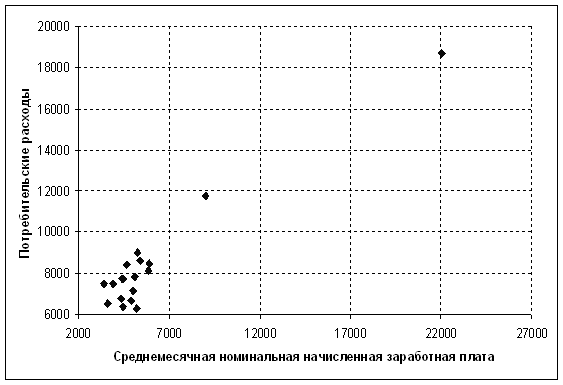
Рис. 1. Поле корреляции
По полю корреляции можно сделать вывод о прямолинейной связи между потребительскими расходами и среднемесячной номинальной начисленной заработной платой
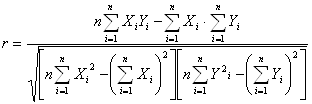
2. Расчет коэффициента корреляцииДля определения коэффициента корреляции может быть использована встроенная функция (=КОРРЕЛ(B4:B21;C4:C21)).
![]()
Так как коэффициент корреляции находится в диапазоне от 0,9 и более. То связь между потребительскими расходами и среднемесячной номинальной начисленной заработной платы весьма тесная
3. Оценка статистической значимости коэффициента корреляцииОценку статистической значимости коэффициента корреляции проведем с помощью t-статистики Стьюдента.
Выдвигаем гипотезу Н0 о статистически незначимом отличии показателей от нуля а0=а1=rху=0.
tтабл для числа степеней свободы df=n-2=18-2=16 и a=0,05 составит 2,12.
Расчетный коэффициент Стьюдента находятся по формуле:
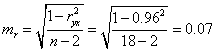
![]()
Фактические значения t-статистики превосходят табличное значение на 5% -м уровне значимости при числе степеней свободы 16, tтабл = 2,12. Таким коэффициент корреляции является статистически значимым Гипотеза Н0 не принимается.
Рассчитаем доверительный интервал:![]()
![]() Таким образом, с вероятностью 95% можно утверждать, что коэффициент корреляции находится в диапазоне от 0,81 до 1.
Таким образом, с вероятностью 95% можно утверждать, что коэффициент корреляции находится в диапазоне от 0,81 до 1.
Связь между потребительскими расходами и среднемесячной номинальной начисленной заработной платой прямолинейная и весьма тесная, это можно заключить исходя из распределения фактических значений по полю корреляции и расчетного значения коэффициента корреляции
Так как коэффициент корреляции находится в диапазоне от 0,9 и более, то связь между потребительскими расходами и среднемесячной номинальной начисленной заработной платы весьма тесная.
Коэффициент корреляции является статистически значимым с вероятностью 95% можно утверждать, что он находится в диапазоне от 0,81 до 1.
Задание 2
Таблица 3
Исходные данные
| № п/п | Чистый доход, млрд долл. США, у | Рыночная капитализация компании, млрд долл. США, х4 |
| 1 | 0,9 | 40,9 |
| 2 | 1,7 | 40,5 |
| 3 | 0,7 | 38,9 |
| 4 | 1,7 | 38,5 |
| 5 | 2,6 | 37,3 |
| 6 | 1,3 | 26,5 |
| 7 | 4,1 | 37 |
| 8 | 1,6 | 36,8 |
| 9 | 6,9 | 36,3 |
| 10 | 0,4 | 35,3 |
| 11 | 1,3 | 35,3 |
| 12 | 1,9 | 35 |
| 13 | 1,9 | 26,2 |
| 14 | 1,4 | 33,1 |
| 15 | 0,4 | 32,7 |
| 16 | 0,8 | 32,1 |
| 17 | 1,8 | 30,5 |
| 18 | 0,9 | 29,8 |
| 19 | 1,1 | 25,4 |
| 20 | 1,9 | 29,3 |
| 21 | -0,9 | 29,2 |
| 22 | 1,3 | 29,2 |
| 23 | 2 | 29,1 |
| 24 | 0,6 | 27,9 |
| 25 | 0,7 | 27,2 |
По исходным данным выполнить регрессионный анализ:
2.1. Рассчитать параметры уравнения линейной парной регрессии;
2.2. Дать с помощью общего (среднего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом;
2.3. Оценить качество уравнения с помощью средней ошибки аппроксимации.
2.4. Оценить статистическую надежность результатов регрессионного моделирования с помощью критерия Стъюдента и F-критерия Фишера.
2.5. Сделать итоговые выводы.
Решение 1. Расчет параметров уравнения линейной парной регрессииЛинейная модель: ![]()
Расчеты для определения параметров модели произведены в Microsoft Exel.
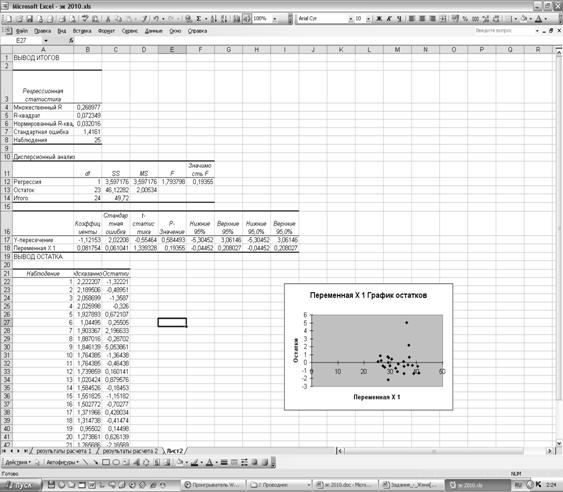
Рис. 2.1. Результаты регрессионного анализа
В результате расчетов получаем уравнение регрессии:
![]()
При росте рыночной капитализации компании на 1 млр. руб. чистый доход возрастает на 0,0818 млрд. руб.
2. Расчет общего (среднего) коэффициента эластичностиКоэффициент эластичности будем находить по следующей формуле:
![]()
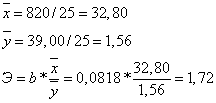
Э=1,72 показывает, что чистый доход возрастает на 1,72% при росте рыночной капитализации компании на 1%.
3. Оценка качества уравнения с помощью средней ошибки аппроксимацииСредняя ошибка аппроксимации находится как средняя арифметическая простая из индивидуальных ошибок по формуле:
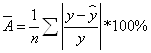
![]()
Расчетные значения в среднем отличаются от фактических на 59%. Так как средняя ошибка аппроксимации превышает 10%, то полученную модель нельзя считать точной.
4. Оценить статистическую надежность результатов регрессионного моделирования с помощью критерия Стъюдента и F-критерия Фишера![]()
Так как значение коэффициента корреляции до 0,3 , то связь между чистым доходом и рыночной капитализацией компании слабая.
Оценку статистической значимости параметров регрессии проведем с помощью t-статистики Стьюдента.
Выдвигаем гипотезу Н0 о статистически незначимом отличии показателей от нуля а0=а1=rху=0.
tтабл для числа степеней свободы df=n-2=25-2=23 и a=0,05 составит 2,07.
Расчетные коэффициенты Стьюдента в Excel:
![]()
Фактические значения t-критерия меньше табличного значение на 5% -м уровне значимости при числе степеней свободы 23, tтабл = 2,07. Таким образом коэффициенты статистическим не значимы. Гипотеза Н0 принимается.
Коэффициент детерминации равен квадрату коэффициента линейной корреляции
![]()
7% вариации чистого дохода объясняется вариацией рыночной капитализацией компании. А 93% вариацией других неучтенных факторов.
Критерий F-Фишера:
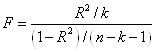
Табличное значение F- критерия при доверительной вероятности 0,95 при V1=k=1 и V2=n-k-1=25-1-1=23 составляет Fтабл =4,28.
![]()
Поскольку Fрас<Fтабл., то уравнение регрессии является не адекватным.
5. ВыводыУравнение линейной однофакторной зависимости рыночной капитализации компании от чистого дохода имеет вид: ![]()
Это означает, что при росте рыночной капитализации компании на 1 млр. руб. чистый доход возрастает на 0,0818 млрд. руб. Согласно расчету коэффициента эластичности чистый доход возрастает на 1,72% при росте рыночной капитализации компании на 1%.
Так как средняя ошибка аппроксимации превышает 10% (59%>10%), то полученную модель нельзя считать точной.
Значение коэффициента корреляции до 0,3 , то связь между чистым доходом и рыночной капитализацией компании слабая.
Параметры регрессии статистически не значимы. 7% вариации чистого дохода объясняется вариацией рыночной капитализацией компании. А 93% вариацией других неучтенных факторов. Поскольку Fрас<Fтабл., то уравнение регрессии является не адекватным.
Использованная литература
1. Арженовский С.В., Федосова О.Н. Эконометрика: Учебное пособие/Рост, гос. экон. унив. - Ростов н/Д., - 2002.
2. Орлов А.И. Эконометрика: Учебник . – М.: Экзамен, 2002.
3. Практикум по эконометрике: Учебник /Под ред. И.И.Елисеевой. – М.: Финансы и статистика, 2003.
4. Федосеев В.В. и др. Экономико-математические методы и прикладные модели. М.: ЮНИТИ, 2001
5. Холод Н.И. Экономико-математические методы и модели. М.: 2003.
6. Эконометрика Учебное пособие /И.И. Елисеева. С.В. Курышева, Д.М. Гордиенко и др. - М.: Финансы и статистика, 2001.
7. Эконометрика: Учебник /Под ред. И.И.Елисеевой. – М.: Финансы и статистика, 2002.
Приложение
Значение t-критерия Стьюдента при уровне значимости 0,10, 0,05, 0,01
| Число степеней свободы | Р | ||
| 0,10 | 0,05 | 0,01 | |
| 1 | 6,3138 | 12,706 | 63,657 |
| 2 | 2,9200 | 4,3027 | 9,9248 |
| 3 | 2,3534 | 3,1825 | 5,8409 |
| 4 | 2,1318 | 2,7764 | 4,6041 |
| 5 | 2,0150 | 2,5706 | 4,0321 |
| 6 | 1,9432 | 2,4469 | 3,7074 |
| 7 | 1,8946 | 2,3646 | 3,4995 |
| 8 | 1,8595 , | 2,3060 | 3,3554 |
| 9 | 1,8331 | 2,2622 | 3,2498 |
| 10 | 1,8125 | 2,2281 | 3,1693 |
| 11 | 1,7959 | 2,2010 | 3,1058 |
| 12 | 1,7823 | 2,1788 | 3,0545 |
| 13 | 1,7709 | 2,1604 | 3,0123 |
| 14 | 1,7613 | 2,1448 | 2,9768 |
| 15 | 1,7530 | 2,1315 | 2,9467 |
| 16 | 1,7459 | 2,1199 | 2,9208 |
| 17 | 1,7396 | 2,1098 | 2,8982 |
| 18 | 1,7241 | 2,1009 | 2,8784 |
| 19 | 1,7291 | 2,0930 | 2,8609 |
| 20 | 1,7247 | 2,0860 | 2,8453 |
| 21 | 1,7207 | 2,0796 | 2,8314 |
| 22 | 1,7171 | 2,0739 | 2,8188 |
| 23 | 1,7139 | 2,0687 | 2,8073 |
| 24 | 1,7109 | 2,0639 | 2,7969 |
| 25 | 1,7081 | 2,0595 | 2,7874 |
| 26 | 1,7056 | 2,0555 | 2,7787 |
| 27 | '1,7033 | 2,0518 | 2,7707 |
| 28 | 1,7011 | 2,0484 | 2,7633 |
| 29 | 1,6991 | 2,0452 | 2,7564 |
| 30 | 1,6973 | 2,0423 | 2,7500 |
| 40 | 1,6839 | 2,0211 | 2,7045 |
| 60 | 1,6707 | 2,0003 | 2,6603 |
| 120 | 1,6577 | 1,9799 | 2,6174 |
|
| 1,6449 | 1,9600 | 2,5758 |
Значение F-критерия Фишера при уровне значимости 0,05
| V2 | V1 | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 1 | 161 | 200 | 216 | 225 | 230 | 234 | 237 | 239 |
| 2 | 18,51 | 19,00 | 19,16 | 19,25 | 19,30 | 19,33 | 19,36 | 19,37 |
| 3 | 10,13 | 9,55 | 9,28 | 9,19 | 9,01 | 8,94 | 8,88 | 8,84 |
| 4 | 7,71 | 6,94 | 6,59 | 6,39 | 6,26 | 6,16 | 6,09 | 6,04 |
| 5 | 6,61 | 5,79 | 5,41 | 5,19 | 5,05 | 4.95 | 4,88 | 4,82 |
| 6 | 5,99 | 5,14 | 4.76 | 4.53 | 4,39 | 4,28 | 4,21 | 4,15 |
| 7 | 5,59 | 4,74 | 4,35 | 4,12 | 3,97 | 3,87 | 3,79 | 3,73 |
| 8 | 5,32 | 4,46 | 4,07 | 3,84 | 3,69 | 3,58 | 3,50 | 3,44 |
| 9 | 5,12 | 4,26 | 3,86 | 3,63 | 3,48 | 3,37 | 3,29 | 3,23 |
| 10 | 4,96 | 4,10 | 3,71 | 3,48 | 3,33 | 3,22 | 3,14 | 3,07 |
| 11 | 4,84 | 3,98 | 3,59 | 3,36 | 3,20 | 3,09 | 3,01 | 2,95 |
| 12 | 4,75 | 3,88 | 3,49 | 3,26 | 3,11 | 3,00 | 2,92 | 2,85 |
| 13 | 4,67 | 3,80 | 3,41 | 3,18 | 3,02 | 2,92 | 2,84 | 2,77 |
| 14 | 4,60 | 3,74 | 3,34 | 3,11 | 2,96 | 2,85 | 2,77 | 2,70 |
| 15 | 4,54 | 3,68 | 3,29 | 3,06 | 2,90 | 2,79 | 2,70 | 2,64 |
| 16 | 4,49 | 3,63 | 3,24 | 3,01 | 2,85 | 2,74 | 2,66 | 2,59 |
| 17 | 4,45 | 3,59 | 3,20 | 2,96 | 2,81 | 2,70 | 2,62 | 2,55 |
| 18 | 4,41 | 3,55 | 3,16 | 2,93 | 2,77 | 2,66 | 2,58 | 2,51 |
| 19 | 4,38 | 3,52 | 3,13 | 2,90 | 2,74 | 2,63 | 2,55 | 2,48 |
| 20 | 4,35 | 3,49 | 3,10 | 2,87 | 2,71 | 2,60 | 2,52 | 2,45 |
| 21 | 4,32 | 3,47 | 3,07 | 2,84 | 2,68 | 2,57 | 2,49 | 2,42 |
| 22 | 4,30 | 3,44 | 3,05 | 2,82 | 2,66 | 2,55 | 2,47 | 2,40 |
| 23 | 4,28 | 3,42 | 3,03 | 2,80 | 2,64 | 2,53 | 2,45 | 2,38 |
| 24 | 4,26 | 3,40 | 3,01 | 2,78 | 2,62 | 2,51 | 2,43 | 2,36 |
| 25 | 4,24 | 3,88 | 2,99 | 2,76 | 2,60 | 2,49 | 2,41 | 2,34 |
| 26 | 4,22 | 3,37 | 2,98 | 2,74 | 2,59 | 2,47 | 2,39 | 2,32 |
| 27 | 4,21 | 3,35 | 2,96 | 2,73 | 2,57 | 2,46 | 2,37 | 2,30 |
| 28 | 4,20 | 3,34 | 2,95 | 2,71 | 2,56 | 2,44 | 2,36 | 2,29 |
| 29 | 4,18 | 3,33 | 2,93 | 2,70 | 2,54 | 2,43 | 2,35 | 2,28 |
| 30 | 4,17 | 3,32 | 2,92 | 2,69 | 2,53 | 2,42 | 2,34 | 2,27 |
| 35 | 4.12 | 3.26 | 2.87 | 2.64 | 2.48 | 2.37 | 2.28 | 2.22 |
| 40 | 4,08 | 3,23 | 2,84 | 2,61 | 2,45 | 2,34 | 2,25 | 2,18 |
| 50 | 4,03 | 3,18 | 2,79 | 2,56 | 2,40 | 2,29 | 2,20 | 2,13 |
| 60 | 4,00 | 3,15 | 2,76 | 2,52 | 2,37 | 2,25 | 2,17 | 2,10 |
| 100 | 3,94 | 3,09 | 2,70 | 2,46 | 2,30 | 2,19 | 2,10 | 2,03 |
Похожие работы
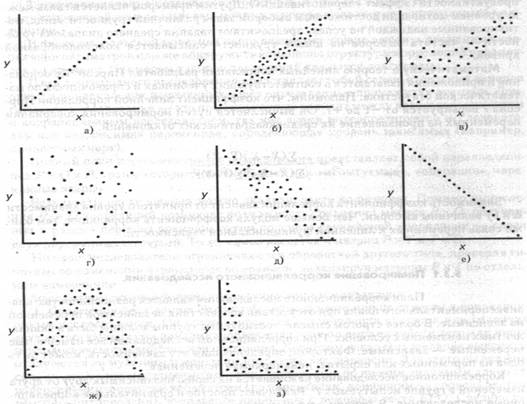
... а) строгая положительная корреляция, б) сильная положительная корреляция, в) слабая положительная корреляция, г) нулевая корреляция, д) отрицательная корреляция, е) строгая отрицательная корреляция, ж) нелинейная корреляция, з) нелинейная корреляция. 3. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ Корреляционный анализ (от лат. «соотношение», «связь») применяется для проверки гипотезы о статистической зависимости ...
... изменения другого. Корреляционная зависимость - это изменения, которые вносят значения одного признака в вероятность появления разных значений другого признака (Е.В. Сидоренко, 2000). Задача корреляционного анализа сводится к установлению направления (положительное или отрицательное) и формы (линейная, нелинейная) связи между варьирующими признаками, измерению ее тесноты, и, наконец, к ...
имического региона (СБГХР). Целью данной работы явилось определение корреляционной взаимосвязи морфологических структур сосудов плацент жительниц СБГХР Кадамджая, а также проживающих в территориальной близости. Материал и методы. Объектом исследования явились 142 плаценты рожениц (средний возраст 25,8 лет) после естественного родоразрешения (39-41нед). Исследуемый материал был распределен на 3 ...
... Составляющие магнитного поля. // Солнечно-земная физика. 2-я часть. М.: «Мир» — 1974. —с. 96-99. 11. С.-И. Акасофу, C. Чепмен. Геомагнитные индексы. // Солнечно-земная физика. 2-я часть. М.: «Мир» — 1974. —с. 293-301. 12. А.М. Грецкий,Н.Н. Евсюков. Корреляционный анализ солнечно-земных связей.//Астрофизические приложения методов теории случайных функций. Харьков ХГУ 1988 —с.10-14. 13. И.П. ...
0 комментариев