Методы внутренней сортировки
Основные понятия и методы сортировки
Сортировка – это процесс расстановки элементов «в некотором порядке». Элементы размещаются так, чтобы, во-первых, вычисления требующие определенного порядка расположения данных, могли выполняться эффективно, во-вторых, результаты имели осмысленный вид, в третьих, последующие процессы бы пригодные исходные данные.
Записи, поля и ключи. Единица данных, типично обрабатываемая информационными системами, называется записью. Запись – это совокупность элементов информации о каком-то событии или структуре. Каждый элемент информации в записи, такой как номер служащего, цена единицы товара или валовой объем, называется полем записи. Совокупность полей идентифицирует и описывает то, что представлено в записи. Из записей составляются файлы или наборы данных. Сортировка является процессом перестановки записей или их индексов, при котором их взаимное расположение в файле приводиться в порядок, определяемый некоторым известным ключом. Ключом называется поле, содержащее величину, используемую в правилах упорядочивания файла.
В предположении, что результатом сортировки является физическое упорядочивание, сортировка двух записей в своей простейшей форме состоит из сравнения их ключевых полей и определений, которое из них «меньше». После этого записи переставляются так, что запись с «меньшим» ключом ставиться перед записью с «большим» ключом.
Определить, какой ключ «меньше», можно, используя любое правило. Очевидными правилами являются: алфавитное упорядочивание, числовое и буквенно-цифровое. (В последнем правиле ключи могут содержать смесь букв и цифр; соглашения, принятые в системе, определяют упорядочение букв и цифр.)
Ключом записи может быть одно поле или комбинация полей, распределенных по записи. Если ключ состоит из нескольких несоприкасающихся полей, то он называется составным ключом.
Иногда желательно упорядочение внутри упорядочивания. Например, файл может быть упорядочен по номеру места работы, а внутри этого упорядочения – по номеру служащего. Поле, содержащее номер места работы, называется старшим ключом, а поле, содержащее номер служащего, – младшим ключом. Так модно определить несколько уровней ключей, и все уровни, отличные от первого, называются младшими ключами. Старший и младший ключи можно рассматривать как один составной ключ в записи.
В информационной системе иногда удобно, чтобы файлы упорядочивались не единственным способом. Различные сортировки в качестве ключа могут использовать различные поля.
Запись может состоять только из поля ключа. В обработке научных приложений это не является чем-то исключительным. В данной работе при рассмотрении методов сортировки будет предполагаться, что записи состоят из одного поля. Это сделано для того, чтобы упростить первоначальное представление о методах сортировки за счет устранения побочных проблем, возникающих при перемещении данных. Поскольку эти методы одинаково хорошо применимы к записям, содержащим как ключевые, так и неключевые поля, то это предположение не ограничивает общности.
Традиционно методы сортировки делят на внутренние и внешние. Внутренние методы – это такие методы, которые могут применяться с приемлемой производительностью только к тем спискам данных, которые целиком помещаются в основной (оперативной) памяти процессора. Внешние методы – это такие методы, которые приемлемы для файлов данных, которые слишком велики, чтобы поместится в основной памяти, и поэтому должны в течение процесса сортировки располагаться на устройствах внешней памяти (лентах, дисках, барабанах). Слово список часто обозначает набор записей, расположенных в основной памяти.
Линейный выбор с обменом: использование обменов
В качестве примера обмена в процессе сортировки рассмотрим здесь минимальную по памяти версию линейного выбора. Обменом называется перестановка позиций двух записей в списке в зависимости от результата проверки их относительной величины. Если в списке встречается запись с ключом, меньшим, чем у предыдущей, то эти записи меняются местами. Производительность методов обмена зависит от сложности определения последовательности сравнений и обменов. Часто число обменов сокращают, откладывая обмен до конца каждого просмотра. Это прием, в частности, используется в методе, который будет описан ниже.
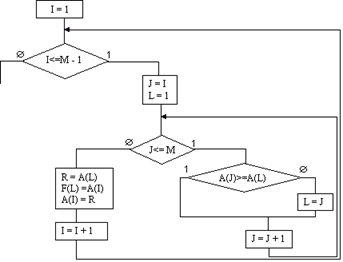
Линейный выбор с обменом. В начале первого просмотра предполагается, что первый элемент списка имеет наименьший ключ. Этот ключ вместе с адресом пересылается в рабочую память, где сравнивается со всеми линейными преемниками до тех пор, пока не встретится меньший ключ. Меньший ключ и его адрес становятся содержимым рабочей области памяти.
Сравнения продолжаются при новом содержимом рабочей памяти. Пересылка выполняется всегда, когда в списке встречается ключ, который меньше ключа в рабочей памяти. Таким образом, в рабочей памяти всегда расположен наименьший из уже просмотренных ключей. Просмотр заканчивается по достижении конца списка. До этого момента процесс идентичен простому линейному выбору. Сортировка обменом отличается следующим шагом.
По окончании первого просмотра запись, ключ которой расположен в рабочей памяти, переставляется с записью из вершины списка. Теперь наименьшая величина в списке занимает первую позицию. Второй просмотр идентичен первому с той лишь разницей, что вторым по величине считается второй ключ, так как первым стоит наименьший элемент. Первая позиция исключается из процесса. По окончании второго просмотра вторая запись с наименьшим ключом помещается во вторую позицию списка. Третий просмотр начинается сравнением ключа из третьей позиции и т.д. Эта процедура заканчивается, когда свое место занимает (N – 1) – я запись.
алг Sort (арг цел N, вещ таб A [1:N])
нач цел i, j, k, Maxi
нц для i от N до 2 шаг -1
Maxi:= i;
нц для j от 1 до i – 1
Если A[j] >A[Maxi]
то Maxi:= j;
все
Если Maxi <> i
то k:= A[i];
A[i]:= A[Maxi];
A[Maxi]:= k;
все
кц
кон
Оценим количество сравнений. При первом просмотре их N – 1, при втором – N – 2, при последнем – 1. Общее количество C = N –1 + N – 2 + …+ 1 = C = N × (N – 1)/2, то есть имеет порядок O(N2).
Линейный выбор с подсчетом
Метод сортировки с подсчетом описывается в литературе как процедура упорядочения внутреннего списка чисел. Фактически, это не метод сортировки, а технический прием, который можно использовать в различных методах для сокращения количества обменов или полного их устранения. Он является формой индексирования, в которой счетчик относительной позиции каждого элемента корректируется в течение процесса сравнения. Ниже будет описан этот технический прием применительно к линейному выбору.
Подсчет как технический прием. Память, используемая линейным выбором с подсчетом, будет включать область вывода (так же как и при линейном выборе) для хранения окончательно упорядоченного списка. Размер области вывода отвечает тем же соображениям, что и при линейном выборе. Дополнительно должна быть обеспечена память под счетчик для каждого элемента списка. В результате действий над значениями этих счетчиков образуется множество индексов позиций для элементов в упорядоченном списке. При каждом просмотре ключ сравнивается со своими линейными преемниками. Каждый раз, когда находится больший ключ, его счетчик увеличивается на единицу. Если найденный ключ меньше или равен, то увеличивается счетчик соответствующий большему из сравниваемому ключей. Следовательно, в любой момент времени счетчик элемента указывает количество ключей, о которых известно, что они меньше ключа рассматриваемого элемента.
При первом просмотре первый ключ в списке сравнивается со всеми остальными ключами. В его счетчике подсчитывается количество меньших ключей. В счетчиках больших ключей будут 1. При втором просмотре первый ключ не рассматривается. Второй ключ сравнивается с ключами всех преемников. Подсчеты фиксируются. Этот процесс продолжается N – 1 раз. На этом этапе известно относительная позиция каждого элемента. Помещая ключи в выходной список в соответствии со значениями их счетчиков, получаем упорядоченный список.
алг Sort (арг цел N, цел таб A [1:N], рез цел таб B [1:N]);
нач цел i, j, цел таб Count [1:N]
нц для i от N до 2 шаг -1
нц для j от i – 1 до 1 шаг -1
Если A[i] < A[j]
то Count [j]:= Count [j] + 1
иначе Count [i]:= Count [j]+1
все
кц
кц
нц для i от 1 до N
B [Count [i] + 1]:= A[i]
кц
кон
Число сравнений равно N2/2. Выполняется (N-1) просмотров с N/2 сравнениями в среднем на каждом просмотре. Значение счетчиков изменяется столько раз, сколько раз выполняется сравнение.
Сортировка обменом
Сортировка обменом – это общий термин, используемый для описания семейства минимальных по памяти методов сортировки, которые меняют местами элементы списка, если предшествующий элемент больше последующего. Просмотр файла может протекать сверху вниз или снизу вверх или изменяться от просмотра к просмотру.
Существует ряд определенных вариантов, которые различаются последовательностями сравнений элементов списка. Во всех элементарных методах обмена элемент сравнивается со своим ближайшим соседом, а возможными перемещениями являются перемещение элемента с большим ключом на одну позицию вниз и перемещение элемента с меньшим ключом на одну позицию вверх. Парный обмен, стандартный обмен и просеивание являются тремя простыми формами сортировки обменом.
Метод парного обмена (также называемый «нечетно-четная перестановка») состоит из различного числа «нечетных» и «четных» просмотров. При нечетных просмотрах каждый элемент из нечетной позиции сравнивается со своим соседом из четной позиции и больший из них занимает большую позицию. Нисходящий просмотр списка продолжается до тех пор, пока последний нечетный элемент (N – 1) в списке не сравнивается с последним четным элементом N. Если в списке нечетное число элементов, то последний элемент не будет участвовать в сравнении. В течение каждого просмотра ведется подсчет обменов.
При четных просмотрах четные позиции сравниваются с соседними нечетными. Обмены выполняются тогда, когда надо, чтобы больший из пары занял нечетную позицию. Таким образом, ключи с большими значениями перемещаются на дно списка. При этом должно быть столько просмотров, сколько необходимо для того чтобы переместить в позицию число, наиболее удаленное от своей конечной позиции. Затем выполняется заключительный просмотр, необходимый для того, чтобы опознать упорядоченность. В течение этого просмотра счетчик обменов равен 0. Данный метод требует, по крайней мере, двух просмотров – одного нечетного и одного четного.
Метод стандартного обмена (также называемый «методом пузырька») перемещает один элемент списка в соответствующую позицию при каждом просмотре. Таким образом, при первом просмотре запись с наибольшим ключом помещается в последнюю позицию, при втором просмотре запись со следующим по величине ключом перемещается в предпоследнюю позицию и т.д. Метод может быть преобразован так, что будет размещать элементы по убыванию.
При первом просмотре первый элемент списка сравнивается со своим непосредственным преемником, и, если этот преемник меньше, они меняются местами. Теперь больший элемент, расположенный во второй позиции, сравнивается с элементом из третьей позиции. Обмен происходит, если необходимо больший из них разместить в третьей позиции. Затем позиция 3 сравнивается с позицией 4, позиция 4 с позицией 5 и т.д. когда позиция N – 1 сравнивается с позицией N, просмотр заканчивается.
Если в списке элемент k – 1 расположен раньше чем k, то при каждом сравнении (k – 1): k больший элемент попадает в позицию k. Элемент, перемещаемый вниз, считается в данный момент наибольшим в списке. Когда при сравнении обнаруживается, что k-й элемент больше, обмен не происходит. Следовательно, каждый раз сравниваются элемент, считающийся наибольшим (k – 1), и его непосредственный преемник k.
Второй просмотр идентичен первому с той лишь разницей, что уже установленная позиция исключается из последовательности. Каждый последующий просмотр исключает очередную установленную позицию, укорачивая список.
Подсчет обменов ведется для каждого просмотра. Просмотр, в результате которого число обменов не увеличилось, заканчивает сортировку.
алгSort (арг цел N, цел таб A [1:N])
нач цел k, i, w
нц для k от N до N – 1
нц для i от 1 до N – k
если A[i] > A [i + 1]
то w:= A[i]
A[i]:= A [i + 1]
A [i + 1]:= w
все
кц
кц
кон
При сортировке «методом пузырька» выполняется N – 1 просмотр, причем на i – м просмотре производится N – i сравнений. Общее количесво сравнений C = N × (N – 1)/2, то есть имеет порядок O(N2).
Метод просеивания (также называемый «линейной вставкой с обменом» или «челночной сортировкой») является самым лучшим из этих методов. Он отличается от других методов обмена тем, что не сохраняет фиксированной последовательности сравнений. Кроме этого, исчезает разделение на отдельные просмотры как следствие схемы последовательностей сравнений. Метод просеивания работает точно так же, как стандартный обмен до тех пор, пока не надо выполнять перестановку. Сравниваемая величина с меньшим ключом поднимается насколько это возможно вверх по списку. Она сравнивается «в обратном порядке» со всеми ее линейными предшественниками по направлению к вершине списка. Если ее ключ меньше, чем у предшественника, то выполняется обмен и начинается очередное сравнение. Когда элемент, передвигаемый вверх, встречается с меньшим ключом, этот процесс прекращается и нисходящие сравнения возобновляются с той позиции, с которой выполнялся первый обмен.
Будем называть нисходящее сравнение первичным, а восходящее вторичным. Любое первичное сравнение может увеличить число вторичных сравнений. Если первичное сравнение охватывает позиции 6 и 7, то цепочка вторичных сравнений может иметь самое большее 5 сравнений. Этот максимум достигается, если исходный ключ из позиции 7 меньше всех ключей в списке, расположенных выше этой позиции. Фактическая длина последовательности вторичных сравнений зависит от величины двигающегося вверх элемента относительно величины каждого элемента из предшествующей упорядоченной части списка.
Сортировка заканчивается, когда первичное сравнение охватит (N + 1) – й элемент.
Сортировка вставками
Сортировка вставками есть общее название группы методов сортировки, основанных на последовательной вставке «новых» элементов в увеличивающийся упорядочиваемый список. Среди них есть три существенно разных метода: линейная вставка, центрированная вставка и двоичная вставка. Эти методы сортировки различаются методами поиска подходящего места для вставки элемента. Простейшим методом является линейная вставка. Как следует из названия, в этом методе уже существующий список рассматривается как простой линейный список, просматриваемый поэлементно сверху вниз, пока не будет найдена соответствующая позиция для нового элемента.
Этот метод обычно используется тогда, когда процесс, внешний к данной сортировке, динамически вносит добавление в список, все элементы которого известны и который должен все время поддерживаться в упорядоченном состоянии. Сортировка выполняется каждый раз при получении нового элемента, размещая этот элемент в нужное место списка и облегчая контроль. Некоторые характеристики систем реального времени делают вставку полезным техническим приемом.
Связь между процессом, порождающим подлежащие сортировке числа, и сортировкой такова, что сортировка привлекается многократно. Такое повторное привлечение может быть сопряжено с некоторыми издержками, такими как передача параметров, вход и выход из процедуры. Эти издержки должны быть выявлены и учтены при анализе использования метода вставок таким способом. Сортировку вставками можно организовать как один унифицированный процесс.
Метод линейной вставки. Под сортировку выделяется количество памяти, равное предполагаемой длине окончательного списка из всех элементов. Счетчик длины списка в самом начале устанавливается равным нулю. При помощи этого счетчика контролируется длина области поиска нужной позиции для элемента, вставляемого в список. Сортировка привлекается для каждого элемента. Один «вызов» сортирующей подпрограммы размещает один элемент в списке и увеличивает счетчик списка на единицу.
Первый элемент помещается в верхнюю позицию области вывода. Следующий элемент, присоединяемый к списку, сравнивается с первым. Если ключ нового элемента больше, он помещается в позицию, следующую за позицией первого элемента. Если ключ нового элемента меньше, то первый элемент перемещается в позицию 2, а новый элемент помещается в позицию 1.
В дальнейшем все новые элементы последовательно сравниваются с каждым элементом списка, начиная с первого, до тех пор, пока не встретиться больший. Этот больший элемент и все последующие элементы списка передвигаются на одну позицию вниз. Таким образом освобождается место, на которое вставляется новый элемент.
Метод сортировки Шелла
Сортировка Шелла является расширением сортировки просеиванием. Последний просмотр в сортировке Шелла идентичен методу просеивания, описанному выше. Предшествующие просмотры используют тот же технический прием, но в них сравниваются и обмениваются не непосредственные соседи, а элементы отстоящие на заданное расстояние. Например, позиция 1 сравнивается с позицией 5, позиция 5 с позицией 9, 9 с 13 и т.д. Когда обнаружена инверсия, цепочка вторичных сравнений охватывает те элементы, которые входили в последовательность первичных сравнений. Например, если обнаружена инверсия между позициями 9 и 13, то возможная вторичная последовательность состоит из сравнений 5: 9 и 1: 5.
На каждом просмотре шаг между сравниваемыми элементами определяется путем сокращения вычисленного исходного шага. На последнем просмотре он сокращается до 1. Цель метода на ранних просмотрах – сократить число вторичных сравнений и обменов на более поздних просмотрах. В этом методе элементы могут совершать большие скачки к нужным позициям на ранних просмотрах, а не передвигаться на одну позицию за один раз. На последнем просмотре числа будут стремиться располагаться близко к своим позициям и, следовательно, потребуют незначительных перемещений при окончательном размещении.
Модификации метода различаются способами вычисления начального шага между элементами и правилами сокращения этого шага от просмотра к просмотру.
Вариант с отложенными обменами
При описании метода сортировки Шелла предполагалось, что обмен следует за каждым сравнением, которое выявляет элемент больший, чем предыдущий элемент части. В алгоритме (опубликованном Хиббардом) использован метод, сокращающий число обменов. Этот алгоритм отличается то ранее описанного тем, что он использует временную память для хранения сравниваемых элементов в течение всей последовательности сравнений.
Каждое первичное сравнение Ключi: ключi +шаг включает пересылку ключi +шаг во временную память. Сравнение позиции 1 с позицией 4, например, на самом деле включает пересылку из позиции 4 во временную память и сравнение ключа из временной памяти с ключом из позиции 1. Если ключi больше, он перемещается в позицию ключi +шаг. Если ключi +шаг больше, то перемещение не нужно. Пересылка во временную память позволяет эффективно освобождать позицию последующего элемента этой части.
Когда ключi больше, чем ключi +шаг, то ключi пересылается из своей позиции в «свободную» позицию, и метод начинает последовательность вторичных сравнений. Содержимое временной памяти (ключi +шаг) – это запись, поднимающаяся на верх данной части. Ключ каждой записи сравнивается с временной памятью и, если обнаружено, что он больше, пересылается вниз списка в текущую свободную позицию. Каждая пересылка освобождает позицию перемещенного элемента. Когда в списке обнаружен элемент с ключом, меньшим ключа временной памяти, содержимое временной памяти помещается в позицию списка освобожденной самой последней, т.е. в нужное место.
Использование временной памяти эффективно тогда, когда длина последовательности вторичных сравнений не меньше 2. Поскольку, скорее всего это верно для списков произвольной конечной длины со случайно упорядоченными данными, то вариант с отложенными обменами может, вообще говоря, быть лучше других сортировок Шелла.
Быстрая сортировка
Метод быстрой сортировки был впервые описан Ч.А.Р. Хоаром В 1962 году. Быстрая сортировка – это общее название ряда алгоритмов, которые отражают различные подходы к получению критичного параметра, влияющего на производительность метода.
Метод быстрой сортировки. Некоторый элемент списка выбирается в качестве «основы». Все элементы, меньше основы, размещаются в позициях с начала списка»; все элементы, больше основы, размещаются в позициях с конца списка. Элементы сравниваются с основой и изменяют свою позицию, когда они больше и расположены в писке выше нее, или когда меньше и расположены в списке ниже нее. Это упорядочение составляет этап сортировки. В конце этапа для размещения основы пригодна некоторая позиция в списке. Эта позиция соответствует месту основы в окончательном списке, поскольку ее относительный адрес в списке определяется числом элементов выше и ниже нее.
Этап определяет две части. Если значение основы хорошо аппроксимирует медиану списка, то эти две части будут примерно равной длины. Если основа является наихудшей возможной оценкой медианы (наибольшим или наименьшим элементом списка), то эти части будут длиной 0 и К – 1, где К – это длина исходного списка.
Способ построения частей, по существу, один и тот же во всех версиях алгоритма. Устанавливаются два указателя, один на начало, другой на конец списка. После выбора основы поиск меньшей величины начинается с указателя конца, перемещающегося вверх к началу списка. Сравнения продолжаются до тех пор, пока не будет найден элемент, меньший основы, или не будет исчерпан список.
Когда элемент, меньшей основы, найден, его необходимо переместить в позицию, содержащий элемент, большей основы. Эта позиция находится при сравнениях, использующих указатель начала. Сравнения выполняются сверху в низ по списку до тех пор, пока указатель начала не укажет на больший элемент. Таким образом, элементы, больший и меньший основы, идентифицированы, и теперь выполняется обмен между ними.
Модификации возникают только в методе пересылки элементов данных. Один способ состоит в том, что основа пересылается во временную память, а содержимое начала списка перемещается в освободившуюся позицию. При этом освобождается начальная позиция, куда можно переместить элемент. После пересылки свободная позиция сдвигается в ячейку, расположенную близко к концу списка. При нисходящем поиске отыскивается элемент для пересылки в эту свободную позицию. Свободная позиция чередуется с верхней и нижней позициями до тех пор, пока указатели не совместятся.
После обмена или двойной пересылки возобновляется поиск другого элемента, меньшего основы. Когда он найден, начинается поиск большего элемента с использованием указателя начала. Этот процесс продолжается до тех пор, пока два указателя не встретятся. Относительная длина частей определяется позицией в списке, в которой совместятся указатели начала и конца. В некоторых версиях этого метода необходимо сравнивать относительные позиции указателей после каждого перемещения по списку вверх или вниз.
На первом этапе строятся две части. Одна из них используется в качестве исходной на втором этапе, вторая помещается в стек LIFO. Общее правило таково: первой обрабатывать меньшую часть, а границы большей запоминать в стеке. Второй этап порождает две части. Меньшая обрабатывается на третьем этапе, а большая перемещается в стек над большей частью, построенной на этапе 1. Процесс порождения частей, запоминания большей из них в стеке и разделения меньшей продолжается до тех пор, пока все части не сократятся до одного элемента. При возникновении одноэлементной части новая часть для стека не строится. Ожидающие части выбираются из стека и обрабатываются. Сортировка выполнена, когда стек пуст.
Обработка меньшей из двух частей гарантирует, что ожидающих частей в стеке будет не более log2N. Последовательность обработки частей совершенно произвольна и может изменяться по желанию программиста.
Быстрая сортировка может использоваться в комбинированном алгоритме, чтобы сократить части до заранее определенного размера, после чего они упорядочиваются другим методом, более эффективным для малых списков.
Алг QuickSort (арг цел m, t)
нач цел i, j, x, w
i:= m
j:= t
x:= div (A (m + t), 2)
нц
нц пока A[i] < x
i:=i+1
кц
нц пока A[j] > x
j:=j-1
кц
если i <= j
то
w:= A[i]
A[i]:= A[j]
A[j]:= w
i:= i+1
j:= j-1
все
кц пока i > j;
если m < j
то QuickSort (m, j);
все
если i < t
то QuickSort (i, t);
все
кон
Оценим эффективность метода. Предположим, что размер массива равен числу, являющемуся степенью двойки, и при каждом разделении элемент X находится точно в середине массива. В этом случае при первом просмотре выполняется N сравнений и массив разделяется на две части размерами » N/2 сравнений и т.д. следовательно,
C = N + 2 × (N / 2) + 4 × (N / 4) + … + N × (N / N) = O(N ×log2N).
Внутреннее слияние
Основой процесса слияния является фундаментальная идея упорядочения данных путем чередования элементов из двух или более упорядоченных списков. Упорядоченное объединение этих списков представляет собой окончательный упорядоченный список из десяти элементов. Сравниваются наименьшие элементы каждой части и меньшей из них продвигается в список вывода. Процесс сравнения элементов, продвижения меньшего в список вывода и выбор преемника в «победившей» части продолжается до тех пор, пока не исчерпывается одна из частей. После того как одна часть исчерпана, все оставшиеся элементы другой пересылаются в список вывода.
Алг Sl (арг цел k, m, q, цел таб A [1:N])
нач цел k, i, j, t, цел таб A [1:N]
i:= k
j:= m +1
t:= 1
нц пока (i <= m) и (j <= q)
если A[i] <= A[j] то
D[t]:= A[i]
i:= i +1
иначе
D[t]:= A[j]
j:= j +1
t:= t +1
все
кц
нц пока i = m
D[t]:= A[i]
i:= i +1
t:= t +1
нц пока j:= q
D[t]:= A[j]
j:= j +1
t:= t +1
кц
кц
нц для i от 1 до t – 1
A [k + i – 1]:= D[i]
кц
кон
Эффективность алгоритма составляет C = O (N×log2N).
Похожие работы
... показал, что при правильно подобранных t и h сложность алгоритма Шелла является O(n(1.2)), что существенно меньше сложности простых алгоритмов сортировки. 3. Обменная сортировка Простая обменная сортировка (в просторечии называемая "методом пузырька") для массива a[1], a[2], ..., a[n] работает следующим образом. Начиная с конца массива сравниваются два соседних элемента (a[n] и a[n-1]). ...
... памяти ЭВМ, то его упорядочение называют внутренним. Если для хранения упорядочиваемых данных используются внешнее запоминающее устройство, то такое упорядочение называют внешним. Критериями оценки методов сортировки являются: С - количество операций сравнения пар ключей, Р - число перестановок элементов , S - резерв памяти. Среднее количество операций сравнения зависит от ...
... ключ массива. Сторожевые элементы повсеместно используются в ситуациях подобных этой для предотвращения дополнительной проверки (в данном случае j>0), что почти всегда помогает во внутренних циклах. Пузырьковая сортировка Элементарный метод сортировки, который часто дают на вводных занятиях – это пузырьковая сортировка: Стоящие рядом элементы массива обмениваются местами, до тех пор, пока ...
... не повторяются. Простой путь – путь, в котором дуги не повторяются. Маршрут – последовательность ребер, составляющих, как и путь, цепочку. Длина пути взвешенного графа определяется как сумма весов – его дуг. Если граф не взвешен, то можно считать веса дуг равными 1. Кратчайшим путем между выделенной парой вершин хн и хк называется путь, имеющий наименьшую длину среди всех возможных путей между ...
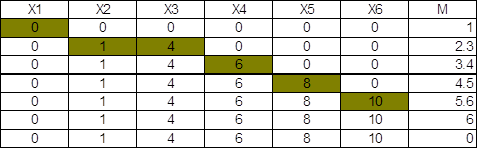
0 комментариев