Методы синтеза и оптимизации

МИHИСТЕРСТВО ОБРАЗОВАHИЯ И НАУКИ УКРАИHЫ

ДОHБАССКАЯ ГОСУДАРСТВЕHHАЯ МАШИHОСТРОИТЕЛЬHАЯ АКАДЕМИЯ

Кафедра компьютерных информационных технологий

 

Контрольная работа №1, 2

по дисциплине

«Методы синтеза и оптимизации»

Выполнила

студентка группы ИТ 99-1з Александрова А.Н

Проверила

Веремей О.В.

Краматорск 2002

Задание 1

 

ПРОГРАММИРОВАНИЕ ЧИСЛЕННЫХ МЕТОДОВ ОДНОМЕРНОЙ ОПТИМИЗАЦИИ

Цель задания: закрепить теоретические сведения и приобрести практические навыки разработки алгоритмов и программ для нахождения экстремальных значений функции одной переменной методом перебора с применением ЭВМ.

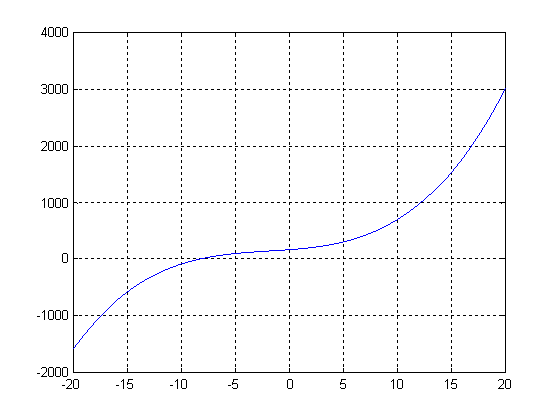
Найти максимум и минимум функции при изменении аргумента от -4 до 3 с точностью 0,0001. Функция достигает максимума при меньших значениях аргумента. Постройте график функции.

Исходные данные приведены в таблице 1.

Таблица 1

Номер варианта	A	B	С	D
6	1,5	0,4	-5,6	-10,8

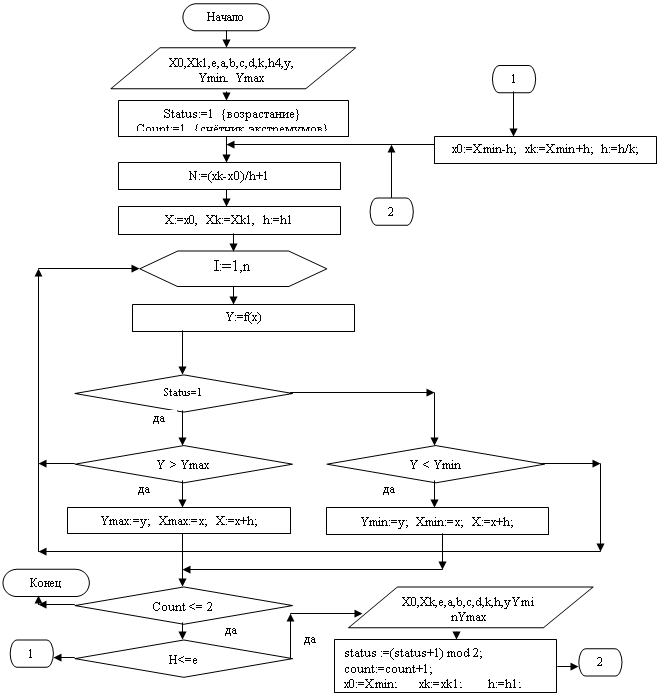
Рисунок 1 – блок-схема метода

Решение задачи на ЭВМ с графиком исследуемой функции

На рисунке 2 изображено решение задачи на ЭВМ с графиком функции.

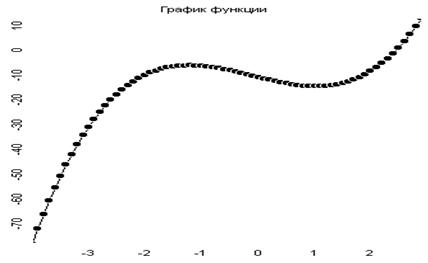
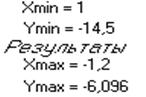
Рисунок 2- результаты работы программы, график функции

Краткие выводы по работе

Задача решена методом последовательного равномерного перебора с уточнением, т.е. вначале проводится поиск с большим шагом, а при нахождении экстремума поиск повторяется в зоне экстремума с уменьшенным шагом.

Программа реализующая алгоритм

:

procedure TForm1.SpeedButton1Click(Sender: TObject);

var a,b,c,d,e,y,Ymax,Xmax,

 x0,X,Xk,Xmin,Ymin,h,k :real;

 i,n,count :integer;

 status :integer; // 0-убывание, 1-возрастание

label l1;

Function MOO(x:real):real;

 begin

 result:=a*x*x*x + b*x*x + c*x + d;

 end;

begin

 Form1.Series1.Clear;

 try // ввод начальных условий

 with form1 do

 begin

 LabelXmin.Caption:='Xmin = 0';

 LabelYmin.Caption:='Ymin = 0';

 LabelXmax.Caption:='Xmax = 0';

 LabelYmax.Caption:='Ymax = 0';

 end;

 a:=strtofloat(form1.Edit1.Text);

 b:=strtofloat(form1.Edit2.Text);

 c:=strtofloat(form1.Edit3.Text);

 d:=strtofloat(form1.Edit4.Text);

 e:=strtofloat(form1.Edit5.Text);

 h:=strtofloat(form1.Edit6.Text);

 x0:=strtofloat(form1.Edit7.Text);

 xk:=strtofloat(form1.Edit8.Text);

 k:=10;

 Ymin:=1000000000;

 Ymax:=-10000000000;

 status:=1;

 count:=1;

 except

 showMessage('Неправильно введены начальные условия');

 end;

l1: n:=trunc((xk-x0)/h)+1;

 x:=x0;

 for i:=1 to n do

 begin

 y:=MOO(x);

 case status of

 0: if y<Ymin then

 begin

 Ymin:=y;

 Xmin:=x;

 X:=x+h;

 end;

 1: if Y>Ymax then

 begin

 Ymax:=y;

 Xmax:=x;

 X:=x+h;

 end;

 end;

 end;

 if count <= 2 then

 if h <= e then

 begin

 with form1 do // вывод результата

 begin

 LabelXmin.Caption:='Xmin = '+floatTostr(Xmin);

 LabelYmin.Caption:='Ymin = '+floatTostr(Ymin);

 LabelXmax.Caption:='Xmax = '+floatTostr(Xmax);

 LabelYmax.Caption:='Ymax = '+floatTostr(Ymax);

 end;

 status :=(status+1) mod 2; //Следующий экстремум

 count:=count+1;

 x0:=Xmin;

 xk:= strtofloat(form1.Edit8.Text);

 h:=strtofloat(form1.Edit6.Text);

 goto l1;

 end

 else

 begin

 x0:=Xmin-h;

 xk:=Xmin+h;

 h:=h/k;

 goto l1;

 end;

 x:=strtofloat(form1.Edit7.Text);

 while x < strtofloat(form1.Edit8.Text) do

 begin

 y:=MOO(x);

 form1.Series1.AddXY(x,y);

 x:=x+0.1;

 end;

end;

Задание 2

РЕШЕНИЕ ОДНОМЕРНЫХ ЗАДАЧ ОПТИМИЗАЦИИ МЕТОДАМИ ПОСЛЕДОВАТЕЛЬНОГО ПОИСКА

 

Цель задания: приобрести практические навыки разработки алгоритмов и программ для решения одномерных задач оптимизации методами последовательного поиска: дихотомии и золотого сечения.

Индивидуальное задание

Найти минимум функции f(x) на промежутке [a,b] с точностью . Исходные данные и номера вариантов приведены в таблице 2. Построить график минимизируемой функции.

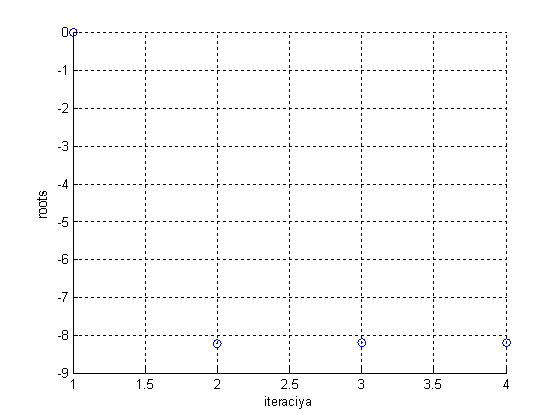
Найдите минимум функции  на промежутке [a,b] c точностью ε = 10^-4 , методом «золотого сечения»постройте график минимизируемой функции.

Блок-схема метода «Золотого сечения» представлена на рисунке3.

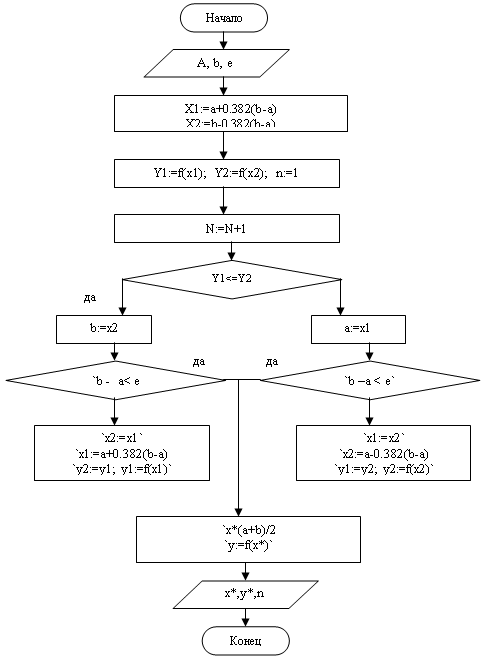
Рисунок 3 – Блок-схема метода «Золотого сечения»

На рисунке 4 изображено решение задачи на ЭВМ и график минимизируемой функции.

Вывод: Методы последовательного поиска строятся в предположении унимодальности функции на заданном интервале. Исходя из свойств, унимодальности строится такая стратегия последовательного поиска экстремальной точки Х*, при которой любая пара вычислений f(x) позволяет сузить область поиска (интервал неопределённости).

Процедура минимизации функции:

procedure TForm1.SpeedButton2Click(Sender: TObject);

label l2;

Var a,b,e,x,x1,x2,y,y1,y2,Xmin,Ymin :real ;

 n :integer;

 t:string;

Function f(x:real):real;

 begin

 f:=tan(x)+exp(-x)+x;

 { f:=x*x+sin(x);}

 end;

 begin

 Form1.Series1.Clear;

 try // ввод начальных условий

 a:=strtofloat(form1.Edit9.Text);

 b:=strtofloat(form1.Edit10.Text);

 e:=strtofloat(form1.Edit11.Text);

 except

 showMessage('Неправильно введены начальные условия');

 end;

 x1:=a+0.382*(b-a); x2:=b-0.382*(b-a);

 y1:=f(x1); y2:=f(x2);

 n:=1;

l2: n:=n+1;

 if y1<= y2 then

 begin

 b:=x2;

 if (b-a) >= e then

 begin

 x2:=x1;

 x1:=a+0.382*(b-a);

 y2:=y1;

 y1:=f(x1);

 goto l2;

 end;

 end

 else

 begin

 a:=x1;

 if (b-a)>=e then

 begin

 x1:=x2;

 x2:=b-0.382*(b-a);

 y1:=y2;

 Y2:=f(x2);

 goto l2;

 end;

 end;

 Xmin:=(a+b)/2;

 Ymin:=f(Xmin);

 str(Xmin:10:4,t);

 form1.Label20.Caption:='Xmin = '+t;

 str(Ymin:10:4,t);

 form1.Label21.Caption:='Ymin = '+t;

 form1.Label22.Caption:='n = '+Inttostr(n);

 x:=strtofloat(form1.Edit9.Text);

 while x < strtofloat(form1.Edit10.Text) do

 begin

 y:=f(x);

 form1.Series1.AddXY(x,y);

 x:=x+0.1;

 end;

end;

Задание 3

 

ГРАДИЕНТНЫЕ МЕТОДЫ РЕШЕНИЯ МНОГОМЕРНЫХ ЗАДАЧ ОПТИМИЗАЦИИ

Цель задания: закрепить теоретические сведения и приобрести практические навыки поиска безусловного экстремума функции многих переменных градиентным методом.

Индивидуальное задание

Найдите минимум функции  методом наискорейшего спуска, выбрав начальную точку .Дать геометрическую иллюстрацию решения задачи.

Решение

1) В точке  f(X₀) = = -14,5

Вычислим координаты градиента функции в точке Х₀ :

.

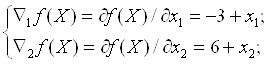
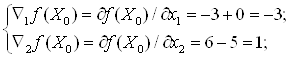
Поскольку , то Х₀ не является точкой экстремума

2) Переместимся изХ⁰ вдоль градиента -  в новую точкуХ₁ по формуле:

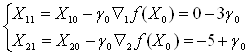
т.е. .

Для определения координат точки Х₁ нужно выбрать значение шага . Получим :

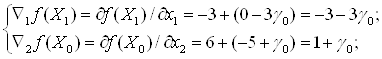
Из соотношения (,)=0 имеем:

(-3-3)(-3)+(1+)=10+10=0

откуда =

Задание 4

 

ПРИМЕНЕНИЕ ГРАДИЕНТНЫХ МЕТОДОВ ДЛЯ ОПТИМИЗАЦИИ НА ЭВМ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ОБЪЕКТОВ

 

Цель задания: приобрести практические навыки разработки алгоритмов и программ оптимизации математических моделей градиентным методом.

 Индивидуальное задание

Найдите минимум функции f(x1,х2) методом наискорейшего спуска, выбрав в качестве начальной точки сначала Хо, а затем точку из противоположного квадраниа. Сравните число итераций. Для определения оптимального шага путём одномерной минимизации вдоль антиградиентного направления примите метод дихотомии в программе, предусмотрите отрисовку траектории наискорейшего спуска.

, при Хо(2,4).

Блок-схема алгоритма решения изображена на рисунке 5

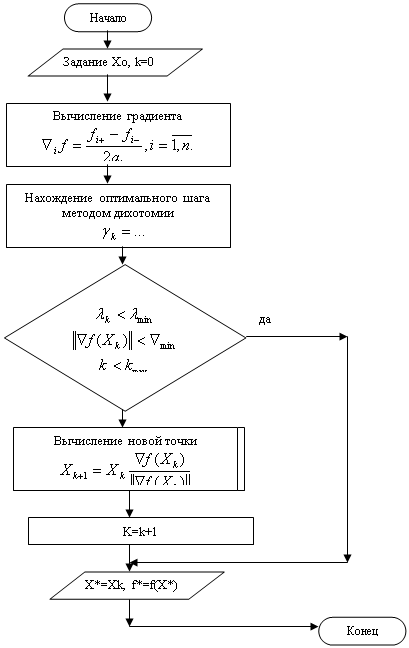
Рисунок 5- блок-схема алгоритма решения методом наискорейшего спуска

Результаты работы программы.

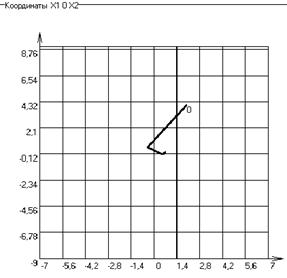
Рисунок 6- Решение задачи на ЭВМ и траектория поиска оптимальных значений (при Хо(2,4))

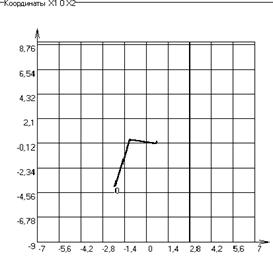
Рисунок 7 Решение задачи на ЭВМ и траектория поиска оптимальных значений (при Хо(-2,-4))

Вывод: Особенностью метода наискорейшего спуска является то, что поиск решения выполняется с оптимальным шагом, который рассчитывается с помощью одномерной минимизации функции. Градиенты в двух соседних точках ортогональны и поэтому траектория к оптимальному решению в виде зигзага с поворотом под прямым углом. При Хо(2,4) количество итераций – 5, а при Хо(-2,-4) количество итераций уменьшилось до 4,а значение целевой функции осталось прежним – F(x)=0,61370564. Листинг подпрограммы метода.

unit Opt1_4;

interface

uses

 Messages, SysUtils, Graphics, Forms, Dialogs;

 const n=2;

 type Artype =array[1..n] of real;

 Funop=function(xi:Artype):real;

 ProcMin=Procedure(a,b,e:real; var xm,ym:real);

type

 TForm2 = class(TForm)

 private

 public

 procedure Optimiz(k: integer);

 end;

var

 Form2: TForm2;

 Nmax,prn,NN:integer;

 e,Fopt:real;

 X0,G:artype;

 f1:funop;

 Pmin:ProcMin;

 kAntGrad:real;

function model1(x: Artype): real;

implementation

 uses Main,UnitGraph;

 // Подпрограмма вычисления заданной функции

function model(x:Artype):real;

 begin

 model:= exp(x[1])+sqr(x[2])-2*x[1];

 end;

 {main program}

procedure Grad(n: integer; e: real; x: artype; var g: Artype;

 F: Funop);

 Var i:integer; fp,fo:real;

 begin

 for i:=1 to n do

 begin

 x[i]:=x[i]+e;

 fp:=F(x);

 x[i]:=x[i]-2*e;

 fo:=F(x);

 x[i]:=x[i]+e;

 g[i]:=(fp-fo)/2/e;

 end;

end;

procedure Opgrad(n: integer; e: real; var xk: Artype; Nmax: integer;

 prn: byte; var Fopt: real; var nn: integer; F: Funop);

 Label 1;

 Var dk:Artype;//Градиент

 od{норма вектор-градиента},

 lambda{шаг},s,sf:real;

 i:integer;

 Function FF(x:real):real;

 Var i:integer;

 begin

 for i:=1 to n do

 xk[i]:=xk[i]+abs(x)*dk[i]/od;

 FF:=F(xk);

 for i:=1 to n do

 xk[i]:=xk[i]-abs(x)*dk[i]/od;

 end;

 Procedure Min(a0,b0,e:real; Var xm,ym:real);// Метод Дихотомии

 Label 1,2;

 Var x1,x2,y1,y2,delta,a,b:real;

 k,n:integer;

 begin

 a:=a0; b:=b0;

 delta:=e/2;

1: n:=2*k;

 x1:=(a+b-delta)/2;

 x2:=(a+b+delta)/2;

 y1:=ff(x1); y2:=ff(x2);

 if y1<=y2 then b:=x2

 else a:=x1;

 if (b-a)<e then

 begin

 xm:=(a+b)/2;

 ym:=ff(xm);

 end

 else

 begin

 k:=k+1;

 goto 1

 end;

end;

 {main prcvedure}

 BEGIN

 nn:=0; lambda:=0;

 if prn=0 then

 begin

 for i:=1 to n do

 form1.ListBox1.Items.Add('x'+inttostr(i)+'='+Floattostr(xk[i])+' ');

 form1.ListBox1.Items.Add(#13 + 'Целевая функция = '+ Floattostr(F(xk))+#13);

 end;

 repeat

 Grad(n,e/2,xk,dk,F);

 for i:=1 to n do

 dk[i]:=-dk[i]; sf:=F(xk);

 if prn=1 then

 begin

 form1.ListBox1.Items.Add('Итерация №'+inttostr(nn)+ #13 +' Шаг = '+Floattostrf(lambda,ffGeneral,8,5) );

 form1.ListBox1.Items.Add('Текущая точка ');

 for i:=1 to n do

 begin

 form1.ListBox1.Items.Add('X'+inttostr(i)+'='+floattostrf(xk[i],ffGeneral,8,5));

 formGraph.imGraph.Canvas.LineTo(round( mx* xk[1]+ Sx),round( -my* xk[2]+ Sy));

 end;

 form1.ListBox1.Items.Add(#13+'Текущий антиградиент');

 for i:=1 to n do

 form1.ListBox1.Items.Add('g'+inttostr(i)+'='+Floattostrf(dk[i],ffGeneral,8,5)+' ');

 form1.ListBox1.Items.Add(' Целевая функция F = '+Floattostrf(sf,ffGeneral,8,5));

 form1.ListBox1.Items.Add('-------------------------------------------');

 end;

 od:=0;

 for i:=1 to n do

 od:=od+sqr((dk[i]));

 od:=sqrt(od); if od<e then goto 1;

 nn:=nn+1;

 if nn>Nmax then

 begin

 nn:=nn-1;

 showmessage('Минимум не найден !!!'+ #13+' Необходимое числоитераций больше выделенного ресурса'+Inttostr(Nmax));

 Fopt:=F(xk);

 Exit

 end;

 Min(0,10,e,lambda,s);

 for i:=1 to n do

 xk[i]:=xk[i]+lambda*dk[i]/od;

 Until(lambda<e);

1: Fopt:=F(xk);

with form1.ListBox1.Items do

 begin

 Add(' Оптимальные значения за '+inttostr(nn)+' итерации');

 for i:=1 to n do

 Add('X'+inttostr(i)+'*'+'='+floattostrf(xk[i],ffGeneral,8,5));

 Add(' Целевая функция F(X*) = '+Floattostrf(fopt,ffGeneral,8,5));

 end;

end;

function model1(x: Artype): real;

begin

end;

procedure TForm2.Optimiz(k: integer);

begin

 try // ввод начальных условий

 with form1 do

 begin

 X0[1]:=strtofloat(form1.Edit12.Text);

 X0[2]:=strtofloat(form1.Edit13.Text);

 end

 except

 showMessage('Неправильно введены начальные условия');

 end;

 with FormGraph do //координатная плоскость

 begin

 {Установка максимума и минимума функции}

 Xb:=-abs(X0[1])-5; Xe:=abs(X0[1])+5; Ymin:=-abs(X0[2])-5;Ymax:=abs(X0[2])+5;

 GrafOrt;

 end;

 Nmax:=500; e:=0.00001;prn:=1;

 formGraph.imGraph.Canvas.Pen.Color:=clRed;

 formgraph.imGraph.Canvas.Pen.Width:=2;

 formgraph. imGraph.Canvas.TextOut(round( mx* x0[1]+ Sx),

 round( -my* x0[2]+ Sy),'0');

 formGraph.imGraph.Canvas.MoveTo(round( mx* x0[1]+ Sx),round( -my* x0[2]+ Sy));

 F1:=Model;

 Grad(n,0.1,X0,g,f1);

 Opgrad(n,e,X0,Nmax,prn,fopt,NN,f1);

 formgraph.imGraph.Canvas.Pen.Width:=1;

end;

end.

Задание 5

 

МЕТОДЫ НУЛЕВОГО ПОРЯДКА РЕШЕНИЯ МНОГОМЕРНЫХ ЗАДАЧ ОПТИМИЗАЦИИ

Цель задания: приобрести практические навыки разработки алгоритмов и программ оптимизации многомерных функций методами ненулевого порядка, в частности методом прямого поиска.

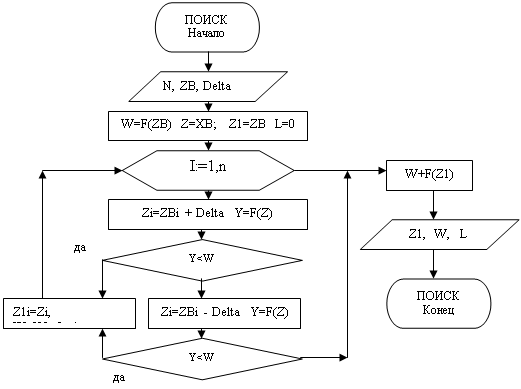
Рисунок 8 – блок-схема подпрограммы циклического изменения координат базисной точки

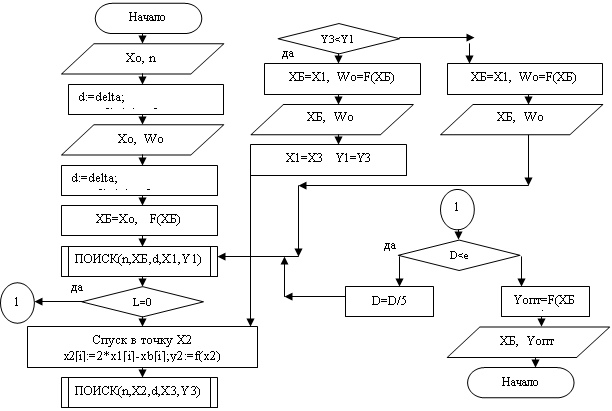
Рисунок 9 – Блок-схема метода прямого поиска

Индивидуальное задание.

Найдите минимум функции  методом прямого поиска, выбрав в Хо(3, -1, 2), а потом Хо(-3, 1, -2).

Алгоритм с помощью которого проводилась оптимизация функции изображена на рисунках 8, 9 в виде блок-схем.

Решение задачи на ЭВМ.

На рисунках 10, 11 изображены результаты оптимизации на ЭВМ при различных начальных условиях

 

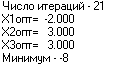
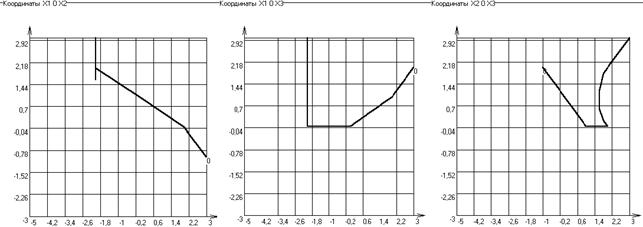
Рисунок 10 – результаты и траектория движения базиса при Хо(3, -1, 2)

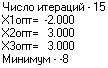
Рисунок 11 – результаты при Хо(-3,1, -2)

 Вывод: В ходе работы при изменении начальных условий было выявлено, что приближение начальных условий к оптимальным значениям количество итераций значительно уменьшается. Листинг подпрограммы

procedure Poisk(n:integer; zb:Artype; delta:real;

 Var z1:Artype; Var w:real;

 Var l:integer; F:Funop);

Var

 z:Artype; i:integer; y:real;

 begin

 w:=f(zb);

 z:=zb; z1:=zb; l:=0;

 for i:=1 to n do

 begin

 z[i]:=zb[i]+delta; y:=f(z);

 if y<w then

 begin

 z1[i]:=z[i]; l:=l+1; w:=y

 end

 else begin

 z[i]:=zb[i]-delta; y:=f(z);

 if y<w then

 begin

 z1[i]:=z[i]; l:=l+1; w:=y

 end

 end;

 end;

 w:=f(z1);

end;

procedure MyClass.OptPoisk(n,m:integer;

 delta,eps:real; xo:Artype; Var xb:Artype;

 Var Yopt:real; Var ip:integer; F:Funop);

Label 6,7,10;

Var x1,x2,x3:Artype;

 d,wo,y1,y2,y3:real; i,l:integer;

 a,b:string;

 Procedure Outt(x:Artype; y:real);

 Var i:integer;

 begin

 for i:=1 to n do

 begin

 str( x[i]:8:3,a); str(y:9:3,b);

 form1.ListBox2.Items.Add('X'+inttostr(i)+'='+a);

 with formgraph do

 begin

 imGraph.Canvas.Pen.Color:=clRed;

 imgraph.Canvas.LineTo(round( mx* x[1]+ Sx),

 round( -my* x[2]+ Sy));

 imGraph1_3.Canvas.Pen.Color:=clBlue;

 imgraph1_3.Canvas.LineTo(round( mx* x[1]+ Sx),

 round( -my* x[3]+ Sy));

 imGraph2_3.Canvas.Pen.Color:=clBlack;

 imgraph2_3.Canvas.LineTo(round( mx* x[2]+ Sx),

 round( -my* x[3]+ Sy));

 end;

 end;

 str(y:9:1,b);

 form1.ListBox2.Items.Add('--------------------- F='+b+'-----------');

end;

 Begin

 f:=model;

 d:=delta;

 wo:=f(xo);

 ip:=0;

 with formGraph do

 begin

 imGraph.Canvas.Pen.Width:=2;

 imGraph1_3.Canvas.Pen.Width:=2;

 imGraph2_3.Canvas.Pen.Width:=2;

 for i:=1 to n do

 begin //Перо в начальную точку

 imGraph.Canvas.TextOut(round( mx* xo[1]+ Sx),

 round( -my* xo[2]+ Sy),inttostr(ip));

 imGraph.Canvas.MoveTo(round( mx* xo[1]+ Sx),

 round( -my* xo[2]+ Sy));

 imGraph1_3.Canvas.TextOut(round( mx* xo[1]+ Sx),

 round( -my* xo[3]+ Sy),inttostr(ip));

 imGraph1_3.Canvas.MoveTo(round( mx* xo[1]+ Sx),

 round( -my* xo[3]+ Sy));

 imGraph2_3.Canvas.TextOut(round( mx* xo[2]+ Sx),

 round( -my* xo[3]+ Sy),inttostr(ip));

 imGraph2_3.Canvas.MoveTo(round( mx* xo[2]+ Sx),

 round( -my* xo[3]+ Sy));

 end;

 end;

 Outt(xo,wo);

 xb:=xo;

10: Poisk(n,xb,d,x1,y1,l,F);

 ip:=ip+1;

 if l=0 then goto 6;

7: for i:=1 to n do

 x2[i]:=2*x1[i]-xb[i];

 y2:=f(x2);

 Poisk(n,x2,d,x3,y3,l,F);

 ip:=ip+1;

 if ip>m then

 begin

 ShowMessage('Число итераций > '+inttostr(m)+#13+'Минимум не найден!!!');

 xb:=x3;

 Yopt:=f(xb);

 Exit

 end;

 if y3<y1 then

 begin

 xb:=x1; wo:=f(xb);

 Outt(xb,wo);

 x1:=x3; y1:=y3;

 goto 7

 end

 else

 begin

 xb:=x1; wo:=f(xb);

 Outt(xb,wo);

 goto 10

 end;

6: if d>=eps then

 begin

 d:=d/5;

 goto 10

 end

 else Yopt:=f(xb);

 form1.ListBox2.Items.Add('Число итераций - '+InttoStr(ip));

 for i:=1 to n do

 begin

 str( xb[i]:8:3,a);

 form1.ListBox2.Items.Add('X'+inttostr(i)+'опт'+'='+a);

 end;

 form1.listbox2.Items.Add('Минимум - '+FloatToStr(opt1_5.Yopt));

 

end;

function model(x:Artype): real;

begin

 model:={25*sqr(x[1]+3)+4*sqr(x[3]-4)+10*sqr(x[1]-x[2])+10;}

 {3*sqr(x[1]-4)+50*sqr(x[2]-3)+16*sqr(x[1]-x[3])+12;}

 16*sqr(x[1]+2)+4*sqr(x[2]-3)+5*sqr(x[3]-x[2])-8;

end;

Задание 6

МЕТОДЫ СЛУЧАЙНОГО ПОИСКА РЕШЕНИЯ МНОГОМЕРНЫХ ЗАДАЧ ОПТИМИЗАЦИИ

Цель задания: приобрести практические навыки поиска на ЭВМ условного экстремума функций многих переменных методом случайного поиска с пересчетом.

Индивидуальное задание.

Найдите минимум функции  методом случайного поиска, выбрав начальной точкой Хо(0, 0, 0) при изменении аргументов Xi в пределах [ai, bi]. Предусмотрите отрисовку поиска минимума в координатах x1Ox2, x1Ox3, x2Ox3.

Проведите сравнительный анализ по числу вычислений функции задавая параметр М=10, 15, 20 при шаге Н=20 и, задавая Н=0,5; 1; 2 при М=15

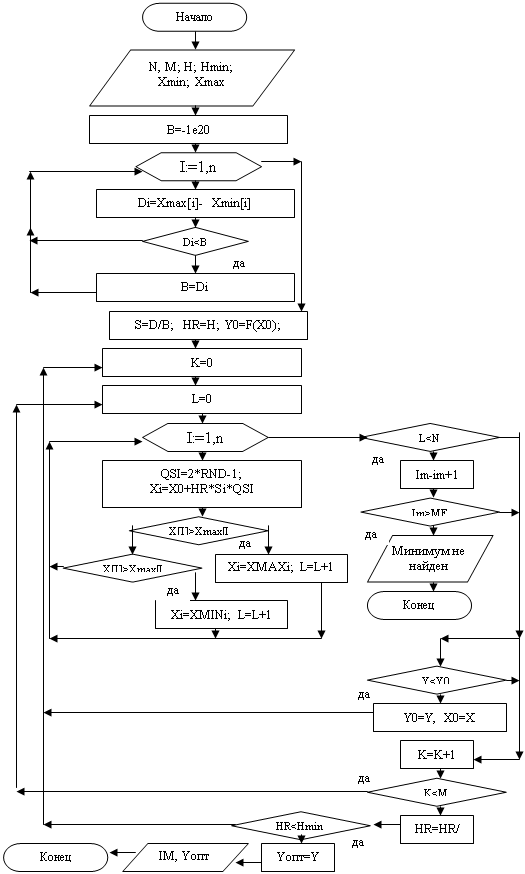
Рисунок 12 – блок-схема метода случайного поиска с перечётом.

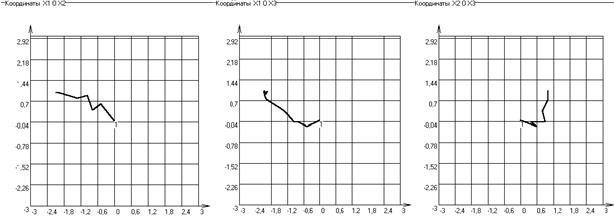
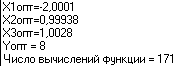
Рисунок 13 решение задачи на ЭВМ и траектория поиска оптимальных значений функции

Результаты работы программы изображены на рисунке 13.

Вывод: в основе метода случайного поиска лежит внесение элементов случая в процедуру формирования пробных точек, которые используются для определения направления поиска. Данный метод эффективен для функций с большим количеством переменных, так как ограничивается количество вычислений функции за счёт нахождения антиградиентного направления с помощью пробных точек.

Листинг подпрограммы метода

unit Opt1_6;

interface

uses

 Dialogs, SysUtils,Graphics;

Const n=3;

Type Artype=array[1..n] of real;

 Funop=function(xi:Artype):real;

type MyClass=class

 public

 procedure slpoisk(n,m,mf:integer;

 h,hmin:real; xmin,xmax:Artype;

 Var xo:Artype; Var Yopt:real; F:Funop);

 end;

var opt6:MyClass;

var

 F:FUNOP;

 i,m,mf,im:integer;

 h,hmin:real;

 xmin,xmax:Artype;

 xo,x:Artype;

 Yopt:real;

function model(x:Artype): real;

implementation

uses main,unitGraph;

function model(x:Artype): real;

begin

 model:={25*sqr(x[1]+3)+4*sqr(x[3]-4)+10*sqr(x[1]-x[2])+10;}

 {10*sqr(x[1]-x[2])+4*sqr(x[1]-2)+25*sqr(x[3]+x[2])+8;}

 16*sqr(x[1]+2)+4*sqr(x[2]-3)+5*sqr(x[3]-x[2])-8;

end;

procedure Myclass.slpoisk(n,m,mf:integer;

 h,hmin:real; xmin,xmax:Artype;

 Var xo:Artype; Var Yopt:real; F:Funop);

 Label 9,10;

 Var x,d,s:Artype; b,hr,y0,y,qsi:real; i,l,k:integer;

 Procedure Outt(x:Artype; y:real; kod:integer);

 Var i:integer;a,b,c:string;

 begin

 for i:=1 to n do

 begin

 str( x[i]:8:3,a); str(y:9:3,b);

 form1.ListBox3.Items.Add('X'+inttostr(i)+

 '='+a);

 if (kod=1) then

 with formgraph do

 begin

 imGraph.Canvas.Pen.Color:=clRed;

 imgraph.Canvas.LineTo(round( mx* x[1]+ Sx),

 round( -my* x[2]+ Sy));

 imGraph1_3.Canvas.Pen.Color:=clBlue;

 imgraph1_3.Canvas.LineTo(round( mx* x[1]+ Sx),

 round( -my* x[3]+ Sy));

 imGraph2_3.Canvas.Pen.Color:=clBlack;

 imgraph2_3.Canvas.LineTo(round( mx* x[2]+ Sx),

 round( -my* x[3]+ Sy));

 end;

 end;

 case Kod of

 0: c:='Начальная точка';

 1: c:='Функция убывает';

 2: c:='Пробнная точка';

 end;

 form1.ListBox3.Items.Add('----------- '+c+' ------'+' F='+b);

end;

 // main

 begin

 f:=model;

 b:=-1e20;

 for i:=1 to n do

 begin

 d[i]:=xmax[i]-xmin[i];

 if d[i]>b then

 b:=d[i];

 end;

 for i:=1 to n do

 s[i]:=d[i]/b;

 hr:=h; y0:=f(xo); im:=1;

 with formGraph do

 begin

 imGraph.Canvas.Pen.Width:=2;

 imGraph1_3.Canvas.Pen.Width:=2;

 imGraph2_3.Canvas.Pen.Width:=2;

 for i:=1 to n do

 begin //Перо в начальную точку

 imGraph.Canvas.TextOut(round( mx* xo[1]+ Sx),

 round( -my* xo[2]+ Sy),inttostr(im));

 imGraph.Canvas.MoveTo(round( mx* xo[1]+ Sx),

 round( -my* xo[2]+ Sy));

 imGraph1_3.Canvas.TextOut(round( mx* xo[1]+ Sx),

 round( -my* xo[3]+ Sy),inttostr(im));

 imGraph1_3.Canvas.MoveTo(round( mx* xo[1]+ Sx),

 round( -my* xo[3]+ Sy));

 imGraph2_3.Canvas.TextOut(round( mx* xo[2]+ Sx),

 round( -my* xo[3]+ Sy),inttostr(im));

 imGraph2_3.Canvas.MoveTo(round( mx* xo[2]+ Sx),

 round( -my* xo[3]+ Sy));

 end;

 end;

 Outt(xo,y0,0);

 randomize;

 9: k:=0;

 10: l:=0;

 for i:=1 to n do

 begin

 qsi:=2*random-1;

 x[i]:=xo[i]+hr*s[i]*qsi;

 if x[i]>xmax[i] then

 begin

 x[i]:=xmax[i]; l:=l+1

 end

 else if x[i]<xmin[i] then

 begin

 x[i]:=xmin[i]; l:=l+1

 end

 end;

 if l<n then

 begin

 y:=f(x);

 outt(x,y,2);

 if y<y0 then outt(x,y,1);

 im:=im+1;

 if im>mf then

 begin

 showMessage('Число вычислений функции > '+IntTostr(mf)+#13+'Минимум не нейден !!!');

 Yopt:=y0;

 Exit

 end;

 if y<y0 then

 begin

 y0:=y;xo:=x;

 goto 9;

 end

 end;

 k:=k+1;

 if k<m then goto 10

 else

 begin

 hr:=hr/2;

 if hr<hmin then

 begin

 Yopt:=y0;

 for i:=1to n do

 form1.ListBox3.Items.Add('X'+inttostr(i)+'опт'+'='+floattostrf(x[i],ffGeneral,5,2)) ;

 form1.ListBox3.Items.Add( 'Yопт = '+floattostrf(Yopt,ffGeneral,5,2));

 form1.ListBox3.Items.Add('Число вычислений функции = '+InttoStr(im)) ;

 Exit end

 else goto 9;

 end;

 end;

end.