Министерство Образования Российской Федерации
Иркутский Государственный Технический Университет.
Кафедра АПП.
Курсовая работа по программированию
и основам алгоритмизации.
Выполнил студент гр.АТП-04-1
Чечев И.С.
Проверила: Пешкова Л.И
Иркутск
2005 г
Вариант 31
Задание 1
1. Проверить условие сходимости и записать расчетные формулы для нахождения корня уравнения ![]() с точностью
с точностью ![]() =
= ![]() методом половинного деления, интервал существования корня [1;2].
методом половинного деления, интервал существования корня [1;2].
Составить блок-схему алгоритма и программу решения задачи. В программе предусмотреть подсчет и вывод на печать числа итерации, за которое удается найти значение корня с заданной точностью. Отладить и выполнить программу на машине.
|
 Блок-схема алгоритма.
Блок-схема алгоритма. ![]()
 Общая:
Общая:
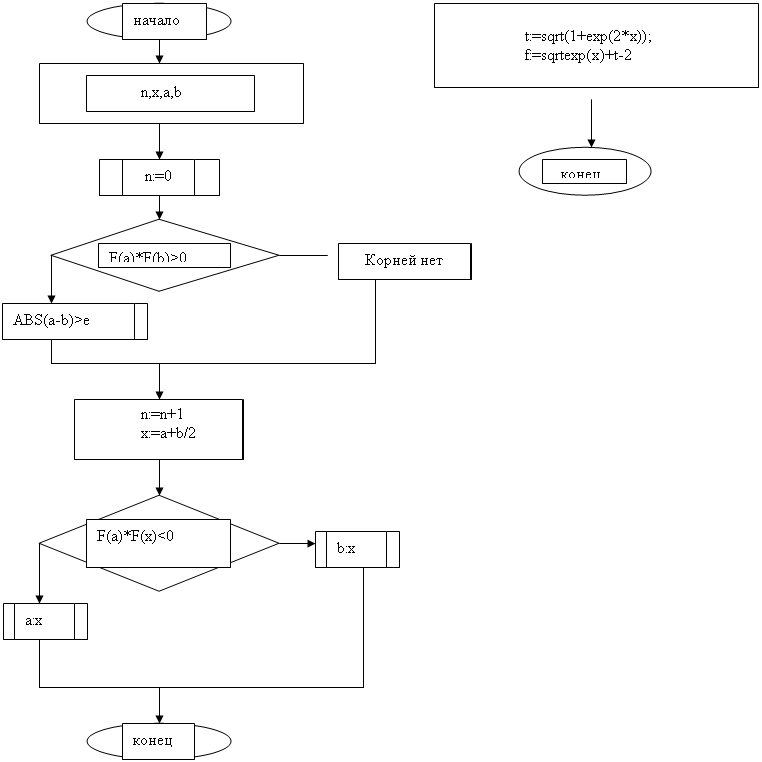
Программа.
Program delenie;
uses crt;
const
e=0.0001
var x,a,b,t:real;
n:integer;
function f(x::real):real;
begin
t:=sqrt(1+exp(2*x));
F:=exp(x)+t-2;
end;
begin
readln(a,b);
n:=0;
if F(a)*F(b)>0 then begin writeln(‘kornei net’); end;
while ABS(a-b)>e do
Begin
n:=n+1;
x:=(a+b)/2
if F(a)*F(x)<0 then b:=x else a:=x;
end;
writeln(‘koren: ‘,x);
writeln(‘chislo iterazii: ‘,n);
end.
Задание 2.
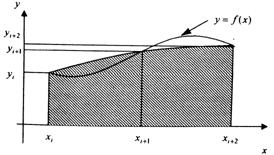
Записать расчетные формулы, составить блок-схему алгоритма и программу для вычисления определенного интеграла ![]() методом Симпсона, разбивая отрезок интегрирования [0;1] на 78 частей. Предусмотреть в программе вычисление точного значения определенного интеграла через первообразную
методом Симпсона, разбивая отрезок интегрирования [0;1] на 78 частей. Предусмотреть в программе вычисление точного значения определенного интеграла через первообразную ![]() .
.
Решение.
Вытекает из формулы Симпсона 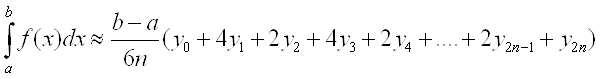
Блок-схема алгоритма.
Function p(x:real):real
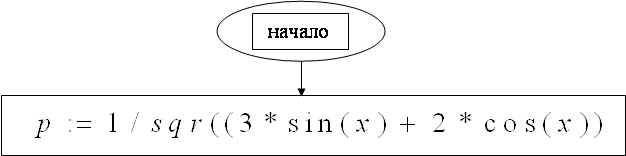 | |||
 | |||
 Function y(x:real):real;
Function y(x:real):real;
| |||
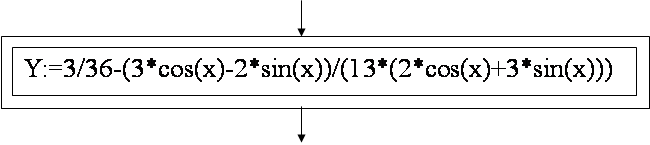 | |||

Основная блок-схема:
![]()

![]()
![]()
![]()
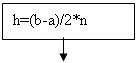
![]()
![]()
![]()
![]()
|
|
|
|
|
|
|
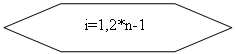
|
Программа.
Program Simpson;
var x,s,h,z,a,b:real;
n,c:integer;
i,k:integer;
function p(x:real):real;
begin
p:=1/sqr(3*sin(x)+2*cos(x));
end;
function y(x:real):real;
begin
y:=3/36-(3*cos(x)-2*sin(x))/(13*(2*cos(x)+3*sin(x)));
end;
begin
writeln(‘vvod’,a,b,n)
readln(a,b,n);
h:=(b-a)/(2*n);
c:=-1;
x:=a;
for i:=1 to 2*n-1 do
begin
x:=x+h;
k:=3+c;
s:=s+k*y(x);
c:=-c;
end;
s:=s+y(a)+y(b);
s:=s*(h/3);
z:=p(b)-p(a);
writeln(‘vivod’,z);
end.
Задание 3.
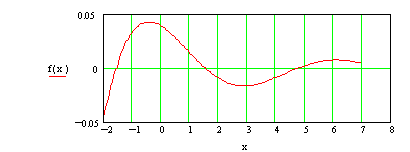
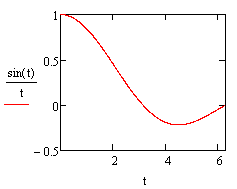
Построить график функции.
Y=1/sqr(3sin(x)+2cos(x)).
Программа.
Program grafik;
uses Graph;
var x0,y0:Word;
сrdr,crm:integer;
x,y:real;
i,j:word;
begin
СrDr:=Detect;
InitGraph(GrDr,Grm,’C:\paskal\BGI’);
if GraphResult <> grok then
begin writeln(‘error graf’);Halt end;
x0:=40;
y0:=GetMaxy;
setbkcolor(1);
y0:=GetMaxy;
setbkcolor(1);
setcolor(15);
Line (x0,0,x0,y0);
Line (x0,y0,getmaxx,y0);
MoveTo(x0,y0);
for i:=1 to getymaxx-40 do
begin
x:=1/(3*sin(x)+2*cos(x)*(3*sin(x)+2*cos(x)));
LineTo(x0+i,y0-round(y*40));
setcolor(15);
Line (x0,0,x0,y0);
Line (x0,y0,getmaxx,y0);
MoveTo(x0,y0);
for i:=1 to getymaxx-40 do
begin
x:=1/(3*sin(x)+2*cos(x)*(3*sin(x)+2*cos(x)));
z:=78*sin(x)+44*cos(x)* 78*sin(x)+2*cos(x);
e:=cos(x)
LineTo(x0+i,y0-round(y*40));
end;
readln;
CloseGraph;
end.
Похожие работы
... корни находятся на расстоянии b: . Тогда , откуда Знак перед корнем выбирают с таким расчетом, чтобы получить наибольшее значение знаменателя. Еще один метод, который применяют для поиска корней полиномов, – метод сопровождающей матрицы (companion matrix). Можно доказать, что матрица , называемая сопровождающей матрицей для полинома , имеет собственные значения равные корням полинома ...
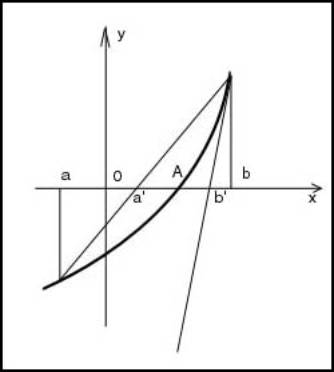
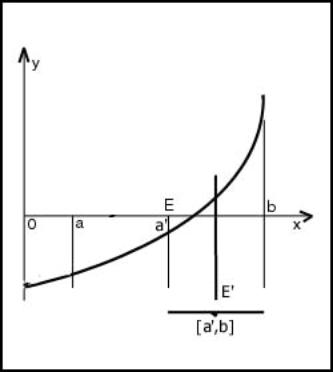
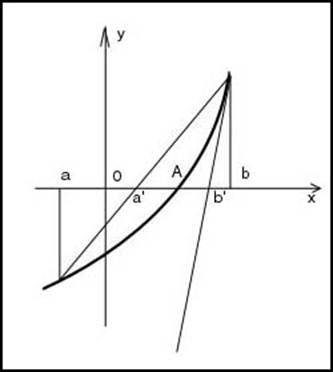
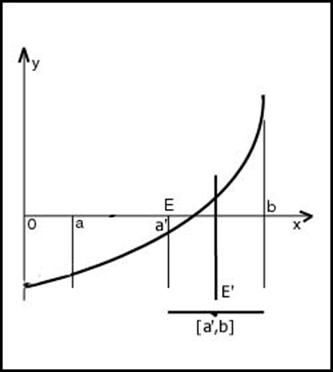
... не будет. Эти контраргументы стали основанием для отклонения метода итераций при выборе алгоритмизируемого метода. 2.2.3. Метод половинного деления (метод бисекции) рис.2 Метод половинного деления (известный еще и как «метод деления отрезка пополам») также является рекурсивным, т.е. предусматривает повторение с учетом полученных результатов. ...
... 4. АНАЛИЗ РЕЗУЛЬТАТОВ В результате выполнения задания на курсовую работу была создана программа VI Function 2.0 , находящая корни алгебраического многочлена вида (1) с указываемой точностью посредством следующих методов: · метод деления отрезка пополам; · метод хорд и касательных (комбинированный) Также при составлении программы была учтена возможность наличия у многочлена кратных ...
... Полученные в MathCAD и с помощью программы по заданию результаты совпадают 10. Основные выводы 1. Обоснованы и выбраны численные методы: - интегрирования по методу Симпсона - отыскания корня уравнения (метод половинного деления) 2. Разработаны, протестированы модули, реализующие следующие методы: - численное интегрирование по методу Симпсона с оценкой погрешности

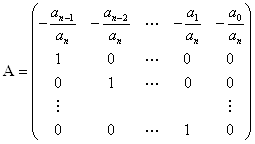


0 комментариев