Приближенное вычисление значений определенного интеграла

Федеральное агентство по образованию РФ

Тульский государственный университет

Кафедра АОТ и ОС

КУРСОВАЯ РАБОТА

по курсу информатика

"ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА"

Тула, 2007

Содержание

Введение

Метод средних прямоугольников

Метод трапеций

Метод Ньютона-Котеса

Метод Чебышева

Блок-схема основной программы

Блок-схема процедуры: метод трапеций

Блок-схема процедуры: метод Ньютона-Котеса

Блок-схема процедуры: метод Чебышева

Текст программы

Список используемой литературы

Введение

На практике редко удается вычислить точно определенный интеграл. Например, в элементарных функциях не вычисляется функция Лапласа

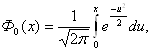
широко используемая в теории вероятностей для вычисления вероятностей, связанных с нормально распределенными случайными величинами.

Задача численного интегрирования состоит в нахождении приближенного значения интеграла:

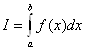 (1)

от непрерывной на отрезке [a, b] функции .

Численные методы интегрирования применяются в случаях, когда не удается найти аналитическое выражение первообразной для функции  либо если функция  задана таблично. Формулы численного интегрирования называются квадратурными формулами.

Пример: Приближенное неравенство

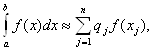(2)

где q_j – некоторые числа, x_j – некоторые точки отрезка [a, b], называется квадратурной формулой, определяемой весами q_j и узлами x_j.

Говорят, что квадратурная формула точна для многочленов степени m, если при замене  на произвольный алгебраический многочлен степени m приближенное равенство (2) становится точным.

Рассмотрим некоторые широко используемые примеры приближенного вычисления определенных интегралов, квадратурные формулы.

Метод средних прямоугольников

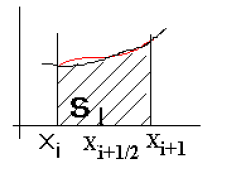
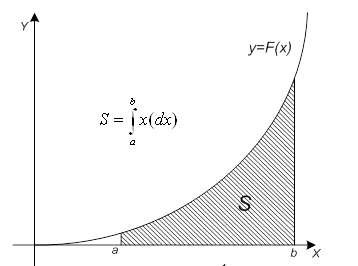
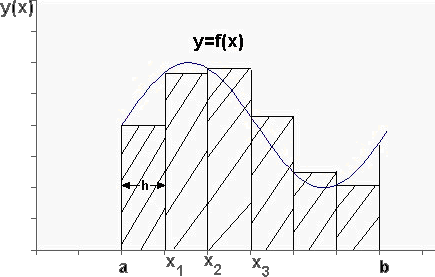
Вычисление определенного интеграла геометрически означает вычисление площади фигуры, ограниченной кривой , прямыми х=а и х=b и осью абсцисс. Приближенно эта площадь равна сумме площадей прямоугольников.

Обозначим  , где

n – количество шагов.

Формула левых прямоугольников:

Формула правых прямоугольников:

Более точной является формула средних прямоугольников:

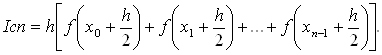
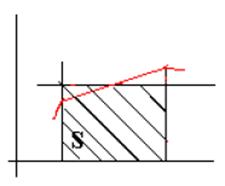
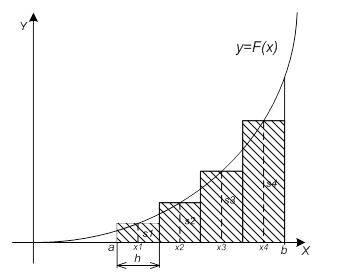
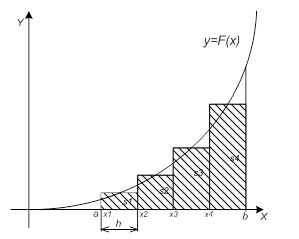
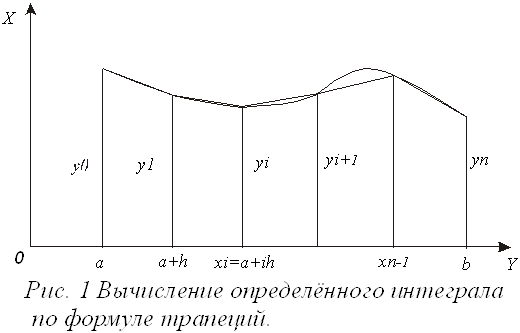
Метод трапеций

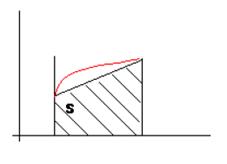
Площадь под кривой заменяется суммой площадей трапеций:

или

Нетрудно убедиться, что

Поскольку точность вычислений по приведенным формулам зависит от числа разбиений n исходного отрезка [a; b], то вычислительный процесс целесообразно строить итерационным методом, увеличивая n до тех пор, пока не будет выполнено условие

<

где  – значения интеграла на  шаге, а  – точность вычислений.

Метод Ньютона-Котеса

Заменим подынтегральную функцию f(x) интерполяционным многочленом Лагранжа:

 .

Тогда

;

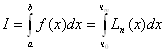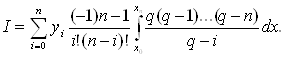 (1)

Так как dx=hdq, то

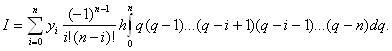
Так как , то

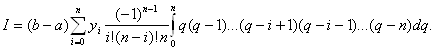
Окончательно получаем формулу Ньютона-Котеса:

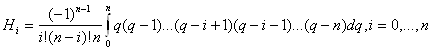(2)

Величины H_i называют коэффициентами Ньютона-Котеса. Они не зависят от f(x). Их можно вычислить заранее для различного числа узлов n (таблица 1).

Формула Ньютона-Котеса с n узлами точна для полиномов степени не выше n. Для получения большей точности не рекомендуется использовать формулы с большим числом узлов, а лучше разбивать отрезок на подотрезки, к каждому из которых применяется формула с одним и тем же небольшим числом узлов.

Таблица 1. Значения коэффициентов Ньютона-Котеса

H	N
	1	2	3	4
H0	1/2	1/6	1/8	7/90
H1	1/2	2/3	3/8	16/45
H2	-	1/6	3/8	2/15
H3	-	-	1/8	16/45
H4	-	-	-	7/90

Интересно отметить, что из формулы (2) следуют как частные случаи: формула трапеций при n=1

;

формула Симпсона при n=2

;

правило трех восьмых при n=3

.

Формулу (2) при n>6 не применяют, так как коэффициенты Ньютона-Котеса становятся слишком большими и вычислительная погрешность резко возрастает.

Метод Чебышева

П.Л. Чебышев предложил формулу:

,

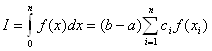в которой коэффициенты c_i фиксированы, а х_i подлежат определению.

Пользуясь алгебраическими свойствами симметричных многочленов, опустив преобразования, ограничимся готовыми результатами. В таблице 2 приведены значения узлов квадратурной формулы Чебышева для некоторых значений n.

Таблица 2. Значения узлов квадратурной формулы Чебышева

Число интервалов n	Номер узла i	Значение узла Xi
1	1 2	0,211325 0,788675
2	1 2 3	0,146447 0,500000 0,853553
3	1 2 3 4	0,102673 0,406204 0,593796 0,897327
4	1 2 3 4 5	0,083751 0,312730 0,500000 0,687270 0,916249
5	1 2 3 4 5 6	0,066877 0,288740 0,366682 0,633318 0,712260 0,933123

Для любых пределов интегрирования имеем:

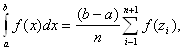 где ,

Значения x_i берутся из таблицы при выбранном значении n. Для повышения точности можно не только увеличивать количество узлов, но и разбивать отрезок [a, b] на подотрезки, к каждому из которых применяется соответствующая формула. Не рекомендуется применять формулы с большим количеством узлов (n>=8).Доказано, что для n=8 построить квадратурную формулу Чебышева невозможно.

 

Блок-схема основной программы

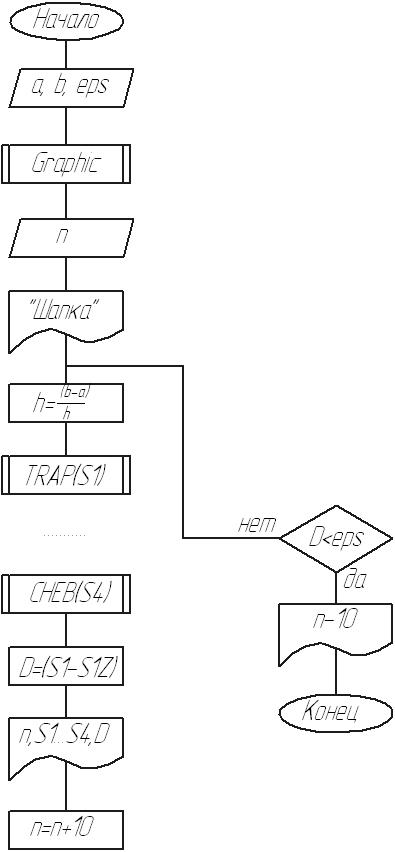
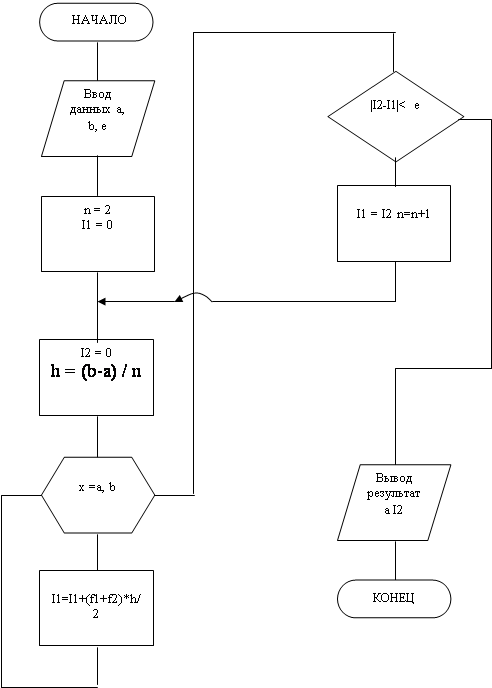
Блок-схема процедуры: метод трапеций

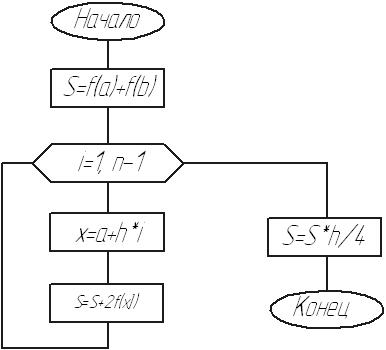
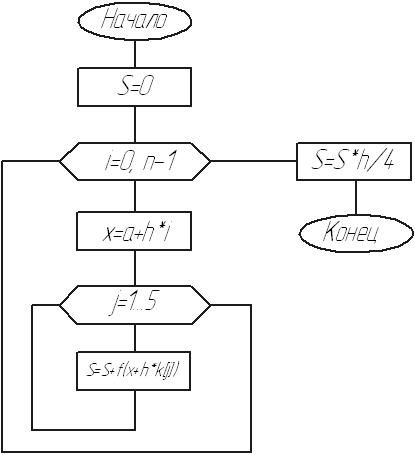
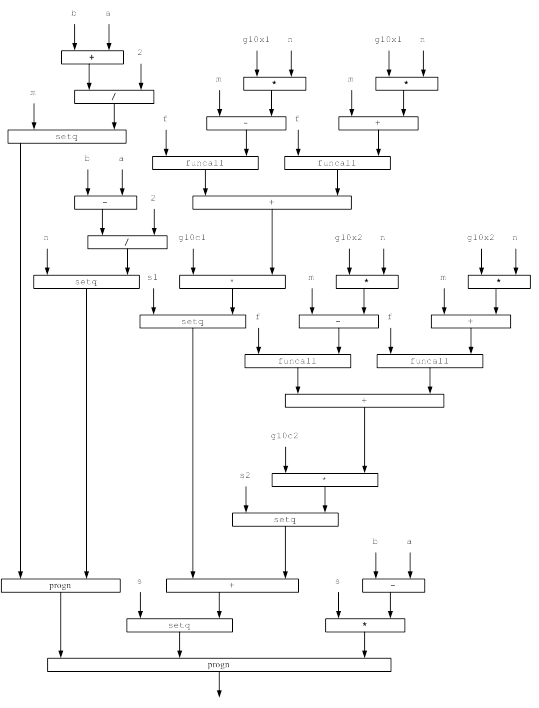
Блок-схема процедуры: метод Ньютона-Котеса

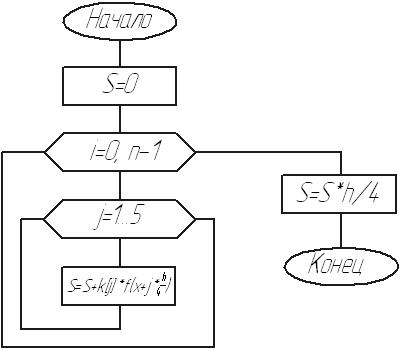
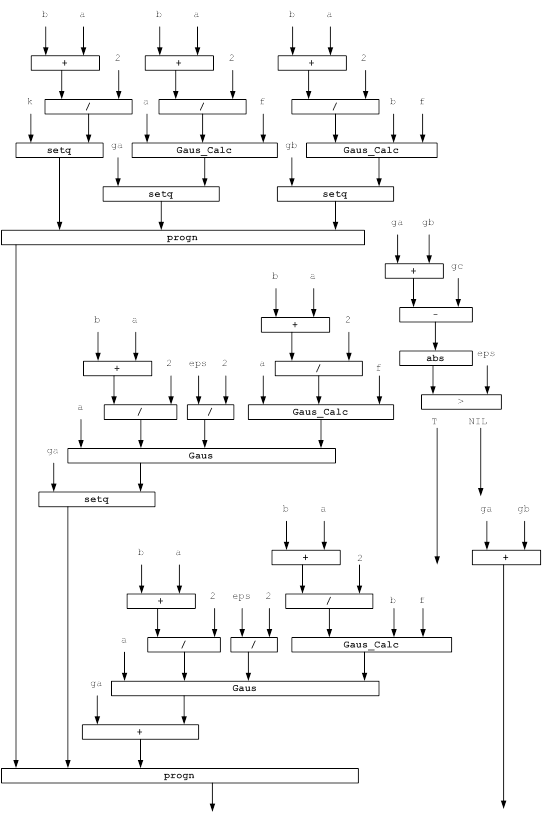
Блок-схема процедуры: метод Чебышева

Текст программы

program Curs;

uses crt, graph;

var i, n:integer;

t:byte;

a, b, eps, h:real;

x, sum1, sum2, seps, m0, m1, m2, m3, m4:real;

lf:text;

st:string;

function f (x:real):real;

begin

f:=19.44*exp (0.224*x);

end;

procedure gr (xn, xk:real);

var x, y, mx, my, dx, dy,

ymin, ymax, xh:real;

xb, yb, xm, ym, xl, yv, xp, yn, bord1, bord2, bord3, bord4, xt, yt, xt1, yt1, dxp, dyp, nd, nr, i, kx, ky, k:integer;

st:string;

begin

k:=100;

xh:=(xk-xn)/100;

ymax:=f(xn);

dx:=(xk-xn)/100;

for i:=1 to 100 do

begin x:=xn+dx*i;

y:=f(x);

if y>ymax then ymax:=y;

end;

ymin:=0;

ymax:=round(ymax);

nd:=detect;

initgraph (nd, nr, 'c:\tp7\bgi');

bord1:=60; kx:=6;

bord2:=30; ky:=8;

bord3:=30;

bord4:=80;

xb:=0; yb:=0; xm:=getmaxx; ym:=getmaxy;

xl:=xb+bord1;

xp:=xm-bord2;

yv:=yb+bord3;

yn:=ym-bord4;

dxp:=(xp-xl) div kx;

dyp:=(yn-yv) div ky;

dx:=(xk-xn)/kx;

dy:=(ymax-ymin)/ky;

xl:=xp-dxp*kx;

yn:=yv+dyp*ky;

mx:=(xp-xl)/(xk-xn);

my:=(yn-yv)/(ymax-ymin);

setfillstyle (1,15);

bar (xb, yb, xm, ym);

setcolor(0);

setlinestyle (0,0,1);

bar (xl, yv, xp, yn);

rectangle (xl, yv, xp, yn);

settextjustify (0,2);

settextstyle (2,1,4);

setcolor(9);

for i:=0 to kx do begin

xt:=xl+dxp*i;

str (xn+dx*i:6:3, st);

line (xt, yn‑3, xt, yn+3);

outtextxy (xt+4, yn+8, st);

end;

settextstyle (0,0,1);

for i:=0 to ky do begin

yt:=yv+dyp*i;

str (ymax-dy*i:6:3, st);

line (xl‑3, yt, xl+3, yt);

outtextxy (xl‑56, yt‑4, st);

end;

outtextxy (xl+100, bord3 div 2,'y=19.44*exp (0.224*x)');

setcolor(12);

if xn*xk<0 then begin

xt:=xl-trunc (xn*mx);

line (xt, yv, xt, yn);

end;

if ymax*ymin<0 then begin

yt:=yv+trunc (ymax*my);

line (xl, yt, xp, yt);

end;

xh:=(xk-xn)/5;

for i:=0 to 5 do begin

setcolor(3);

x:=xn+xh*i;

y:=f(x);

xt:=xl+trunc((x-xn)*mx);

yt:=yv+trunc((ymax-y)*my);

circle (xt, yt, 3);

if i>0 then

line (xt, yt, xt1, yt1);

setcolor(5);

rectangle (xt1, yt1, xt, yn);

xt1:=xt;

yt1:=yt;

end;

repeat until keypressed;

closegraph;

end;

function pr:real;

var s, x:real;

begin

s:=0;

x:=a;

for i:=1 to n do

begin

s:=s+abs (f(x))*h;

x:=x+h;

end;

pr:=s;

end;

function tr:real;

var s, x:real;

begin

s:=0;

x:=a;

for i:=1 to n do

begin

s:=s+(f(x)+f (x+h))/2*h;

x:=x+h;

end;

tr:=s;

end;

function ch:real;

var s, dp, kf, a1, b1:real;

begin

s:=0;

kf:=sqrt (1/3);

for i:=2 to n+1 do

begin

a1:=a+h*(i‑2);

b1:=a1+h;

s:=s+((b1‑a1)/2)*(f((a1+b1)/2‑kf*((b1‑a1)/2))+f((a1+b1)/2+kf*((b1‑a1)/2)));

end;

ch:=s;

end;

function si:real;

var s, x, f1, f2:real;

begin

s:=0;

x:=a;

i:=1;

f1:=0;

repeat

f1:=f1+f (a+h*i);

i:=i+2;

until i>=n;

i:=2;

f2:=0;

repeat

f2:=f2+f (a+h*i);

i:=i+2;

until i>=n;

s:=h/3*(f(a)+f (b-h)+(4*f1)+(2*f2));

si:=s;

end;

begin

assign (lf, 'otchet.txt');

rewrite(lf);

clrscr;

write ('Введите значение левого предела интегрирования: '); readln(a);

write ('Введите значение правого предела интегрирования: '); readln(b);

write ('Введите значение погрешности: '); readln(eps);

write ('Введите начальное значение количества разбиений: '); readln(n);

writeln;

gr (a, b);

write ('Ждите, идет обработка данных ');

m0:=0;

writeln (lf, ' КУРСОВАЯ РАБОТА');

writeln (lf, ' ПО КУРСУ ИНФОРМАТИКА');

writeln (lf, ' «ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ');

writeln (lf, ' ОПРЕДЕЛЕННОГО ИНТЕГРАЛА» ');

writeln (lf, ' Выполнил: студент гр. ');

writeln (lf, ' Вариант 22 y=19.44*exp (0.224*x)');

writeln (lf, ' Xn=', a:5:3,' Xk=', b:5:3,' Eps=', eps:5:3);

writeln(lf);

writeln (lf, ' РЕЗУЛЬТАТЫ ВЫЧИСЛЕНИЙ');

repeat

h:=abs (b-a)/n;

m1:=pr;

m2:=tr;

m3:=si;

m4:=ch;

seps:=abs (m1‑m0);

writeln (lf, ' │', n:7,' │', m1:11:8,'│', m2:11:8,'│', m3:11:8,'│', m4:11:8,'│', seps:11:8,'│');

m0:=m1;

n:=n+200;

until (seps<=eps);

clrscr;

reset(lf);

while not eof(lf) do

begin

readln (lf, st);

writeln(st);

end;

{write ('Нажмите <Enter> для выхода из программы');

repeat until keypressed;}

close(lf);

end.

Список используемой литературы

1.   Бахвалов Н.С. «Численные методы». М.: Наука, 1987 – 598 с.

2.   Калиткин Н.Н. «Численные методы». М.: Наука, 1988 – 512 с.

3.   Крылов В.И. «Вычислительные методы». М.: Наука, 1977 – 408 с.

4.   Нечаев В.И., Нечаева О.А., Почуева Л.Н. «Численные методы». Тула, 1999.