Проектирование линейных стационарных САУ с микропроцессорными регуляторами

Введение

Цель курсовой работы получить навыки расчета линейных стационарных САУ с микропроцессорными регуляторами.

В первой половине работы применить метод расчета последовательного корректирующего устройства, основанного на использовании логарифмических частотных характеристик, а также исследовать динамику САУ моделированием ее на ПЭВМ в системе ''MATLAB ~ Simulink.

Во второй половине работы на основании полученной передаточной функции корректирующего устройства рассчитывается дискретная передаточная функции регулятора. Далее производится исследование динамики уже дискретной системы.

В связи с использованием в контуре управления Микропроцессорного регулятора, помимо обычных требований по обеспечению устойчивости, точности и качества проектируемой САУ, учитываются требования к шагам квантования сигналов по уровню и по времени. Частоты квантования по уровню и времени выбираются так, что система приближенно может рассматриваться как линейная непрерывная САУ. Это позволяет использовать для расчета закона управления простой и эффективный аппарат логарифмических частотных характеристик. Затем закон управления представляется в дискретной форме для получения переходного процесса уже в дискретной системе.

В качестве критерия правильности расчета можно поставить идентичность переходных процессов в линейной и микропроцессорной системе, выбирая соответствующий период квантования по времени.

1. Неизменяемая часть системы

Проектирование САУ всегда начинается с анализа объекта, формулировки задачи функционирования проектируемой системы, выбора критерия качества системы или задания требований к системе.

Будем считать, что этап анализа объекта, получения уравнений объекта и их линеаризация, выбор исполнительного механизма и датчиков уже решен, Полученные данные будут составлять так называемую неизменяемую часть системы.

Получим, что передаточная функция такой неизменяемой части системы имеет вид

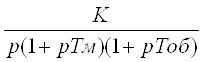
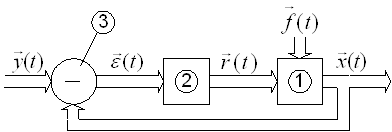
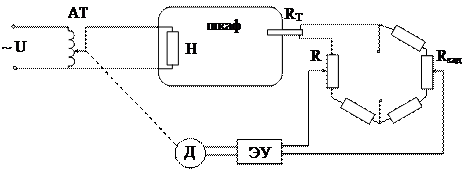
2. Структурная схема САУ с микропроцессорным регулятором

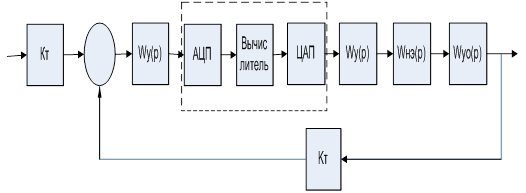
Поскольку микропроцессорный регулятор построен на базе Микро-ЭВМ и может обрабатывать сигналы только дискретной формы" а сигнал на выходе объекта Ux и регулирующий сигнал U_r - непрерывны, то необходимо использовать преобразователи сигналов. АЦП - аналогово-цифровой преобразователь осуществляет кодирование непрерывного сигнала Ux дискретным сигналом 1х- ЦАП -цифро-аналоговый преобразователь преобразовывает дискретный сигнал регулирования 1_г в непрерывный U_r. В процессе аналого-цифрового преобразования осуществляется квантование сигнала по времени и по уровню и это оказывает серьёзное влияние на динамические процессы в САР.

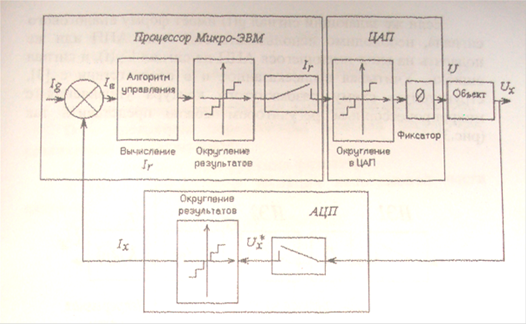
Рис. 2

На рис. 2 представлена в общем виде структурная схема САР с микропроцессорным регулятором и форма используемых в такой системе сигналов [1]. Непрерывный сигнал Ux(t) с выхода объекта поступает сначала в АЦП, где производится квантование сигнала по времени с постоянным шагом То в моменты t - 0, То, 2То, ... , кТо.

В результате этого будет получен дискретный сигнал u*_x(k)<. д^^ производится квантование сигнала по уровню путём округления Ух Д° ближайшего стандартного значения Полученный при этом сигнал 1_г представляет собой последовательность цифровых двоичных кодов, которые в дискретные моменты времени передаются в процессор и Микро-ЭВМ вырабатывает дискретный сигнал ошибки на основе которого в каждый тактовый момент времени 0' Т 2Т₀,.... кТо вычисляется в соответствии с выбранным законом регулирования регулирующий сигнал Щ), Тх в процессе вычисления регулирующего воздействия могут использоваться операции умножения или другие арифметические операции, приводящие к переполнению разрядной сетки Микро-ЭВМ, полученный сигнал вновь подвергается округлению, а затем в дискретные моменты времени выдаётся в ЦАП. Если число разрядов микропроцессора и ЦАП не совпадают, в ЦАП вновь производится округление. На выходе ЦАП имеется экстраполятор, который превращает цифровой код в аналоговый кусочно линейный сигнал. В Микро-ЭВМ чаще всего используются экстраполяторы нулевого порядка, которые носят название фиксаторов и превращают цифровой код в аналоговый ступенчатый сигнал. Этот сигнал воздействует на исполнительный механизм, осуществляя процесс регулирования. В приведённой на рис.2 схеме САР задающей сигнал Ig имеет цифровую форму.

Такой сигнал может быть получен от специального цифрового датчика или другой Микро-ЭВМ.

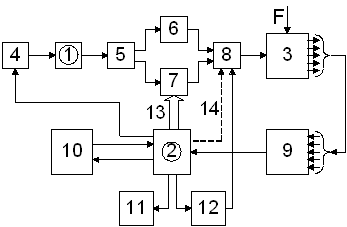
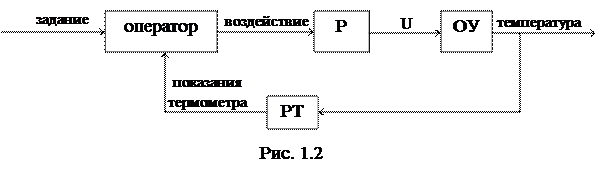
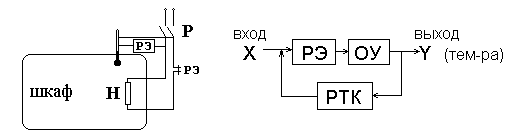
Функциональная схема линейной САУ

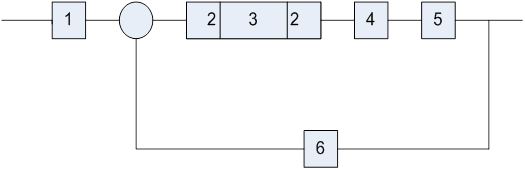
1 – датчик входного сигнала

2 - согласующий усилитель

3 - последовательное КУ

4 – исполнительный элемент (двигатель)

5 - управляемый объект

6 – датчик выходного сигнала (температуры)

g – заданное значение температуры

Ux – температура на выходе системы

E – ошибка

U – управляющее воздействие

Функциональная схема МП САУ

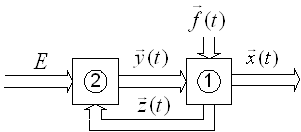
Структурная схема линейной САУ

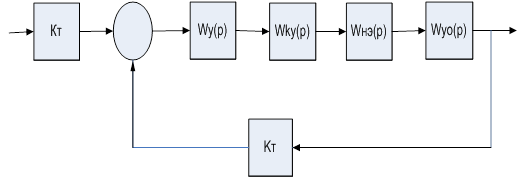
Структурная схема МП САУ

В рассматриваемой системе регулирования температуры технологического процесса учтем исходные данные, характеризующие неизменяемую часть системы.

Кроме этого к системе предъявляются следующие требования:

·          максимальное перерегулирование σ = 30 %;

·          максимальное время регулирования: t = 55 сек;

·          запас устойчивости по фазе Δφ (Град) должен лежать в пределах 35° - 65° в соответствии с диапазоном изменения σ % от 40% до 20% в исходных данных

·          Коэффициенты ошибок Do= 0 D = 0,058

В нашем случае передаточная функция неизменной части системы имеет вид:

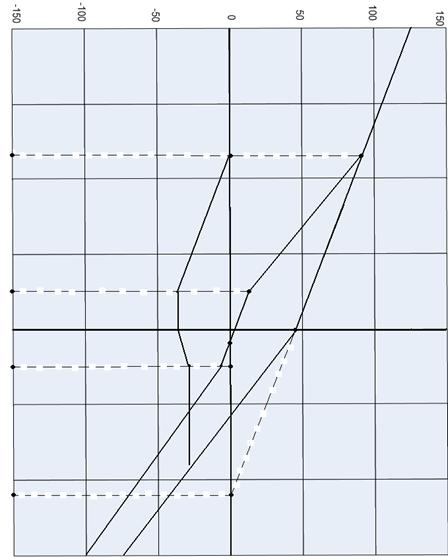
Для построения ЛЧХ на оси частот выбираем точку  1/с и проводим асимптоту с наклоном -20 дБ/дек

Построение необходимо проводить в соответствии с выражением ЛЧХ

Фазочастотную характеристику строим по формуле:

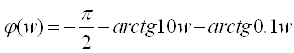
	0.1	0.2	0.5	0.8	1
	-135,57	-154,3	171,56	176,5	180

В рассматриваемой РГР σ = 30 % и t = 55 сек.

Из таблицы находим B = 11,3; Wср=0,2 1/с

Найдем

0.2

L1=15 дБ

Синтез линейной САУ

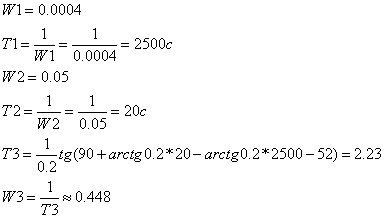
Определим передаточную функцию желаемого регулятора

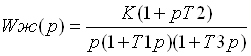
Определим передаточную функцию корректирующего устройства

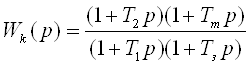
Передаточная функция замкнутой системы имеет вид:

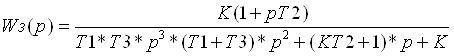
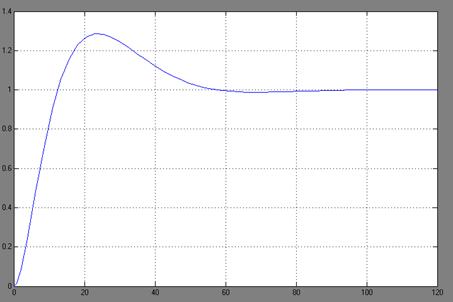
Получим переходный процесс в системе моделированием её на ЭВМ.

Переходный процесс в линейной САУ

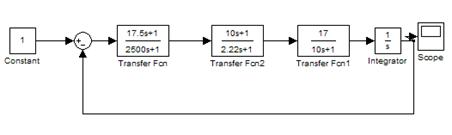
Определение дискретной передаточной функции корректирующего звена.

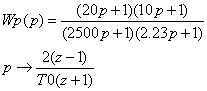
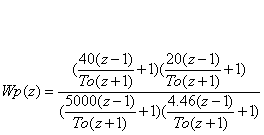
При T0 = 0.35

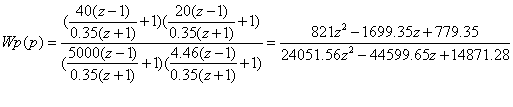
При T0 = 0.25

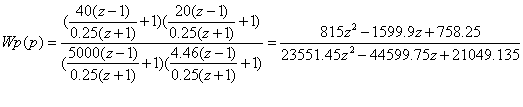
При T0 = 0.1

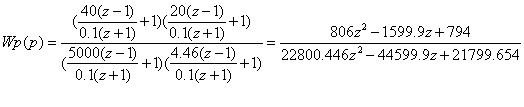
Для моделирования САУ в пакете "ДИСПАС" соответствующее уравнение имеет вид:

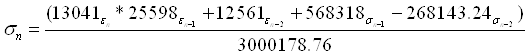
Переходный процесс в дискретной САУ при шаге квантования

Т=0.35

Схема моделирования при Т0=0.35

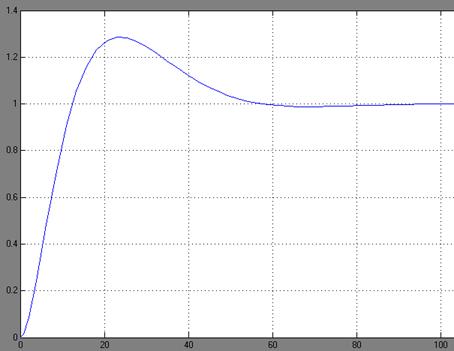
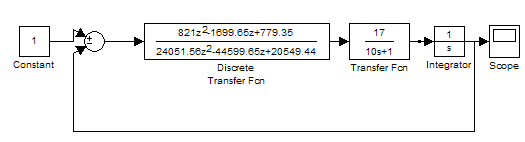
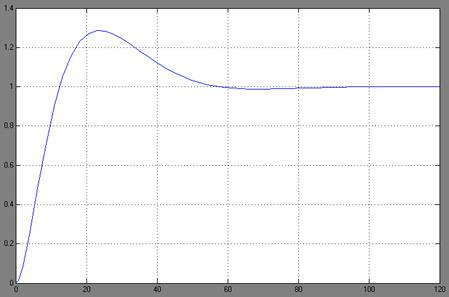
Переходный процесс в дискретной САУ при шаге квантования

Т=0.25

Схема моделирования при Т0=0.25

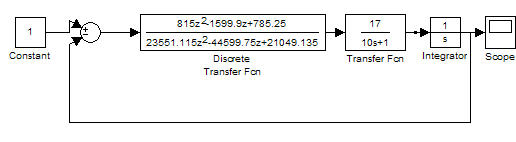
Переходный процесс в дискретной САУ при шаге квантования

Т=0.1

Схема моделирования при Т0=0.1

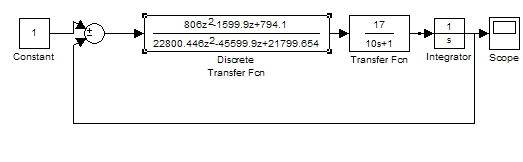
Выводы

В результате проделанной работы было выяснено, что независимо от того, каким способом анализировать результаты разработки САУ с микропроцессорным регулятором, в результате анализа необходимо получить график переходного процесса.

Вывели дискретную передаточную функцию регулятора, для того чтобы исследовать динамику САУ с микропроцессорным регулятором, так же выбрали шаг квантования Т0. Для исследования системы и решения задачи можно использовать пакет "MATLAB" и др. По полученному графику убедились в устойчивости системы. Убедились, что процессы в линейной и дискретной САУ идентичны, следовательно расчеты произведены верно и задачу можно считать выполненой.