Курсовая работа по информатике
на тему:
«Задача о Ханойских башнях»
Содержание
Введение
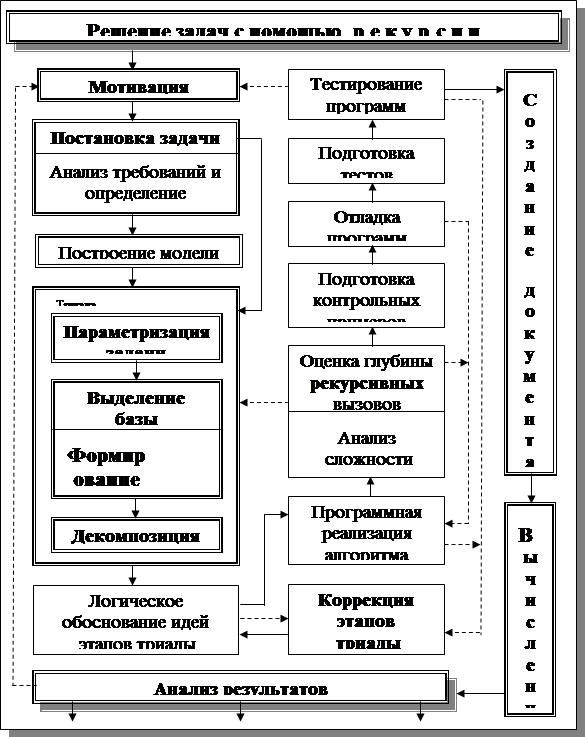
1. Построение модели
2. Разработка алгоритма
2.1 Пошаговый алгоритм
2.2 Структограмма
3. Проверка правильности алгоритма
4. Анализ алгоритма и его сложности
5. Реализация алгоритма
Введение
Задача о Ханойских башнях. На одном из алмазных шпилей надето 64 круглых золотых диска. Диски имеют разные радиусы и расположены на шпиле в порядке убывания радиусов от основания к вершине. Требуется перенести диски с первого на второй, используя по необходимости и третий шпиль. При этом неукоснительно должны соблюдаться следующие правила:
за один раз можно перемещать только один диск;
больший диск нельзя располагать на меньшем диске;
снятый диск необходимо надеть на какой-либо шпиль перед тем, как будет снят следующий диск.
Трудолюбивые буддийские монахи день и ночь переносят диски со шпиля на шпиль. Легенда утверждает, что когда монахи закончат свою работу, наступит конец света. Можно было бы подсчитать, что для решения задачи с 64 дисками потребуется 264-1 перемещений (около 1020). Поэтому, что касается конца света, то он произойдет по истечении пяти миллиардов веков, если считать, что один диск перемещается за одну секунду. Впрочем и задачу, и легенду для неё придумал в 1883 году математик Э.Люка. Это дает нам право отложить заботы о конце света в сторону и перейти к решению следующей задачи.
Постановка задачи.
Имеется три колышка a, b, c и n дисков разного размера, переномерованных от 1 до n в порядке возрастания их размеров. Сначала все диски надеты на колышек a (рисунок 1.1),
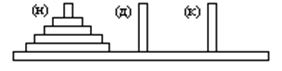
Рисунок 1.1
требуется перенести все диски с колышка a на колышек c (рисунок 1.2),
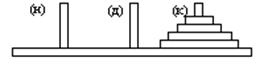
Рисунок 1.2
соблюдая при этом следующие условия:
диски можно переносить только по одному;
больший нельзя ставить на меньший (рисунок 1.3).
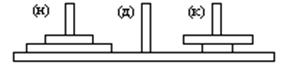
Рисунок 1.3
Написать программу, которая печатает последовательность действий (в виде «перенести диск с q на r», где q и r – это a, b или c, решающую указанную задачу для n дисков, n – заданное натуральное число).
Целью данной курсовой работы является изучение рекурсивного алгоритма решения задачи о Ханойских башнях, разработка программы, печатающей последовательность действий.
1. Построение модели
Математической моделью данной задачи является рекуррентное соотношение.
Рекуррентное соотношение – это соотношение, которое выражает значение функции с помощью других значений, вычисленных для меньших аргументов. Исходя из данного определения, следует, что для каждой рекуррентной функции нужно задавать хотя бы одно значение.
2. Разработка алгоритма
Для разработки алгоритма решения данной задачи используется рекурсивный метод.
При построении алгоритма используется подход «разделяй и властвуй». Идея заключается в следующем:
задача разбивается на несколько подзадач меньшего размера;
решаются эти подзадачи;
решения подзадач комбинируются, и получается решение исходной задачи.
Как правило, задачи решаются непосредственно, либо с помощью рекурсивного вызова.
Алгоритм называется рекурсивным, если при решении некоторой задачи он вызывает сам себя для решения подзадачи.
Для того, чтобы переложить всю пирамиду из дисков, надо сначала переложить все, что выше самого большого диска, с первого на вспомогательный колышек, потом переложить этот самый большой диск с первого на третий колышек, а потом переложить оставшуюся пирамиду со второго на третий колышек, пользуясь первым колышком как вспомогательным.
2.1 Пошаговый алгоритм (с рекурсией)
Входные данные: количество дисков, находящихся на колышке a;
Выходные данные: последовательность действий;
Шаг0:{определение типа переменных};
Шаг1:{описание процедуры Pernesti, которая выводит последовательность действий};
Шаг1.1:{переместить (n-1) дисков с колышка a на колышек b};
Шаг1.2:{переместить n-ый диск с a на c};
Шаг1.3:{переместить (n-1) диск с b на c};
(шаги 1.2-1.3 выполняются рекурсивно);
Шаг2:{основная программа};
Шаг2.1:{ввод количества дисков};
Шаг2.2:{вызов процедуры Perenesti}.
2.2 Структограмма

3. Проверка правильности алгоритма
Правильность алгоритма проверим при n=3 и n=4.
n=3
переместить диск со стержня a на стержень c
переместить диск со стержня a на стержень b
переместить диск со стержня c на стержень b
переместить диск со стержня a на стержень c
переместить диск со стержня b на стержень a
переместить диск со стержня b на стержень c
переместить диск со стержня a на стержень c
n=4
переместить диск со стержня a на стержень b
переместить диск со стержня a на стержень c
переместить диск со стержня b на стержень c
переместить диск со стержня a на стержень b
переместить диск со стержня c на стержень a
переместить диск со стержня c на стержень b
переместить диск со стержня a на стержень b
переместить диск со стержня a на стержень c
переместить диск со стержня b на стержень c
переместить диск со стержня b на стержень a
переместить диск со стержня c на стержень a
переместить диск со стержня b на стержень c
переместить диск со стержня a на стержень b
переместить диск со стержня a на стержень c
переместить диск со стержня b на стержень c
4. Анализ алгоритма и его сложности
Алгоритм решения задачи о Ханойских башнях является конечным, так как все используемые циклы выполняются конечное число раз.
Сложность – количественная характеристика алгоритма, которая говорит о том, сколько времени он работает (временная сложность), либо о том, какой объем памяти он занимает (емкостная сложность). На практике сложность рассматривают как временную сложность.
Из определения сложности следует, что она зависит от размерности входных данных или, как говорят, от длины входа. В задаче о Ханойских башнях входными данными является число дисков.
Рассчитаем порядок временной сложности в соответствии с пошаговым алгоритмом.
Временная сложность процедуры Perenesti будет зависеть от количества переносов, которое равно 2n-1, значит О(2n-1).
5. Реализация алгоритма
Program kyrsovaya;
uses crt;(подключение модуля очистки экрана)
var(описание переменных)
n: integer;(целый тип данных)
a,b,c: char;(описание символьных типов данных)
procedure Perenesti(n: integer;a,b,c: char);
begin(начало процедуры)
if n>0 then(если n>0 значит)
begin
Perenesti(n-1,a,c,b);
writeln ('Peremestit" disk so sterzhnya ',a,' na sterzhen" ',b);(ввели)
Perenesti(n-1,c,b,a);
end;
end;
begin
clrscr;(очистка экрана)
writeln ('Vvedite natural"noe chislo n');
read (n);(ввод числовых данных)
a:='a'; b:='b'; c:='c';присвоение по членных переменных (то ,что до этого ввели)
Perenesti (n,a,c,b);
readln;(процедура чтения)
end.
Похожие работы
... тогда ; · n = 5k + 2, тогда ; · n = 5k + 3, тогда ; · n = 5k + 4, тогда . Из пунктов 1 и 2 следует: для n ≥ 5 . Ответ: при всех n ≥ 0 и k, r Z+. Задача 9. Иногда возможно использование «обратной индукции», т.е. доказательства от n к n−1, а не наоборот. К примеру, рассмотрим утверждение P(n): ≤ , если x1,x2,…,xn ≥ ...
... ) F1, F2, … Fk друг друга: F1 вызывает F2, F2 вызывает F3, …, Fkвызывает F1 (k>1). 5. Рекурсивные обращения (рекурсивные вызовы) Прямая или косвенная рекурсия при рекурсивных вычислениях 6. Рекуррентное соотношение (рекуррентная формула) Формула вида an+p=F(an, an+1,…, an+p-1) (p³1), позволяющая вычислять любой член бесконечной последовательности a1, ...
... то получим из них, путём почленного вычитания: un + 2 - un + 1 = un + 1 - un, или un + 2= 2un + 1 - un (5) - уравнение вида (2). Здесь k = 2, a1 = 2, a2 = -1. Следовательно, арифметическая прогрессия является возвратной последовательностью второго порядка. Пример 3. Рассмотрим старинную задачу Фибоначчи о числе кроликов. В ней требуется определить число пар ...
... к указанной выше категории, поскольку в системе задана основная структура знаний, которая корректируется последовательно по отдельным данным. Ярким примером применения этого метода приобретения знаний могут также служить системы распознавания образов (обсуждавшиеся ранее в другом докладе). В них ясно просматривается основной принцип этого метода - в ходе обучения нейронная сеть автоматически по ...
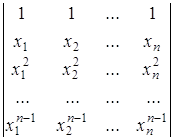
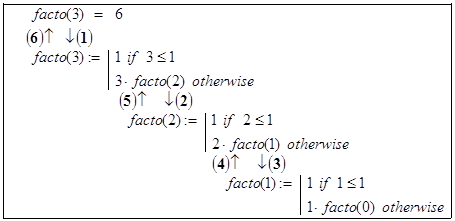
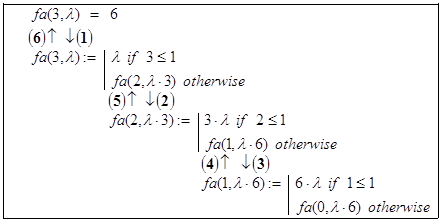

0 комментариев