Предмет:
"Теория автоматического управления"
Тема:
"Расчет переходных процессов в дискретных системах управления"
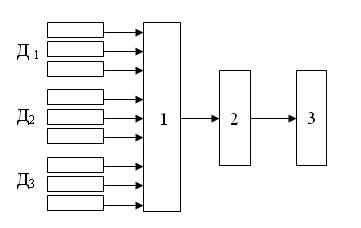
Рассмотрим схему дискретной системы автоматического управления, приведенную на рис. 1.
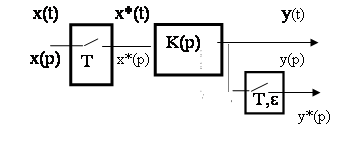
Рис. 1
Для выхода системы можно записать следующие соотношения между входным и выходным сигналом
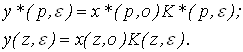 (1)
(1)
Выражение для выходной величины во временной форме имеет вид
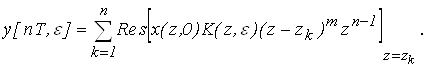 (2)
(2)
Переходную функцию определим из соотношений
 (3)
(3)
Получили выражение для расчета переходной функции дискретной системы.
Определим функцию веса дискретной системы. Дискретное изображение единичного импульса x(t) = d(t) равно x(z) = 1.
Весовую функцию определим из соотношений
 (4)
(4)
Получили выражение для расчета функции веса дискретной системы.
Установившееся значение временных характеристик можно определить с помощью теоремы о конечном значении дискретной функции.
Для переходной функции
![]() . (5)
. (5)
Для весовой функции
![]() (6)
(6)
![]()
Откуда
![]() (7)
(7)
Как следует из выражения (7) функция веса в каждый дискретный момент времени может быть определена как разность между текущим и предыдущим значением переходной функции
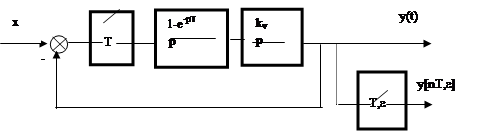
Пример 1. Для заданной системы (рис. 2.) рассчитать переходный процесс, если x(t) = 1 (t). 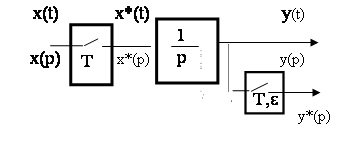
Рис. 2
Решение
Выходной дискретный сигнал равен: ![]()
При этом
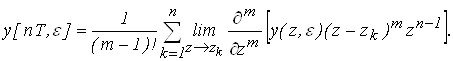
Если x(t) = 1 (t) то 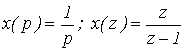 . Для
. Для 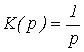
![]()
Подставим x(z) и K (z,e) в выражение для выходного дискретного сигнала

Определим значения полюсов – zk их число – n и кратность – m: z1 = 1; n = 1; m = 2.
Выражение для переходного процесса имеет вид:
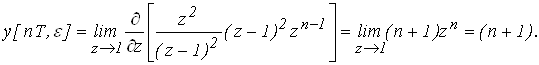
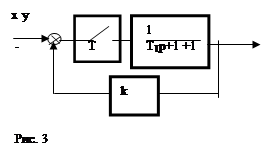
Решение:
Выходной дискретный сигнал равен: ![]()
При этом
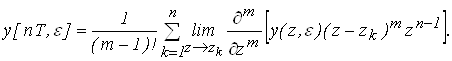 .
.
Если x(t) = 1 (t), то 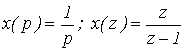 .
.
Для 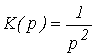
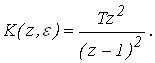
Подставим x(z) и K (z,e) в выражение для выходного дискретного сигнала
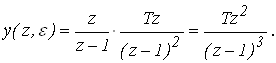
Выражение для переходного процесса имеет вид:
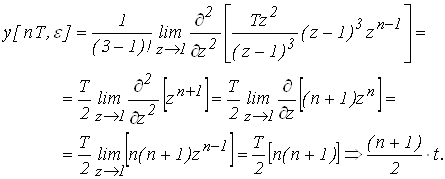
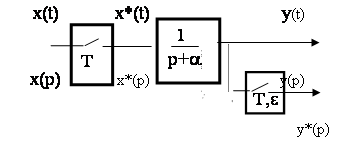
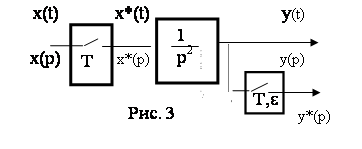
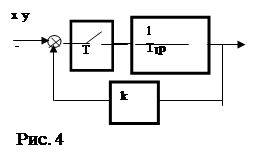
Рис. 4
Решение:
Выходной дискретный сигнал равен: ![]()
При этом
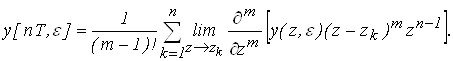
Если x(t) = 1 (t), то 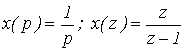 .
.
Если 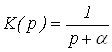 , то
, то 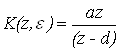 , где
, где![]()
Подставим x(z) и K (z,e) в выражение для выходного дискретного сигнала
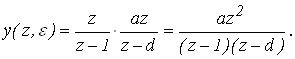
Определим значения полюсов – zk их число – n и кратность – m:
z1 = 1; z2 = d; n = 2; m = 1.
Выражение для переходного процесса имеет вид:
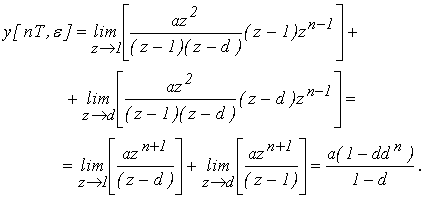
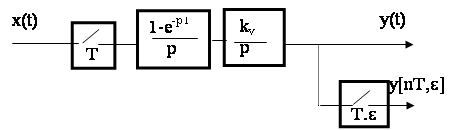
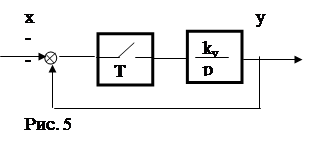
Рис. 5
Решение:
Выходной дискретный сигнал равен: ![]()
При этом
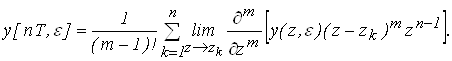
Если x(t) = 1 (t), то 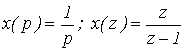 .
.
Передаточная функция соединения равна:
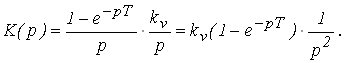
Дискретная передаточная функция соединения равна:

Подставим x(z) и K (z,e) в выражение для выходного дискретного сигнала

Определим значения полюсов – zk их число – n и кратность – m: z1 = 1; n = 1; m = 2.
Выражение для переходного процесса имеет вид:
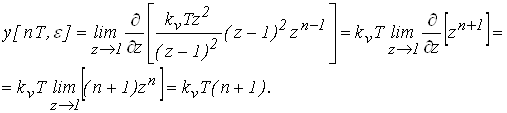
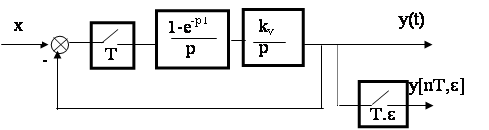
Рис. 6
Решение:
Определим передаточную функцию разомкнутой непрерывной части:
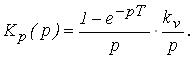
Выполним дискретное преобразование:
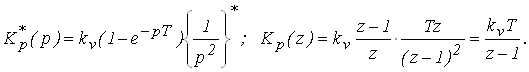
Передаточная функция замкнутой дискретной системы:
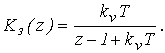
Подставим x(z) и Kз(z,e) в выражение для выходного дискретного сигнала

Определим значения полюсов – zk их число – n и кратность – m:
z1 = 1, z2 = 1 – kv T = A, n = 2, m = 1.
Выражение для переходной функции имеет вид:
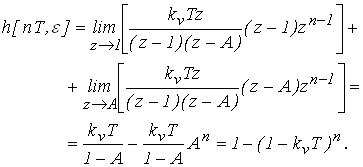
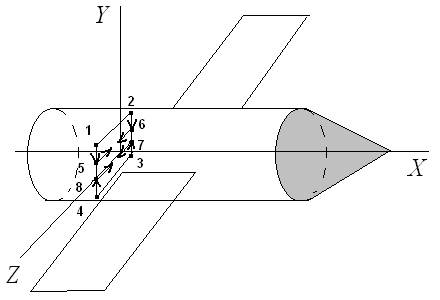
 X Y
X Y
Рис. 7
Решение: Исходную схему можно представить в виде (рис. 8)
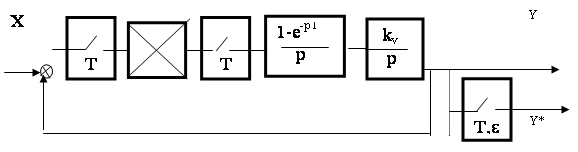
Рис. 8
Определим передаточную функцию разомкнутой непрерывной части
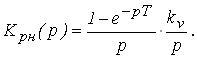
Выполним дискретное преобразование
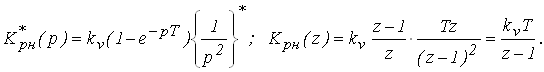
Определим передаточную функцию цифрового автомата, в соответствии с алгоритмом его функционирования
![]()
Определим передаточную функцию разомкнутой дискретной системы:
![]()
Передаточная функция замкнутой дискретной системы:
![]()
где s1, s2 корни характеристического уравнения
![]()
при этом s1+ s2 = 1+a+kv T; s1 s2 = a.
Подставим x(z) и Kз(z,e) в выражение для выходного дискретного сигнала
![]()
Определим значения полюсов – zk их число – n и кратность – m
z1=1, z2=s1, z3=s2, n=2, m=1.
Выражение для переходной функции имеет вид:
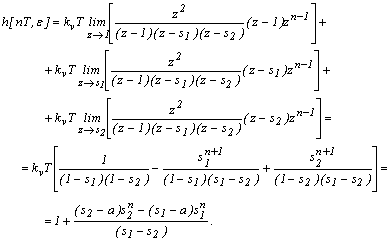
Литература
1. Бронштейн И.Н., Семендяев К.Н. Справочник по математике для инженеров и учащихся вузов. – М.: Наука, 1989
2. Васильев В.И., Ильясов Б.Г. Интеллектуальные системы управления: Теория и практика: Учеб. пособие для вузов. Издательство: Радиотехника, 2009. – 392 с.
3. Голенцев Э., Клименко С.В. Информационное обеспечение систем управления. ФЕНИКС, 2002. – 350 с.
4. Долятовская В.Н., Долятовский В.А. Исследование систем управления, 2004. – 255 с.
Похожие работы
... Определим R(z) , где d=T1 /(T1 +k). 4. Определим величину интеграла J2 с помощью вычетов z1 = d 5. Определим величину интеграла J2 с помощью таблиц 4. Точность дискретных систем управления Точность дискретных САУ оценивается аналогично, как и непрерывных, с учетом некоторых особенностей. Изображение ошибки для дискретной системы равно (5) Установившееся значение ...
... имеют некоторый типовой вид. Сложные (многосвязные) технические объекты в совокупности с узлами (устройствами) управления первого, исполнительного уровня образуют подсистемы оперативного управления, которые представляют собой многосвязные системы автоматического регулирования (МСАР) по типу следящих систем. Задающие воздействия для них формируются на втором, тактическом уровне, а цели управления ...
... .3 +810.3 Срок окупаемости Лет -- 0.242 -- Вывод Из данного расчета и проведенного анализа технико-экономических показателей делаем вывод о целесообразности внедрения «Автоматизированной системы управления компрессорной установкой». Так как в результате годовая экономия затрат от автоматизации системы составляет 3347839.05 рублей. Это достигается за счет экономии в зарплате 785925.5 ...
... , может приводить к большим потерям рабочего тела и раскрутке космического аппарата до недопустимых угловых скоростей. Таким образом разработка алгоритмов контроля и диагностики системы управления ориентацией космического аппарата – является актуальной задачей. В настоящей работе решается задача построения алгоритмов контроля и идентификации отказов командных приборов и исполнительных органов. ...
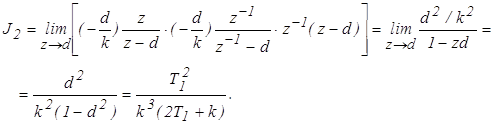

0 комментариев