ОБЩАЯ МЕТОДИКА ВЫПОЛНЕНИЯ ПРОЧНОСТНЫХ РАСЧЕТОВ
При обработки конструкций радиоэлектронной аппаратуры (РЭА), ее составных частей и деталей радиоконструктору необходимо оценить качество принятых конструкторско–технологических решений для выбора оптимального варианта или определения степени соответствия требованиям технического задания (ТЗ).
В процессе эксплуатации на несущие элементы конструкции РЭА, электроэлементы и узлы действуют различные механические силы. На стационарную РЭА действует, в основном, сила тяжести самой конструкции и ее составных частей. Аппаратура, устанавливаемая на подвижных объектах, а также стационарная РЭА во время транспортировки подвергается внешним механическим воздействиям : вибрациям (периодическим колебаниям) или ударам (кратковременно действующим силам).
В ТЗ на конструирование РЭА, как правило, регламентируется следующие параметры механических воздействий :
линейное ускорение а, м/c2, или перегрузка rп, g;
частота вибраций f, Гц, или полоса частот Δf, Гц ;
амплитуда вибраций А, мм ;
продолжительность вибраций Т, ч ;
длительность ударного импульса tи, мс ;
частота ударов в минуту ,υ ;
число ударов N.
Цель расчетов статистической, вибро– и ударопрочности конструкций – определить параметры механических напряжений в конструкциях РЭА в наихудших условиях и сопоставить их с предельно допустимыми.
Если из расчета выяснится, что прочность конструкции РЭА недостаточна, то конструктор принимает решение о вводе добавочных элементов крепления, ребер жесткости, отбортовок и других упрочняющих элементов или о применении для конструкций материалов с лучшими прочностными или демпфирующими свойствами.
Теория сопротивления материалов является основой для оценки статистической прочности конструкций РЭА.
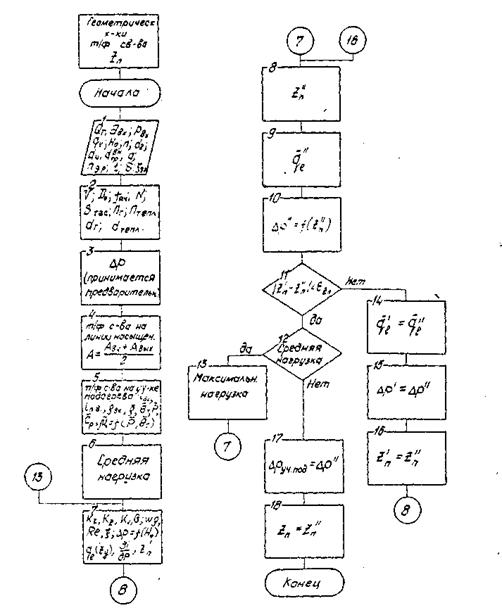
Точная методика для расчета вибрационной и ударной прочности конструкций пока недостаточно разработана, поэтому обще принятым инженерным подходом является приведение динамических задач к статическим. При выполнении оценочных прочностных расчетов студенту следует придерживаться методики, содержащей несколько этапов :
1) выбор расчетных моделей конструкций РЭА и ее элементов ;
2) определение нагрузок, испытываемых элементами конструкций : напряжений, растяжений σр, смятия σсм, среза tср ;
3) расчет допускаемых значений прочности элементов конструкций – напряжений растяжения [σ ]р, смятия [σ ]см, среза [ t ]ср ;
4) сравнение расчетных показателей прочности с допускаемыми.
При оценочном расчете деталей конструкций на прочность принято считать, ели расчетные напряжения σ и t в опастных сечениях не превышают допустимых, то прочность конструкции соответствует требованиям ТЗ. Следовательно, условие обеспечение прочности выражается зависимостями :
σ ≤ [ σ ] или t ≤ [ t ]
В проектных расчетах параметры конструкций а или внешних воздействий φ, обеспечивающие требования прочности, определяются из соотношений :
а = f ([ σ ], [ t ]); Р = φ ([ σ ], [ t ]).
При расчете прочности конструкцию РЭА условно заменяют эквивалентной расчетной схемой, для которой известно аналитическое выражение основных колебаний f0. Основное условие замены состоит в том, чтобы расчетная схема наилучшим способом соответствовала реальной конструкции и имела минимальное число степеней свободы.
Наиболее часто применяются два вида моделей – балочное и пластинчатые.
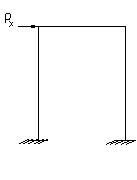
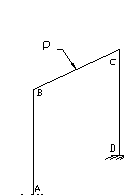
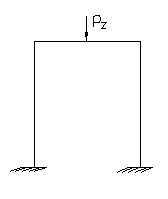
К балочным моделям следует приводить элементы конструкций призматической формы, высота (толщена) которых мала по сравнению с длиной. Концы жестко защемлены, оперты или свободны.
К жесткому замещению приравнивают сварку, пайку и приклеивание, к опоре – винтовое закрепление.
В нижеприведенных формулах приведены виды и схемы балок при различных нагрузках и соответствующие им расчетные соотношения для определения максимального прогиба zmax, м ; максимального изгибающего момента Мизг, Н·м и частоты собственных колебаний f0 Гц.Здесь e – модуль упругости материала, Па ; I – момент инерции, м4 ; l – длина, м ; М и m – масса блоков и балки, кг ; Р – сила, Н.
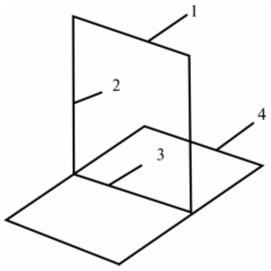
Пластинчатые модели студенту следует использовать для тел призматической формы, высота (толщина) h которых мала по сравнению с размерами основания а, в. Крепление пластин жесткое, опертое или свободное. Жесткое закрепление (нет угловых и линейных перемещений): сварка, пайка, приклеивание, закрепление несколькими винтами. Шарнирная опора (нет линейного перемещения, но возможен поворот по опертой стороне): направляющие, закрепление 1–2 винтами или разъемом. Свободная сторона пластины допускает линейные и угловые перемещения.
Собственная частота пластины с распределенной нагрузкой, Гц :
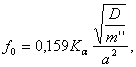 (1.1)
(1.1)
![]()
где Ka – коэффициент определяемый способом крепления пластины и соотношением ее сторон а, в;
![]() D = 0,09Eh3 – жесткость платы, Н·м ;
D = 0,09Eh3 – жесткость платы, Н·м ;
![]() a, в, h – собственно длина, ширина, высота пластины, м ;
a, в, h – собственно длина, ширина, высота пластины, м ;
![]() m'' = m/ав – распределенная по площади масса пластины, кг/м2.
m'' = m/ав – распределенная по площади масса пластины, кг/м2.
![]() Если в центре пластины сосредоточена масса М, а по площади распределена масса пластины m, целесообразно применять формулу :
Если в центре пластины сосредоточена масса М, а по площади распределена масса пластины m, целесообразно применять формулу :
 (1.2)
(1.2)
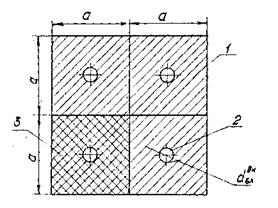
Для пластины с числом точек крепления n = 4, 5, 6
![]() (1.3)
(1.3)
где А = 1/а2 при n = 4 ; А = 4/(а2+в2) при n = 5 ; А = 1/4а2 при n = 6.
Для круглых пластин, жестко закрепленных по контуру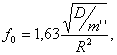 (1.4)
(1.4)
где R – радиус пластины, м; D = 0,09Eh3 – жесткость пластины,
Н·м; m'' = 0,318m/R2 – распределенная по площади массы пластины m.
Величина прогиба Zmax, м, и частота собственных колебаний элемента конструкции f0, Гц, связаны формулой Гейгера:
Повышение прочности можно достичь, используя ребра жесткости, которые должны крепиться не только к пластине, жесткость которой они повышают, но и к опорам конструкции.
Для прямоугольной пластины, свободно опертой по контуру и имеющей ребра жесткости, параллельные осям координат.
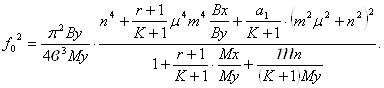 (1.6)
(1.6)
где а в – длина и ширина пластины, м; ах, hx – параметры сечения ребра, параллельного оси Х, м; Вх, By – жесткости ребер, параллельных осям соответственно X и Y, Н·м,
Bx = 0,09Eaxhx3; By = 0,09Eвyhy3;
Mx, My – масса ребер; r, K – число ребер, параллельных осям соответственно X и Y; mn – масса пластины, кг; n, m – число полу волн в направлении осей X и Y; D – цилиндрическая жесткость пластины, Н·м.
![]()
![]()
Если ребра, параллельные оси Y отсутствуют, то
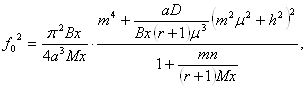 (1.7)
(1.7)
Расчет элементов на прочность следует проводить исходя из основных соотношений теории сопротивления материалов:
при растяжении – сжатии
σр–сж = р/s ≤ [ σ ]р–сж ;
при срезе
tср = р/s ≤ [ t ]ср ;
при изгибе
σи = Мu / W < [ σ]u ;
при кручении
tкр = Мкр / Wp ≤ [ t ]кр,
где Р – усилие действующее на деталь, Н ; S – площадь сечения детали, м2 ; Mu, Mкр – изгибающии и крутящии моменты, Н·м ; W, Wp – моменты сопротивления при изгибе и кручении, м3 .
Таким образом, определение нагрузок сводится к определению сил и моментов, действующих на деталь.
Нагрузки статистического режима :
а) сила тяжести P, H:P = mg, где m – масса элемента, кг; g – ускорение свободного падения g = 9,8 м/с2
б) сумма систем сил (равнодействующая),
![]()
в) момент силы, Н·м ; Mp = Ph ;
г) сумма моментов сил, Н·м :
![]()
д) момент сопротивления сечения W ;
е) момент инерции сечения I.
Нагрузки при вибрациях
P = mgηnn(1.8)
где m – масса детали с учетом массы элементов, закрепленных на ней, кг; g – ускорение свободного падения, м/с2 ; nn – вибрационная перегрузка, действующая на деталь при резонансе ; η – коэффициент динамичности, позволяющий привести задачу к статической,
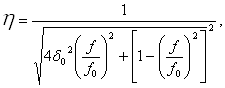 (1.9)
(1.9)
здесь δ0 – параметр, пропорциональный коэффициенту демпфирования β,
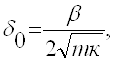 (1.10)
(1.10)
К – жесткость элемента, Н/м, К = 4π2f02m ; f – частота вибраций, Гц ; f0 –частота собственных колебаний элемента, Гц.
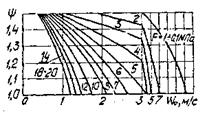
В околорезонансной области частот
 (1.11)
(1.11)
где ψ – логарифмический декремент затухания.
Нагрузки при ударах если принять форму ударного импульса прямоугольной, длительностью τ, то ударную нагрузку можно определить по формуле
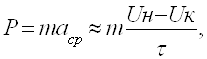 (1.12)
(1.12)
где Uн – начальная скорость элемента конструкции при ударе ; Uк – конечная скорость элемента конструкции при ударе.
Начальную скорость обычно находят из равенства потенциальной и кинетической энергий, например при падении РЭА с высоты
![]()
Скорость в конце удара определяется коэффициентом восстановления Кв.
![]()
Тогда выражение (1.12) принимает вид
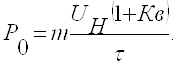 (1.13)
(1.13)
Для более сложных форм ударных импульсов необходимо определить спектр воздействующих частот и рассчитать ударную нагрузку как взвешенную сумму спектральных составляющих.
Для моделей типа балок и пластин при падении конструкции ударная перегрузка
![]() (1.14)
(1.14)
где Н – высота падения, м; Zmax – максимальный прогиб детали, м.
В качестве допускаемых параметров прочности обычно принимают допускаемые механические напряжения в конструкциях.
Допускаемые механическим напряжением называется такое безопастное напряжение, которое деталь может выдержать в течение заданного срока эксплуатации.
Допускаемое напряжение при расчете деталей на прочность определяется по формулам :
[ σ ] = σпред/n и [ t ] = tпред/n,
где σпред, tпред – продельные значения механических напряжений ; n – запас прочности.
Определение запаса прочности при статических нагрузках. При постоянных напряжениях, возникающих при статических нагрузках, прочность хрупкого материала и материала с низкой пластичностью определяется приделом прочности σпред = σв, а пластичного – приделом текучести σпред = σт.
Запас прочности устанавливают в виде произведения частных коэффициентов :
n = n1n2n3, (1.15
где n1 – коэффициент достоверности определения расчетных нагрузок и напряжений ; при повышенной точности n1 = 1,2 – 1,5 ; для оценочных расчетов n1 = 2 – 3 ; n2 –коэффициент, учитывающий степень ответственности детали, обусловливающий требования к надежности ; для мало ответственных и не дорогих деталей n2 = 1 – 1,2, если поломка детали вызывает отказ – n2 =1,3, аварию – n2 =1,5 ; n3 – коэффициент, учитывающий однородность механических свойств материалов, который при статических нагрузках следует выбирать в зависимости от степени пластичности материала (σт/σв) : при σт/σв = 0,49 – 0,55 коэффициент n3 =1,2 – 1,5 ; при σт/σв = 0,55 – 0,70 n3 =1,5 – 1,8 ; при σт/σв = 0,7 – 0,9 n3 =1,8 – 2,2. Для деталей, отлитых из пластмасс, n3 =1,6 – 2,5 ; для хрупких однородных материалов n3 = 3 – 4 ; для хрупких неоднородных материалов n3 = 4 – 6 . При переменных нагрузках для однородных материалов и высокоточных технологий n3 = 1,3 – 1,5, для среднего уровня технологии n3 = 1,5 – 1,7 ; для материалов пониженной однородности n3 = 1,7 – 3.
Прочность при цилиндрических нагрузках. В процессе эксплуатации на детали ботовой, морской, возимой и носимой РЭА в большинстве случаев действуют нагрузки, циклически изменяющиеся по частоте и амплитуде. Следовательно, в них возникают различные циклические напряжения. Необходимо различать следующие основные циклы напряжений:
1) симметричный знакопеременный, когда наибольшие и наименьшие напряжения противоположны по знаку и одинаковы по значению ;
2) асимметичный знакопеременный, когда наибольшие и наименьшие напряжения противоположны по знаку и неодинаковы по значению ;
3) пульсирующий, когда напряжения изменяются от нуля до максимума.
Придел выносливости для симметричных циклов обозначают индексом (–1), для пульсирующих – индексом (0).
Приделы выносливости на изгиб с симметричным циклом :
для стального проката σпред = σ-1=(0,2 –0,3)σв(1+ σ0,2/σв), где σ0,2 – условный придел текучести при статическом растяжении ;
для стального литья и медных сплавов σпред = σ-1=(0,3 –0,4)σв ;
для алюминиевых и магнитных сплавов σпред = σ-1=(0,3 –0,6)σв ;
Приделы выносливости при симметричном цикле связаны ориентировочной зависимостью :
t-1 = (0,5 – 0,7)σ-1 .
Приделы выносливости при пульсирующем и знакопеременном симметрических циклах связаны зависимостями :
при изгибе σпред = σ ≈ (1,4 – 1,6)σ-1 ;
при растяжении σпред = σ0 ≈ (1,5 – 1,8)σ-1(1.16)
Эти зависимости справедливы для деталей, длительное время работающих при циклических нагрузках (свыше 107 циклов).
Если вибрация или удары носят кратковременный характер, допускаемое напряжение при N циклах
σN = σ-1 + 0,167 (σT– σ-1) (в – lgN) (1.17)
Список использованных источников
1. Основы теории цепей: Методические указания к курсовой работе для студентов – заочников специальности 23.01 “Радиотехника”/ Сост. Коваль Ю.А., Праги О.В. – Харьков: ХИРЭ, 2001. – 63 с.
2. Зернов Н.В., Карпов В.Г. “Теория электрических цепей”. Издание 2-е, перераб. и доп., Л.,”Энергия”,2002.
Похожие работы
... 84,4 29 1,7 3,9 15,4 54,5 119,4 210,3 327,1 469,8 833,2 30 35,8 36 37,3 41,4 47,6 55,1 63,4 72,3 91,1 31 2,1 4,4 13,8 41,4 86,4 149,1 229,6 328,1 578,5 2. Расчет прочности печатных плат В соответствии с общей методикой прочностных расчетов для оценки прочности печатной платы необходимо в первую очередь рассчитать основную частоту собственных колебаний платы. ...
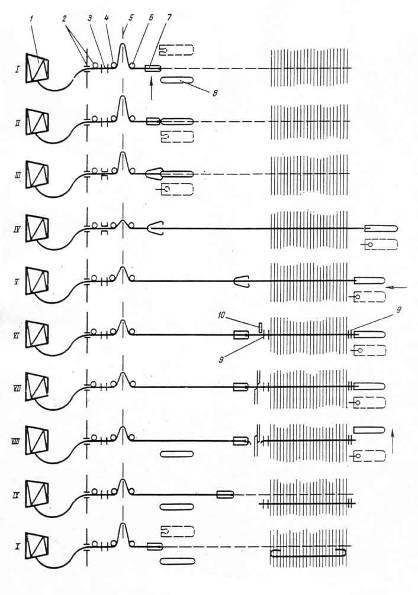
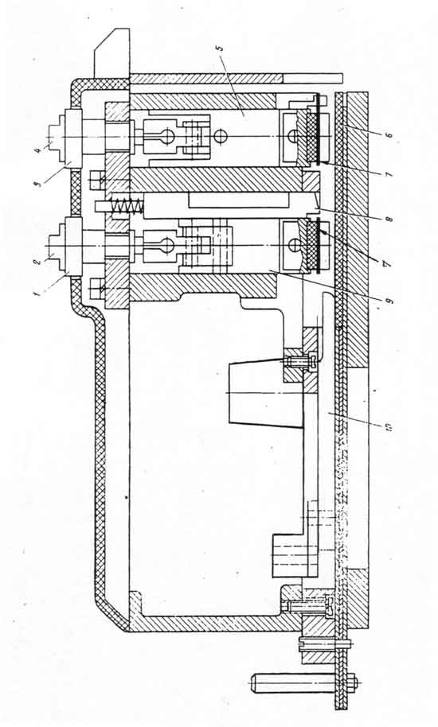
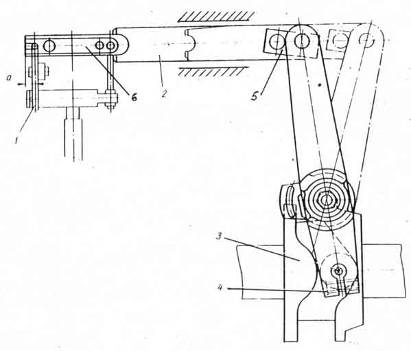
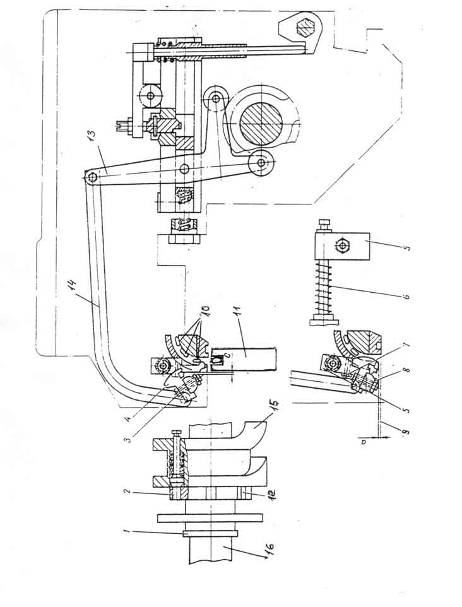
... в своих разработках большое внимание механизмам приемной коробки. Это подтверждает актуальность выбранной темы дипломного проекта по модернизации приемной коробки. Рис. 5а Рис. 5б Рис. 6 Рис. 8а Рис. 8б 1.6 ИССЛЕДОВАНИЕ МЕХАНИЗМА УКЛАДКИ ПРОКЛАДЧИКОВ НА ТРАНСПОРТЕР 1.6.1 КИНЕМАТИЧЕСКОЕ ИССЛЕДОВАНИЕ МЕХАНИЗМА Механизм предназначен для укладки прокладчиков, ...
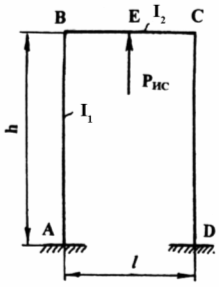
... в заделке (точка В) и момента в точке приложения нагрузки от канатной подвески (точка Е) (2.5) В реальных конструкциях лифтов величина Км ≥ 10, поэтому доля влияния моментов в узлах соединения балок со стойками очень мала, что делает вполне оправданным упрощенный расчет балок и стоек каркаса. 2.1.3 Устройство и расчет пола кабины Горизонтальная рама каркаса ...
... рамках курсового проекта по курсу " Теплогидравлические процессы в ядерных энергетических установках" рассматриваются решения наиболее распространенных задач. 1. ТЕПЛОГИДРАВЛИЧЕСКИЙ РАСЧЕТ ТЕХНОЛОГИЧЕСКОГО КАНАЛА 1.1 Расчет основных геометрических характеристик канала и активной зоны К числу основных геометрических характеристик активной зоны реактора типа РБМК относятся объем и диаметр ...
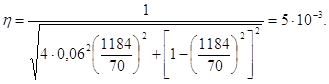

0 комментариев