Курсовая работа:
Режим переконденсации с компактным распределением размеров капель.
Описание проблемы и постановка задачи.
Классические работы Дж.Гиббса, М.Фольмера, Ф.Беккера, В.Дёринга, Я.Френкеля, Я.Зельдовича по физике фазовых переходов I рода относятся к ранним стадиям зарождения новой фазы.
В данной же работе нас интересует процесс конденсации, переходящий из флуктуационного режима роста зародышей новой фазы в стадию переконденсации, именуемую также коалесценцией, или Оствальдовским созреванием [[i]], когда рост крупных капель происходит за счёт растворения более мелких (при условии, что все капли далеки друг от друга).
Режим переконденсации может проходить в одном случае под управлением поглощающей способности поверхности (теория Вагнера: [[ii]]), когда длина свободного пробега 
молекулы много больше радиуса капли 
, а в другом случае под управлением диффузии в паре (теория Лифшица-Слёзова: [[iii], [iv]]), когда 
.
Причиной расхождения эксперимента с теорией Лифшица-Слёзова-Вагнера оказалось допущение неограниченного объёма кластеров новой фазы [[v]].
Поэтому все дальнейшие теоретические исследования Оствальдовского созревания предполагают компактное основание распределения капель по размерам [[vi], [vii], [viii]].
Поэтому задачей данной работы является описание уравнений и параметров режима переконденсации в условиях существования максимального размера капли.
Коалесценция имеет большое практическое значение, например, в образовании и стабильности поверхностей [[ix], [x], [xi]].
Оглавление
Описание проблемы и постановка задачи. 1
Оглавление. 2
1). Переписывание уравнений в терминах максимальной капли. 3
2). Соотношения интегральных моментов функции распределения. 5
3). Нахождение автомодельной функции распределения. 6
4). Нормировка функции распределения. 9
5). Предельный случай – распределение Лифшица-Слёзова. 10
6). Графики. 11
7). Литература. 12
8) Ссылки. 12
1). Переписывание уравнений в терминах максимальной капли.
Оригинальные уравнения теории переконденсации записываются в терминах отношения безразмерного радиуса капли к её критическому радиусу в зависимости от безразмерного времени: 
. Наша задача – переписать их в терминах отношения радиуса капли к максимальному радиусу: 
.
Уравнение роста радиуса капли в режиме коалесценции Лифшица-Слёзова:
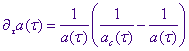(1.1)
Тогда уравнение непрерывности для функции распределения по размерам капель:
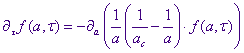(1.2)
Подставляем сюда асимптотический анзац Лифшица-Слёзова в новых переменных и с явной зависимостью от времени:
(1.3)
Преобразуем дифференциальное уравнение (обозначая 
):
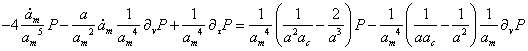
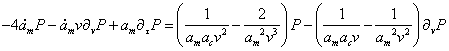
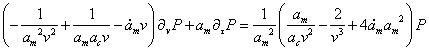
Введём
(1.4)
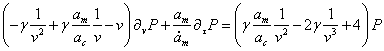
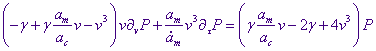(1.5)
Избавимся от 
, подставив 
в уравнение роста радиуса капли (1.1):
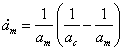
(1.6)
С учётом этого, а также определения 
в (1.4), докажем, что 
является корнем кубического полинома:
(1.7)
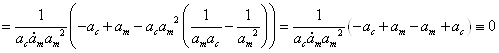
Тогда (1.5) окончательно запишется следующим уравнением на функцию распределения:
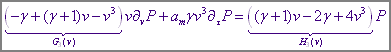(1.8)
Зная один корень, найдём делением по схеме Горнера квадратичное выражение в 
| корень 1 |
|
|
|
|
|
| -1 | 0 |
|
| ||
|
|
|
|
| остаток | |
| -1 |
|
|
|
остаток = нулю
Таким образом:
Решим квадратное уравнение, полагая корни существующими:
Тем самым мы разложили на множители 
, где
(1.9)
Каждая скобка в таком виде разложения, как мы увидим далее, будет положительна. Заметим также, что 
(так что
), что, впрочем, сразу следует из теоремы Виета для 
по отсутствию квадратичного члена.
Итак, уравнение (1.8) запишется следующим образом:
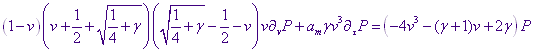(1.10)
В этой работе мы рассмотрим автомодельную функцию 
, не зависящую явно от времени, при этом в полученном дифференциальном уравнении опускается член 
с частной производной по времени от функции распределения.
2). Соотношения интегральных моментов функции распределения.
Соотношения между интегральными моментами функции распределения можно найти, не зная её явного вида. Для этого проинтегрируем от 0 до 1 левую и правую части дифференциального уравнения (1.8), опуская член с производной по времени и вводя моменты:
(2.1)
Интегрируем по частям левую часть:
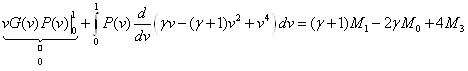
(2.2)
Это выражение, в сущности, означает, что 
, а если вспомнить отношение (1.6) между максимальным и критическим радиусами капли, то получим равенство среднего и критического радиусов:
(2.3)
, когда функция распределения нормирована на единицу (см. пункт 4)
3). Нахождение автомодельной функции распределения.
По-прежнему полагая автомодельным и убирая в (1.10) член с производной по времени, можно явно решить дифференциальное уравнение интегрированием:
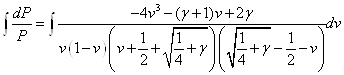(3.1)
Для этого разложим подынтегральное выражение на простейшие дроби и найдём коэффициенты:
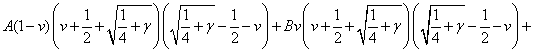
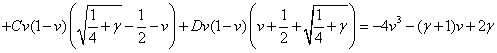
При 
:
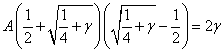
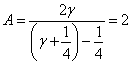
При :
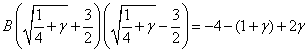
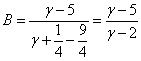
Приравнивание коэффициентов при 
:
Приравнивание коэффициентов при 
(находим 
):
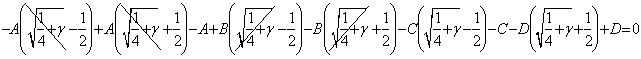
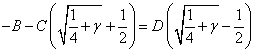
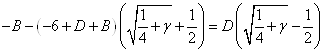
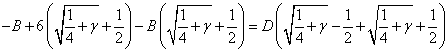
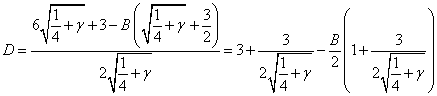
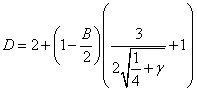(3.2)
Подставляя полученное выражение для 
, выразим только через 
и избавимся от иррациональности в знаменателе:
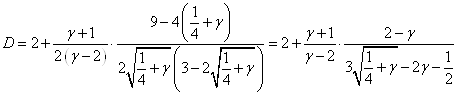
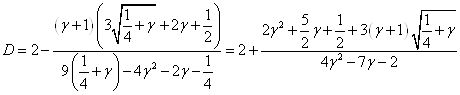
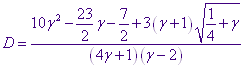(3.3)
Таким образом, найдены все коэффициенты в разложении на простые дроби подынтегрального выражения в (3.1), интегрируя их, получаем, помня об области определения переменных:
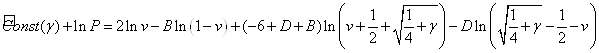
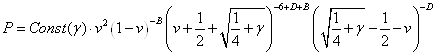
В значениях 
(третий корень ) из (1.9) окончательно запишем:
(3.4)
Где в силу физической ограниченности функции распределения на конце интервала, полагаем:
(3.5)
Оценим
выражение для из (3.2):
(3.6)
Дифференцированием (3.3) и грубой оценкой можно увидеть, что монотонно убывает по из бесконечности, как и 
. При этом величина 
, фигурирующая в (3.4), остаётся ограниченной (не имеет особенности при 
), более того почти постоянной в заданном интервале , в чём можно убедиться, вычитая в форме (3.6) из 
и выражая всё через :
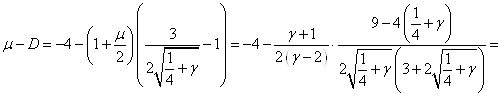
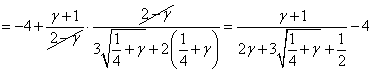
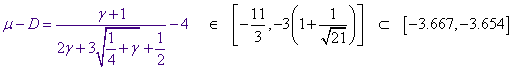(3.7)
Как в пункте 2 проинтегрируем от 0 до 1 левую и правую части (1.8) (без члена с производной по времени), предварительно разделив их на :
Формально интегрируем по частям левую часть:
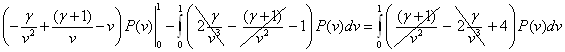
Удовлетворяя условию нормировки, подставим 
из (3.4). При сохранится только первый член:
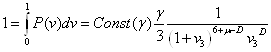
(4.1)
Так что функция распределения (3.4) в нормированном виде равна:
(4.2)
Из самого( /) дифференциального уравнения (1.10) легко выписать производную функции распределения:
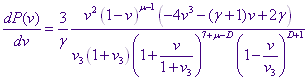(4.3)
Приравняв её нулю и решая каноническое кубическое уравнение 
по формуле Кардано, имеем для максимума функции распределения, изменяющего своё положение с изменением :
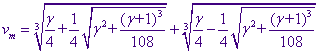(4.4)
5). Предельный случай – распределение Лифшица-Слёзова.
Рассмотрим предельный случай при 
. При этом из (3.3) 
, а из (3.5) 
. Тогда как их разность 
, что было показано в (3.7). Нам также пригодится асимптотика: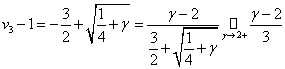 
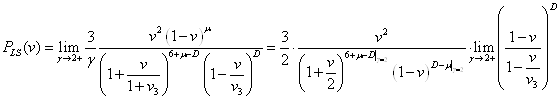
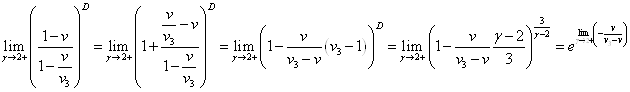
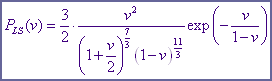(5.1)
Приведём для сравнения функцию Лифшица-Слёзова, записанную в оригинальных переменных 
:
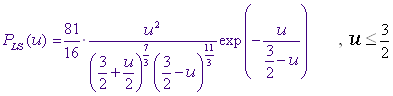(5.2)
6). Графики.
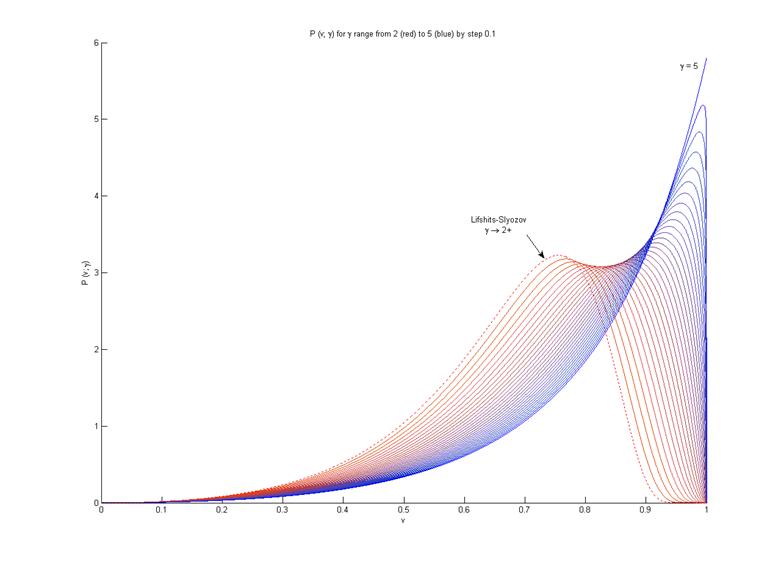
Здесь нарисованы функции распределения 
из (4.2), охватывающие весь интервал возможных вплоть до функции Лифшица-Слёзова (5.1).
Литература.
1. А.Н.Васильев, А.К.Казанский, Л.Ц.Аджемян: «Переконденсация пересыщенного пара: аналитические теории и численный эксперимент».
2. П.Губанов, Ю.Желтов, И.Максимов, В.Морозов: «Кинетический кроссовер режимов коалесценции в пересыщенном однородном растворе».
3. В.Бойко, Х.Могель, В.Сысоев, А.Чалый «Особенности метастабильных состояний при фазовых переходах жидкость-пар»
4. В.Ф.Разумов: «Курс лекций по синергетике».
5. Е.М.Лифшиц, Л.П.Питаевский: «Физическая кинетика».
6. B.Giron, B.Meerson, P.V.Sasorov: «Weak selection and stability of localized distributions in Ostwald ripening».
7. V.M.Burlakov: «Ostwald Ripening on nanoscale».
8. B.Niethammer, R.L.Pego: «Non-self-similar behavior in the LSW theory of Ostwald ripening».
Перечисленные и многие другие материалы по теме временами доступны по ftp здесь: ftp://rodion.homeftp.net 
Work =Учёба= Кафедра статфизики =Курсовая= Литература
Ссылки
[i] W.Z.Ostwald // Phys. Chem. 37, 385 (1901)
[ii] C.Z.Wagner // Electrochem. 65, 581 (1961)
[iii] М.Лифшиц, В.Слёзов // ЖЭТФ 35, 479 (1958)
[iv] M.Lifshitz, V.Slyozov // J.Phys.Chem.Solids 19, 35 (1961)
[v] J. Alkemper, V.Snyder, N.Akaiwa, P.Voorhees // Phys.Rev.Lett. 82, 2725 (1999)
[vi] N.Akaiwa, P.Voorhees // Phys.Rev.B 49, 3860 (1994)
[vii] D.Fan, S.Chen, L.Chen, P.Voorhees // ActaMaterialia 50, 1895 (2002)
[viii] K.Wang, M.Gliksman, K.Rajan // Comput.Mat.Sci. 34, 235 (2005)
[ix] S.Kukushkin, A.Osipov // Progress in Surf. Sci. 51, 1 (1996)
[x] M.Zinke-Allmang, L.Feldman, M.Grabow // Surf. Sci.Rep. 16, 377 (1992)
[xi] W. Bartelt, C.Theis, M.Tromp // Phys.Rev. B 54, 11741 (1996)
0 комментариев