Задача №1.
Необходимо построить рекуррентный алгоритм моделирования, нормального случайного процесса, с заданной корреляционной функцией.
Метод решения, на основе факторизации.
Дано.
R(t) =
;
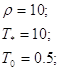при 
;
Корреляционная функция стационарного, случайного процесса с рациональным спектром, имеет вид:
R(
)=;
следовательно система.
Корреляционная функция соответствующего дискретного процесса равна:
R[n]=
где 
; 
;
где 
; fb=
fb=20; 
Отсюда найдем:
; 
; 
; 
;
Не нарушая общности рассуждений, положим 
, тогда R[0]=1. Запишем функцию R[n] для n
0 в комплексной форме:
;
; 
; 
;
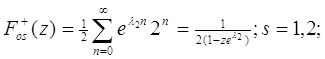
Отсюда
;
Следовательно, спектральная функция F(z) в соответствии имеет вид.
;
После приведения к общему знаменателю и приведения подобных членов получим.
;
где
, 
;
Знаменатель F(z) представляет собой произведение двух сомножителей требуемой формы, т.е. в факторизации знаменателя нет надобности. Это всегда будет иметь место при использовании такой последовательности подготовительной работы.
Для факторизации числителя найдем его корни:
;
;
В данном случае ввиду симметрии уравнения
;
анализ корней для уяснения величины их модуля не потребуется, и в качестве корня 
окончательного выражения вида брать любой из корней 
. В этом можно убедится, подставив в уравнение 
вместо значения корней. Действительно, уравнение обращается в тождество при 
.
Таким образом, дискретная передаточная функция формирующего фильтра и рекуррентный алгоритм для моделирования случайного процесса с корреляционной функцией 
имеют соответствующий вид
;
; где
, 
;
; 
;
;
; 
;
.
Задача №2.
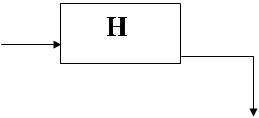
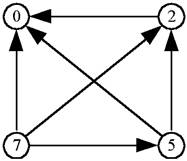
Дана структура нелинейного фильтра, схема которого представлена выше.
 | ||||
 | ||||
 | ||||
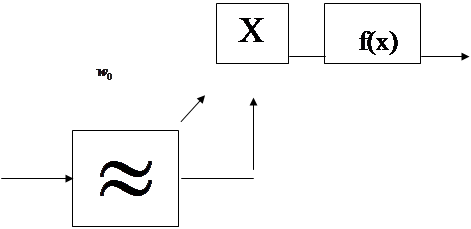
Схема измерительной структуры представлена выше.
;
;
Список литературы
Для подготовки данной работы были использованы материалы с сайта http://www.cooldoclad.narod.ru/
Похожие работы
... и человеку. Как видите, немалую роль в решении проблемы сохранения жизни на Земле играет математика с ее методом математического моделирования. Итак, при объяснении метода математического моделирования и его применения к решению экологических задач реализуется практическая направленность обучения, поскольку математический метод применяется к разрешению жизненной, практической, глобальной (!) ...
... задач. Однако это не так. Его эффективность можно проиллюстрировать таким примером. В 1986 г. Центральное телевидение организовало серию научно-публицистических передач «Требуется идея» (с целью популяризации методов решения творческих задач). Одна из этих телепередач была посвящена «мозговому штурму». Во время передачи нужно было «дать совет Робинзону», как вытащить к берегу из лесу лодку, ...
... . 3): Рис. 3 c = a·b. В силу обратимости операций умножения и деления можно найти a = c/b или b = c/a. Моделью решения сюжетной задачи является дерево. Оно характеризует структуру решения сюжетной задачи и сложность решения, отождествляемую со сложностью дерева: = 2·3 = 6. Структурными элементами решения задачи являются вершины дерева. Задача I.2. Из двух пунктов навстречу друг другу ...
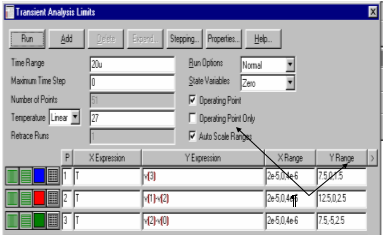
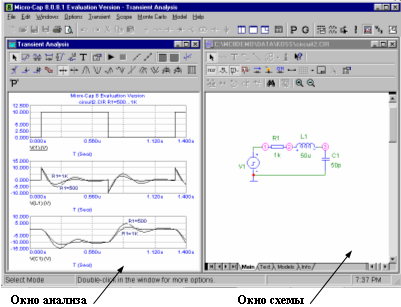
... графики переходных процессов, заданных для анализа величин (напряжений в узлах схемы, падений напряжений на двухполюсных элементах, токов в ветвях схемы и т.п.). На рис. 2 показан результат моделирования переходных процессов в пассивной линейной цепи второго порядка, электрическая схема которой приведена в правом окне. Рис. 2 В окно анализа выведены следующие графики: V(1) – импульсный ...
0 комментариев