Задача №1
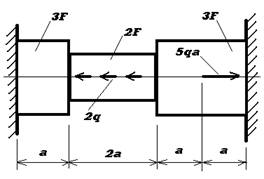
а = 0,5 м
q = 10 kH/м
F = 2,5 cм2
Е = 2×105 Мпа
DL -?, N -?, s -?
Решение.
Данная задача является статически неопределимой, так как её нельзя решить при помощи только уравнений статики (уравнений равновесия). Недостающее уравнение составим из условия деформаций. Для этого отбросим одну из заделок (правую) и заменим её действие неизвестной реактивной силой Х. Реакцию левой опоры примем R.
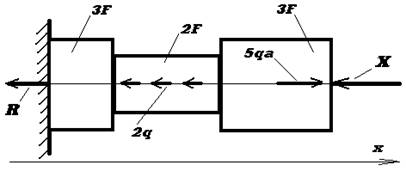
В данном случае можно составить только одно уравнение равновесия:
SХ = 0; 5qa - 2q×2a - R - X = 0;
X + R = qa (1)
Дополнительное уравнение составляем из условия, что общая длина стержня с жесткими заделками по концам не может измениться, следовательно: DL = 0:
Общее удлинение DL найдем как сумму удлинений от каждой из сил. Реактивная сила Х сжимает все три части составного стержня. Сосредоточенная сила 5qa растягивает левую и среднюю части, а также половину правой части стержня. Нагрузка 2q как равномерно распределенная сжимает среднюю часть стержня, затем как сосредоточенная сила 2q×2a сжимает левую часть. Реакция левой заделки R не влияет на деформацию стержня. Таким образом, имеем:
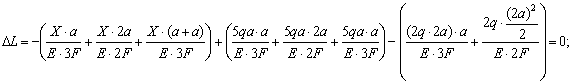
![]()
2Х×а + 5qa2 = 0; X = 2,5×qa = 2,5×10×0,5 = 12,5 Кн
Из уравнения (1) находим:
R = qa - 2,5×qa = -1,5×qa = -1,5×10×0,5 = -7,5 Кн
Знак "минус" свидетельствует о том, что реакция левой заделки направлена в противоположную сторону от той, которую мы приняли произвольно. Реакция правой заделки равна реактивной силе Х, но направлена в противоположную сторону.
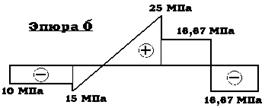
Зная реакции заделок и действующие нагрузки, строим эпюру внутренних сил N:
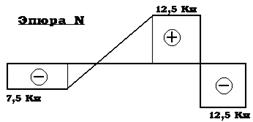
Для построения и эпюры напряжений s делим значение внутренней силы в каждой точке на площадь сечения. В местах изменения поперечного сечения будут происходить скачки напряжения из-за резкого изменения площади:
Похожие работы
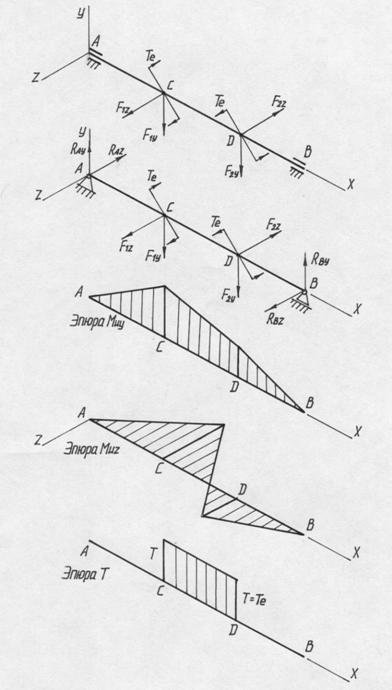
... крутящий момент. Иногда обозначение заменяют на или , более точно отвечающие физическому смыслу этой величины. График, показывающий как меняется внутренний силовой фактор по длине рассматриваемого тела, называется эпюрой. Правильность построения эпюры обеспечивается, в первую очередь, надлежащим выбором характерных сечений, то есть тех сечений, в которых величина внутреннего силового фактора ...
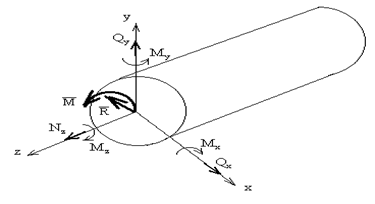
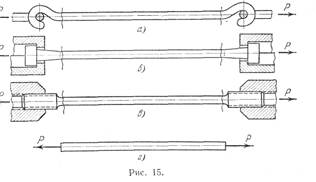
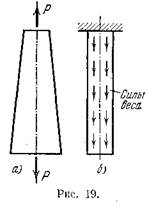
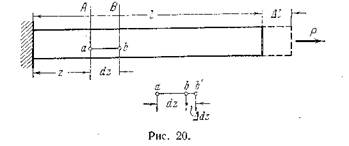
... процессов разрушения материалов или при исследовании поведения длинных и тонких стержней, для которых сжатие сопровождается, как правило, изгибом. Рассмотрим напряжения, возникающие в поперечном сечении растянутого стержня. Нормальная сила N является равнодействующей внутренних сил в сечении (рис. 17). Естественно предположить, что для однородного стержня внутренние силы распределены по ...
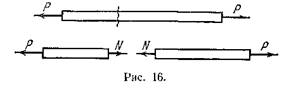
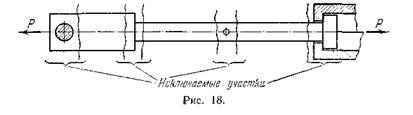
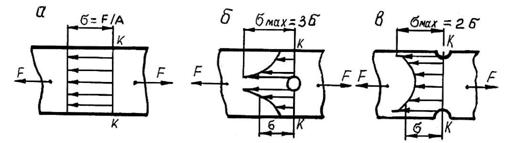
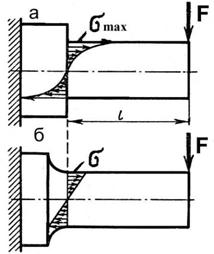
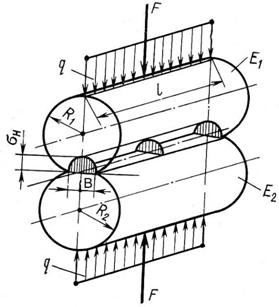
... Из выражений (4) и (5) можно найти значение осевого момента сопротивления W поперечного сечения вала как или и далее величину диаметра вала . Местные напряжения Напряжения при растяжении (сжатии), изгибе, кручении и сложных деформациях, определяемые по рассмотренным выше зависимостям, называют расчетными или номинальными. Экспериментально установлено, что в местах приложения сил, в местах ...
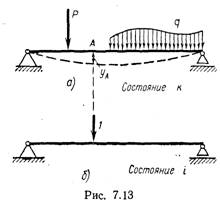
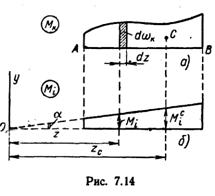
... , представленное на рис. 7.18, в. В точке А приложена единичная вертикальная сила, направленная вниз. Эпюра изгибающих моментов для этого состояния представлена на рис. 7.18, в. Определяем вертикальное перемещение по методу Мора, используя способ перемножения эпюр. Так как на вертикальном стержне во вспомогательном состоянии эпюра М1 отсутствует, то перемножаем только эпюры, относящиеся к г

0 комментариев