Министерство образования и науки Украины
Моделирование пассивных и активных фильтров
ЦЕЛЬ РАБОТЫ
Пользуясь программной средой Electronics Workbench смоделировать: пассивные фильтры низкой частоты (ФНЧ), однозвенные и двухзвенные; пассивные фильтры высокой частоты (ФВЧ), однозвенные и двухзвенные; полосовой и режекторный фильтры (ППФ); активный ФНЧ на ОУ; активный ФВЧ на ОУ; полосовой фильтр активного типа.
С помощью программы FilterLab построить АЧХ и ФЧХ, смоделировать электрические схемы для фильтров Баттерворта и Чебышева.
ХОД РАБОТЫ
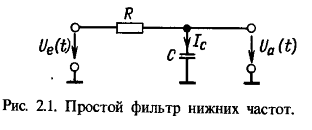
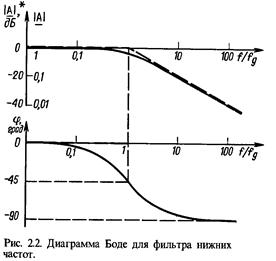
1. Параметры элементов однозвенного пассивного ФНЧ рассчитываются, исходя из требуемой частоты среза f0 и принятого волнового сопротивления р. В рассматриваемом примере имеем при f0 = 10 000 Гц и ![]() = 8 Ом:
= 8 Ом:
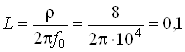 мкГн,
мкГн,
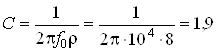 мкФ.
мкФ.
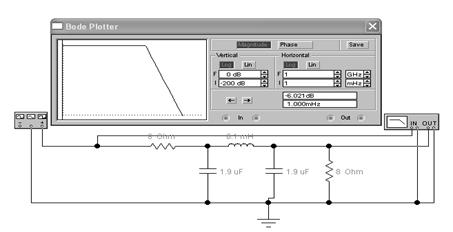
Рисунок 1 - Пассивный фильтр низкой частоты (ФНЧ), однозвенный.
В случае двухзвенного фильтра по сравнению с однозвенным, удается получить характеристику с более крутым фронтом.
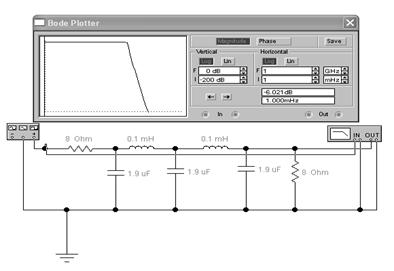
Рисунок 2 - Пассивный фильтр низкой частоты (ФНЧ), двухзвенный.
2. Параметры элементов однозвенного ФВЧ рассчитываются, исходя из требуемой частоты среза f0 и принятого волнового сопротивления р. В рассматриваемом примере имеем при f0= 300 Гц и ![]() = 8 Ом:
= 8 Ом:
![]() мкГн,
мкГн,
![]() мкФ.
мкФ.
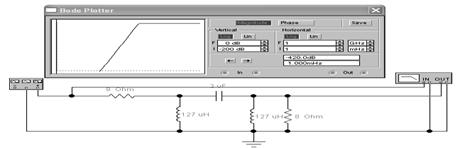
Рисунок 3 - Пассивный фильтр высокой частоты (ФВЧ), однозвенный.
В случае двухзвенного фильтра, по сравнению с однозвенным, удается получить характеристику с более крутым фронтом.
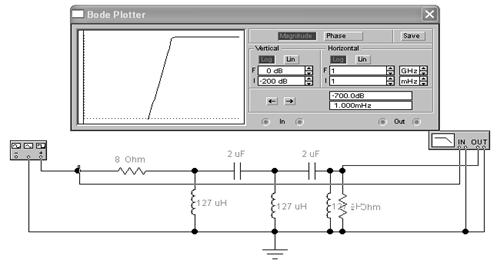
Рисунок 4 - Пассивный фильтр высокой частоты (ФВЧ), двухзвенный.
3. Параметры элементов двухконтурного полосового фильтра рассчитываются, исходя из центральной частоты фильтра f0. При С = 1000*10-9 Ф и L = 0,25 мкГн имеем:
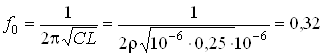 МГц.
МГц.
Далее резонансные частоты контуров раздвигаются, для чего емкость одного увеличивается на 1-2 %, другого - уменьшается. Чем шире должна быть получена полоса пропускания фильтра, тем больше это изменение емкости.
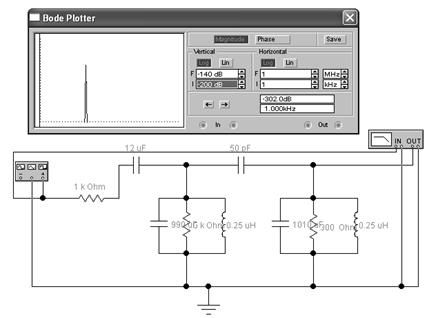
Рисунок 5 - Полосовой фильтр.
4. Параметры элементов трехконтурного режекторного фильтра, как и в предыдущем случае, рассчитываются исходя из центральной частоты фильтра f0. В рассматриваемом случае центральная частота f0 = 0.32 МГц.
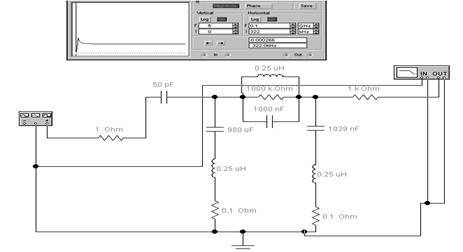
Рисунок 6 - Режекторный фильтр.
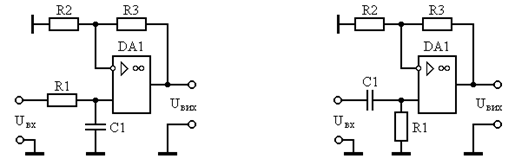
5. Комплексный коэффициент активного ФНЧ 1-го порядка определяется выражением:
![]()
для модуля коэффициента передачи имеем:
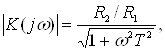
где Т = R2C2 - постоянная времени фильтра.
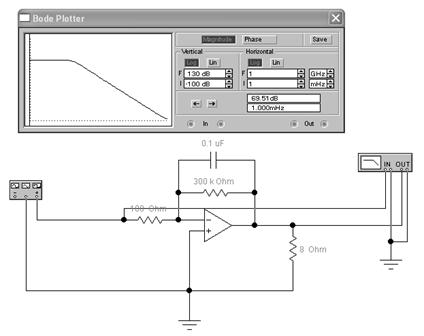
Рисунок 7 - Активный ФНЧ на ОУ.
6. для модуля коэффициента передачи активного ФВЧ имеем
![]()
где Т = R1C1 - постоянная времени фильтра.
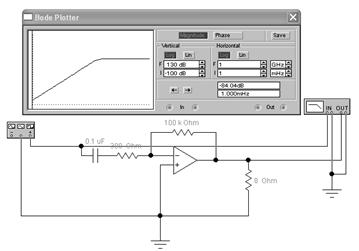
Рисунок 8 - Активный ФВЧ на ОУ.
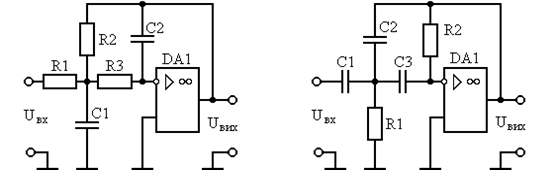
7. Комплексный коэффициент активного фильтра 2-го порядка определяется выражением:
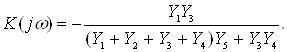
Проводимости равны:
Y1 = g1 = 1/R1, Y2 = g2 = 1/R2, Y3 = j![]() C3, Y4 = j
C3, Y4 = j![]() C4, Y5 = g5 = 1/R5.
C4, Y5 = g5 = 1/R5.
При данных величинах для модуля комплексного коэффициент передачи равен:
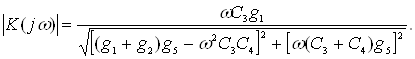
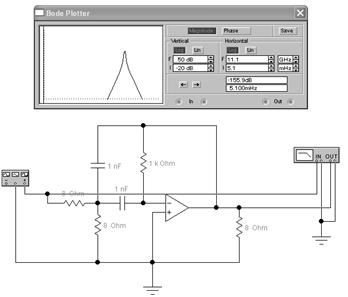
Рисунок 9- Полосовой фильтр активного типа.
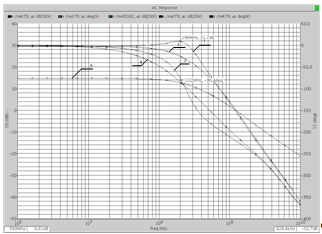
АЧХ и ФЧХ для ФНЧ 1-го порядка Баттерворта и Чебышева:
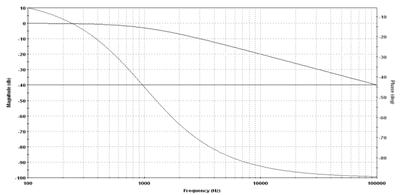
Рисунок 9- АЧХ и ФЧХ.
Электрическая схема:
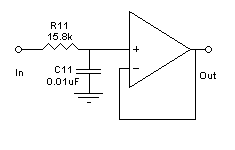
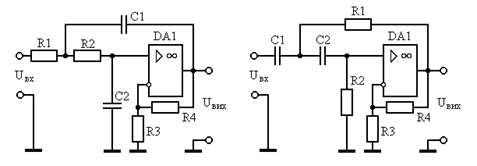
Рисунок 10 - Электрическая схема.
АЧХ и ФЧХ для ФНЧ 2-го порядка Баттерворта и Чебышева:
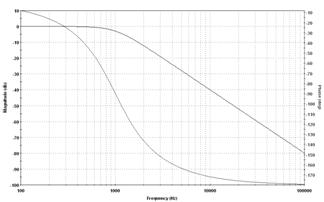
Рисунок 11- АЧХ и ФЧХ.
Электрическая схема:
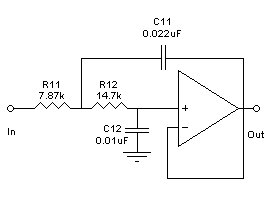
Рисунок 12 - Электрическая схема.
8. АЧХ и ФЧХ для ФВЧ 1-го порядка Баттерворта и Чебышева: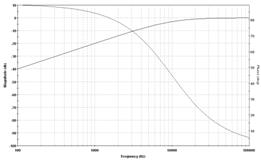
Рисунок 13 - АЧХ и ФЧХ.
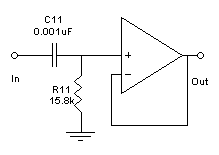
Рисунок 14 - Электрическая схема
АЧХ и ФЧХ для ФВЧ 2-го порядка Баттерворта и Чебышева:
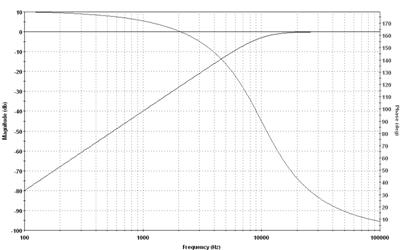
Рисунок 15 - АЧХ и ФЧХ.
Электрическая схема:
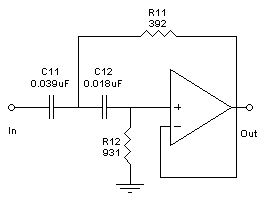
Рисунок 16 - Электрическая схема
Таблица 1.1- Расчет фильтров 2-го порядка при f=150 KHz
| Фильтр | С=, nF | R1=, KОм | R2=, KОм | Rfb=,KОм |
| Bessel | 1 | 0.779 | 2.338 | 6.234 |
| Butterworth | 1 | 0.750 | 1.501 | 4.502 |
| Chebyshev (0.5 dB Ripple) | 1 | 0.779 | 1.045 | 3.648 |
| Chebyshev (1 dB Ripple) | 1 | 0.815 | 0.891 | 3.411 |
| Chebyshev (2 dB Ripple) | 1 | 0.898 | 0.705 | 3.207 |
| Chebyshev (3 dB Ripple) | 1 | 0.996 | 0.585 | 3.163 |
Выводы
В ходе лабораторной работы мы ознакомились со схемотехническими особенностями различных типов фильтров.
Определили то, что АЧХ фильтра должна приближаться к идеальной, а затухания, вносимые им, быть минимальными.
Пассивные фильтры вносят большие затухания по сравнению с активными фильтрами, однако имеют простоту в схемотехническом решении и расчёте составляющих его деталей.
Данные типы фильтров нашли широкое применение в широкополосных усилителях и акустике, которые имеют раздельные тракты НЧ, СЧ, ВЧ.
Похожие работы
... = 6,66 на различные уровни входного гармонического воздействия Рис. Реакция схемы при Q = 10,8 на различные уровни входного гармонического воздействия 5. Синтез ФНЧ третьего порядка с дополнительными RC-цепями Фильтры нижних частот в СВЧ диапазоне образуют отдельный и важный в практическом отношении класс устройств частотной селекции. Достаточно отметить каналообразующие фильтры при ...
выполнить расчёт и моделирование четырёх активных фильтров. 1. Определить необходимый порядок фильтра. 2. Выполнить расчёт основных параметров фильтра, получить выражение для коэффициента передачи в функции частоты. 3. Используя MathCad построить желаемую ЛАЧХ 4. Составить принципиальную схему и рассчитать. 5. Выбрать активные и пассивные элементы ...
... программы. ………..……………………………………………………………………………….12 6. Расчет частотных характеристик с использованием пакета «Electronics Workbench Pro». ………………16 7. Заключение. …………………………………………………………………………………………………….18 8. Список литературы. …………………………………………………………………………………………...19 1. Выбор схемной реализации фильтра, разработка его ...
... пропускают или задерживают сигналы, лежащие в определённых полосах частот. Фильтры можно классифицировать по их частотным характеристикам: 1. Фильтры нижних частот (ФНЧ) – пропускают все колебания с частотами не выше некоторой частоты среза и постоянную составляющую. 2. Фильтры верхних частот (ФНЧ) – пропускают все колебания не ниже некоторой частоты среза. 3. Полосовые фильтры (ПФ) – ...
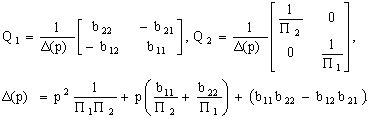


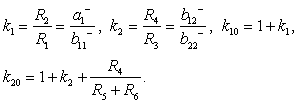
0 комментариев