Cтатистическая надежность регрессионного моделирования

Вариант 4-1

1. Рассчитайте параметры уравнения линейной регрессии

2. Оцените тесноту связи с помощью показателей корреляции и детерминации

3. Определите среднюю ошибку аппроксимации. Сделайте выводы

4. Оцените статистическую надежность регрессионного моделирования с помощью F-критерия Фишера и t-критерия Стьюдента

5. Оцените полученные результаты, оформите выводы

№ набл.	Район	Средний размер назначенных ежемесячных пенсий, тыс.руб., y	Прожиточный минимум в среднем на одного пенсионера в месяц, тыс.руб., x
1	Брянская обл.	240	178
2	Владимирская обл.	226	202
3	Ивановская обл.	221	197
4	Калужская обл.	226	201
5	Костромская обл.	220	189
6	г.Моска	250	302
7	Москавская обл.	237	215
8	Орловская обл.	232	166
9	Рязанская обл.	215	199
10	Смоленская обл.	220	180
11	Тверская обл.	222	181
12	Тульская обл.	231	186
13	Ярославская обл.	229	250
Fтабл.=4,84(α =0,05)		=9,29	=34,75

1. Расчет параметров уравнения линейной регрессии по данным таблицы:

Решение:

1. Уравнение линейной регрессии имеет следующий вид:

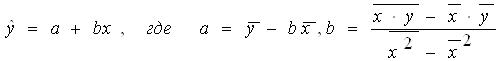
№ наблюдения	х	y	X2	X·Y		yx	y- yx	Ai
1	178	240	31684	42720		222,51	17,49	7,29
2	202	226	40804	45652		227,67	-1,67	0,74
3	197	221	38809	43537		226,59	-5,59	2,53
4	201	226	40401	45426		227,45	-1,45	0,64
5	189	220	35721	41580		224,87	-4,87	2,22
6	302	250	91204	75500		249,17	0,83	0,33
7	215	237	46225	50955		230,46	6,54	2,76
8	166	232	27556	38512		219,93	12,07	5,20
9	199	215	39601	42785		227,02	-12,02	5,59
10	180	220	32400	39600		222,94	-2,94	1,34
11	181	222	32761		40182	223,15	-1,15	0,52
12	186	231	34596		42966	224,23	6,77	2,93
13	250	229	62500		57250	237,99	-8,99	3,93
Сумма	2646	2969	554262		606665
Ср. значение	203,54	228,38	42635,54		46666,54			2,77

Найдем b:

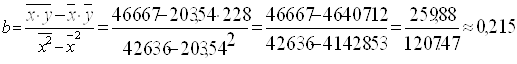
Тогда

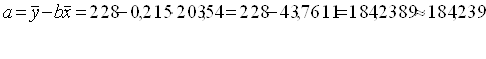
Уравнение линейной регрессии имеет вид:

ŷ_x =184,239+0,215x

2. а) Рассчитываем коэффициент корреляции:

по формуле:

r_xy= b — = 0,21 =0,78

с помощью статистической функции КОРРЕЛ-r =0,78

Связь между переменными x и y прямая, средняя, близкая к сильной, т.е. величина среднемесячной пенсии в значительной мере зависит от прожиточного минимума в среднем на одного пенсионера в месяц

б) Для определения средней ошибки аппроксимации рассчитываем столбцы

y_x, y- y_x, A_i:

A_i= y- y_x* 100, А = 1/n∑ⁿ_i=1 A_i

Получаем значение средней ошибки аппроксимации

А = 2,77%

Величина ошибки аппроксимации говорит о хорошем качестве модели.

в) Величина коэффициента детерминации получена с помощью функции

ЛИНЕЙН R² =r_xy² = 0,61,

то есть в 61% случаев изменения среднемесячного прожиточного минимума на одного пенсионера приводят к изменению среднемесячной пенсии. Другими словами – точность подбора регрессии 61 % - средняя.

3. Оценка статистической значимости

а) по критерию Фишера:

1. Выдвигаем нулевую гипотезу о статистической незначимости параметров регрессии и показателя корреляции а = b = r_xy=0;

2. Фактическое значение критерия получено из функции ЛИНЕЙН

∑(ỹx-y)²/m r²xy0,61

Fфакт= = (n-2) = (13-2) = 1,56*11 = 17,2;

∑(y-ỹ)² /(n-m-1) 1-r²xy 1-0,61

3. F_табл =4,84

4. Сравниваем фактическое и табличное значения критерия Fфакт> F_табл , т.е.нулевую гипотезу отклоняем и делаем вывод о статистической значимости и надежности полученной модели.

б) по критерию Стьюдента:

1. Выдвигаем гипотезу о статистически незначимом отличии показателей от нуля: a = b = r²xy = 0;

2. Табличное значение t – критерия зависит от числа степеней свободы и заданного уровня значимости α. Уровень значимости – это вероятность отвергнуть правильную гипотезу.

rxy √(n-m)

t=

√(1- r²_xy)

Где n – количество наблюдений; m – количество факторов.

t= 0,78√(13-2)= 2,59=4,18

√(1-0,61)0,62

3. Фактические значения t-критерия рассчитываются отдельно для каждого параметра модели. С этой целью сначала определяются случайные ошибки параметров mа , mb, mr_xy.

mа=Sост √∑х² = 1,65;

mb= Sост = 0,004

nσх σх√n

mr_xy= √(1- r²_xy) = 0,062

n-m-1

где Sост=√(∑ (y- y_x)) = 5 = 0,5

n-m-110

Рассчитываем фактические значения t – критерия:

tфа =a/ mа =111,66

tфb =b/ mb =53,75

tфr_xy= r_xy/mr_xy = 12,58

tфа>tтабл ; tфb>tтабл ; tфr_xy >tтабл . Нулевую гипотезу отклоняем , параметры a, b, r_xy- не случайно отличаются от нуля и являются статистически значимыми и надежными.