Задание 1. По исходным данным построить дискретный ряд распределения по группировочному признаку. Для целей анализа и сравнения применить характеристики центра группирования, к которым относятся средняя арифметическая, мода и медиана. Для характеристики степени отклонения распределения частот от симметричной формы рассчитать показатели эксцесса и ассиметрии. Проанализировать полученные значения показателей центра распределения и формы распределения. Сформулировать вывод.
Таблица 1 - Основные показатели деятельности предприятия за период «N»
| № п/п | Выручка от продажи товаров, т.р. | Прибыль от продаж, т.р. | Чистая прибыль отчетного периода,т.р. | Основные средства,т.р. | Запасы, т.р. | Денежные средства, т.р. |
| 4 | 344280 | 24774 | 22364 | 106447 | 28423 | 6329 |
| 5 | 107843 | 9210 | 7850 | 92805 | 26458 | 1341 |
| 6 | 105600 | 4678 | 5076 | 52187 | 9844 | 3107 |
| 7 | 198771 | 13115 | 11429 | 46234 | 82938 | 2011 |
| 8 | 85000 | 4809 | 5862 | 56932 | 27850 | 1329 |
| 9 | 62000 | 2381 | 1523 | 47067 | 26781 | 1378 |
| 10 | 171647 | 65920 | 24971 | 54356 | 21342 | 1901 |
| 11 | 45499 | 7659 | 8124 | 29351 | 84013 | 6082 |
| 12 | 110690 | 4817 | 1478 | 62651 | 10328 | 1638 |
| 13 | 32106 | 1089 | 941 | 40633 | 23805 | 4999 |
| 14 | 71587 | 20995 | 18180 | 64567 | 11774 | 1576 |
| 15 | 21980 | 5515 | 3030 | 58711 | 11559 | 2387 |
| 16 | 24690 | 10786 | 13123 | 87210 | 32952 | 6031 |
| 17 | 56341 | 3412 | 2271 | 57195 | 20645 | 1299 |
| 18 | 56000 | 2014 | 2017 | 33465 | 54864 | 3757 |
| 19 | 45700 | 7469 | 6154 | 32176 | 23256 | 6222 |
| 20 | 183600 | 38983 | 1170 | 11553 | 76561 | 8854 |
| 21 | 21197 | 2586 | 2189 | 40150 | 13942 | 1537 |
| 22 | 24446 | 6310 | 1776 | 13488 | 74681 | 3136 |
| 23 | 29520 | 8336 | 1621 | 39282 | 33516 | 1006 |
| 24 | 48370 | 8657 | 9882 | 19107 | 15197 | 2232 |
| 25 | 75650 | 17815 | 1235 | 18184 | 28310 | 2810 |
| 26 | 31430 | 1526 | 8882 | 62741 | 40355 | 1277 |
| 27 | 256050 | 9250 | 4813 | 20705 | 39373 | 1085 |
| 28 | 86830 | 6545 | 1653 | 72342 | 15002 | 6701 |
| 29 | 50002 | 4908 | 4589 | 14546 | 47844 | 1202 |
| 30 | 38654 | 3016 | 1579 | 22661 | 27833 | 7555 |
| 31 | 83761 | 20950 | 1570 | 23480 | 17210 | 4393 |
| 32 | 61235 | 27133 | 1321 | 25590 | 19700 | 4400 |
| 33 | 55320 | 11500 | 1754 | 18650 | 20600 | 3650 |
Распределение варианта заданий 1и 2.
| Номер варианта | Номер предприятий | Результативный признак | Группировочный признак |
| 4 | 4-33 | Прибыль от продаж | Основные средства |
Построим дискретный ряд по группировочному признаку, в нашем случае группировочный признак основные средства:
Таблица 2. - Дискретный ряд
| № п/п | Прибыль от продаж, т.р. | Основные средства, т.р. |
| 4 | 24774 | 106447 |
| 5 | 9210 | 92805 |
| 6 | 4678 | 52187 |
| 7 | 13115 | 46234 |
| 8 | 4809 | 56932 |
| 9 | 2381 | 47067 |
| 10 | 65920 | 54356 |
| 11 | 7659 | 29351 |
| 12 | 4817 | 62651 |
| 13 | 1089 | 40633 |
| 14 | 20995 | 64567 |
| 15 | 5515 | 58711 |
| 16 | 10786 | 87210 |
| 17 | 3412 | 57195 |
| 18 | 2014 | 33465 |
| 19 | 7469 | 32176 |
| 20 | 38983 | 11553 |
| 21 | 2586 | 40150 |
| 22 | 6310 | 13488 |
| 23 | 8336 | 39282 |
| 24 | 8657 | 19107 |
| 25 | 17815 | 18184 |
| 26 | 1526 | 62741 |
| 27 | 9250 | 20705 |
| 28 | 6545 | 72342 |
| 29 | 4908 | 14546 |
| 30 | 3016 | 22661 |
| 31 | 20950 | 23480 |
| 32 | 27133 | 25590 |
| 33 | 11500 | 18650 |
Величина интервала группировки определяется по формуле:
![]() ,
,
где d – величина интервала, k – число групп, R – размах вариации, xmax- максимальное значение группировочного признака в совокупности, xmin- минимальное значение группировочного признака.
xmax=106447; xmin=11553
![]() =23723,5
=23723,5
В результате подсчета предприятий в каждой группе получим ряд распределения предприятий по размеру основных средств. Минимальное значение признака совпадает с верхней границей первой группы, а максимальное значение признака совпадает с нижней границей четвертой группы. Рассчитаем показатели центра распределения: x, Мо, Ме. Среднюю величину в интервальном ряду распределения определим по формуле средней арифметической взвешенной:
 ,
,
Х – Средняя величина; x'i – среднее значение признака в интервале (центр интервала), fi – число единиц совокупности в интервале (частота).
X=![]() =44762,9
=44762,9
Результаты группировки предприятий по размеру основных средств:
| Группа п/п по размеру основных средств, xi | Число предприятий ,fi | Середина интервала, x'i | x'i×fi | Накопленная частота, Si |
| 11553 - 35276,5 | 13 | 23414,75 | 304391,75 | 13 |
| 35276,5 – 59000 | 10 | 47138,25 | 471382,5 | 23 |
| 59000 – 82723,5 | 4 | 70861,75 | 283447 | 27 |
| 82723,5 – 106447 | 3 | 94585,25 | 283755,75 | 30 |
| 30 | 1342977 |
Мода – наиболее часто встречающееся значение признака в совокупности. Для определения величины моды используют следующую формулу:
Мо= xМо+d![]() ,
,
где xМо – начало модального интервала; fМо – частота, соответствующая модальному интервалу; fМо-1 – предмодальная; fМо+1 – послемодальная.
Мо=11553+23723,5![]() =11553+23723,5
=11553+23723,5![]() =30828,34
=30828,34
Для определения величины медианы используем следующую формулу:
Ме=xМе+d(![]() -SМе-1)/fМе,
-SМе-1)/fМе,
где xМе – нижняя граница медианного интервала; SМе-1 – накопленная частота интервала, предшествующая медианному; fМе- частота медианного интервала.
Ме=11553+23723,5![]() =38926,27
=38926,27
Выяснение общего характера распределения включает также оценку степени однородности, а также вычисление показателей ассиметрии (Аs) и эксцесса (Еs). Простейший показатель ассиметрии основан на соотношении показателей центра распределения: чем больше разница между средними (x-Мо), тем больше ассиметрия ряда. В нашем случае 44762,9 – 30828,34 =13937,56.
Величина показателя ассиметрии в нашем примере положительная , что указывает на наличие правосторонней ассиметриии (Мо<Ме<x): 30828,34<38926,27<44762,9.
Задание 2. Для выявления зависимости между экономическими показателями деятельности предприятий провести аналитическую группировку показателей 30 предприятий. Группировку провести с равными интервалами, выделив четыре группы. Рассчитать коэффициенты вариации по группировочному признаку на основании исходных данных и по аналитической группировке согласно своего варианта. Объяснить расхождения в значениях полученных коэффициентов.
Таблица 3. - Распределим предприятия по величине основных средств.
| № п/п | Основные средства, т.р. | № п/п | Основные средства, т.р. |
| 4 | 106447 | 19 | 32176 |
| 5 | 92805 | 20 | 11553 |
| 6 | 52187 | 21 | 40150 |
| 7 | 46234 | 22 | 13488 |
| 8 | 56932 | 23 | 39282 |
| 9 | 47067 | 24 | 19107 |
| 10 | 54356 | 25 | 18184 |
| 11 | 29351 | 26 | 62741 |
| 12 | 62651 | 27 | 20705 |
| 13 | 40633 | 28 | 72342 |
| 14 | 64567 | 29 | 14546 |
| 15 | 58711 | 30 | 22661 |
| 16 | 87210 | 31 | 23480 |
| 17 | 57195 | 32 | 25590 |
| 18 | 33465 | 33 | 18650 |
Величина интервала группировки определяется по формуле:
![]() ,
,
где d – величина интервала, k – число групп, R – размах вариации, xmax- максимальное значение группировочного признака в совокупности, xmin- минимальное значение группировочного признака.
xmax=106447; xmin=11553
![]() =23723,5
=23723,5
В результате подсчета предприятий в каждой группе получим ряд распределения предприятий по размеру основных средств. Минимальное значение признака совпадает с верхней границей первой группы, а максимальное значение признака совпадает с нижней границей четвертой группы.
Таблица 1- Распределение предприятий по размеру основных средств
| Номер группы | Граница | |
| нижняя | верхняя | |
| 1 | 11553 | 35276,5 |
| 2 | 35276,5 | 59000 |
| 3 | 59000 | 82723,5 |
| 4 | 82723,5 | 106447 |
Таблица 2Группировка предприятий по величине основных средств.
| Группы предприятий по величине основных средств, тыс.руб | Число предприятий в группе | Предприятие | Всего по группе, тыс.руб | Средний размер основных средств по группе, тыс.руб. |
| 11553 - 35276,5 | 13 | 11,18,19,20,22,24,25,27,29,30,31,32,33 | 282956 | 21765,85 |
| 35276,5 – 59000 | 10 | 6,7,8,9,10,13,15,17,21,23 | 492747 | 49274,7 |
| 59000 – 82723,5 | 4 | 12,14,26,28 | 262301 | 65575,25 |
| 82723,5 – 106447 | 3 | 4,5,16 | 286462 | 95487,33 |
| Итого | 30 | 1324466 | 44148,87 |
Таблица 3. - Расчет показателей вариации для предприятий, сгруппированных по величине основных средств.
| Группы предприятий по величине основных средств, млн.руб | Число п/п fi | Расчетные показатели | |||
| xi' | xi' fi | xi'-x | (xi'-x)2 fi | ||
| 11,5 – 35,3 | 13 | 23,4 | 304,2 | -21,34 | 5920,14 |
| 35,2 – 59,0 | 10 | 47,1 | 471,0 | 2,36 | 55,69 |
| 59,0 – 82,7 | 4 | 70,8 | 283,4 | 26,06 | 2716,5 |
| 82,7 – 106,4 | 3 | 94,6 | 283,7 | 49,86 | 7458,05 |
| Итого | 30 | 1342,3 | 16150,38 | ||
Рассчитаем коэффициенты вариации для исходным данным и по аналитической таблице. Среднее по исходным данным:
X=![]() =
=![]() =44,15 млн. руб.
=44,15 млн. руб.
По сгруппированным данным:
X=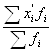 =
=![]() =44,74 млн. руб.
=44,74 млн. руб.
Среднее квадратичное по исходным данным:
σ=![]() =37,53 млн. руб.
=37,53 млн. руб. ![]()
Среднее квадратичное отклонение по сгруппированным данным:
σ=![]() =23,20 млн. руб.
=23,20 млн. руб.
Находим коэффициент вариации по формуле:
ν=![]()
Коэффициент вариации по исходным данным:
ν=![]() *100%=85%
*100%=85%
Коэффициент вариации по сгруппированным данным:
ν=![]() =51,86%
=51,86%
В обоих расчетах коэффициент вариации значительно больше 33%. Следовательно, рассмотренная совокупность неоднородна и средняя для нее недостаточна типична.
Задание 3. Выполнить анализ показателей бухгалтерского баланса (Форма 1) путем расчета показателей структуры и динамики. Данные для выполнения задания взяты по ООО торговый дом «Светлый» на 30.07.2008г. По результатам расчетов охарактеризовать основные тенденции изменения структуры в динамике. Для выполнения аналитических исследований и оценок структуры актива и пассива баланса произвести группировку его статей.
Таблица 4 – Статьи баланса
| Статьи баланса | Базисный период | Отчетный период | Отклонения | Динамика отчетного периода в % к базисному | |||
| Сумма, тыс.руб. | Удельный вес, % | Сумма, тыс.руб. | Удельный вес, % | В сумме, тыс.руб. | В процентах, % | ||
| А | 1 | 2 | 3 | 4 | 5=3-1 | 6=4-2 | 7=3/1*100% |
| Внеоборотные активы | 554 | 8,8 | 496 | 8,5 | -58 | -0,3 | 89,5 |
| Оборотные активы | 5732 | 91,2 | 5346 | 91,5 | -386 | -0,3 | 93,3 |
| Баланс | 6286 | 100,0 | 5842 | 100,0 | |||
| Капитал и резервы | 2969 | 47,2 | 3444 | 59,0 | 475 | 11,8 | 116,0 |
| Долгосрочные обязательства | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Краткосрочные обязательства | 3317 | 52,8 | 2398 | 41,0 | -919 | -11,8 | 72,3 |
| Баланс | 6286 | 100,0 | 5842 | 100,0 | |||
Для характеристики интенсивности изменения во времени к таким показателям относят:
Абсолютный прирост;
Темп прироста;
Темп роста;
Коэффициент роста.
Когда сравнение проводится с периодом (моментом) времени, начальным в ряду динамики, получают базисные показатели; при сравнении же с предыдущим периодом или моментом времени речь идет о цепных показателях.
Задание 4.Провести 25% механическую выборку из генеральной совокупности по показателю, который является для нас результативным. С вероятностью 0,954 рассчитать границы изменения средней величины в генеральной совокупности и сравнить с результатом, полученным на основании расчета по выборочной совокупности. Начало отбора начинать с номера предприятия совпадающего с номером варианта. Сформулировать вывод.
Выборочный метод применяется в тех случаях, когда проведение наблюдения невозможно или экономически нецелесообразно.
Часть единиц, отобранных для наблюдения, принято называть выборочной совокупностью, а всю совокупность единиц, из которых производится отбор, - генеральной. Качество результатов выборочного наблюдения зависит от того, насколько состав выборки представляет совокупность.
По заданию следует начать с номера предприятия, совпадающего с номером варианта. При 33% выборке шаг отсчета (1/0,33) равен 3.
| Номер предприятия | Основные средства, млн. руб. | Расчетные показатели | |
| x-x | (x-x)2 | ||
| 4 | 106,45 | 57,0 | 3249 |
| 7 | 46,23 | -3,22 | 10,36 |
| 10 | 54,36 | 4,91 | 24,11 |
| 13 | 40,63 | -8,82 | 77,79 |
| 16 | 87,21 | 37,76 | 1425,82 |
| 19 | 32,18 | -17,27 | 298,25 |
| 22 | 13,49 | -35,96 | 1293,12 |
| 25 | 18,18 | -31,27 | 977,81 |
| 28 | 72,34 | 22,89 | 523,95 |
| 31 | 23,48 | -25,97 | 674,44 |
| Итого | 494,55 | 8554,65 | |
Величина средней ошибки механического бесповторного отбора для малых выборок определяется по упрощенной формуле:
µx = ![]() ,
,
где N – объем генеральной совокупности (число входящих в нее единиц), n=10 – объем выборки (число обследованных единиц), S2 – выборочная дисперсия (дисперсия признака в выборочной совокупности).
Наиболее часто употребляемые уровни доверительной вероятности и соответствующие значения отношения Стьюдента (коэффициента доверия) t при числе степеней свободы k=n – 1 = 9:
| P | 0,9 | 0,95 | 0,98 | 0,99 | 0,999 |
| t | 1,740 | 2,110 | 2,567 | 2,898 | 3,965 |
Для расчета границ изменения средней характеристики генеральной совокупности по материалам выборки воспользуемся следующими формулами:
x= x±∆
∆ = t µx
(x – средняя выборочной совокупности;
x – средняя генеральной совокупности;
∆ - предельная ошибка выборки;
µx – средняя ошибка выборки).
Средняя стоимость основных средств на одном предприятии по выборочной совокупности равна:
x = ![]() млн. руб.
млн. руб.
дисперсия S2 =855,47; t = 3,965; n/N = 0,33, т.к. процент отбора составляет 33%.
µx =![]()
Рассчитаем предельную ошибку и определим границы изменения средней:
∆= 3,965 *7,98=31,64
49,45 - 31,64 <x<49,45+31,64
17,81<x<81,09
Таким образом, с вероятностью 0,999 можно утверждать, что стоимость основных средств на одном предприятии в генеральной совокупности будет находиться в пределах от 17,81 млн. руб. до 81,09 млн. руб.
Задание 5. По данным своего варианта исчислить: Базисные, цепные и среднегодовые показатели абсолютного прироста, темпов роста и темпов прироста объемов индивидуального жилищного строительства.
Среднегодовой объем индивидуального жилищного строительства.
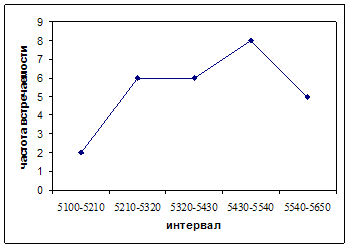
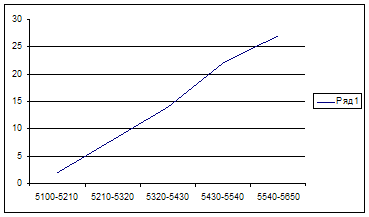
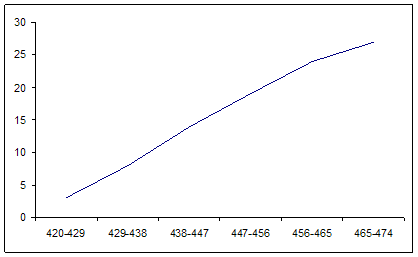
Изобразить динамику индивидуального жилищного строительства на графике.
Таблица 5 - Данные об объеме индивидуального жилищного строительства по району
| Период в годах, год | Объем индивидуального жилищного строительства, м2 общей площади |
| 1989 | 234 |
| 1990 | 240 |
| 1991 | 242 |
| 1992 | 258 |
| 1993 | 267 |
| 1994 | 457 |
| 1995 | 480 |
| 1996 | 632 |
| 1997 | 718 |
| 1998 | 1319 |
Динамический ряд представляет собой ряд последовательных уровней, сопоставляя которые между собой можно получить характеристику скорости и интенсивности развития явления. В результате сравнения уровней получается система абсолютных и относительных показателей динамики, к числу которых относятся абсолютный прирост, темп роста, темп прирос та, абсолютное значение одного процента прироста и пункты роста.
Абсолютный прирост (∆i ) определяется как разность между двумя уровнями динамического ряда. При сравнении с постоянной базой он равен:
∆i баз= Yi – Y0
где∆i баз - абсолютный прирост базисный; У1 - уровень сравниваемого периода; У0 - уровень базисного периода.
При сравнении с переменной базой
∆i = Yi – Yi-1
Где ∆i - абсолютный прирост цепной; Yi-1 - уровень непосредственно предшествующего периода. Темп роста определяется как отношение двух сравниваемых уровней. Пои сравнения с постоянной базой
Тр= (Yi : Y0) * 100
При сравнении с переменной базой
Тр= (Yi : Yi-1) * 100
Темп прироста показывает на сколько процентов уровень данного пе риода больше (или меньше) базисного уровня.
Тпр= ![]() или Тпр =
или Тпр = ![]()
а также как разность между темпом роста (в процентах) и 100%
Тпр = Тр – 100%
Рассчитаем все показатели по ряду динамики, характеризующему объем индивидуального жилищного строительства. Данные расчета представить в таблице:
Таблица 6 - Показатели по ряду динамики
| Год | Общая площадь, м2 | Абсолютный прирост (∆) | Темп роста, % (Тр) | Темп прироста, % (Тпр) | |||
| цепной | базисный | цепной | базисный | цепной | базисный | ||
| 1989 | 234 | - | 0,0 | - | 100 | 0,0 | 0,0 |
| 1990 | 240 | 6 | 6 | 102 | 102 | 2 | 2 |
| 1991 | 242 | 2 | 8 | 101 | 103 | 1 | 3 |
| 1992 | 258 | 16 | 24 | 106 | 110 | 6 | 10 |
| 1993 | 267 | 9 | 33 | 103 | 114 | 3 | 14 |
| 1994 | 457 | 190 | 223 | 171 | 195 | 71 | 95 |
| 1995 | 480 | 23 | 246 | 105 | 205 | 5 | 105 |
| 1996 | 632 | 152 | 398 | 132 | 270 | 32 | 170 |
| 1997 | 718 | 86 | 484 | 114 | 307 | 14 | 207 |
| 1998 | 1319 | 601 | 1085 | 184 | 564 | 84 | 464 |
Рассчитаем средние показатели:
а) средний уровень: Y= 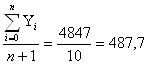 м2
м2
б) средний абсолютный прирост:
∆=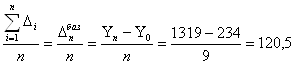 м2
м2
в) среднегодовой темп роста по формуле среднегеометрической:
Тр=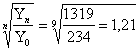
Рассчитанные аналитические показатели характеризуют состояние объема индивидуального жилищного строительства за 1989 – 1998 годы. Абсолютный прирост показывает скорость увеличения объемов строительства по сравнению с 1989 годом он составил 1085 м2. Темп роста показывает, что объем строительства 1998 года составил 564% от уровня базисного года (1989). Темп прироста дает возможность оценить на сколько процентов объем строительства в 1998 увеличился по сравнению с 1989 – 464%.
Задание 6. По данным своего варианта определить:
Общие индексы:
а) цен;
б) физические объемы проданных товаров,
в) товарооборота.
Какую роль в изменении товарооборота сыграли изменения цен и количества проданных товаров?
Абсолютную величину изменения расходов населения в связи с изменением цен.
Таблица 7 - Реализация товаров в магазине
| Вид товара | Предыдущий период | Отчетный период | ||
| Кол-во, шт. | Цена за единицу, руб. | Кол-во, шт. | Цена за единицу, руб. | |
| Ноутбук Монитор | 10 8 | 6500 3200 | 14 12 | 5500 3400 |
Общий индекс цен рассчитываем по формуле:
Jp = 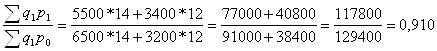
Цены на оба товара снизились в среднем на 9%
Общий индекс физического объема товарооборота (количество проданного товара) находим по формуле:
Jq = 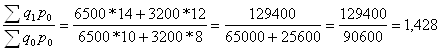
Количество проданного товара отчетном периоде было продано больше на 42,8%, чем в предыдущем.
Теперь рассчитаем общий индекс товарооборота:
Jpq = 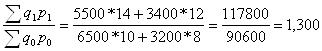
Товарооборот увеличился в отчетном периоде на 30% по сравнению с предыдущим периодом.
Увеличение товарооборота произошло за счет уменьшения цены:
∑p1q1 - ∑p0q1=117800 – 129400 = - 11600 руб.
В тоже время увеличение товарооборота произошло за счет изменения количества проданного товара:
∑p0q1 - ∑p0q0 = 129400 – 90600 = 38800руб.
Следовательно, увеличение товарооборота на 11600 руб. произошло за счет увеличения проданных товаров на 38800 руб. и за счет уменьшения роста цен на 27200 (38800 + (-11600) = 27200 руб.).
Задание 7. Для выявления зависимости между группировочным и результативным показателями рассчитать линейный коэффициент корреляции по исходным данным.
| № п/п | Основные средства, млн.руб. (группировочный признак) (x) | Выручка от продажи товаров, млн.руб. (результативный признак) (y) | xy | x2 | y2 |
| 4 | 106 | 344 | 36464 | 11236 | 118336 |
| 5 | 93 | 107 | 9951 | 8649 | 11449 |
| 6 | 52 | 105 | 5460 | 2704 | 11025 |
| 7 | 46 | 198 | 9108 | 2116 | 39204 |
| 8 | 57 | 85 | 4845 | 3249 | 7225 |
| 9 | 47 | 62 | 2914 | 2209 | 3844 |
| 10 | 54 | 171 | 9234 | 2916 | 29241 |
| 11 | 29 | 45 | 1305 | 841 | 2025 |
| 12 | 63 | 110 | 6930 | 3969 | 12100 |
| 13 | 41 | 32 | 1312 | 1681 | 1024 |
| 14 | 64 | 71 | 4544 | 4096 | 5041 |
| 15 | 59 | 21 | 1239 | 3481 | 441 |
| 16 | 87 | 24 | 2088 | 7569 | 576 |
| 17 | 57 | 56 | 3192 | 3249 | 3136 |
| 18 | 33 | 56 | 1848 | 1089 | 3136 |
| 19 | 32 | 45 | 1440 | 1024 | 2025 |
| 20 | 11 | 183 | 2013 | 121 | 33489 |
| 21 | 40 | 21 | 840 | 1600 | 441 |
| 22 | 13 | 24 | 312 | 169 | 576 |
| 23 | 39 | 29 | 1131 | 1521 | 841 |
| 24 | 19 | 48 | 912 | 361 | 2304 |
| 25 | 18 | 75 | 1350 | 324 | 5625 |
| 26 | 63 | 31 | 1953 | 3969 | 961 |
| 27 | 20 | 256 | 5120 | 400 | 65536 |
| 28 | 72 | 86 | 6192 | 5184 | 7396 |
| 29 | 14 | 50 | 700 | 196 | 2500 |
| 30 | 22 | 38 | 836 | 484 | 1444 |
| 31 | 23 | 83 | 1909 | 529 | 6889 |
| 32 | 25 | 61 | 1525 | 625 | 3721 |
| 33 | 18 | 55 | 990 | 324 | 3025 |
| Итого | 1317 | 2572 | 127657 | 75885 | 384576 |
По данным о стоимости основных фондов и выручке от продаж товара необходимо оценить тесноту связи.
Расчеты парного коэффициента корреляции следует произвести по следующей формуле:
r = 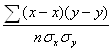
или
r = ![]()
где x, y – индивидуальные значения факторного и результативного признаков; x, y – средние значения признаков; xy – средняя из произведений индивидуальных значений признаков; σx, σy – средние квадратические отклонения признаков.
Рассчитаем величину линейного коэффициента корреляции:
r = 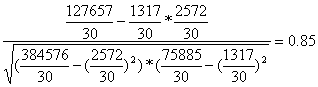
Коэффициент парной корреляции близок к единице, можно говорить о тесной связи изучаемых признаков.
Список используемой литературы
1. Елисеева, И.И. Общая теория статистики: Учебник для вузов / И.И. Елисеева, М.М. Юзбашев. - 5-е изд. Пер. и доп. - М.: Финансы и статистика, 2004. - 656 с.
2. Ефимова, М.Р. Общая теория статистики / М.Р. Ефимова, Е.В. Петрова, В.Н. Румянцев. - М.: ИНФРА-М, 1997.-416 с.
3. Ефимова, М.Р. Практикум по общей теории статистики : Учеб. пособие / М.Р. Ефимова, О.И. Ганченко, Е.В. Петрова. - М.: Финансы и статистика, 1999. -280 с.
4. Общая теория статистики. Статистическая методология в изучении коммерческой деятельности / Под ред. О.Э. Башиной и А.А. Спирина. - М.: Финансы и статистика, 2001. -440 с.
5. Сборник задач по общей теории статистики. Учеб. пособие / Под ред. к.э.н. Л.К. Серпа.- - М.: Инф.- изд. дом Филинъ, 1999. - 360 с.
6. Статистика: Учебное пособие / Под ред. В.Г. Ионина. - 2-е изд. пер и доп. - М.: ИНФРА-М, 2002. - 384 с.
7. Статистика: Учеб. пособие / Под ред. М.Р. Ефимовой. -М.: ИНФРА-М, 2002. - 336 с.
8. Сборник задач по теории статистики / Под ред. В.В. Глинского - М ' ИНФРА-М, 2002. - 257 с.
9. Теория статистики: Учеб для вузов / Под ред. Р.А. Шмойловой. - 3-е изд. перер. - М.: Финансы и статистика, 2002. - 560 с.
Похожие работы
... , табличные характеристики связи. Это в свою очередь потребовало решения соответственно теоретико-методологических проблем. Глава 2. Абсолютные и относительные величины 2.1. Понятие, формы выражения и виды статистических показателей Статистическое исследование независимо от его масштабов и целей всегда завершается расчетом и анализом различных по виду и форме выражения статистических ...
... по их запросам статистическая информация предоставляется на платной основе. Статистической информации с ограниченным доступом предоставляется пользователям в соответствии с законодательством Российской Федерации. 2. Формирование единого информационного пространства В процессе осуществления статистического учета Федеральные органы исполнительной власти и их территориальные органы ...
... : х - стаж по специальности; f - накопленная частота. Графики являются важным средством выражения и анализа статистических данных, поскольку наглядное представление облегчает восприятие информации. Графики позволяют мгновенно охватить и осмыслить совокупность показателей - выявить наиболее типичные соотношения и связи этих показателей, определить тенденции развития охарактеризовать структуру и ...
... наблюдения – можно ли распространить результаты выборочной совокупности на генеральную совокупность или нет, следовательно, проверка выборочной совокупности на точность это необходимая часть анализа при несплошном наблюдении. Существуют два вида оценок статистических показателей на точность: точечная и интервальная. Точечная представляет собой оценку параметра в генеральной совокупности одним чи
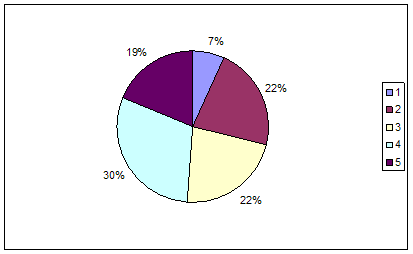
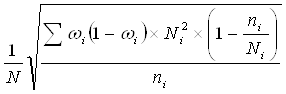
0 комментариев