Задача 1.
Плановое задание по реализации продукции на 2000г. составляет 108% показатель динамики за 2000г. по сравнению с 1979г. - 113,4%. На сколько процентов выполнен план по реализации продукции в 2000г.
Решение:
Плановое задание по реализации продукции на 2000г.:
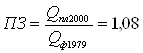 ,
,
значит ![]()
Показатель динамики за 2000г. по сравнению с 1979г.:
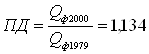 , значит
, значит ![]()
Вычислим процент выполнения плана по реализации продукции в 2000г.:
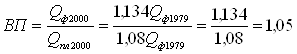 , или 105%
, или 105%
Значит план по реализации продукции в 2000г. перевыполнили на 5%.
Задача 2.
Численность населения и число построенных квартир в двух районах характеризуются следующими данными:
| Район | Число построенных квартир, тыс. шт. | Численность населения, млн. чел. | ||
| 1990г. | 2000г. | 1990г. | 2000г. | |
| А Б | 107 208 | 233 180 | 18 15 | 25 21 |
Вычислите все возможные относительные величины. Укажите к какому виду они относятся. За базу сравнения примите уровень Б.
Решение:
Динамика числа построенных квартир:
- район А 233 / 107 = 2,178 или 217,8%
- район Б 180 / 208 = 0,865 или 86,5%.
Динамика численности населения:
- район А 25 / 18 = 1,389 или 138,9%
- район Б 21 / 15 = 1,4 или 140%.
Коэффициент координации числа построенных квартир в районе А к району Б:
- 1990г. 107 / 208 = 0,514 или 51,4%
- 2000г. 233 / 180 = 1,294 или 129,4%
Коэффициент координации численности населения в районе А к району Б:
- 1990г. 18 / 15 = 1,2 или 120%
- 2000г. 25 / 21 = 1,190 или 119%
Задача 3.
План роста производительности труда на 1999г. выполнен предприятием на 102%, показатель динамики производительности труда за 1999г. по сравнению с 1998г. – 107,1%. Определите плановое задание по росту производительности труда на 1999г.
Решение:
План роста производительности труда на 1999г.:
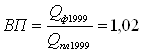 , значит
, значит ![]()
Показатель динамики производительности труда за 1999г. по сравнению с 1998г.:
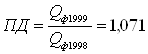 , значит
, значит ![]()
Плановое задание по росту производительности труда на 1999г.:
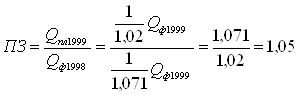 или 105%
или 105%
Значит плановое задание по росту производительности труда на 1999г. составило 105%.
Задача 4.
| Группы предприятий по размеру основных фондов, млн. руб. | 1 - 3 | 3 - 5 | 5 - 7 | 7 - 9 | Более 9 |
| Число предприятий в % к итогу | 15 | 30 | 20 | 25 | 10 |
Найти средний размер основных фондов, моду и медиану, дисперсию, среднее линейное и среднее квадратическое отклонение, коэффициент вариации.
Решение:
Построим вспомогательную таблицу:
| Группы предприятий по размеру основных фондов, млн. руб. | Середина интервала, хi | Число предприятий в % к итогу, fi | хi fi |
| ( |
| 1 – 3 | 2 | 15 | 30 | 55,5 | 205,35 |
| 3 – 5 | 4 | 30 | 120 | 51 | 86,7 |
| 5 – 7 | 6 | 20 | 120 | 6 | 1,8 |
| 7 – 9 | 8 | 25 | 200 | 57,5 | 132,25 |
| Более 9 | 10 | 10 | 100 | 43 | 184,9 |
| Итого: | - | 100 | 570 | 213 | 611 |
Средний размер основных фондов
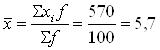 (млн. руб.)
(млн. руб.)
Мода размера основных фондов:
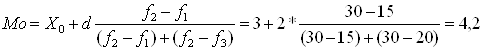 (млн. руб.)
(млн. руб.)
Значит большинство предприятий имеет размер основных фондов 4,2 млн. руб.
Медиана размера основных фондов:
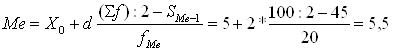 (млн. руб.)
(млн. руб.)
Значит 50% предприятий имеют размер основных фондов менее 5,5 млн. руб., а 50% - более 5,5 млн. руб.
Среднее линейное отклонение размера основных фондов:
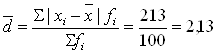 (млн. руб.)
(млн. руб.)
Среднее квадратическое отклонение размера основных фондов:
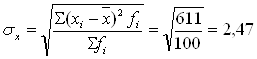 (млн. руб.)
(млн. руб.)
Коэффициент вариации:
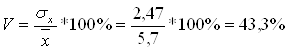 > 33%,
> 33%,
значит совокупность предприятий по размеру основных фондов считать однородной нельзя.
Задача 5
| Группы рабочих по возрасту, лет | Число рабочих, чел. |
| 18 – 20 | 5 |
| 20 – 22 | 10 |
| 22 – 24 | 20 |
| Более 24 | 5 |
Найти средний возраст одного рабочего, моду медиану и коэффициент вариации.
Решение:
Построим вспомогательную таблицу:
| Группы рабочих по возрасту, лет | Середина интервала, хi | Число рабочих, fi | хi fi |
| ( |
| 18 – 20 | 19 | 5 | 95 | 16,25 | 52,8125 |
| 20 – 22 | 21 | 10 | 210 | 12,5 | 15,625 |
| 22 – 24 | 23 | 20 | 460 | 15 | 11,25 |
| Более 24 | 25 | 5 | 125 | 13,75 | 37,8125 |
| Итого: | - | 40 | 890 | 57,5 | 117,5 |
Средний возраст одного рабочего
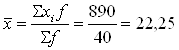 (лет)
(лет)
Мода возраста одного рабочего:
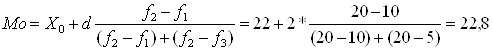 (лет)
(лет)
Значит возраст большинства рабочих составляет 22,8 лет.
Медиана возраста одного рабочего:
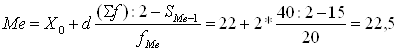 ( лет)
( лет)
Значит возраст 50% рабочих менее 22,5 лет, а других 50% - более 22,5 лет.
Среднее линейное возраста одного рабочего:
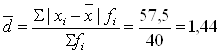 (лет)
(лет)
Среднее квадратическое отклонение возраста одного рабочего:
 (лет)
(лет)
Коэффициент вариации:
![]() < 33%,
< 33%,
значит совокупность рабочих по возрасту можно считать однородной.
Задача 6
| Группы рабочих по размеру зарплаты, руб. | Число рабочих, чел. |
| 800 – 1200 | 10 |
| 1200 – 1600 | 20 |
| 1600 – 2000 | 10 |
| Более 2000 | 5 |
Определить моду и коэффициент асимметрии.
Решение:
Мода заработной платы одного рабочего:
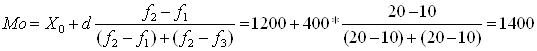 (руб.)
(руб.)
Значит зарплата большинства рабочих составляет 1400 руб.
| Группы рабочих по размеру зарплаты, руб. | Середина интервала, хi | Число рабочих, fi | хi fi | Накопленная частота |
| 800 – 1200 | 1000 | 10 | 10000 | 10 |
| 1200 – 1600 | 1400 | 20 | 28000 | 30 |
| 1600 – 2000 | 1800 | 10 | 18000 | 40 |
| Более 2000 | 2200 | 5 | 11000 | 45 |
| Итого: | - | 45 | 67300 | - |
Средний размер заработной платы одного рабочего
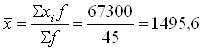 (руб.)
(руб.)
Медиана возраста одного рабочего:
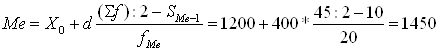 (руб.)
(руб.)
Если M0 < Me <![]() имеет место правосторонняя асимметрия, если же
имеет место правосторонняя асимметрия, если же ![]() < Me <M0 - левосторонняя асимметрия ряда. По приведенному примеру можно сделать заключение, что асимметрия – правосторонняя.
< Me <M0 - левосторонняя асимметрия ряда. По приведенному примеру можно сделать заключение, что асимметрия – правосторонняя.
Задача 7
| Группы студентов по возрасту, лет | Число студентов, чел. |
| 18 – 20 | 5 |
| 20 – 22 | 10 |
| 22 – 24 | 20 |
| Более 24 | 5 |
Найти средний возраст одного студента, используя метод моментов, среднеквадратическое отклонение и коэффициент вариации.
Решение:
Построим вспомогательную таблицу:
| Группы рабочих по возрасту, лет | Середина интервала, хi | Условная варианта аi | Число рабочих, fi | аi fi | аi2fi |
| 18 – 20 | 19 | -2 | 5 | -10 | 20 |
| 20 – 22 | 21 | -1 | 10 | -10 | 10 |
| 22 – 24 | 23 | 0 | 20 | 0 | 0 |
| Более 24 | 25 | 1 | 5 | 5 | 5 |
| Итого: | - | - | 40 | -15 | 35 |
Найдем средний возраст студентов:
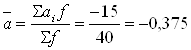
Тогда
![]() (лет)
(лет)
Найдем среднее квадратическое отклонение:
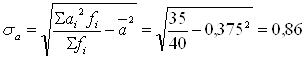
Тогда
![]() (лет)
(лет)
Коэффициент вариации:
![]() < 33%,
< 33%,
значит совокупность студентов по возрасту можно считать однородной.
Задача 8.
Имеются данные о среднегодовой стоимости ОФ двух пароходств АО»Волга-флот» и Ленское объединение речное пароходство.
| Ао «Волга-флот№» | АО «ЛОРП» | ||
| Группы предприятий по среднегодовой стоимости ОПФ, млн. руб. | Количество предприятий в % к итогу | Группы предприятий по среднегодовой стоимости ОПФ, млн. руб. | Количество предприятий в % к итогу |
| До 200 | 2 | До 200 | 1 |
| 200 – 220 | 12 | 200 – 250 | 27 |
| 220 – 240 | 24 | 250 – 300 | 36 |
| 240 – 260 | 22 | 300 – 350 | 38 |
| 260 – 280 | 18 | Свыше 350 | 8 |
| 280 – 300 | 9 | ||
| 300 – 320 | 11 | ||
| 320 – 340 | 10 | ||
| Свыше 340 | 2 | ||
| Итого: | 110 | 110 | |
1. Проведите вторичную группировку предприятий АО «Волга-флот» по среднегодовой стоимости ОПФ (по величине интервала АО «ЛОРП»).
2. Рассчитайте среднегодовую стоимость ОПФ АО «Волга-флот» и АО «ЛОРП».
3. Выполните сравнительный анализ полученных результатов по двум пароходствам.
Решение:
1. Проведением вторичную группировку предприятий АО «Волга-флот» по среднегодовой стоимости ОПФ (по величине интервала АО «ЛОРП»).
| Ао «Волга-флот№» | |
| Группы предприятий по среднегодовой стоимости ОПФ, млн. руб. | Количество предприятий в % к итогу |
| До 200 | 2 |
| 200 – 250 | 47 |
| 250 – 300 | 38 |
| 300 – 350 | 22 |
| Свыше 350 | 1 |
2. Рассчитаем среднегодовую стоимость ОПФ АО «Волга-флот»:
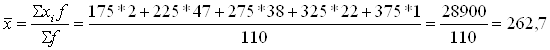
(млн. руб.)
Рассчитаем среднегодовую стоимость АО «ЛОРП».
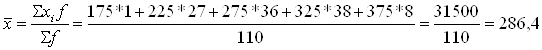
(млн. руб.)
3. Видим, что среднегодовая стоимость основных производственных фондов на АО «ЛОРП» превышает среднегодовую стоимость основных фондов на АО «Волга-флот» на 23,7 млн. руб.
Задача 9
Объем реализованной продукции предприятий составил, млн. руб.:
4,0 3,0 8,4 4,8 0,9 1,4 3,0 4,0 1,8 3,0
Требуется:
1. Произвести группировку предприятий по объему реализованной продукции;
2. Составить дискретный ряд;
3. Изобразить ряд графически;
4. Определить накопленные частоты.
Решение:
1. Произведем группировку предприятий по объему реализованной продукции и составим дискретный ряд:
| Объем реализованной продукции, млн. руб. | 0,9 | 1,4 | 1,8 | 3,0 | 4,0 | 4,8 | 8,4 | Итого: |
| Число предприятий | 1 | 1 | 1 | 3 | 2 | 1 | 1 | 10 |
2. Изобразим полученный ряд графически:
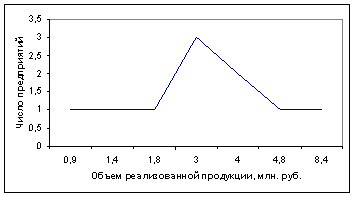
3. Определим накопленные частоты:
| Объем реализованной продукции, млн. руб. | 0,9 | 1,4 | 1,8 | 3,0 | 4,0 | 4,8 | 8,4 |
| Накопленные частоты | 1 | 2 | 3 | 6 | 8 | 9 | 10 |
4. Определим средний объем реализованной продукции:
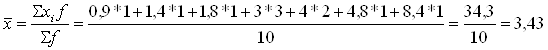
(млн. руб.)
Задача 10.
Объем валовой продукции предприятий составил, млн. руб.:
4,0 3,0 8,4 4,8 0,9 1,4 3,0 4,0 1,8 3,0
Требуется:
1. Произвести группировку предприятий по объему валовой продукции;
2. Составить интервальный ряд распределения;
3. Изобразить ряд графически;
4. Определить накопленные частоты.
Решение:
1. Произведем группировку предприятий по объему валовой продукции и составим интервальный ряд распределения:
| Объем валовой продукции, млн. руб. | 0,9 – 3,4 | 3,4 – 5,9 | 5,9 – 8,4 | Итого: |
| Число предприятий | 6 | 3 | 1 | 10 |
2. Изобразим полученный ряд графически:
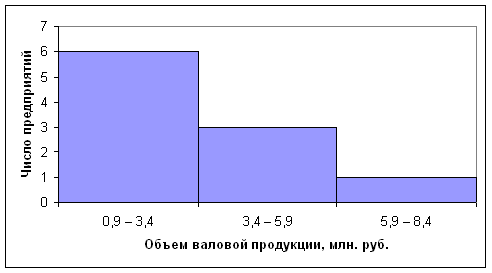
4. Определим накопленные частоты:
| Объем валовой продукции, млн. руб. | 0,9 – 3,4 | 3,4 – 5,9 | 5,9 – 8,4 |
| Накопленные частоты | 6 | 9 | 10 |
Задача 11.
По данным таблицы определить средний годовой темп роста объема перевезенных грузов речным транспортом, абсолютный прирост, темпы роста (цепные, базисные), абсолютное значение 1% прироста. Результаты оформите в виде таблицы. Сделайте выводы.
| Год | 1994 | 1995 | 1996 | 1997 | 1998 |
| Перевезено грузов, млн. тонн | 300 | 350 | 380 | 400 | 420 |
Решение:
Произведем анализ динамики перевозки грузов, вычислив для этого абсолютные и относительные показатели динамики. Результаты представим в таблице.
| Годы | 1994 | 1995 | 1996 | 1997 | 1998 |
| Перевезено грузов, млн. т | 300 | 350 | 380 | 400 | 420 |
| Абсолютный прирост, млн. т | |||||
| - цепной | - | 50 | 30 | 20 | 20 |
| - базисный | 0 | 50 | 80 | 100 | 120 |
| Темп роста, % | |||||
| - цепной | - | 116,7 | 108,6 | 105,3 | 105,0 |
| - базисный | 100 | 116,7 | 126,7 | 133,3 | 140,0 |
| Темп прироста, % | |||||
| - цепной | - | 16,7 | 8,6 | 5,3 | 5,0 |
| - базисный | 0 | 16,7 | 26,7 | 33,3 | 40,0 |
| Абсолютное содержание 1% прироста, млн. т | - | 3 | 3,5 | 3,8 | 4 |
Среднегодовой объем перевозок:
![]() (млн. т)
(млн. т)
Среднегодовой абсолютный прирост:
![]() (млн. т)
(млн. т)
Среднегодовой темп роста:
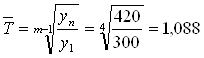 или 108,8%
или 108,8%
Среднегодовой темп прироста:
![]()
Таким образом, видим, что в 1994 – 1998г.г. тенденция объема перевозок характеризуется постоянным ростом. В целом за рассматриваемый период объем перевозок увеличился на 120 млн. т или 40%. В среднем объем перевозок в год увеличивался на 30 млн. т или на 8,8%.
Задача 12.
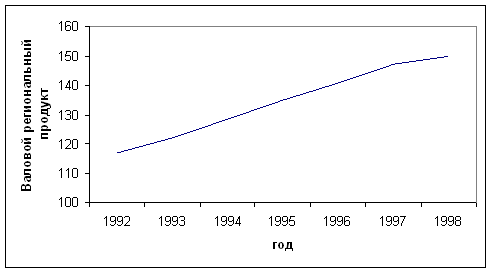
Валовой региональный продукт Нижегородской области за 1992 – 1998 г.г. в сопоставимых ценах характеризуется следующими данными:
| Год | 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 |
| Валовой региональный продукт | 117,0 | 122,2 | 128,6 | 134,8 | 140,7 | 147,0 | 150,0 |
Для анализа динамики определите:
1) абсолютные приросты;
2) темпы роста и прироста;
3) среднегодовой уровень;
4) Среднегодовой абсолютный прирост;
5) Среднегодовой темп роста и прироста;
6) Постройте график динамики валового регионального продукта.
Решение:
Произведем анализ динамики перевозки грузов, вычислив для этого абсолютные и относительные показатели динамики. Результаты представим в таблице.
| Годы | 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 |
| Перевезено грузов, млн. т | 117,0 | 122,2 | 128,6 | 134,8 | 140,7 | 147,0 | 150,0 |
| Абсолютный прирост, млн. т | |||||||
| - цепной | - | 5,2 | 6,4 | 6,2 | 5,9 | 6,3 | 3 |
| - базисный | 0 | 5,2 | 11,6 | 17,8 | 23,7 | 30 | 33 |
| Темп роста, % | |||||||
| - цепной | - | 104,4 | 105,2 | 104,8 | 104,4 | 104,5 | 102,0 |
| - базисный | 100 | 104,4 | 109,9 | 115,2 | 120,3 | 125,6 | 128,2 |
| Темп прироста, % | |||||||
| - цепной | - | 4,4 | 5,2 | 4,8 | 4,4 | 4,5 | 2,0 |
| - базисный | 0 | 4,4 | 9,9 | 15,2 | 20,3 | 25,6 | 28,2 |
| Абсолютное содержание 1% прироста, млн. т | - | 1,17 | 1,222 | 1,286 | 1,348 | 1,407 | 1,47 |
Среднегодовой валовой региональный продукт:
![]()
Среднегодовой абсолютный прирост:
![]()
Среднегодовой темп роста:
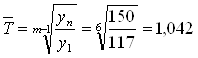 или 104,2%
или 104,2%
Среднегодовой темп прироста:
![]()
Таким образом, видим, что в 1992 – 1998г.г. тенденция валового регионального продукта характеризуется постоянным ростом. В целом за рассматриваемый период валовой региональный продукт увеличился на 33 или 28,2%. В среднем валовой региональный продукт в год увеличивался на 5,5 или на 4,2%.
Изобразим ряд динамики графически:
Задача 13.
Имеются следующие данные по трем товарным группам:
| Товарная группа | Товарооборот в мае p0q0 | Товарооборот в июне p1q1 | Изменение цен в июне по сравнению с маем, % |
| А | 93 | 97 | +3 |
| В | 25 | 30 | +5 |
| С | 40 | 50 | Без изменения |
Определить:
1) общий индекс товарооборота;
2) индивидуальные и общий индексы цен;
3) индивидуальные и общий индексы объема физических продаж;
4) изменение товарооборота за счет изменения цен и объема реализованной продукции.
Решение:
1. Определим индивидуальные индексы: цен, физического объема товарооборота и товарооборота в фактических ценах;
| Товарные группы | Индекс цен | Индекс товарооборота в фактических ценах | Индекс физического объема |
| А | 1,03 | 97 / 93 = 1,043 | 1,043 / 1,03 = 1,013 |
| В | 1,05 | 25 / 30 = 0,833 | 0,833 / 1,05 = 0,793 |
| С | 1,0 | 40 / 50 = 0,8 | 0,8 / 1,0 = 0,8 |
2. Общий индекс физического объема товарооборота (общий):
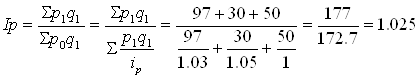 или 102,5%
или 102,5%
3. Общий индекс товарооборота в фактических ценах:
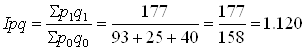 или 112%
или 112%
4. Общий индекс физического объема продаж:
Iq = Ipq / Ip = 1,120 / 1,025 = 1,093 или 109,3%
5. Прирост товарооборота:
- всего Δpq = Σ p1q1 – Σ p0q0 = 177 - 158 = 19
- за счет изменения цен Δpq (р)= 177 – 172,7 = 4,3
- за счет изменения физического объема Δpq (q) = 19 – 4,3 = 14,7
Таким образом, товарооборот по товарным группам вырос на 19 ден. ед или на 12% в июне по сравнению с маем, причем на 14,7 ден. ед. или на 9,3% он вырос за счет увеличения физического объема продаж, а на 4,3 ден. ед. или на 2,5% за счет роста цен.
Список использованной литературы:
1. Гусаров В.М., «Теория статистики», – М.: Аудит, ЮНИТИ, 2002;
2. Ефимова М.П., Петрова Е.В., Румянцев В.Н., «Общая теория статистики», - М.: “Инфра - М”, 2003;
3. «Практикум по статистике: Учеб. пособие для вузов» / Под ред. В.М. Симчеры / ВЗФЭИ. – М.: ЗАО «Финстатинформ», 2000.
Похожие работы
... , табличные характеристики связи. Это в свою очередь потребовало решения соответственно теоретико-методологических проблем. Глава 2. Абсолютные и относительные величины 2.1. Понятие, формы выражения и виды статистических показателей Статистическое исследование независимо от его масштабов и целей всегда завершается расчетом и анализом различных по виду и форме выражения статистических ...
... наблюдения – можно ли распространить результаты выборочной совокупности на генеральную совокупность или нет, следовательно, проверка выборочной совокупности на точность это необходимая часть анализа при несплошном наблюдении. Существуют два вида оценок статистических показателей на точность: точечная и интервальная. Точечная представляет собой оценку параметра в генеральной совокупности одним чи
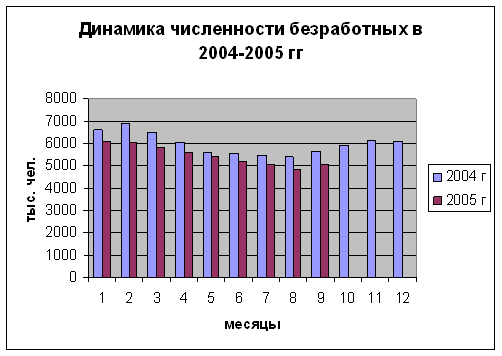
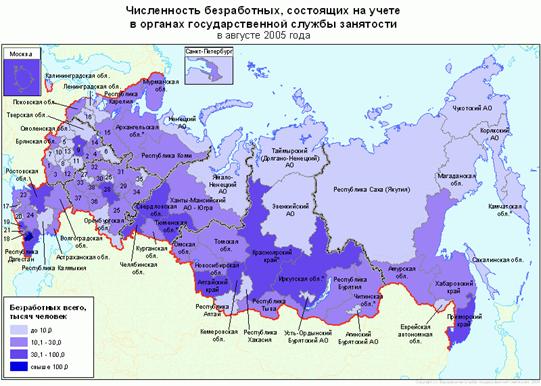
... Федерации, можно отметить, что она носит сезонный характер: в зимний период времени безработных больше, чем в летний, что связано с сезонным характером большинства работ. Анализ статистических показателей безработицы в 2003 -2004 гг. в Российской Федерации позволил сделать следующие выводы: · среднегодовая численность населения сократилась на 0,8 млн. чел.; · сокращение численности людей, ...
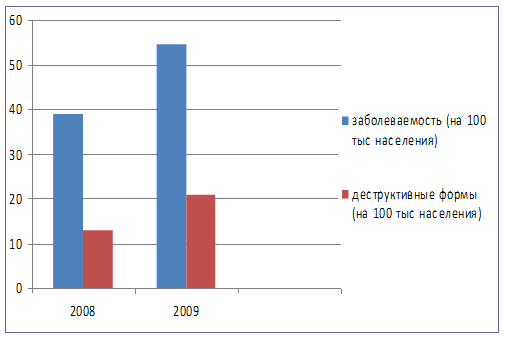
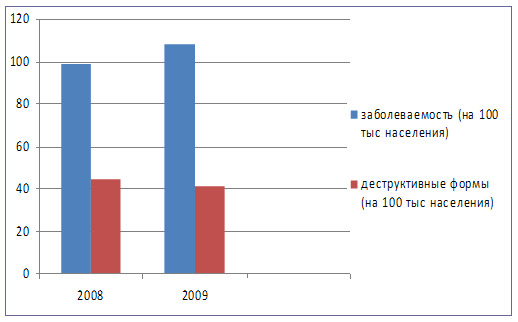
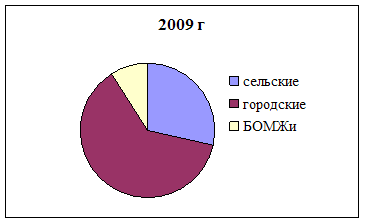
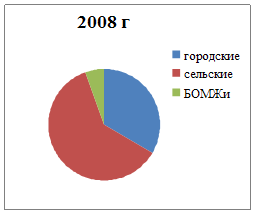
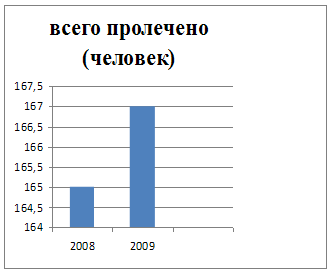
... 100 25 400 30 900 25 300 Всего: город село 38 700 31 500 38 600 31 500 7. Выводы и предложения При анализе статистических показателей работы Государственного учреждения здравоохранения «Областной противотуберкулезный диспансер № 8» за 2008–2009 годы можно сделать заключение, что: - разница населения между Южноуральским городским округом и Увельским муниципальным ...
0 комментариев