Контрольная работа по учебной дисциплине
«Экономико-математические методы и модели»
Введение
Объектом исследования является Республиканское унитарное предприятие «Укрупненная типография им. А. Т. Непогодина»
Типография является единственным специализированным предприятием в Республике Беларусь, которая обеспечивает потребности страны по билетной продукции, начиная от простейших билетов в клубы и кончая киноконцертным залом «Минск». В Бобруйске и во всем нашем регионе, в отличие от многих других, предприятия, фирмы не испытывают трудностей с товарно-транспортными накладными нового образца. Ими типография обеспечивает и значительную часть Гомельской области.
Но, хотя газеты по своей значимости - продукция №1, однако по доходности, объемам они не определяющие. Основная продукция - бланки, товарно-транспортные накладные, билеты, конверты и т.п.
Наряду с ростом объемов выросло и качество, сейчас типография печатает полноцветную продукцию.
Учитывая высокую степень износа основных средств завода, главным источником повышения конкурентоспособности его продукции является реконструкция и обновление производства. Чтобы этого достичь, надо продолжить выполнение плана технического перевооружения в соответствии с которым должны приобрести 4единицы новой техники. Это ризограф для оперативной печати большого формата, ниткосшивательная машина для скрепления блоков,что позволит выпускать высококачественные ежедневник, еженедельники, журналы, книги и т.д., термобиндер - аппарат, позволяющий склеивать блоки, приклеивать обложки, без такого оборудования не будет высокого качества на конечном этапе, купить резальные машины, поскольку теперяшние эксплуатируются более 25 лет и венок всему - «Доминанта 725С» - печатная машина последнего образца.
Принимая во внимание, что тарифы на электроэнергию имеют тенденцию роста, для предприятия актуально анализировать эффективность использования как электроэнергии, так и других ресурсов, чтобы выдерживать конкуренцию на рынках как Беларуси. Важнейшим эффективным инструментом поиска резервов снижения себестоимости продукции является внедрение экономико-математического моделирования в практику хозяйствования.
Производственная информация об объемах выпускаемой продукции и потребляемой в течение календарного года электроэнергии представлена в табл.1.
Таблица 1. Исходные данные
| Месяцы | Валовый выпуск, млн. руб.
| Электроэнергия, кВт-час.
|
| Январь | 14,68759467 | 7,52132472 |
| Февраль | 13,24504199 | 9,34813787 |
| Март | 20,16645413 | 12,3224191 |
| Апрель | 21,69279603 | 14,4152562 |
| Май | 20,77057056 | 16,58371 |
| Июнь | 21,44564545 | 17,476016 |
| Июль | 23,660205 | 16,7798364 |
| Август | 24,58927872 | 15,313543 |
| Сентябрь | 22,653 | 13,2240118 |
| Октябрь | 20,34123684 | 10,1868578 |
| Ноябрь | 21,98596881 | 8,20990502 |
| Декабрь | 22,61916361 | 7,4279725 |
На основе исходных данных (табл.1) рассчитывается однофакторная линейная модель.
![]() (1)
(1)
Паспорт модели характеризуется следующими данными (табл.2):
Таблица 2. Паспорт модели
| 0,5522939 | 0,99325702 |
| 0,3043097 | 6,36274449 |
| 0,2477747 | 3,42536228 |
| 3,293889 | 10 |
| 38,647552 | 117,331068 |
Паспортные данные показывают Fcт=3,293889>1,9
Следовательно, модель в целом значима.
Коэффициент детерминации ![]() и характеризует умеренный уровень связи между потребляемой электроэнергией и объемом выпускаемой продукции.
и характеризует умеренный уровень связи между потребляемой электроэнергией и объемом выпускаемой продукции.
Оценки коэффициентов регрессии ![]() и
и ![]() значимы, так как соответствующие расчетные значения критериев Стьюдента превышают табличные значения.
значимы, так как соответствующие расчетные значения критериев Стьюдента превышают табличные значения.
![]()
![]()
Таким образом, модель в целом и ее коэффициенты значимы. С ростом объема выпуска продукции увеличиваются потребление электроэнергии, причем при увеличении (уменьшении) выпуска продукции в среднем на 1 млн. руб. потребление электроэнергии увеличивается на 552,3 кВт. ч.
Результаты моделирования представлены в таблице 2.
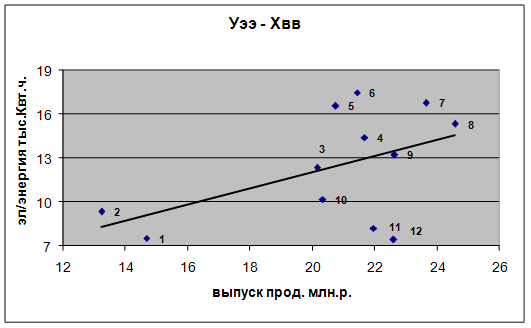
ü График модели (1) представлен на рисунке 1. Линия графика разделяет режимы работы предприятия на две группы (кластера). Точки на рисунке, расположенные ниже линии, соответствуют режимам работы предприятия в январе, июне, сентябре, октябре, ноябре и декабре и характеризуются более экономичным использованием электроэнергии по сравнению с остальными режимами.
| месяцы | Х - вып.т.прод. | газеты | ватман | У - р-д эн. |
| январь | 14,68759467 | 9,987768 | 4,69983 | 7,5213247 |
| февраль | 13,24504199 | 5,5629176 | 7,68212 | 9,3481379 |
| март | 20,16645413 | 9,07489 | 11,0915 | 12,322419 |
| апрель | 21,69279603 | 8,243279 | 13,4495 | 14,415256 |
| май | 20,77057056 | 5,192643 | 15,5779 | 16,58371 |
| июнь | 21,44564545 | 4,718042 | 16,7276 | 17,476016 |
| июль | 23,660205 | 7,09806 | 16,6214 | 16,779836 |
| август | 24,58927872 | 9,909247 | 15,983 | 15,313543 |
| сентябрь | 22,653 | 14,04486 | 8,60814 | 13,224012 |
| октябрь | 20,34123684 | 12,611567 | 7,72967 | 10,186858 |
| ноябрь | 21,98596881 | 14,539399 | 6,23117 | 8,209905 |
| декабрь | 22,61916361 | 16,964373 | 5,65479 | 7,4279725 |
| 14,68759467 | 148,80899 | |||
Низкая экономичность использования электроэнергии в феврале, марте, апреле, мае, июне, июле и августе объясняется, прежде всего, высоким уровнем выпуска ватманов, как наиболее электроемкой продукции, по сравнению с выпуском газет, как наиболее массовой и менее энергоемкой продукцией.
| январь | 0,512 | 0,6199 | 0,1079 | |
| февраль | 0,7057 | 0,6272 | -0,0785 | неэконом |
| март | 0,611 | 0,6015 | -0,0095 | неэконом |
| апрель | 0,6645 | 0,5981 | -0,0664 | неэконом |
| май | 0,7984 | 0,6001 | -0,1983 | неэконом |
| июнь | 0,8148 | 0,5986 | -0,2162 | неэконом |
| июль | 0,7092 | 0,5943 | -0,1149 | неэконом |
| август | 0,6227 | 0,5927 | -0,03 | неэконом |
| сентябрь | 0,5837 | 0,596 | 0,0123 | |
| октябрь | 0,5007 | 0,6011 | 0,1004 | |
| ноябрь | 0,3734 | 0,5975 | 0,2241 | |
| декабрь | 0,3283 | 0,5962 | 0,2679 |
Кроме указанных внутренних производственных факторов на энергоемкость продукции влияют и погодно-климатические условия, Повышенный расход электроэнергии в феврале обусловлен резким снижением температуры воздуха, когда температура снижается, а помещения плохо отапливаются, и для обогрева используются электрообогреватели, что и приводит к неэкономичному режиму.
Использование графической информации (рис.1) позволяет дать качественную характеристику режимов работы предприятия.
Оценка режимов функционирования предприятия по эффективности использования электроэнергии проводится путем сравнения фактических и расчетных значений ресурсоемкости (![]() и
и ![]() ). Для этой цели рассчитываются значения
). Для этой цели рассчитываются значения ![]() (табл.3).
(табл.3).
Таблица 3.
|
|
кВт-ч |
|
|
|
|
|
|
|
| 14,687594 | 7,521324 | 8,1118689 | 0,993257 | 9,105125 | -1,583801 | 2,508426 | 0,5120 | 0,6199 |
| 13,245041 | 9,348137 | 7,3151559 | 0,993257 | 8,308412 | 1,039725 | 1,081028 | 0,7057 | 0,6272 |
| 20,166454 | 12,32241 | 11,13781 | 0,993257 | 12,13106 | 0,191353 | 0,036615 | 0,6110 | 0,6015 |
| 21,692796 | 14,41525 | 11,980799 | 0,993257 | 12,97405 | 1,4412 | 2,077058 | 0,6645 | 0,5981 |
| 20,770570 | 16,58371 | 11,471459 | 0,993257 | 12,46471 | 4,118994 | 16,96610 | 0,7984 | 0,6001 |
| 21,445645 | 17,47601 | 11,844299 | 0,993257 | 12,83755 | 4,63846 | 21,51530 | 0,8148 | 0,5986 |
| 23,660205 | 16,77983 | 13,067387 | 0,993257 | 14,06064 | 2,719192 | 7,394007 | 0,7092 | 0,5943 |
| 24,589278 | 15,31354 | 13,580509 | 0,993257 | 14,57376 | 0,739777 | 0,547270 | 0,6227 | 0,5927 |
| 22,653 | 13,22401 | 12,511138 | 0,993257 | 13,50439 | -0,280383 | 0,078614 | 0,5837 | 0,596 |
| 20,341236 | 10,18685 | 11,234341 | 0,993257 | 12,22759 | -2,04074 | 4,164620 | 0,5007 | 0,6011 |
| 21,985968 | 8,209905 | 12,142716 | 0,993257 | 13,13597 | -4,926068 | 24,26615 | 0,3734 | 0,5975 |
| 22,619163 | 7,427972 | 12,492426 | 0,993257 | 13,48568 | -6,057711 | 36,69585 | 0,3283 | 0,5962 |
| 14,687594 | 148,8089 | 148,8089 | 117,331068 |
Равенство значений ![]() в паспорте модели с полученным в таблице обеспечивает достоверность полученных значений
в паспорте модели с полученным в таблице обеспечивает достоверность полученных значений ![]() .
.
Условие ![]() <
<![]() позволяет уточнить экономичные по расходу электроэнергии режимы. Для неэкономичных режимов фактическая ресурсоемкость будет превосходить расчетную. Анализ характеристик электроемкости позволяет выделить мартовский режим с наименьшей электроемкостью.
позволяет уточнить экономичные по расходу электроэнергии режимы. Для неэкономичных режимов фактическая ресурсоемкость будет превосходить расчетную. Анализ характеристик электроемкости позволяет выделить мартовский режим с наименьшей электроемкостью.
Таблица 4. Ортогональные полиномы Чебышева
|
|
|
|
|
|
|
|
|
|
|
|
| -5,5 | 18,333 | -49,5 | 113,1429 | -220 | 360 | -484,615 | 516,92308 | -410,49774 | 216,05144 | 2264,8081 |
| -4,5 | 8,333 | 4,5 | -92,5714 | 380 | -1014,55 | 1982,52 | -2866,5734 | 2948,1201 | -1944,463 | 2390,2321 |
| -3,5 | 0,333 | 31,5 | -113,1429 | 140 | 360 | -2211,61 | 5592,1678 | -8471,1806 | 7561,8004 | 4311,2356 |
| -2,5 | -5,667 | 37,5 | -44,5714 | -193,333 | 818,1818 | -731,329 | -3054,5455 | 11307,347 | -16203,86 | 3623,5584 |
| -1,5 | -9,667 | 28,5 | 41,14286 | -293,333 | 130,9091 | 1797,48 | -3477,4825 | -3806,4336 | 19444,63 | 3908,0002 |
| -0,5 | -11,667 | 10,5 | 96 | -133,333 | -654,545 | 1233,57 | 3289,5105 | -7836,775 | -9074,161 | 3317,9904 |
| 0,5 | -11,667 | -10,5 | 96 | 133,333 | -654,545 | -1233,57 | 3289,5105 | 7836,775 | -9074,161 | 5292,417 |
| 1,5 | -9,667 | -28,5 | 41,14286 | 293,333 | 130,9091 | -1797,48 | -3477,4825 | 3806,4336 | 19444,63 | 7635,6139 |
| 2,5 | -5,667 | -37,5 | -44,5714 | 193,333 | 818,1818 | 731,329 | -3054,5455 | -11307,347 | -16203,86 | 6957,5617 |
| 3,5 | 0,333 | -31,5 | -113,143 | -140 | 360 | 2211,61 | 5592,1678 | 8471,1806 | 7561,8004 | 8052,5497 |
| 4,5 | 8,333 | -4,5 | -92,5714 | -380 | -1014,55 | -1982,52 | -2866,5734 | -2948,1201 | -1944,463 | 4983,0893 |
| 5,5 | 18,333 | 49,5 | 113,1429 | 220 | 360 | 484,615 | 516,92308 | 410,49774 | 216,05144 | 9460,0912 |
|
|
|
|
|
|
|
|
|
|
|
|
| 1568014937 | 568761782 | 144001611 | 28687821 | 4806982 | 707200 | 94134,9 | 11583 | 1334,667 | 143 | 12 |
| 5,2552E-07 | -2,0385E-05 | 4,2318E-06 | -8,4E-06 | 8,161E-06 | 2,1572E-05 | 0,009435972 | 0,0134639 | -0,327216 | -0,1282615 | 12,402316 |
| 1,8021E-07 | 2,99216E-07 | 5,9466E-07 | 1,332E-06 | 3,255E-06 | 8,4855E-06 | 2,32582E-05 | 6,63E-05 | 0,0001953 | 0,0005967 | 0,00206 |
| 0,99999967 | 0,007135924 | #Н/Д | #Н/Д | #Н/Д | #Н/Д | #Н/Д | #Н/Д | #Н/Д | #Н/Д | #Н/Д |
| 306312,319 | 1 | #Н/Д | #Н/Д | #Н/Д | #Н/Д | #Н/Д | #Н/Д | #Н/Д | #Н/Д | #Н/Д |
| 155,978568 | 5,09214E-05 | #Н/Д | #Н/Д | #Н/Д | #Н/Д | #Н/Д | #Н/Д | #Н/Д | #Н/Д | #Н/Д |
|
|
|
|
|
|
|
|
|
|
|
|
| 4,3087E-05 | 0,244242786 | 0,00025074 | 0,0020246 | 0,0003202 | 0,00032911 | 8,381538722 | 2,0997336 | 142,90316 | 2,3524964 | 1845,8094 |
| S3 | S2 | S1 | S0 | |||||||
| 4,22747722 | 4,227520304 | 12,609059 | 155,51222 | |||||||
| D3 | D2 | D1 | D0 | |||||||
| 0,52843465 | 0,469724478 | 1,2609059 | 14,137475 | |||||||
| R² | R² | R² | ||||||||
| 0,97281579 | 0,97281551 | 0,9189192 |
| A4 | A2 | A0 | Y* | (Y-Y*) |
|
| 1,067614165 | -5,998843 | 12,402316 | 7,4710872 | 0,050237 | 0,0025238 |
| -0,87349735 | -2,726687 | 12,402316 | 8,8021315 | 0,546006 | 0,29812299 |
| -1,06761416 | 0 | 12,402316 | 11,334702 | 0,987717 | 0,97558498 |
| -0,4205707 | 1,8543307 | 12,402316 | 13,836076 | 0,57918 | 0,3354495 |
| 0,38822419 | 3,163193 | 12,402316 | 15,953733 | 0,629977 | 0,3968706 |
| 0,905853299 | 3,8176241 | 12,402316 | 17,125794 | 0,350222 | 0,1226557 |
| 0,905853299 | 3,8176241 | 12,402316 | 17,125794 | -0,345957 | 0,11968644 |
| 0,38822419 | 3,163193 | 12,402316 | 15,953733 | -0,64019 | 0,40984367 |
| -0,4205707 | 1,8543307 | 12,402316 | 13,836076 | -0,612064 | 0,37462277 |
| -1,06761416 | -0,108963 | 12,402316 | 11,225739 | -1,038881 | 1,07927469 |
| -0,87349735 | -2,726687 | 12,402316 | 8,8021315 | -0,592226 | 0,35073217 |
| 1,067614165 | -5,998843 | 12,402316 | 7,4710872 | -0,043115 | 0,00185888 |
| 148,93809 | 0,128997 | 4,46722619 |
Таблица 6. Динамика расчета полиномиальной модели 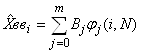
| 1,7676E-20 | 7,08285E-20 | -2,78E-19 | -0,000767 | 0,0010333 | -3,871E-18 | 0,006334429 | 0,0155122 | -0,168548 | 0,6489895 | 20,654693 |
| 2,243E-19 | 3,72422E-19 | 7,4014E-19 | 1,658E-18 | 4,051E-18 | 1,0562E-17 | 2,89484E-17 | 8,253E-17 | 2,431E-16 | 7,427E-16 | 2,564E-15 |
| 1 | 8,88178E-15 | #Н/Д | #Н/Д | #Н/Д | #Н/Д | #Н/Д | #Н/Д | #Н/Д | #Н/Д | #Н/Д |
| 1,6061E+29 | 1 | #Н/Д | #Н/Д | #Н/Д | #Н/Д | #Н/Д | #Н/Д | #Н/Д | #Н/Д | #Н/Д |
| 126,701428 | 7,88861E-29 | #Н/Д | #Н/Д | #Н/Д | #Н/Д | #Н/Д | #Н/Д | #Н/Д | #Н/Д | #Н/Д |
|
|
|
|
|
|
|
|
|
|
|
|
| 4,8746E-32 | 2,94861E-30 | 1,0818E-30 | 16,859527 | 5,1321165 | 1,0596E-29 | 3,777160888 | 2,7871872 | 37,915753 | 60,229796 | 5119,3959 |
| S5 | S3 | S4 | S2 | S1 | S0 | |||||
| 6,69269464 | 11,724811 | 6,5926946 | 28,584338 | 66,500091 | 126,72989 | |||||
| D5 | D3 | D4 | D2 | D1 | D0 | |||||
| 1,09878244 | 1,4656014 | 0,9418135 | 3,1760376 | 6,6500091 | 11,520899 | |||||
| R² | R² | R² | R² | |||||||
| 0,949 97838 | 0,9074819 | 0,9479784 | 0,7744467 | 0,4752612 |
Таблица 7.
| Y -Y^ | ( Y- Y^) 2 | Уээi/Хввi | У^ээi/Xввi.сгл. | |||
| -0,238917 | 8,99571804 | 8,756800841 | 1,2354768 | 25,62213 | 0,5120869 | 0,5962039 |
| -0,238917 | 8,11219688 | 7,873279684 | -1,4748573 | 4850,029 | 0,7057839 | 0,5944323 |
| -0,238917 | 12,3513582 | 12,11244096 | -0,209969 | 5,156329 | 0,611035 | 0,6006232 |
| -0,238917 | 13,2861976 | 13,04728041 | -1,3679696 | 1160,394 | 0,6645178 | 0,6014568 |
| -0,238917 | 12,7213614 | 12,48244419 | -4,1012658 | 821,4543 | 0,7984234 | 0,6009678 |
| -0,238917 | 13,1348249 | 12,89590772 | -4,5801023 | 18184,41 | 0,8148978 | 0,6013299 |
| -0,238917 | 14,4911776 | 14,25226039 | -2,5275696 | 6961,603 | 0,7092005 | 0,6023727 |
| -0,238917 | 15,0602074 | 14,82129019 | -0,4922498 | 44,23303 | 0,6227731 | 0,6027542 |
| -0,238917 | 13,8742942 | 13,63537704 | 0,411367 | 3,571383 | 0,5837642 | 0,6019237 |
| -0,238917 | 12,458407 | 12,21948978 | 2,0326398 | 110,3811 | 0,500798 | 0,600725 |
| -0,238917 | 13,4657568 | 13,22683961 | 5,0169346 | 12070,95 | 0,3734157 | 0,6016037 |
| -0,238917 | 13,8535701 | 13,61465287 | 6,1866809 | 12404,77 | 0,3283929 | 0,6019079 |
| 148,9380637 | 0,1291157 | 105,89782 |
| A7 | A6 | A2 | A1 | A0 | X* |
|
|
| 0,3715102 | 0,3719756 | -3,089985 | -3,5694423 | 20,654693 | 14,738751 | -0,051156 | 0,00261694 |
| -1,519815 | -1,048295 | -1,404508 | -2,9204528 | 20,654693 | 13,761622 | -0,51658 | 0,26685459 |
| 1,6954386 | 0,3719756 | -0,056126 | -2,2714633 | 20,654693 | 20,394517 | -0,228063 | 0,05201274 |
| 0,5606434 | 0,8453994 | 0,95516 | -1,6224738 | 20,654693 | 21,393422 | 0,299374 | 0,08962509 |
| -1,377967 | 0,1352638 | 1,6293509 | -0,9734843 | 20,654693 | 20,067856 | 0,702714 | 0,49380733 |
| -0,945663 | -0,676319 | 1,9664463 | -0,3244948 | 20,654693 | 20,674662 | 0,770983 | 0,59441479 |
| 0,9456628 | -0,676319 | 1,9664463 | 0,3244948 | 20,654693 | 23,214978 | 0,445227 | 0,19822748 |
| 1,3779666 | 0,1352638 | 1,6293509 | 0,9734843 | 20,654693 | 24,770758 | -0,181479 | 0,03293477 |
| -0,560643 | 0,8453994 | 0,95516 | 1,6224738 | 20,654693 | 23,517082 | -0,864038 | 0,74656202 |
| -1,695439 | 0,3719756 | -0,056126 | 2,2714633 | 20,654693 | 21,546567 | -1,20533 | 1,45281965 |
| 1,5198154 | -1,048295 | -1,404508 | 2,9204528 | 20,654693 | 22,642158 | -0,656189 | 0,4305843 |
| -0,37151 | 0,3719756 | -3,089985 | 3,5694423 | 20,654693 | 21,134615 | 1,484549 | 2,20388494 |
| 247,85699 | 0,235699 | 6,56434464 |
ü Полиномиальные модели с использованием ортогональных на дискретном множестве полиномов Чебышева (табл.4) рассчитываются с использованием двухпорогового метода, при котором значимые компоненты полиномиальной регрессии выделяются при соблюдении следующих двух условий:
1) ![]()
2) ![]()
Где ![]() и
и ![]() - оценки дисперсии на (
- оценки дисперсии на (![]() )-ом и
)-ом и ![]() -ом шагах.
-ом шагах.
![]() - значение оценки коэффициента детерминации.
- значение оценки коэффициента детерминации.
Для построения полиномиальных моделей рассчитываются 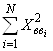 и
и ![]() , и средние значения:
, и средние значения:
![]()
![]()
Динамика расчета полиномиальной модели
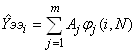
представлена в таблице 5.
Паспорт полиномиальных моделей определяется на основе исходных данных об ![]() и
и ![]() и рассчитанных полиномах
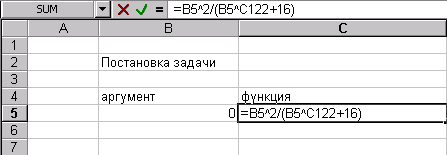
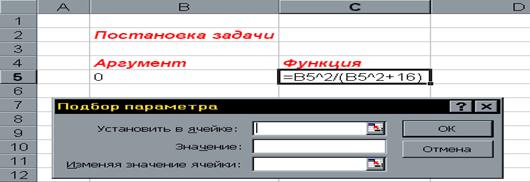
и рассчитанных полиномах ![]() , введенных в компьютер. При использовании Excel массив задается блоком в пять строк и одиннадцать столбцов, а все остальные манипуляции аналогичны, как и для линейной однофакторной модели (1).
, введенных в компьютер. При использовании Excel массив задается блоком в пять строк и одиннадцать столбцов, а все остальные манипуляции аналогичны, как и для линейной однофакторной модели (1).
На десятом шаге при определении ![]() значение оценки дисперсии возрастает по сравнению с предыдущим шагом.
значение оценки дисперсии возрастает по сравнению с предыдущим шагом.
Таким образом, полиномиальная модель имеет вид:
![]()
Расчет значений ![]() показал совпадение значений
показал совпадение значений 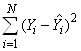 с паспортом модели.
с паспортом модели.
Расчет полиномиальной модели:
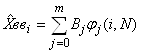
приведен в таблице 6.
В данном случае значение оценки коэффициента детерминации превысило пороговое значение на пятом шаге.
Таким образом, полиномиальная модель имеет вид:
![]()
Расчет значений ![]() показал совпадение
показал совпадение ![]() с паспортными данными.
с паспортными данными.
![]()
0,2970017 | 6,2060563 |
| 0,2983727 | 3,2553482 |
| 4,2525808 | 10 |
| 45,06584 | 105,97292 |
Сравнение данной модели, рассчитанной по сглаженным значениям объема выпускаемой продукции, свидетельствует об уточнении самой модели и ее параметров. (Табл. 7, Рис 2).
Рассчитанные характеристики ресурсоемкости, отличаясь по своим значениям, полностью подтверждают качественную картину – те же режимы работы предприятия. Таким образом, для прикладного анализа эффективности использования электроэнергии допустимо использовать исходные данные без сглаживания.
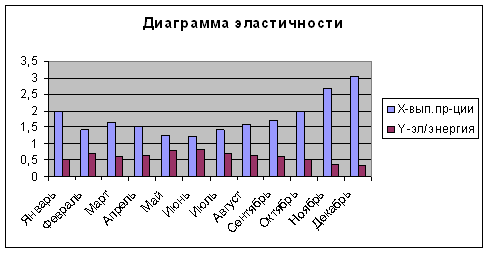
Рис. 2. Диаграмма эластичности
ü Оценим эластичность потребления электроэнергии по объему выпускаемой продукции по модели без учета и с учетом сглаживания.
1) ![]()
2) ![]()
Таким образом, при изменении объема выпускаемой продукции на 1%, потребление электроэнергии изменится на 0,331588 (0,367764)%, что свидетельствует об умеренной связи этих производственных факторов.
Для расчета оценок эластичности по месяцам года умножим значения соответствующих ресурсоемкостей на значения предельной электроемкости для каждой однофакторной модели. Как следует из диаграммы, эластичность наибольшая в феврале и наименьшая в апреле, что соответствует наименьшему и наибольшему выпуску продукции. Следовательно, управлять расходом электроэнергии целесообразно при меньших объемах выпускаемой продукции.
ü Рассчитанные полиномиальные модели производственных факторов, отражающие тенденцию их изменения, могут быть использованы как для первичной обработки производственной информации, так и для прогноза на очередной временной интервал, например, на очередной месяц.
Непосредственное использование для прогноза полученных полиномиальных моделей, как свидетельствует практика, зачастую приводит к большим неточностям. Необходимо переходить к так называемым «усеченным» моделям, у которых наибольшая степень полинома снижается до линейной или квадратичной.
Так, полиномиальная модель, характеризующая изменение расхода энергоресурса, будет иметь вид:
![]()
а для объема выпускаемой продукции получим:
![]()
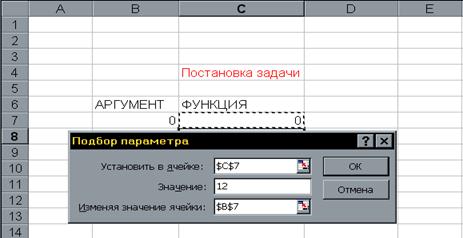
Прогнозные значения на следующий шаг будут равны:
![]()
![]()
Полученные прогнозные значения соответствуют экономичному режиму потребления электроэнергии.
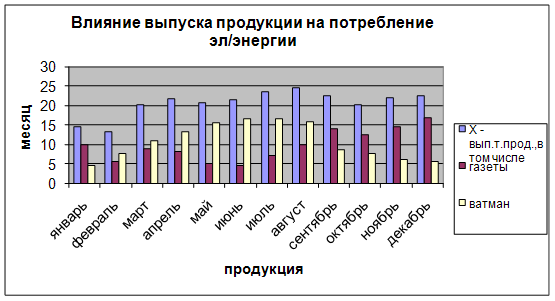
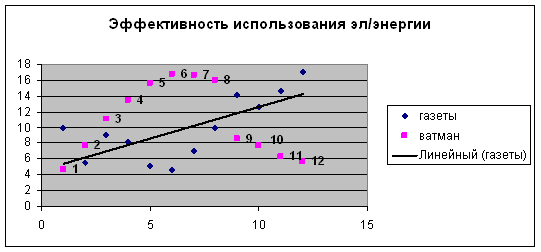
По диаграмме мы видим разделение на 3 режима:
К первому режиму относится январь месяц - это экономичный режим.
Ко второй режиму относятся февраль, март, апрель, май, июнь и июль месяцы - это неэкономичный режим.
В феврале месяце большое потребление электроэнергии обусловлено резким снижением температуры воздуха, что повлекло за собой обогрев помещений при помощи электрооборудования.
С марта по июль были большие заказы на ватман, который по сравнение с газетой является более электроемкой продукцией.
К третьему режиму относятся сентябрь, октябрь, ноябрь, декабрь месяцы и является экономичным режимом.
Выводы:
1. Проведенный анализ показывает, что предприятие имеет резервы снижения электроемкости за счет усовершенствования и обновления основных производственных фондов.
2. Умеренный уровень связи между производственными факторами может отражает линейную модель связи факторов.
Литература:
1. Бородич С.А., Эконометрика: Учебное пособие. Мн. Новое знание, 2001
2. Желудкевич М.Е., Моделирование ресурсосбережения: Учебно-методическое пособие. Мн., БГЭУ, 2002
3. Экономико-математические методы и модели. Учебное пособие. Под редакцией А.В.Кузнецова. Мн.: БГЭУ, 1999
4. Анисимова Ж.Н. Основы экономической информатики. Лабораторный практикум. Мн., БГЭУ, 1999
Похожие работы
... системы цен по остальным товарам. Конец XIX – начало XX века ознаменовались широким использованием математики в экономике. В XX в. математические методы моделирования используются столь широко, что почти все работы, удостоенные Нобелевской премии по экономике, связаны с их применением (Д. Хикс, Р. Солоу, В. Леонтьев, П. Самуэльсон, Л. Канторович и др.). Развитие предметных дисциплин в большинстве ...
... моделей экстремальных планов и экстремальных значений целевой функции быть не может. Таким образом, для принятия оптимального решения любой экономической задачи необходимо построить ее экономико-математическую модель, по структуре включающую в себе систему ограничений, целевую функцию, критерий оптимальности и решение. Методика построения экономико-математической модели состоит в том, чтобы ...
... . Специалист для которого MS Excel является именно тем средством которое позволяет облегчить и ускорить его работу, должен знать и уметь использовать в повседневной работе новейшие экономико-математические методы и модели, предлагаемые новыми прикладными программами. Традиционный способ изучения экономико-математических методов заключается не только в определении их назначения и сути, ...
... производственной функции, моделей поведения фирмы, моделей общего экономического равновесия, прежде всего модели Л. Вальраса и ее модификаций. Глава 2. История развития экономико-математического моделирования в США Для характеристики математического направления в экономике за последние 80 – 90 лет приведу лишь некоторые результаты, сыгравшие заметную роль в его развитии. Как в теоретическом, ...


0 комментариев