![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Отчет по лабораторной работе «Определение напряжений в элементах конструкций электротензометрированием»
Отчет по лабораторной работе «Определение напряжений в элементах конструкций электротензометрированием»
Цель работы: изучение методики и экспериментальное определение напряжений в элементах конструкций электротензометрированием; сравнение расчетных и экспериментальных значений напряжений.
Экспериментальное определение напряжений проводится при создании, сдаче в эксплуатацию или после определенного срока работы ответственных конструкций с целью оценки их прочности. Устройства, преобразующие механические величины в электрические, называются датчиками (деформации -(тензорезистор), линейных или угловых перемещений, давлений, усилий, скоростей, ускорений).
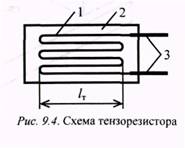
Тензорезистор (рис. 9.4) представляет собой плоскую петлеобразную спираль 1 из тонкой (0,01...0,03 мм) константановой (60 % меди и 40 % никеля) проволоки, вклеенной между двумя слоями рисовой бумаги 2. Рабочий тензорезистор наклеивается (клей БФ) на деталь и при ее нагружении деформируется совместно. При статическом нагружении рабочие тензорезисторы подключаются к измерителю деформации (цифровому) ИДЦ, электрическая схема которого (рис. 9.5) представляет собой высокочувстви-тельный измерительный четырехплечий мост Ч.Уитстона(1844).
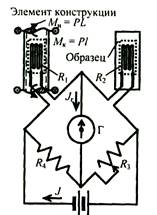
Рис. 9.5. Электрическая схема ИДЦ
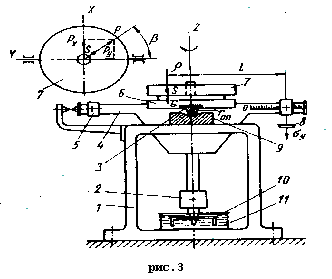
Постановка работы. На экспериментальной установке (рис. 9.6) проведены испытания ЭК в виде стальной (Е = 2 * 105 МПа; µ = 0,3) трубы (D = 60 мм; d= 54 мм; L = 360 мм; l = 300 мм) при плоском изгибе, кручении и совместном изгибе с кручением с записью (табл. 9.3) ступеней рабочей нагрузки Р и показаний т измерителя деформаций цифрового ИДЦ (цена деления β= 10-5 1/дел.).
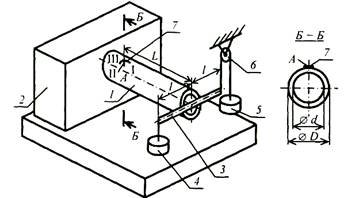
Рис. 9.6. Схема экспериментальной установки: 1- элемент конструкции; 2 - опора; 3 - коромысло; 4, 5 - грузы; 6 -блок; 7-прямоугольная розетка тензорезисторов; I, II, III - рабочие тензорезисторы
| №ступени нагружения | Р, кН | ΔР, кН | Изгиб | Кручение | Изгиб с кручением | |||||||
| m1 | Δm1 | m11 | Δm11 | m1 | Δm1 | m11 | Δm11 | m111 | Δm111 | |||
| 0 | 0.9 | - | 23 | - | 25 | - | 22 | - | 20 | - | -7 | - |
| 1 | 1.8 | 0.9 | 45 | 22 | 49 | 24 | 45 | 23 | 39 | 19 | -14 | -7 |
| 2 | 2.7 | 0.9 | 67 | 22 | 74 | 25 | 67 | 22 | 61 | 22 | -22 | -8 |
| 3 | 3.6 | 0.9 | 89 | 22 | 99 | 25 | 89 | 22 | 81 | 20 | -28 | -6 |
| 4 | 4.5 | 0.9 | 113 | 24 | 124 | 25 | 111 | 22 | 100 | 19 | -34 | -6 |
|
| ΔPср=0,9 | Δm1ср=22,5 | Δm11ср=24,75 | Δm1ср=22,25 | Δm11ср=20 | Δm111ср=-6,75 | ||||||
Требуется: определить расчетные и экспериментальные значения напряжений; вычислить отклонения расчетных от экспериментальных напряжений.
Проводим обработку экспериментальных данных табл. 9.3 и определяем
средние значения приращений нагрузки ΔPср =∑ΔР/4 и показаний ИДЦ:
Δmср =∑Δm/4.
В дальнейшем все расчеты проводятся для одной ступени нагружения.
Опыт № 1. Определение напряжений при изгибе элемента конструкции
1. Вычисляем расчетное приращение напряжений в точке А при изгибе:
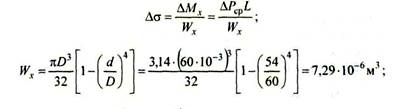
Δσ = ![]()
2. Рабочий тензорезистор I наклеен по направлению главной деформации Δε1, и находится в условиях линейного напряженного состояния. Определяем экспериментальные приращения главной деформации и главного напряжения:
Δε1э=Δ1срβ=22,2*10-5; Δσэ=EΔε1э=2*10-5=45 Мпа
3. Находим отклонение расчетных от эксперементальных напряжений:
δ=![]() *100%=44,4*45/45*100%= -1,33
*100%=44,4*45/45*100%= -1,33
4. Для оценки прочности элемента конструкции определяем экспериментальное значение напряжений при максимальной нагрузке:
maxσэ= ΔσэPmax/ΔP=45*4.5/0.9=255МПа
Опыт № 2. Определение напряжений при кручении элемента конструкции
1. Вычисляем расчетные приращения касательных напряжений в точке А:
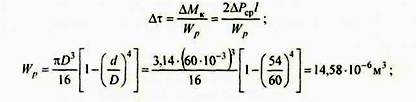
Δτ =(2*0,9*103*300*10-3)/14,58*10-6=37 МПа
2. При кручении элемента конструкции реализуется частный случай плоского напряженного состояния, когда главная деформация Δε1э = - Δε3э. Главную деформацию Δε1 измеряет рабочий тензорезистор II, наклеенный под углом 45◦. Определяем экспериментальные приращения главных деформаций:
Δε1э= Δm11cрβ=24,75*10-5; Δε3э=-24,75
3. Находим экспериментальные приращения касательных напряжений, которые при кручении равны приращениям главных напряжений:
![]()
Δτэ=(2*105\1+0.3)*24,75*10-5=38 МПа
4. Определяем отклонение расчетных от экспериментальных напряжений:
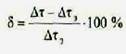
δ=((37-38)/38)*100%=-2,63
5. Для оценки прочности при кручении элемента конструкции находим экспериментальное значение касательных напряжений при максимальной нагрузке:
![]()
maxτэmax=38*4,5/0,9=190 МПа.
Опыт № 3. Определение напряжений при совместном изгибе и кручении элемента конструкции
1. Вычисляем расчетные приращения нормальных, касательных, главных и эквивалентных напряжений в точке А:
![]()
Δσ = (0,9*103*360*10-3)/7,29*10-6=44,4 МПа
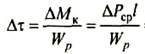
Δτ = (0,9*103*300*10-3)/14,58*10-6=18,5 МПа
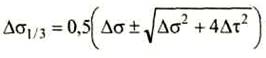
Δσ1/3=0,5(44,4![]() )=(22,2
)=(22,2![]() 28,9) МПа
28,9) МПа
Δσ1=51,1МПа ; Δσ3= -6,7 МПа
Их направление t
g2α=![]() = -
= -![]() =-0.833; 2α0=-39,8◦; α0=-19,9◦
=-0.833; 2α0=-39,8◦; α0=-19,9◦
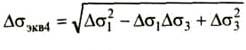
Δσэкв4=![]() =54,8 МПа
=54,8 МПа
2. По трем показаниям ИДЦ прямоугольной розетки тензорезисторов ходим эксперимен-тальные приращения деформаций:
Δε1э=Δm1 срβ=22,25*10-5 ; Δε11э = Δm1 1срβ = 20*10-5; Δε111э= Δm11 1срβ=-6,75
3. Вычисляем экспериментальные приращения главных деформаций и их направление:
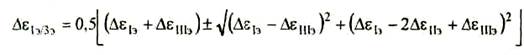
Δε1/3э=0,5(22,25*10-5+(6,75)*
*10-5![]() 2=7,75*10-5
2=7,75*10-5![]() 18,98*10-5
18,98*10-5
Δε1э=26,73*10-5 ; Δε3э=-11,23*10-5
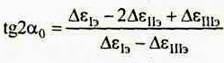
tg2α=(22.25 *10-5-2*20*10-5+(-6.75*10-5)/22.25*10-5-(-6.75*10-5)=-0.844
С учетом этого 2α0=-40,2◦ ; α0=-20,1◦
4. Определяем экспериментальные приращения главных и эквивалентных напряжений:
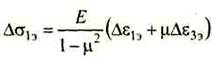
Δσ1э=51,3 МПа
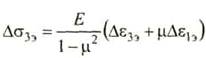
Δσ3э=-7,12
![]()
Δσэкв4=55,2МПа
5. Вычисляем отклонение расчетных от экспериментальных эквивалентных напряжений:
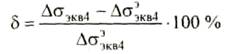
δ=((54,8-55,2)/55,2)*100%=-0,7%
6. Для оценки прочности элемента конструкции находим экспериментальные эквивалентные напряжения при максимальной нагрузке:
maxσээкв4=55,2*4,5/0,9=276МПа
Выводы
1. Изучена методика определения напряжений электротензометрированием с целью экспериментальной оценки прочности элементов конструкций.
1.Во всех трех опытах отклонения результатов расчета от эксперимента не превышают 5 %. Следовательно, электротензометрирование может эффективно использоваться для экспериментального определения напряжений при оценке прочности элементов конструкций.
2.Расхождения между расчетными и экспериментальными напряжения ми обусловлены рядом принимаемых гипотез при выводе формул для расчета напряжений, а также погрешностями измерения деформаций при электротензометрировании.
Похожие работы
... вызовет динамические давления на подшипники А и В, равные соответственно (рис.2) QA= P1 a + L / L = P1 85 + 340 / 340 » 1,25P1 ; (8) QB = - P1 a / L = - P1 85 / 340 » - 0,25P1 . Если предположить, что статическая балансировка ротора будет выполнена абсолютно точно путем прикрепления корректирующей массы в плоскости балансировочного кольца, то тогда динамическое давления на подшипники ротора ...
... -автомат с тепловым реле шт. 3 50,00 150,00 итого: 1450,00 Суммарные затраты 1769,58 При эксплуатации установки потребляется 5 кВтЧч электроэнергии, что составит 98 рублей. Установка для статической балансировки является исключительно лабораторным стендом и использоваться в качестве промышленной установки не может. Норма расходов на содержание ...





0 комментариев