Использование обобщений при обучении математике в средней школе

Курсовая работа по теме

"Эстетическое воспитание школьников в процессе обучения математике".

I. Цели обучения и воспитания в средней школе

В методической литературе уже много лет идут дискуссии по вопросам приоритета в паре "цели обучения - содержание" и корректности описания целей. Все недоумения, возникающие при этом, объясняются тем, что в анализе взаимодействия целей и содержания и обучения есть несколько уровней:

·  уровень теоретического представления математического образования;

·  уровень учебного предмета математики;

·  уровень учебных материалов;

·  уровень реального учебного процесса.

На первом уровне цели обучения могут быть сформулированы в общем виде, на этом уровне они определяют предметное содержание обучения.

Как правило, в большинстве учебных пособий по методике преподавания математике выделяют три группы целей обучения: общеобразовательные, воспитательные и практические.

Первая группа целей включает: овладение системой математических знаний, умений и навыков, дающей представление о предмете математике, ее языке и символике, математическом моделировании, специальных математических приемах, алгоритме, периодах развития математики.

Вторую группу целей обучения составляют: формирование мировоззрения учащихся, формирование логической и эвристической составляющих мышления, формирование алгоритмического мышления, приобщение к творческой деятельности, воспитание нравственности, культуры общения, самостоятельности, активности, эстетического воспитания школьников, воспитание трудолюбия.

Ясно, что каждая из целей этой группы может быть представлена более конкретно. Например, логическая составляющая мышления включает понимание структуры определения понятия, умение оперировать определение (выяснить принадлежность объекта понятию, выводить следствия из факта принадлежности к понятию, используя определение, конструировать объекты, относящиеся к объему понятия), умение классифицировать понятия, умение конструировать новые понятия, понимание логической структуры теоремы, понимание сущности доказательства, владение приемами опровержения предложенных обоснований и т.д. Конкретизация отдельных составляющих целей обучения важна для построения совокупностей целей урока, адекватной предметному содержанию учебного материала. Трансформация целей обучения математике в действия позволит осуществить диагностику и управление процессом усвоения знаний, умений школьников, их развитием и воспитанием.

К практическим целям обучения математике отнесем: формирование умений строить математические модели простейших реальных явлений, исследовать явления по заданным моделям, конструировать приложения моделей, ознакомление с ролью математики в научно-техническом прогрессе, современном производстве.

Перечисленные цели обучения математике отражают первый уровень анализа целей, т.е. уровень теоретического представления математического образования. (Перечисленные цели можно считать целями математического образования.) Они составляют основу отбора содержания, адекватного им. Оно охватывает линии расширения понятия числа, уравнений и неравенств, функций, элементов математического анализа, элементов теории вероятностей и статистики, приложений математики, геометрических преобразований, векторов, координат, элементов математической логики, аксиоматического метода. В содержании математического образования, кроме предметных знаний, должны быть включены действия, адекватные математическим понятиям, теоремам, общенаучные методы познания, а также специальные эвристические приемы.

На уровне учебного предмета цели обучения математике будут почти совпадать с перечисленными целями математического образования. Первая группа целей обучения будет заключаться в обеспечении овладением системой математических знаний и способов деятельности, эвристик, методов, составляющих содержание математического образования. Вторая и третья группа целей обучения совпадают с соответствующими целями математического образования. Возможно все эти цели представить в более конкретной форме, разложив способы деятельности на составляющие. На уровне учебника математики цели обучения соотносятся со спецификой курса и задаются в форме знаний, умений или в какой-либо другой форме. Так, например, программа по математике для образовательных учреждений фиксирует следующие цели изучения курса геометрии в VII-IX классах: систематическое изучение геометрических фигур на плоскости, формирование пространственных представлений, развитее логического мышления и подготовка аппарата, необходимого для изучения смежных дисциплин и курса стереометрии в старших классах. На уровне учебника цели обучения формулируются с учетом содержания учебного материала, а также требований к подготовке учащихся, определяемых стандартом среднего математического образования. На уровне учебника цели обучения формулируются уже с учетом особенностей учащихся класса, возможностей дифференциации обучения.

Известны различные способы постановки целей обучения:

o  определение целей через изучаемое содержание;

o  определение целей через деятельность учителя;

o  постановка целей через внутренние процессы интеллектуального, эмоционального, личностного и т.п. развития ученика;

o  постановка целей через учебную деятельность учащихся.

Наиболее популярной является система учебных целей, разработанная Б. Блумом. В технологии Б. Блума выделяется шесть уровней изучения учебного материала: знание, понимание, применение, анализ, синтез, оценка.

Категория "знание" обозначает запоминание и воспроизведение изученного материала. Показателем способности понимать может служить преобразование материала из одной формы выражения в другую, "перевод" его с одного языка на другой (например, из словесной формы в математическую). В качестве показателя понимания может также выступать интерпретация учеником (объяснение, краткое изложение) или предположение о дальнейшем ходе явлений, событий, предсказание последствий, результатов. Категория "применение" обозначает умение использовать изученный материал в конкретных условиях и новых ситуациях. Категория анализа обозначает умение разбить материал на составляющие так, чтобы ясно выступала его структура. Сюда относится вычисление частей целого, выявление взаимосвязей между ними, осознание принципов организации целого. Учебные результаты характеризуются при этом более интеллектуальным уровнем, чем понимание и применение, поскольку требует осознания как содержания учебного материала, так и его внутреннего строения. Категорией "синтез" обозначается умение комбинировать элементы, чтобы получить целое, обладающее новизной. Таким новым продуктом может быть план действий или совокупность обобщенных связей. Соответствующие учебные результаты могут быть получены в процессе деятельности творческого характера с акцентом на сознание новых схем и структур. Категория оценки обозначает умение оценивать значение того или иного материала для конкретной цели. Суждения ученика должны основываться на четких критериях, которые могут определяться самим учеником или задаваться извне.

Среди целей преподавания математики в школе можно выделить еще одну - формирование у учащихся представлений о математике как части общечеловеческой культуры. Учителя математики часто считают ее не главной и не уделяют должного внимания соответствующей работе на уроке. Практика работы с историей математики показывает, что именно при помощи истории науки, которая методически правильно включена в урок, достигается вышеуказанная цель.

 

II. Эстетическое воспитание в процессе обучения

О роли и значении уроков математики в воспитании правильного и дисциплинированного мышления говорилось и писалось очень много. Напротив, о влиянии математических знаний на эстетическое формирование личности учащегося не сказано почти ничего. Всегда предполагалось, что по абстрактности своего предмета математическая наука не может давать учащимся тех непосредственных впечатлений, эстетически воздействующих и формирующих характер образов, картин, эмоций, какими располагает история и литература. А.Г. Мордкович сформулировал мысль: " Математика - это самая главная гуманитарная наука, которая позволяет упорядочить свои мысли, разложить по полочкам нужную информацию". Математика единственный предмет, который учит учащихся систематизации мышления, точности излагаемого, яркости определения. Действительно, какой другой предмет научит учеников кратко, но точно излагать свою мысль, достоверно передавать описание того или иного предмета. Именно на математике мы применяем такой опыт, как запись условия задачи математическим языком.

Глубокая и важная черта математических заданий состоит в присущем им в значительном большинстве случаев творческом характере. В то время как в большинстве других областей знания выполнение задания, за немногими исключениями, требует от учащегося лишь определенных знаний и навыков - в лучшем случае еще умение стройно и стилистически излагать эти знания, - решение математической задачи, как правило, предполагает изобретение специально ведущего к поставленной цели рассуждения и тем самым становиться - пусть весьма скромным - творческим актом. Именно этот творческий, исследовательский характер математических заданий более чем что-либо другое влечет к себе молодые силы растущего и крепнущего интеллекта учащегося. Тот, кто изведал благородную радость творческого достижения, никогда уже не пожалеет усилий, чтобы вновь ее испытать.

Математика в отличие от большинства других преподаваемых в школе дисциплин имеет предметом своего обучения не непосредственно вещи, составляющий нас окружающий мир, а количественные отношения и пространственные формы, свойственные этим вещам.

Математика владеет не только истиной, но и высшей красотой-красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства. (Б. Рассел)

Таким образом, в математике как ни в какой другой науке находит выражение важнейший критерий научной красоты - единство в многообразии. Математика раскрывает перед человеком красоту внутренних связей, существующих в природе, и указывает на внутреннее единство мира.

Язык математики - это особый язык науки. В отличии от естественного языка, который в основном классифицирует предметы и потому является языком качественным, язык математики прежде всего количественный. Количественный язык представляет собой дальнейшее развитие и уточнение обычного качественного языка.

Важнейшим преимуществом количественного языка математики является краткость и точность. В этом его огромное преимущество и в этом его красота, ибо именно в математическом языке претворяется один из основных признаков красоты в науке: сведение сложности к простоте.

Итак, математика - это не только самостоятельная наука о “математических структурах”, но и язык других наук, язык единый, универсальный, точный, простой и красивый. Хорошо сказал об этих качествах математики советский математик С.Л. Соболев: “Есть одна наука, без которой невозможна никакая другая. Это математика. Ее понятия, представления и символы служат языком, на котором говорят, пишут и думают другие науки. Она объясняет закономерности сложных явлений, сводя их к простым, элементарным явлениям природы. Она предсказывает и предвычисляет далеко вперед с огромной точностью ход вещей. ”

Что можно рассматривать на уроках математики, предвещающих красоту, стройность, закономерность? И как это связать с искусством и живописью?

Симметрия является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство. (Г. Вейгель)

Т.О., симметрия воспринимается человеком как проявление закономерности, порядка, царящего в природе. Итак, целесообразность симметрических форм была осознана человечеством в доисторические времена, а в сознании древних греков симметрия стала олицетворением закономерности, целесообразности, а следовательно и красоты.

Пушкин А.С. рисует величавую Царевну - Лебедь со звездой во лбу (красота - симметрия) и окривевших злодеек ткачиху с поварихой (уродство - асимметрия).

Пропорция в искусстве определяет соотношение величин элементов художественного произведения. В эстетике пропорция, как и симметрия, является составным элементом категории меры и выражает закономерность структуры эстетического образа.

Возьмем простой пример: деление отрезка прямой. Если отрезок разделить пополам, зеркально - симметрично, то такое деление выглядит уравновешенным, мертвым. Если же точку деления взять слишком близко к одному из концов отрезка, то новая конфигурация будет чересчур неуравновешенной. Только некоторая “золотая середина”, которая не является геометрической серединой, обеспечивает желаемое единство симметрии и асимметрии.

Такое “радующее глаз” деление отрезка, по преданию, было известно еще Пифагору и называлось им “золотой пропорцией”. У древних египтян, “золотая пропорция" определяется как деление отрезка на две неравные части, при котором меньшая из них так относится к большей, как последняя ко всей длине отрезка. Художник и инженер Леонардо да Винчи называл ее “Sectio aurea" (золотое сечение), а математик и астроном Иоганн Кеплер, обнаруживший “золотую пропорцию" в ботанике, называл ее “Sectio divina” (божественное сечение).

“Золотое сечение" мы находим всюду: в изобразительном и прикладном искусстве, в архитектуре и музыке, в литературе, в предметах быта и машинах.

Каждому человеку нужно знать, какими были и как жили его давние и недавние предки, что довелось испытать и пережить народам нашей Родины на протяжении прошедших веков.

Что же это за наследие?

Это летописи, сказания, жития святых и праведников, песни и легенды. Это документы общественной жизни и становление российской государственности: законы, нравственные заповеди, указы и гражданские акты, договоры царей князей и других правителей.

Это творения художников, запечатлевших былые картины природы, панорамы городов, сцены быта, обряды и занятия наших пращуров.

Это сбереженные в музеях орудия труда, утварь, одежда, игрушки, разнообразные изделия искусных умельцев - мастеров.

Это памятники архитектуры - от церквей, монастырей и крепостей до мельниц, хозяйственных построек.

Погрузиться в прошлое, реально представить его картины и вместе с тем как бы стать участником былых событий нам поможет математика.

В развитии восприятия, внимания, памяти, произвольности мышления огромную лепту вносит оригами - искусство, близкое ребенку и доступное.

Не перечислить всех достоинств оригами в развитии ребенка. Доступность бумаги как материала, простота ее обработки привлекают учеников. Они овладевают различными приемами и способами действий с бумагой, такими, как сгибание, многократное складывание, надрезание, склеивание.

Оригами развивает у учащихся способность работать руками под контролем сознания, происходит развитие глазомера.

Оригами способствует концентрации внимания, так как заставляет сосредоточиться на процессе изготовления, чтобы получить желаемый результат.

Оригами имеет огромное значение в развитии конструктивного мышления детей, их творческого воображения, художественного вкуса, стимулирует развитие памяти, так как ребенок должен запомнить последовательность ее изготовления.

Оригами способствует четкому запоминанию таких геометрических понятий, как угол, сторона, квадрат, треугольник и т.д.

Оригами активизирует мыслительные процессы. В процессе конструирования у учащегося возникает необходимость соотнесения наглядных символов (показ приемов складывания) со словесными (объяснение приемов складывания) и перевод их значения в практическую деятельность (самостоятельное выполнение действий).

Оригами совершенствует трудовые умения учащегося, формирует культуру труда.

Этапы техники оригами.

1.  Учитель объясняет приемы складывания и показывает на своем образце - учащиеся повторяют действия.

2.  Учитель объясняет приемы складывания, опираясь на схемы, - учащиеся выполняют.

3.  Учитель чертит схемы, не объясняя приемов складывания, - учащиеся выполняют.

4.  Учитель предлагает нарисовать схемы складывания базовых форм.

5.  Учитель называет базовые формы - учащиеся самостоятельно складывают.

6.  Учащиеся самостоятельно объясняют схемы складывания.

7.  Учащиеся самостоятельно объясняют и показывают приемы складывания.

Большую роль в эстетическом воспитании играет умение учеников чертить плоскостные фигуры, путем подбора выпуклых фигур комбинировать небольшие мозаичные фрагменты.

Представьте себе, что у вас имеется неограниченный запас одинаковых по форме деталей. Если ими можно покрыть всю плоскость без зазоров и наложений, то о таких фигурах говорят, что ими можно вымостить, или выложить, плоскость, а плоскость, выраженную фигурами, называют мозаикой. С древнейших времен такие мозаики использовались во всем мире для украшения полов, стен, в узорах для мебели, ковров, обоев, одежды и др. предметов.

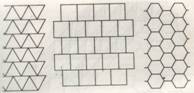
Голландский художник М.К. Эшер с необычайной изобретательностью покрывал плоскость фигурами сложной конфигурации, напоминающими своими очертаниями птиц, рыб, животных и др. живых существ.

Наиболее ярким примером обладает анаморфное изображение фрагментов рисунка.

Этот термин происходит от греческих ana - снова и morphe - форма и означает реалистическое изображение, настолько сильно деформированное проективным преобразованием, что оно становится трудноузнаваемым. Если такую картинку рассматривать под некоторым углом к его плоскости, то появление неискаженного изображения столь неожиданно, что те, кто наблюдает подобный эффект впервые, как правило, вскрикивают от удивления.

Наиболее известным примером анаморфного изображения служит фрагмент картины Ханса Хольбейна “ Испанские послы" (1533г.).

Зажмурив один глаз и наклоняя страницу с репродукцией картины от себя так, чтобы левый нижний угол ее был направлен в открытый глаз и находился на расстоянии около 15 см, можно увидеть у ног послов череп.

Другой яркий пример анаморфного изображения можно наблюдать в загадочной картинке Сэма Ллойда.

В ней “запрятан" портрет Джорджа Вашингтона в зрелые годы. На этой же картинке изображена головоломка Сема Лойда: квадратный пирог Вашингтона требуется разрезать на 6 квадратных кусков не обязательно одинаковых размеров. “Косые изображения" такого рода иногда встречаются в детских книжках и рекламных объявлениях.

Этот метод анаморфного изображения иногда используется в дорожных знаках: слово “СТОП" располагается под таким углом, что его в нормальном ракурсе видит только водитель, приближающийся к перекрестку.

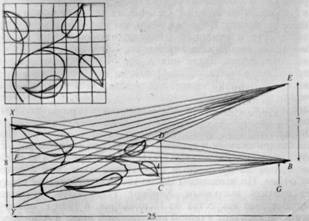
Геометрический метод построения косых изображений состоит в том, что сначала картину расчерчивают на квадратные клетки, затем матрицу растягивают, превращая ее в трапецию, после чего художник копирует картину, заполняя трапециевидные клетки и тщательно следя за возможно более точным соответствием содержимого каждой растянутой клетки содержимому квадратного оригинала.

Составление картинок из 7 кусочков дерева, известных под названием ТАНОВ - одно из самых древних развлечений на Востоке. Таны имеют простейшую форму, но позволяют составлять бесконечно много разнообразнейших фигурок - танграмов. Составление таких фигурок предъявляет весьма высокие требования к геометрической интуиции, развивает образное мышление, художественные способности играющего.

Что такое таны? Несколько тысяч лет тому назад китайский ученый очень остроумно разрезал квадрат на 7 частей.

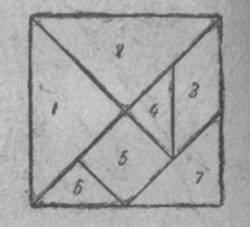
Игра в танграм распадается на три основные категории:

1.  Поиск одного или нескольких способов построения данной фигурки или изящного доказательства невозможности построения фигурки;

2.  Нахождения способа, позволяющего с наибольшей выразительностью или юмором (или тем и другим вместе) изобразить силуэты животных, людей и другие узнаваемые предметы;

3.  Решение различных задач комбинаторной геометрии, возникающих в связи с составлением фигур из 7 танов.

Чем полезна эта игра, что она дает учащимся? Во-первых, ученики воочию убеждаются, что подобие и равенство фигур - это не одно и тоже, знакомятся со всеми свойствами фигур. Во-вторых, развивается образное мышление и полет фантазии.

Еще о чем полезном можно и нужном на уроках математики говорить? О чем угодно, обо всем, что используем на уроке: циркуль, линейка, ластик, тетрадь.

Циркуль.

Возьмите в руки циркуль и внимательно его рассмотрите. Какой это красивый и необычный инструмент. Он очень похож на маленького длинноногого человечка. Этот волшебник умеет изображать окружность.

“Сговорились две ноги делать дуги и круги" - это загадка про циркуль, который нужен сегодня ученым, инженерам, учителям, студентам и школьникам. Оказывается, циркуль - древний инструмент. Название свое он получил от латинского слова циркулюс, что значит круг, окружность. Древнейшие циркули находят среди развалин старейших городов. Например, циркули с железными ножками были обнаружены среди пепла, что засыпал 1800 лет назад древнеримский город Помпею. О том, что человек пользуется циркулем очень давно, свидетельствуют рисунки с изображением ровных, правильных окружностей на храмах, куполах домов, посуде.

В настоящее время существует множество различных циркулей. Самый простой наш помощник - одноногий циркуль, который имеет смешное название козья ножка.

Циркуль - измеритель очень похож на обычный, только обе его ноги имеют иголочки. Такой циркуль нужен для проведения точных измерений. Есть циркули большие, например штангенциркуль, который помогает инженерам проводить огромные окружности.

Линейка.

Было время, когда длину измеряли веревочкой, величиной ступни (фут, пядь), длиной пальцев (дюйм), величиной локтя (ярд), саженью (расстояние от подошвы левой ноги до кончиков пальцев поднятой вверх правой руки, наискосок). Все измерения при этом, конечно, были приблизительными. С 1791 года люди многих стран условились считать метром одну десятимиллионную часть от четверти длины того меридиана, который проходит через город Париж. Само слово метр произошло от греческого мера - точная мера длины. Тогда же был выполнен образец метра - узкая тонкая линейка из драгоценного металла, который называется платиной.

У обычной линейки много родственников. Ее брат угольник состоит из целой семейки линеек - папы, мамы и ребенка, соединенных в виде треугольника.

Большая линейка в виде буквы “Т” называется рейсшиной. Маленькой частью она упирается в край чертежной доски, а длинной ножкой - линейкой двигается по листу бумаги. Такая линейка незаменимая помощница любого конструктора и чертежника. Линии, которые выполняют с ее помощью, будут параллельны друг другу.

Для измерения в столярных работах используется складной метр - метровая линейка, которую складывают для удобства и хранения. Для этих же целей служит рулетка - линейка из тонкого металла, свернутого рулоном, который спрятан в специальной коробочке.

Ластик.

Без этого приспособления не обойдется никто. От начинающего впервые рисовать малыша до профессионала - все пользуется резинкой для стирания. Не забывайте и вы аккуратно удалять неточности на рисунках и чертежах. Да, смотрите, не перестарайтесь! Ведь если вы будете пользоваться ластиком с силой, то на бумажном листе может образоваться самая обыкновенная дырка. После этого говорить о красоте вашей будущей работы уже не стоит, она испорчена! Вот такой непростой этот маленький инструмент для стирания!

Способность человека быть творцом воспитывается прежде всего в школе. Уже простое самостоятельное решение задач по математике - работа творческая, но это лишь начальная ступень развития творческих сил и способностей человека, начальная стадия эстетической зрелости. Дальнейшие шаги по этому пути - умение самому поставить вопрос, самому сконструировать задачу. А что такое творческие способности и эстетический подход? Четкого ответа на этот вопрос психология не дает. Практика показывает: если школьник проявляет большой интерес к математике, если он с успехом, а часто и с удовольствием решает трудные математические задачи, то с большей уверенностью можно предположить, что у этого школьника имеются не только математические способности, но и ясность в мышлении, порядок в логике.

 

III. Эстетический потенциал математики как науки

Эстетический потенциал математики в практике обучения часто недооценивают. Однако на протяжении веков пути математики и различных видов искусства переплетались.

Поэтому исторические сведения предоставляют благодатный материал для развития эстетического вкуса школьников. Зачастую в кругу цифр и математических знаков мы не замечаем всей красоты и логичности доказательств этой науки. Красоту науки когда-то заметил Н.Е. Жуковский. Он писал: "В математике есть своя красота, как в живописи и в поэзии".

Многие ученые, занимавшиеся исследованиями в области математики, были не только математиками, но физиками и химиками, как Ньютон, Паскаль и Эйлер, и даже поэтами. Философом и поэтом является известный математик Омар Хайям.

Вот одно из его четверостиший:

Чтоб мудро жизнь прожить, знать надобно немало.

Два важных правила запомни для начала:

Ты лучше голодай, чем что попало ешь,

И лучше будь один, чем вместе с кем попало.

Другой пример - математик Чарльз Л. Доджсон, известный больше под псевдонимом Льюис Кэрролл как автор сказки "Алиса в стране чудес".

Как рассказывают биографы, королева Виктория пришла в восторг от этой книги и захотела прочитать все книги, написанные Кэрроллом.

Можно представить ее разочарование, когда она увидела на своем столе стопку книг по математике. И даже известная нам математик-женщина Софья Васильевна Ковалевская обладала незаурядным литературным талантом. Ее перу принадлежат такие произведения: драма "Борьба за счастье", роман "Нигилистка" и другие.

Решать уравнение вида: х-ау=1, по-видимому, умел и Архимед, находим мы в книге Н.Я. Виленкина. Недаром Архимед послал в Александрию Эратосфену следующий стихотворный вызов:

Сколько у Солнца быков, найди для меня, чужестранец

(Ты их, подумав, сосчитай, мудрости если не чужд),

Как на полях Тринакрийской Сицилии острова тучных

Их в четырех стадах много когда-то паслось.

Цветом стада различались: блистало много млечно-белым,

Темной морской волны стада другого был цвет.

Рыжим третье было, последнее пестрым. И в каждом

Стаде была самцов множеством тяжкая мощь,

Все же храня соразмерность такую: представь чужестранец,

Белых быков в точности было ровно…

То, что древние математики были прекрасными поэтами, можно видеть из приведенных примеров. Эти произведения помогут показать ученикам красоту не только самой математики, но и поэзии, прозы и других древних сочинений. При этом исторические сведения помогут сосредоточить и сконцентрировать внимание учащихся на изучении программного материала, помогут надолго сохранить в памяти те факты, которые были красиво описаны с помощью литературы.

В стихах, приведенных выше, также встречаются географические названия: Александрия, Тринакрийская Сицилия и другие. При сообщении учащимся исторических сведений, если учитель приведет карты древние и современные, то ученики наиболее полно представят себе картину времени, когда произошло математическое открытие. При рассмотрении карт ученики могут найти древние города, например, город Александрию, и затем ответить на вопросы: каким морем омывается город? (Средиземным); с какой рекой связаны истории этого города?; к какой стране принадлежит Александрия? (Египет); назвать главную реку Египта и ее природные особенности? (Нил); перечислить известных людей, проживавших в Александрии? (Евклид, Эратосфен, Апполоний, Герон, Гиппарх, Птолемей, Диофант). Такая работа позволяет развивать воображение, мышление учащихся и тем более поможет лучше разобраться в географических местах и надолго отложиться в памяти детей, так как эти знания были добыты путем сопоставления карт. Приведенный в примерах Диофант занимался изучением методов решения уравнений. Уравнения, решаемые в целых числах так и назвали Диофантовыми уравнениями. А также с его именем связаны понятия Ал-джебра и Ал-мукабала.

Ал-джебра

При решении уравненья,

Если в части одной,

Безразлично какой,

Встретится член отрицательный,

Мы к обеим частям,

С этим членом сличив,

Равный член придадим,

Только с знаком другим,

И найдем результат нам желательный.

Ал-мукалаба

Дальше смотрим в уравненье,

Можно ль сделать приведенье,

Если члены в нем подобны,

Сопоставить их удобно,

Вычтя равный член из них,

К одному приводим их.

После изучения подобных стихов можно выводить современные методы решения линейных уравнений: перенос слагаемых их одной части уравнения в другую, деление и умножение обеих частей уравнения на одно и то же число.

Исследования Н.Я. Виленкина в области истории науки математики, показывают, что математикой занимались не только профессионалы. Эта наука притягивала внимание многих людей. Так, например, в "Маленьком принце", замечательной сказке французского писателя А. Де Сент-Экзюпери, Лис спрашивает Маленького принца:

А на той планете есть охотники?

Нет.

Как интересно! А куры есть?

Нет.

Нет в мире совершенства! - вздыхает Лис.

Н.Я. Виленкин предлагает поспорить о не существовании совершенства в мире и именно с этого литературного текста начать беседу о совершенных числах - числах, делители которых в сумме дают само число.

Опытный учитель с привлечением истории математики к объяснению нового материала сможет показать ученикам значимость математики среди других наук, изучаемых в школе, и их неразрывную связь. Из вышеуказанных примеров видно, что при использовании географических карт, литературных произведений, биографий ученых история математики позволяет установить межпредметные связи, которые очень легко можно проследить на каждом уроке.

При распаде СССР многие социалистические республики, отделившись, стали возвращаться к своим традициям и к родному языку. История математики может вернуть нас к истокам исконно русских открытий, познакомить с нашими отечественными учеными и с их вкладом в становление науки - математики. Известный историк-методист И.Я. Депман справедливо утверждает: "Исторические сведения о математике своей Родины и ее достижениях естественно развивают патриотические чувства и любовь в своей стране, к своему народу. Русская математика, как старая, так и новая, дает для этого очень богатые возможности". В изучении простых чисел учеников можно познакомить с отечественным ученым П.Л. Чебышевым, которому наравне с другими исследователями этих чисел удалось вывести формулу, позволяющую приближенно найти число простых чисел. Работа по исследованию простых чисел занимала умы ученых около 2200 лет после Евклида, и своим открытием П.Л. Чебышев прославил русскую науку.

Воспитание нравственности у подростков происходит под воздействием взаимоотношений людей, окружающих школьника, его сверстников, людей старшего и предшествующих поколений. Педагогический процесс всегда связан не только с учителями, но и с "явно не присутствующими учителями". В качестве авторитетных "отсутствующих учителей" успешно выступают различные выдающие личности, деятели науки и культуры, в том числе и ученые-математики. Исторический материал, действуя на сознание, на чувства и помыслы школьников, формирует их нравственные идеалы. Поэтому исторический материал обладает огромным потенциалом для патриотического и интернационального воспитания школьников. В интернациональном воспитании, в формировании уважения к народам нашей страны, видим у К.Г. Кожабаева, большое значение имеет ознакомление учащихся с достижениями великий ученых народов СССР, таких, как Хорезми, Омар Хайям, Насирэддин Туси, Гиясэддин Каши и других.

Неожиданные открытия, обнаруженные математиками, удивляли многие столетия людей своей красотой и вдохновляли на новые исследования. Говоря словами Г.В. Лейбница, "нет ничего более важного, как обнаружить источники нового открытия. Это, на мой взгляд, интереснее самих открытий". Мы еще раз убеждаемся в ценности элементов истории математики для развития учащихся. В этом случае учитель вместе с учениками может рассматривать новый материал, как никому раннее неизвестный, тем самым происходит новое открытие на уровне каждого ученика в отдельности.

Каждый год видим такую картину: от класса к классу интерес к изучению предмета математики у учащихся не возрастает, как хотелось бы, а наобо7рот, уменьшается, что влечет за собой и ухудшение успеваемости. Кроме воспитательного значения исторических сведений, учителя математики подчеркивают, что история математики повышает интерес учащихся к предмету, к изучению все новых и новых, усложняющихся тем программы. О развитии интереса к предмету при помощи истории математики говорить нужно много и основательно, поэтому мы не затронем в этой статье возникшей новой проблемы.

Из наблюдений за преподаванием истории математики в школе видим, что наиболее часто применяемыми методическими приемами сообщения исторических сведений являются следующие: рассказ учителя, эвристическая беседа, проблемное изложение, лекция, исследовательская работа учеников. Мы выделяем еще один прием, который заключается в решении той или иной задачи различными методами, не исключая существовавших ранее, может быть даже и ошибочных. А также прием выполнения одного математического действия различным образом. Например, при изучении темы умножения десятичных или обыкновенных дробей школьникам в 6 классе можно показать приемы умножения дробей старорусским и другими способами. Н.Н. Круликовский отмечает, что эффективным методом сообщения исторических сведений по математике может быть решение задач из классических и старинных сборников задач. При изучении признаков деления на 2, 3, 5, 10 и т.д. можно показать ученикам признак Паскаля. Затем можно будет сказать, что признаки делимости чисел на 2, 3, 5 и 10 - это частные случаи признака Паскаля.

Согласно Н.Н. Круликовскому, считаем, что ознакомление учащихся с элементами истории математики с целью воспитания должно проходить, прежде всего, на уроках математики. Многолетний опыт исследования данной темы показывает, что освещать историю математики даже в самом кратком виде не предоставляется возможным. Поэтому будем говорить только о сообщении учащимся лишь некоторых сведений из истории науки. Из нестандартным форм сообщения исторических ведений науки математики Н.Я. Виленкин выделяет уроки истории математики, которые проводятся в конце изучения каждой темы. Материал к этим урокам он располагает в учебнике в конце разделов.

Мы вводим в практику нетрадиционный прием сообщения сведений из истории математики - нетрадиционные домашние исследовательские задания. Почти исчезли из обихода русские старинные названия мер длины и веса. Ученики на лето обычно из крупных городов разъезжаются к родственникам, бабушкам и дедушкам, которые живут в деревнях, поселках и просто маленьких городках. Из их обихода эти устаревшие слова еще не вышли. За лето ученики могут выполнить специальное задание - составить словарь по старинным мерам длины по рассказам бабушек и дедушек. А во время урока по теме "Измерение отрезков" могут поделиться с остальными своими словарями и позабавить одноклассников различными интересными названиями, такими как сажень, вершок, аршин. Учитель в этом случае подтвердит сказанное школьниками и расскажет, чему в настоящее время равны эти величины. Интересно будет измерить кабинет математики пядями, локтями и шагами. А также исторический материал может стать индивидуальным средством обучения школьников математике.

Историю математики вводить в школу необходимо по нескольким причинам: это прекрасный и действенный инструмент для повышения интереса учащихся к предмету, развития эстетического вкуса учеников, а также привития нравственных качеств. Говоря словами Г.В. Лейбница, "кто хочет ограничиться настоящим без знания прошлого, тот никогда его не поймет", убеждаемся в этом еще раз. Главное, чтобы исторические сведения гармонично вписывались в современный урок - урок XXI века. XXI век - это век телевидения, компьютеров и компьютерных сетей. На первый план выходит научно-исследовательская деятельность учеников, которая должна привить им навыки самообразования.