"Длинная" арифметика
Известно, что арифметические действия, выполняемые компьютером в ограниченном числе разрядов, не всегда позволяют получить точный результат. Более того, мы ограничены размером (величиной) чисел, с которыми можем работать. А если нам необходимо выполнить арифметические действия над очень большими числами, например,
30! = 265252859812191058636308480000000?
В таких случаях мы сами должны позаботиться о представлении чисел в машине и о точном выполнении арифметических операций над ними.
Числа, для представления которых в стандартных компьютерных типах данных не хватает количества двоичных разрядов, называются "длинными". Реализация арифметических операций над такими "длинными" числами получила название "длинной арифметики".
Организация работы с "длинными" числами во многом зависит от того, как мы представим в компьютере эти числа. "Длинное" число можно записать, например, с помощью массива десятичных цифр, количество элементов в таком массиве равно количеству значащих цифр в "длинном" числе. Но если мы будем реализовывать арифметические операции над этим числом, то размер массива должен быть достаточным, чтобы разместить в нем и результат, например, умножения.
Существуют и другие представления "длинных" чисел. Рассмотрим одно из них. Представим наше число
30! = 265252859812191058636308480000000
в виде:
30! = 2 * (104)8 + 6525 * (104)7 + 2859 * (104) + 8121 * (104)5 + 9105 * (104)4 + 8636 * (104)3 + 3084 * (104)2 + 8000 * (104)1 + 0000 * (104)0.
Это представление наталкивает на мысль о массиве, представленном в табл. 1.
Таблица 1
| Номер элемента в массиве А | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Значение | 9 | 0 | 8000 | 3084 | 8636 | 9105 | 8121 | 2859 | 6525 | 2 |
Мы можем считать, что наше "длинное" число представлено в 10000-10 системе счисления (десятитысячно-десятичная система счисления, приведите аналогию с восьмерично-десятичной системой счисления), а "цифрами" числа являются четырехзначные числа.
Возникают вопросы. Что за 9 в А [0], почему число хранится "задом наперед"? Ответы очевидны, но подождем с преждевременными объяснениями. Ответы на вопросы будут ясны из текста.
Примечание. Мы работаем с положительными числами!
Первая задача. Ввести "длинное" число из файла. Решение задачи начнем с описания данных.
Const MaxDig = 1000; {Максимальное количество цифр — четырехзначных!}
Osn = 10000; {Основание нашей системы счисления,
в элементах массива храним четырехзначные числа}
Type Tlong = Array[0..MaxDig] Of Integer;
{Максимальное количество десятичных цифр в нашем числе}
Алгоритм ввода "длинного" числа из файла рассмотрим на конкретном примере.
Пусть в файле записано число 23851674 и основанием (Osn) является 1000 (храним по три цифры в элементе массива А). Изменение значений элементов массива А в процессе ввода (посимвольного в переменную Ch) отражено в табл. 2.
Таблица 2
| А[0] | А[1] | А[2] | А[3] | Ch | Примечание |
| 3 | 674 | 851 | 23 | - | Конечное состояние |
| 0 | 0 | 0 | 0 | 2 | Начальное состояние |
| 1 | 2 | 0 | 0 | 3 | 1-й шаг |
| 1 | 23 | 0 | 0 | 8 | 2-й шаг |
| 1 | 238 | 0 | 0 | 5 | 3-й шаг |
| 2 | 385 | 2 | 0 | 1 | 4-й шаг: старшая цифра элемента А [1] перешла в пока "пустой" элемент А[2] |
| 2 | 851 | 23 | 0 | 6 | 5-й шаг |
| 2 | 516 | 238 | 0 | 7 | 6-й шаг |
| 3 | 167 | 385 | 2 | 4 | 7-й шаг |
| 3 | 674 | 851 | 23 |
Проанализируем таблицу (и получим ответы на поставленные выше вопросы).
1. В А[0] храним количество задействованных (ненулевых) элементов массива А — это уже очевидно.
2. При обработке каждой очередной цифры входного числа старшая цифра элемента массива с номером i становится младшей цифрой числа в элементе i+1, а вводимая цифра будет младшей цифрой числа из А[1]. В результате работы нашего алгоритма мы получили число, записанное "задом наперед".
Примечание (методическое): Можно ограничиться этим объяснением и разработку процедуры вынести на самостоятельное задание. Можно продолжить объяснение. Например, выписать фрагмент текста процедуры перенос старшей цифры из A[i] в младшую цифру А[i+1], т.е. сдвиг уже введенной части числа на одну позицию вправо:
For i := A[0] DownTo 1 Do
Begin
A[i+l] := A[i+l] + (Longint(A[i]) * 10) Div Osn;
A[i] := (LongInt(A[i]) * 10) Mod Osn;
End;
Пусть мы вводим число 23851674 и первые 6 цифр уже разместили "задом наперед" в массиве А. В символьную переменную считали очередную цифру "длинного" числа — это "7". По нашему алгоритму эта цифра "7" должна быть размещена младшей цифрой в А[1]. Выписанный фрагмент программы "освобождает" место для этой цифры. В таблице отражены результаты работы этого фрагмента.
| i | А[1] | А[2] | А[3] | ch |
| 2 | 516 | 238 | 0 | 7 |
| 2 | 516 | 380 | 2 | |
| 1 | 160 | 385 | 2 |
После этого остается только добавить текущую (считанную в ch) цифру "длинного" числа к А[1] и изменить значение А[0].
В конечном итоге процедура должна иметь следующий вид:
Procedure ReadLong(Var A : Tlong);
Var ch : char; i : Integer;
Begin
FillChar(A, SizeOf(A), 0) ;
Read(ch);
While Not(ch In ['0'..'9']) Do Read(ch);
{пропуск не цифр во входном файле}
While ch In ['0'..'9'] Do
Begin
For i := A[0] DownTo 1 Do
Begin
{"протаскивание" старшей цифры в числе из A[i]
в младшую цифру числа из A[i+l]}
A[i+l] := A[i+l] + (LongInt(A[i]) * 10) Div Osn;
A[i] := (LongInt(A[i]) * 10) Mod Osn
End;
A[1] := A[l] + Ord(ch) - Ord('0');
{добавляем младшую цифру к числу из А[1]}
If A[A[0]+1] > 0 Then Inc(A[0]);
{изменяем длину, число задействованных элементов массива А}
Read(ch)
End
End;
Вторая задача. Вывод "длинного" числа в файл или на экран.
Казалось бы, нет проблем — выводи число за числом. Однако в силу выбранного нами представления "длинного" числа мы должны всегда помнить, что в каждом элементе массива хранится не последовательность цифр "длинного" числа, а значение числа, записанного этими цифрами. Пусть в элементах массива хранятся четырехзначные числа. Тогда "длинное" число 128400583274 будет в массиве А представлено следующим образом:
| A[0] | A[1] | A[2] | A[3] |
| 3 | 3274 | 58 | 1284 |
При выводе "длинного" числа из массива нам необходимо вывести 0058, иначе будет потеря цифр. Итак, незначащие нули также необходимо выводить. Процедура вывода имеет вид:
Procedure WriteLong(Const A : Tlong);
Var ls, s : String; i : Integer;
Begin
Str(Osn Div 10, Is);
Write(A[A[0]]; {выводим старшие цифры числа}
For i := A[0] - l DownTo 1 Do
Begin
Str(A[i], s);
While Length(s) < Length(Is) Do s := '0' + s;
{дополняем незначащими нулями}
Write(s)
End;
WriteLn
End;
Третья задача. Предварительная работа по описанию способа хранения, вводу и выводу "длинных" чисел выполнена.
У нас есть все необходимые "кирпичики", например, для написания программы сложения двух "длинных" положительных чисел. Исходные числа и результат храним в файлах. Назовем процедуру сложения SumLongTwo.
Тогда программа ввода двух "длинных" чисел и вывода результата их сложения будет иметь следующий вид:
Var A, B, C : Tlong;
Begin
Assign(Input, 'Input.txt'); Reset(Input);
ReadLong(A); ReadLong(B) ;
Close(Input);
SumLongTwo(A, B, C);
Assign(Output, 'Output.txt');
Rewrite(Output);
WriteLong(C);
Close(Output)
End.
Алгоритм процедуры сложения можно объяснить на простом примере. Пусть А=870613029451, В=3475912100517461.
| i | A[i] | B[i] | C[1] | C[2] | C[3] | C[4] |
| 1 | 9451 | 7461 | 6912 | 1 | 0 | 0 |
| 2 | 1302 | 51 | 6912 | 1354 | 0 | 0 |
| 3 | 8706 | 9121 | 6912 | 1354 | 7827 | 1 |
| 4 | 0 | 3475 | 6912 | 1354 | 7827 | 3476 |
Алгоритм имитирует привычное сложение столбиком, начиная с младших разрядов. И именно для простоты реализации арифметических операций над "длинными" числами используется машинное представление "задом наперед".
Результат: С = 3476782713546912.
Ниже приведен текст процедуры сложения двух "длинных" чисел.
Procedure SumLongTwo(A, B : Nlong; Var C : Tlong);
Var i, k : Integer;
Begin
FillChar(C, SizeOf (C), 0) ;
If A[0] > B[0] Then k := A[0] Else k : =B[0];
For i := l To k Do
Begin С [i+1] := (C[i] + A[i] + B[i]) Div Osn;
C[i] := (C[i] + A[i] + B[i]) Mod Osn
{Есть ли в этих операторах ошибка?}
End;
If C[k+l] = 0 Then C[0] := k Else C[0] := k + l
End;
Четвертая задача. Реализация операций сравнения для "длинных" чисел (А=В, А<В, А>В, А<=В, А>=В).
Function Eq(A, B : TLong) : Boolean;
Var i : Integer;
Begin
Eq := False;
If A[0] <> B[0] Then Exit
Else Begin
i := l;
While (i <= A[0]) And (A[i] = B[i]) Do Inc(i);
Eq := i = A[0] + l
End
End;
Реализация функции А > В также прозрачна.
Function More(A, B : Tlong) : Boolean;
Var i : Integer;
Begin If A[0] < B[0] Then More := False
Else If A[0] > B[0] Then More := True
Else Begin
i := A[0];
While (i > 0) And (A[i] = B[i]) Do Dec(i);
If i = 0 Then More := False
Else If A[i] > B[i] Then More := True
Else More:=False
End
End;
Остальные функции реализуются через функции Eq и More.
Function Less(A, B : Tlong) : Boolean; {A < B}
Begin
Less := Not(More(A, B) Or Eq(A, B))
End;
Function More_Eq(A, B : Tlong) : Boolean; {A >= B}
Begin
More_Eq := More(A, B) Or Eq(A, B)
End;
Function Less_Eq(A, B : Tlong) : Boolean; {A <= B}
Begin
Less_Eq := Not More(A, B)
End;
Для самостоятельного решения может быть предложена следующая, более сложная, задача. Требуется разработать функцию, которая выдает 0, если А больше В, 1, если А меньше В, и 2 при равенстве чисел. Но сравнение должно быть выполнено с учетом сдвига. О чем идет речь? Поясним на примере. Пусть А равно 56784, а В — 634. При сдвиге числа В на 2 позиции влево функция должна сказать, что В больше А, без сдвига, что А больше В. Другой пример. При А равном 56700, а В — 567 и сдвиге 2 функция должна "сказать", что числа равны. Решение может иметь следующий вид:
Function More(Const А, В : Tlong; Const sdvig : Integer) : Byte;
Var i : Integer;
Begin
If A[0] > B[0] + sdvig Then More := 0
Else
If A[0] < B[0] + sdvig Then More := l
Else Begin
i := A[0];
While (i > sdvig) And
(A[i] = B[i-sdvig]) Do Dec(i);
If i = sdvig Then Begin
More:=0;
{совпадение чисел с учетом сдвига}
For i := 1 To sdvig Do
If A[i] > 0 Then Exit;
More := 2;
{числа равны, "хвост" числа А равен нулю}
End
Else More := Byte(A[i] < B[i-sdvig])
End
End;
Пятая задача. Умножение длинного числа на короткое. Под коротким понимается целое число типа LongInt.
Процедура очень походит на процедуру сложения двух длинных чисел.
Procedure Mul(Const A : TLong; Const К : Longlnt; Var С : TLong);
Var i : Integer;
{результат - значение переменной С}
Begin
FillChar (С, SizeOf(С), 0);
If K = 0 Then Inc(С[0]){умножение на ноль}
Else Begin
For i:= l To A[0] Do
Begin
C[i+l] := (LongInt(A[i]) * K + C[i]) Div Osn;
C[i] := (LongInt(A[i])* K + C[i]) Mod Osn
End;
If C[A[0]+1] > 0 Then C[0]:= A[0] + 1
Else C[0]:= A[0]
{определяем длину результата}
End
End;
Шестая задача. Вычитание двух длинных чисел с учетом сдвига
Если понятие сдвига пока не понятно, то оставьте его в покое, на самом деле вычитание с учетом сдвига потребуется при реализации операции деления. В начале выясните логику работы процедуры при нулевом сдвиге.
Введем ограничение: число, из которого вычитают, больше числа, которое вычитается. Работать с "длинными" отрицательными числами мы не умеем.
Процедура была бы похожа на процедуры сложения и умножения, если бы не одно "но" — заимствование единицы из старшего разряда вместо переноса единицы в старший разряд. Например, в обычной системе счисления мы вычитаем 9 из 11 — идет заимствование 1 из разряда десятков, а если из 10000 вычитаем 9 — процесс заимствования несколько сложнее.
Procedure Sub (Var A : TLong; Const B : TLong; Const sp : Integer);
Var i, j : Integer;
{из А вычитаем В с учетом сдвига sp, результат вычитания в А}
Begin
For i := l To B[0] Do
Begin Dec(A[i+sp], B[i]);
j: = i;{*}
{реализация сложного заимствования}
while (A[j+sp] < 0) and (j <= A[0]) Do
Begin{*}
Inc(A[j+sp], Osn) ;
Dec(A[j+sp+l]); Inc(j); {*}
end; {*}
{Реализация простого заимствования.
Если операторы, отмеченные *, заменить
на нижеприведенные операторы в фигурных скобках, то,
по понятным причинам, логика не будет работать
при всех исходных данных. Можно сознательно сделать
ошибку и предложить найти ее — принцип "обучение через ошибку"}
{If A[i+sp]<0 Then Begin Inc(A[i+sp], Osn);
Dec (A[i+sp+l]);End;}
End;
i := A[0];
While (i > l) And (A[i] = 0) Do Dec(i);
A[0] := i
{корректировка длины результата операции}
End;
Рекомендуется выполнить трассировку работы данной процедуры, например, для следующих исходных данных. Число А равно 100000001000000000000, число В — 2000073859998.
Седьмая задача. Деление двух длинных чисел, т.е. нахождение целой части частного и остатка.
Написать исходную (без уточнений) часть логики не составляет труда. Это:
Procedure Long_Div_Long(Const А, В : TLong; Var Res, Ost : TLong);
Begin
FillChar(Res, SizeOf(Res), 0); Res[0] := 1;
FillChar(Ost, SizeOf(Ost), 0); 0st[0] := 1;
Case More(A, B, 0) Of
0: MakeDel(A, B, Res, Ost);
{А больше В, пока не знаем, как выполнять операцию - "выносим" в процедуру}
1: Ost:=A; {А меньше В}
2: Res[l] := l; {А равно В}
End;
End;
А дальше? Дальше начинаются проблемы. Делить столбиком нас научили в школе. Например,
1000143123567 |73859998
- 73859998 |----------
--------- |13541 (Целая часть частного)
261543143
- 221579994
----------
399631495
- 369299990
---------
303315056
- 295439992
----------
78750647
- 73859998
--------
4890649 (Остаток)
Что мы делали? На каждом этапе в уме подбирали цифру (1, 3, 5 и т.д.), такую, что произведение этой цифры на делитель дает число меньшее, но наиболее близкое к числу... Какому? Это трудно сказать словами, но из примера ясно. Зачем нам это делать в уме, пусть делает компьютер. Однако упростим пример, оставим его для тестирования окончательной логики процедуры, тем более что и числа "длинные". Пусть число А будет меньше В*10, тогда в результате (целой части деления) будет одна цифра. Например, А равно 564, а В — 63 и простая десятичная система счисления. Попробуем подобрать цифру результата, но не методом прямого перебора, а методом деления отрезка пополам. Пусть Down — верхняя граница интервала изменения подбираемой цифры, Up — нижняя граница интервала, Ost равен делимому.
| Down | Up | С = В * ( (Down + Up) Div 2) | Ost = 564 |
| 0 | 10 | 315 = 63 * ( (0 + 10) Div 2) | C < Ost |
| 5 | 10 | 441 = 63 * ( (5 + 10) Div 2) | C < Ost |
| 7 | 10 | 504 = 63 * ( (7 + 10) Div 2) | C < Ost |
| 8 | 10 | 567 = 63 * ( (8 + 10) Div 2) | C > Ost |
| 8 | 9 | 504 = 63 * ( (8 + 9) Div 2) | C < Ost |
Итак, результат — целая часть частного — равен (Up + Down) Div 2, остаток от деления — разность между значениями Ost и С. Нижнюю границу (Down) изменяем, если результат (С) меньше остатка, верхнюю (Up), — если больше.
Усложним пример. Пусть А равно 27856, а В — 354. Основанием системы счисления является не 10, а 10000.
| Down | Up | С | Ost = 27856 |
| 0 | 10000 | 1770000 | C > Ost |
| 0 | 5000 | 885000 | C > Ost |
| 0 | 2500 | 442500 | C > Ost |
| 0 | 1250 | 221250 | C > Ost |
| 0 | 625 | 110448 | C > Ost |
| 0 | 312 | 55224 | C > Ost |
| 0 | 156 | 27612 | C < Ost |
| 78 | 156 | 41418 | C > Ost |
| 78 | 117 | 34338 | C > Ost |
| 78 | 97 | 30798 | C > Ost |
| 78 | 87 | 29028 | C > Ost |
| 78 | 82 | 28320 | C > Ost |
| 78 | 80 | 27966 | C > Ost |
| 78 | 79 | 27612 | C < Ost |
Целая часть частного равна 78, остаток от деления — 27856 минус 27612, т.е. 244.
Пора приводить процедуру. Используемые "кирпичики": функция сравнения чисел (More) с учетом сдвига и функция умножения длинного числа на короткое (Mul) описаны выше.
Function FindBin(Var Ost : Tlong; Const В : TLong; Const sp : Integer) : Longint;
Var Down, Up : Word; C : TLong;
Begin
Down := 0;Up := 0sn;
{основание системы счисления}
While Up - l > Down Do
Begin
{Есть возможность преподавателю сделать
сознательную ошибку. Изменить условие
цикла на Up>Down. Результат - зацикливание программы.}
Mul(В, (Up + Down) Div 2, С);
Case More(Ost, C, sp) Of
0: Down := (Down + Up) Div 2;
1: Up := (Up + Down) Div 2;
2: Begin Up := (Up + Down) Div 2; Down := Up End;
End;
End;
Mul(B, (Up + Down) Div 2, C);
If More (Ost, C, 0) = 0 Then Sub(Ost, C, sp)
{находим остаток от деления}
Else begin Sub (C, Ost, sp); Ost := C end;
FindBin := (Up + Down) Div 2;
{целая часть частного}
End;
Осталось разобраться со сдвигом, значением переменной sp в нашем изложении. Опять вернемся к обычной системе счисления и попытаемся разделить, например, 635 на 15. Что мы делаем? Вначале делим 63 на 15 и формируем, подбираем в уме первую цифру результата. Подбирать с помощью компьютера мы научились. Подобрали — это цифра 4, и это старшая цифра результата. Изменим остаток. Если вначале он был 635, то сейчас стал 35. Вычитать с учетом сдвига мы умеем. Опять подбираем цифру. Вторую цифру результата. Это цифра 2 и остаток 5. Итак, результат (целая часть) 42, остаток от деления 5. А что изменится, если основанием будет не 10, а 10000? Логика совпадает, только в уме считать несколько труднее, но ведь у нас же есть молоток под названием компьютер — пусть он вбивает гвозди.
Procedure MakeDel(Const А, В : TLong; Var Res, Ost : TLong);
Var sp : Integer;
Begin
Ost := A; {первоначальное значение остатка}
sp := А[0] - В[0];
If More(А, В, sp) = l Then Dec(sp);
{B * Osn > A, в результате одна цифра}
Res[0] := sp + l;
While sp >= 0 Do
Begin
{находим очередную цифру результата}
Res[sp + 1] := FindBin(Ost, B, sp);
Dec(sp)
End
End;
Методические рекомендации. Представленный материал излагается на четырех занятиях по известной схеме: 10-15-минутное изложение идей, а затем работа учащихся под руководством преподавателя.
1-е занятие. Ввод, вывод и сложение длинных чисел (задачи 1, 2, 3).
2-е занятие. Функции сравнения (задача 4).
3-е занятие. Умножение и вычитание длинных чисел (задачи 5, 6).
4-е занятие. Деление длинных чисел (задача 7). Безусловно, эта схема не догма. В зависимости от уровня подготовки учащихся на самостоятельное выполнение может быть вынесена значительная часть материала. Замечу только, что в силу сложившейся традиции в ряде случаев допускаются при изложении сознательные ошибки. В результате работы каждый учащийся должен иметь собственный модуль для работы с "длинными" числами.
Темы для исследований
1. Решение задач: поиск наибольшего общего делителя двух "длинных" чисел; поиск наименьшего общего кратного двух "длинных" чисел; извлечение квадратного корня из "длинного" числа и т.д.
2. "Длинные" числа могут быть отрицательными. Как изменятся описанные выше операции для этого случая?
3. Для хранения "длинных" чисел используется не массив, а стек, реализованный с помощью списка. Модифицировать модуль работы с "длинными" числами.
Список литературы
С.М. Окулов/ "Длинная" арифметика/
Для подготовки данной работы были использованы материалы с сайта http://www.comp-science.narod.ru/
Похожие работы
... ее работы. Вернемся к вычислению факториала. Используя разработанные подпрограммы, определим, значение факториала какого максимального числа можно разместить в памяти при таком представлении длинных чисел. Вот измененный фрагмент основной программы, решающий поставленную задачу. Begin MaxF := 810; Zero(F); F[1] := 1; For I := 1 To MaxF Do Begin Str(I, S); {преобразование числа I к ...
... кратчайшего пути между u и v, что невозможно. Это свойство кратчайших путей позволяет решать задачу их нахождения методом динамического программирования. Покажем сначала как можно записать “волновой алгоритм” так, что задача поиска кратчайшего пути между двумя вершинами графа будет решаться за O(N2) действий. Задача 12. Для линий метрополитена некоторого города известно, между какими парами линий ...
... .h" #define CR "n" void main() { ofstream r("report.txt",1); ostream_withassign rc; rc=cout; cout<<"nТестовая программа для класса UNLIMn" <<"(целые числа с произвольной точностью)n" ; cout=r; r<<"Отчет тестовой программыn" <<"nПроверка работы конструкторов:n" <<" Без инициализации:n" ; r<<" unlim a;n"; unlim a; r<<" a="<<a<<"n" ...
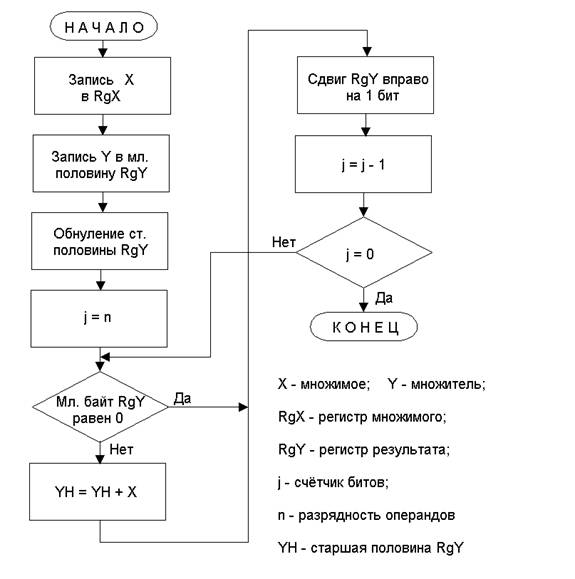
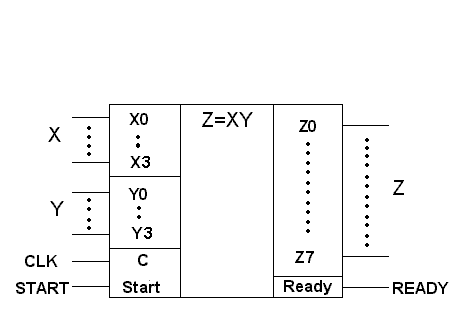
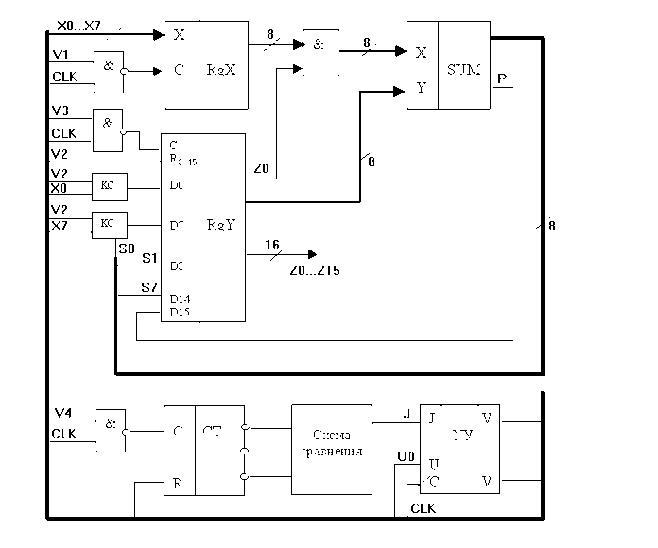
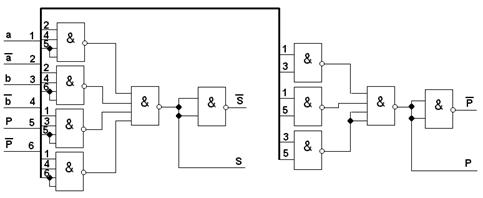
... RgХ и RgY имеют как прямые, так и инверсные выходы , что позволяет уменьшить количество элементов в сумматоре. Рисунок 2.2 Структурная схема АЛУ для умножения двоичных чисел. Как видно из схемы активный уровень сигналов управления - высокий, и устройство управления тактируется по фронту импульса, а исполнительные устройства - по спаду, что позволяет избежать гонок в схеме. 3 Синтез ...
0 комментариев