СОДЕРЖАНИЕ
ЗАДАЧА1
ЗАДАЧА 2
ЗАДАЧА 3
ЗАДАЧА 4
Задача 1
Имеются следующие отчетные данные 25 заводов одной из отраслей промышленности:
темп роста индекс статистический
| Номер завода | Среднегодовая стоимость основных производственных фондов, млрд.руб. | Объем продукции в сопоставимых ценах, млрд.руб. |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | 3,4 3,1 3,5 4,1 5,8 5,2 3,8 4,1 5,6 4,5 4,2 6,1 6,5 2,0 6,4 4,0 8,0 5,1 4,9 4,3 5,8 7,2 6,6 3,0 6,7 | 3,5 3,3 3,5 4,5 7,5 6,9 4,3 5,9 4,8 5,8 4,6 8,4 7,3 2,1 7,8 4,2 10,6 5,8 5,3 4,9 6,0 10,4 6,9 3,5 7,2 |
С целью изучения зависимости между среднегодовой стоимостью основных производственных фондов и выпуском валовой продукции произведите группировку заводов по среднегодовой стоимости основных производственных фондов, образовав четыре группы заводов с равными интервалами. По каждой группе и совокупности заводов подсчитайте:
1) число заводов;
2) среднегодовую стоимость основных производственных фондов всего и в среднем на один завод;
стоимость валовой продукции — всего и в среднем на один завод; размер валовой продукции на один рубль основных производственных фондов (фондоотдачу).
Результаты представьте в виде групповой таблицы. Напишите краткие выводы.
| Группы заводов по среднегод. стоимости ОПФ | Число заводов | Среднегодовая стоимость ОПФ, млрд. руб. | Выпуск вал. продукции, млрд. руб. |
| 2,0 – 3, 5 |
| 3,4 3,1 3,5 2,0 3,0 | 3,5 3,3 3,5 2,1 3,5 |
| Итого | 5 | 15 | 15,9 |
| 3,5 – 5,0 | 4,1 4,1 4,5 4,2 4,0 4,9 4,3 3,8 | 5,9 5,9 5,8 4,6 4,2 5,3 4,9 4,3 | |
| Итого | 8 | 33,9 | 40,9 |
| 5,0 – 6,5 | 5,8 5,1 6,4 6,5 6,1 5,6 5,2 5,8 | 6,0 5,8 7,8 7,3 8,4 4,8 6,9 7,5 | |
| Итого | 8 | 46,5 | 54,5 |
| 6,5 – 8,0 | 8,0 7,2 6,7 6,6 | 10,6 10,4 7,2 6,9 | |
| Итого | 4 | 28,5 | 35,1 |
Макет групповой таблицы
| Группы заводов по среднегодовой стоимости ОПФ, млрд. руб. | Количество заводов | Среднегодовая стоимость ОПФ, млрд. руб. | Стоимость валовой продукции, млрд. руб. | Фондоотдача, млрд. руб. | ||
| всего | на 1 завод | всего | на 1 завод | |||
| 2,0 – 3,5 3,5 – 5,0 5,0 – 6,5 6,5 – 8,0 | 5 8 8 4 | 15 33,9 46,5 28,5 | 3 4,2 5,8 7,1 | 15,9 40,9 54,5 35,1 | 3,1 5,1 6,8 8,7 | 1,03 1,21 1,17 1,22 |
| Итого | 25 | 123,9 | 20,1 | 146,4 | 23,7 | 4,63 |
Вывод:
Была произведена группировка заводов по среднегодовой стоимости основных производственных фондов.
Было подсчитано, что в интервале:
2,0 – 3,5: 5 заводов;
3,5 – 5,0: 8 заводов;
5,0 – 6,5: 8 заводов;
6,5 – 8,0: 4 завода.
Среднегодовая стоимость основных производственных фондов в интервале:
2,0 – 3,5 всего составила 15 млрд. руб., а в среднем на 1 завод – 3 млрд. руб.;
3,5 – 5,0 всего составила 33,9 млрд. руб., а в среднем на 1 завод – 4,2 млрд. руб.
5,0 – 6,5 всего составила 46,5 млрд. руб., а в среднем на 1 завод – 5,8 млрд. руб.
6,5 – 8,0 всего составила 28,5 млрд. руб., а в среднем на 1 завод – 7,1 млрд. руб.
Общая среднегодовая стоимость основных производственных фондов заводов составила 123,9 млрд. руб., на 1 завод – 20,1 млрд. руб.
Стоимость валовой продукции в интервале:
2,0 – 3,5 всего 15,9 млрд. руб., а в среднем на 1 завод – 3,1 млрд. руб.;
3,5 – 5,0 всего 40,9 млрд. руб., а в среднем на 1 завод – 5,1 млрд. руб.;
5,0 – 6,5 всего 54,5 млрд. руб., а в среднем на 1 завод – 6,8 млрд. руб.;
6,5 – 8,0 всего 35,1 млрд. руб., а в среднем на 1 завод – 8,7 млрд. руб.;
Общая стоимость валовой продукции по заводам составила 146,4 млрд. руб., на 1 завод – 23,7 млрд. руб.
Размер фондоотдачи в интервале:
2,0 – 3,5 составляет 1,03 млрд. руб.;
3,5 – 5,0 составляет 1,21 млрд. руб.;
5,0 – 6,5 составляет 1,17 млрд. руб.;
6,5 – 8,0 составляет 1,22 млрд. руб.;
Всего фондоотдача составила 4,63 млрд. руб.
Задача 2
Имеются следующие данные по зерновым культурам колхоза:
| В отчетном периоде | План на предстоящий период | |||
| культура | Урожайность | Валовый | Урожайность | Посевная |
| Ц | Сбор | Ц | Площадь | |
| с 1 Га | Ц | с 1 Га | Га | |
| Пшеница | 21,0 | 63000 | 23,0 | 3300 |
| Ячмень | 19,0 | 38000 | 20,0 | 1300 |
Вычислите среднюю урожайность зерновых культур по колхозу: 1) в отчетном периоде; 2) в планируемом периоде.
Укажите, какой вид средней надо применять для вычисления этих показателей и какие изменения урожайности предусмотрены в плане на предстоящий период.
Для того, чтобы вычислить среднюю урожайность зерновых культур по колхозу необходимо вычислить данные: валовый сбор на планируемый период;
посевная площадь в отчетном периоде;
Валовый сбор на планируемый период:
1) пшеница: 23*3300 = 75 900 Ц
2) ячмень: 20*1300 = 26 000 Ц
Посевная площадь в отчетном периоде:
1)пшеница: 63 000:21 = 3000 Га
2)ячмень: 38 000: 19 = 2000 Га
Отразим найденные данные в таблице:
| Культура | В отчетном периоде | План на предстоящий период | ||||
| Урожайность Ц с 1Га | Валовый сбор Ц | Посевная площадь Га | Урожайность Ц с 1Га | Валовый сбор Ц | Посевная площадь Га | |
| Пшеница | 21,0 | 63 000 | 3000 | 23,0 | 75 900 | 3300 |
| Ячмень | 19,0 | 38 000 | 2000 | 20,0 | 26 000 | 1300 |
Средняя урожайность культур в отчетном и плановом периодах была найдена при помощи средней гармонической.
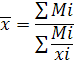
Средняя урожайность в отчетном периоде:
![]()
![]()
![]() ;
;
![]() =
= ![]() = 20,2 Ц с 1 Га
= 20,2 Ц с 1 Га
Средняя урожайность культур в плановом периоде:
![]()
![]()
![]() ;
;
![]() =
=![]() 22,1 Ц с 1 Га
22,1 Ц с 1 Га
Вывод:
средняя урожайность пшеницы в отчетном периоде составляет 21,0 Ц с 1 Га;
средняя урожайность ячменя в отчетном периоде составляет 19,0 Ц с 1 Га.
Средняя урожайность пшеницы в планируемом периоде на 2 Ц с 1 Га, а ячменя на 1 Ц с 1 Га.
Задача 3
Производство чугуна в СССР характеризуется следующими данными:
| Годы | Производство чугуна, млн.т |
| 1980 1981 1982 1983 1984 1985 | 107 108 107 110 111 110 |
Для анализа динамики производства чугуна вычислите:
1)абсолютные приросты (или снижение), темпы роста и темпы прироста (или снижения) по годам и к 1980 г., абсолютное содержание одного процента прироста (снижения). Полученные данные представьте в таблице;
2)среднегодовое производство чугуна;
3)среднегодовой темп роста и прироста производства чугуна.
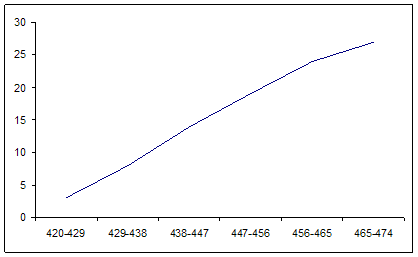
4)Постройте график динамики производства чугуна в СССР за 1980 — 1985 гг.
5)Сделайте выводы.
Решение:
1)
Методы нахождения темпов роста:
а) базисный: Тб = Yi/Yo * 100
б) цепной: Тц =Yi/Yi-1 * 100
Методы нахождения темпов прироста:
а) базисный: ∆Тб = ∆Yб/Yб * 100
б) цепной: ∆ Тц = ∆ Yц/Yi-1 *100
Абсолютный прирост:
а) базисный: ∆Yб = Yi – Yo
б) цепной: ∆Yц = Yi – Yi-1
Абсолютное значение 1% прироста:
А% = Yi-1 : 100
2) Среднегодовое производство чугуна: ![]() (средняя арифметическая простая)
(средняя арифметическая простая)
![]()
Среднегодовое производство чугуна с 1980 по 1985 составило 108.83 млн.т
3) Среднегодовой темп роста производства чугуна:
В среднем за весь период с 1980 по 1985 рост производство чугуна составило 1.0055
Среднегодовой темп прироста производства чугуна:
![]()
В среднем каждый период производства чугуна увеличивался на 0.0055%
Сведем полученные данные в таблицу.
Динамика показателей абсолютного прироста (снижения), темпа роста (снижения), темпа прироста (понижения), абсолютного значения 1 % прироста производства чугуна исчисленные базисным и цепным способами:
Динамика производства чугуна в СССР за 1980 — 1985 гг.
| Показатели | Единицы измерения | Годы | |||||
| 1980 | 1981 | 1982 | 1983 | 1984 | 1985 | ||
| Производство чугуна Темп роста - базисный -цепной | млн. т % | 107 100 - | 108 100,9 100,9 | 107 100 99 | 110 102,8 102,8 | 111 103,7 100,9 | 110 102,8 99 |
| Абсолютный прирост - базисный - цепной | тыс. руб. | - - | 1 1 | 0 -1 | 3 3 | 4 1 | 3 -1 |
| Темп прироста - базисный -цепной | % | - - | 0,9 0,9 | 0 -0,93 | 2,8 2,8 | 3,7 0,9 | 2,8 -0,9 |
| Абсолютное значение 1% прироста | тыс. руб. | - | 1,07 | 1,08 | 1,07 | 1,1 | 1,11 |
Вывод: производство чугуна в 1985 г. составило 110 млн.т. В 1985 по сравнению с 1980 производство чугуна увеличилось на 3 млн.т или на 2.8% .
Темпы роста и прироста между 1980 г. и 1981 г. составляют 1 млн. т или 100,9%; между 1980 г. и 1982 г. показатели равны, но при этом соотношение 1981 г. и 1982г. показывает, что темп роста был снижен на 1 млн. т или -0,93 %; между 1980 г. и 1983 г. наблюдается темп роста на 3 млн. т или 2,8%; если же рассматривать 1982 г. или 1983 г., то также наблюдается увеличение на 3 млн. т или 2,8 %; между 1980 г. и 1984 г. также заметен рост на 4 млн.т или 3,7 %, в сопоставлении 1984 г. и 1983 г. виден рост на 1 млн.т или 0,9 %.
Абсолютный прирост в базисном методе в 1981 г. равен 1 млн. т, в 1982 г. он остается равным 1980 г., в 1983 г. увеличивается на 3 млн. т, в 1984 г. на 4 млн. т и 1985 г. равен 3 млн. т. Но если мы рассмотрим абсолютный прирост в цепном методе что 1981 г. по отношению к 1980 г. увеличился на 1 млн. т, 1982 г. по отношению к 1981 г. снизился на 1 млн. т, 1983 г. по отношению к 1982 г. увеличен на 3 млн. т , 1984 г. по отношению к 1983 г. увеличен на 1 млн. т, 1985 г. по отношению к 1984 г. снизился на 1 млн. т.
Максимальный прирост наблюдается в 1983 (3 млн.т). Минимальный прирост зафиксирован в 1982 (-1 млн.т).
Абсолютное значение 1 % прироста в 1981 г. составляет 1,07 тыс. руб., в 1982 г. – 1,08 тыс. руб., в 1983 г. – 1,07 тыс. руб., в 1984 г. – 1,1 тыс. руб., в 1985 г. – 1,11 тыс.руб.
В среднем, сопоставив все данные мы заметим, что в производстве чугуна наблюдается положительная динамика, т.е. увеличение показателей роста, прироста, что имеет позитивный характер для данного вида производства.
Задача 4
Динамика себестоимости и объема производства продукции характеризуется следующими данными:
| Вид | Выработано продукции, тыс.ед | Себестоимость единицы продукции т.руб | ||
| продукции | базисный | отчетный | базисный | отчетный |
| период | период | период | период | |
| Завод №1 | ||||
| МП-25 | 4,5 | 5,0 | 5,0 | 4,8 |
| ММ-29 | 3,2 | 3,0 | 8,0 | 8,2 |
| Завод №2 | ||||
| МП-25 | 10,6 | 10,0 | 7,0 | 6,6 |
На основании имеющихся данных вычислите:
1. Для завода № 1 (по двум видам продукции вместе):
а) общий индекс затрат на производство продукции;
б) общий индекс себестоимости продукции;
в) общий индекс физического объема производства продукции.
Определите в отчетном периоде изменение суммы затрат на производство продукции и разложите по факторам (за счет изменения себестоимости и объема выработанной продукции).
Покажите взаимосвязь между исчисленными индексами.
2. Для двух заводов вместе (по продукции МП-25):
а) индекс себестоимости переменного состава;
б) индекс себестоимости постоянного состава;
в) индекс влияния изменения структуры производства продукции на динамику средней себестоимости.
Объясните разницу между величинами индексов постоянного и переменного состава.
Решение:
1 а) общий индекс затрат на производство продукции 1 завода
I = ![]() =
= ![]() = 1,01
= 1,01
∆Z = ∑q1 ∙ z1 - ∑q0 ∙ z0
∆Z =48,6 – 48,1 = 0,5
За счет всех факторов общие затраты увеличились на 0,5
б) общий индекс себестоимости продукции
Iz= ![]() =
= ![]() = 0,99
= 0,99
∆Zz = ∑q1 ∙ z1 - ∑q1 ∙ z0
∆Zz = 48,6 - 49 = - 0,4
За счет изменения себестоимости общие затраты снизились на 0.4
в) общий индекс физического объема продукции (индекс Ласпейреса)
Iq= ![]() =
= ![]() = 1,02
= 1,02
∆Zq = ∑q1 ∙ z0 - ∑q0 ∙ z0
∆Zq = 49 – 48,1 = 0,9
За счет изменения объема выработанной продукции, общие затраты увеличились на 3.3
Покажем взаимосвязь индексов
I = Iq ∙ Iz= 0.99 ∙ 1,02 = 1,0098
2)
а) индекс себестоимости переменного состава
Средняя себестоимость за отчетный период
Средняя себестоимость за базисный период
За счет всех факторов себестоимость снизилась на 6.31%
б) индекс себестоимости постоянного состава
За счет изменения структуры себестоимости средняя себестоимость снизилась на 5.26%
в) индекс влияния изменения структуры производства продукции на динамику средней себестоимости
За счет изменения структуры выработанной продукции средняя себестоимость снизилась на 1.1%
Похожие работы
... , табличные характеристики связи. Это в свою очередь потребовало решения соответственно теоретико-методологических проблем. Глава 2. Абсолютные и относительные величины 2.1. Понятие, формы выражения и виды статистических показателей Статистическое исследование независимо от его масштабов и целей всегда завершается расчетом и анализом различных по виду и форме выражения статистических ...
... по их запросам статистическая информация предоставляется на платной основе. Статистической информации с ограниченным доступом предоставляется пользователям в соответствии с законодательством Российской Федерации. 2. Формирование единого информационного пространства В процессе осуществления статистического учета Федеральные органы исполнительной власти и их территориальные органы ...
... : х - стаж по специальности; f - накопленная частота. Графики являются важным средством выражения и анализа статистических данных, поскольку наглядное представление облегчает восприятие информации. Графики позволяют мгновенно охватить и осмыслить совокупность показателей - выявить наиболее типичные соотношения и связи этих показателей, определить тенденции развития охарактеризовать структуру и ...
... наблюдения – можно ли распространить результаты выборочной совокупности на генеральную совокупность или нет, следовательно, проверка выборочной совокупности на точность это необходимая часть анализа при несплошном наблюдении. Существуют два вида оценок статистических показателей на точность: точечная и интервальная. Точечная представляет собой оценку параметра в генеральной совокупности одним чи
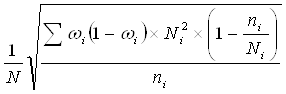
0 комментариев