Статистические показатели, их определение

Задача 1

При выборочном бесповторном собственно-случайном отборе 5% коробок конфет со стандартным весом 20 кг получены следующие данные о недовесе.

Недовес 1 коробки, кг	0,4-0,6	0,6-0,8	0,8-1,0	1,0-1,2	1,2-1,4
Число обследованных коробок	10	18	36	26	10

Определите:

1) средний недовес одной коробки конфет и его возможные пределы

(с вероятностью Р=0,954);

2) долю коробок с недовесом до 1 кг;

3) возможные пределы доли коробок с недовесом до 1 кг

(с вероятностью 0,683). Сделайте выводы.

Решение:

1) средний недовес одной коробки конфет и его возможные пределы

(с вероятностью Р=0,954);

Недовес 1 коробки, кг	Число обследованных коробок f	Середина интервала х	хf		2	2f
0,4-0,6	10	0,5	5	-0,416	0,17306	1,73056
0,6-0,8	18	0,7	12,6	-0,216	0,04666	0,83981
0,8-1,0	36	0,9	32,4	-0,016	0,00026	0,00922
1,0-1,2	26	1,1	28,6	0,184	0,03386	0,88026
1,2-1,4	10	1,3	13	0,384	0,14746	1,47456
Итого:	100	-	91,6	-	-	4,9344

=91,6/100=0,9 – средний недовес одной коробки

=4,9344/100=0,493

=2*=0,193

Вычислим пределы среднего недовеса одной коробки для всей партии:

0,9-0,230,9+0,23

0,71,13

С вероятностью 0,954 (т.е. в 95,4 коробках из 100) можно утверждать, что средний недовес колеблется в пределах от 0,7 до 1,13 кг.

2) долю коробок с недовесом до 1 кг;

3) возможные пределы доли коробок с недовесом до 1 кг

(с вероятностью 0,683). Сделайте выводы.

0,27

0,64-0,270,64+0,27

0,370,91

С вероятностью 0,683 (то есть в 68,3 коробках из 100) можно гарантировать, что доля недовеса до 1 кг будет находиться в пределах от 0,37 до 0,91 кг.

Задача 2

Ежегодные темпы прироста реализации товара «А» составили в % к предыдущему году:

1998 – 5,5;

1999 – 6,2;

2000 – 8,4;

2001 – 10,5;

2002 – 9,2

Исчислите за приведённые годы базисные темпы роста по отношению к 1997 г. и среднегодовой темп прироста за 1998 – 2002 гг.

Решение

Приведём исходные данные в таблице

Год	Темп прироста цепной, %
1997	-
1998	5,5
1999	6,2
2000	8,4
2001	10,5
2002	9,2

Воспользуемся связью цепных и базисных темпов роста

Составим расчётную таблицу

Год	Темп прироста цепной, %	Темп роста цепной	Темп роста базисный	Темп прироста базисный, %
1997	-	-	1,000	-
1998	5,5	1,055	1,055	5,5
1999	6,2	1,062	1,120	12,0
2000	8,4	1,084	1,215	21,5
2001	10,5	1,105	1,342	34,2
2002	9,2	1,092	1,466	46,6

При этом среднегодовой темп роста за 1998 – 2002 гг. равен

,

или 108,0%

Тогда среднегодовой темп роста за 1998 – 2002 гг. равен 108,0% - 100%=8,0%

 

Задача 3

Имеются следующие выборочные данные о расходах на платные услуги домохозяйств района:

Домохозяйство	Обследовано домохозяйств	Доля расходов на платные услуги, %
Городское	400	30
Сельское	100	10

Определите для домохозяйств района:

1.  общую дисперсию;

2.  среднюю из групповых дисперсий;

3.  межгрупповую дисперсию, используя правило сложения дисперсий;

4.  эмпирический коэффициент детерминации;

5.  эмпирическое корреляционное отношение. Поясните полученные показатели.

Решение:

- общую дисперсию по правилу сложения дисперсии;

Обследовано домохозяйств f	Доля расходов на платные услуги х	()	()2	()2f
400	30	4	16	6400
100	10	-16	256	25600
500				32000

==32000/500=26

=32000/500=64

Домохозяйство f	Доля расходов на платные услуги х	()	()2	()2f
400	30	10	100	40000
100	10	-10	100	10000
500	40			50000

=40/2=20

=50000/500=100

=100+64=164

- эмпирическое корреляционное отношение.

==0,80

Чем значение корреляционного отношения ближе к единице, тем теснее, ближе к функциональной зависимости связь между признаками.

- эмпирический коэффициент детерминации

=0,64

Это означает, что на 64% вариация расходов обусловлена тем, что услуги являются платными и 36% бесплатными.

 

Задача 4

По отделению банка имеются следующие данные о вкладах населения:

Виды вкладов	Базисный период				Отчетный период
	Количество счетов		Остаток вкладов, тыс. руб.		Количество счетов		Остаток вкладов, тыс. руб.
Депозитный	10000	10200		10500		11200
Срочный	2500		5400		4200		5800
Выигрышный	500		250		400		280
Итого:	13000		15850		15100		17280

Определите

1) Средний размер вклада в базисном и отчетном периодах.

2) Индексы среднего размера вклада:

·  переменного состава;

·  постоянного состава;

·  структурных сдвигов.

Покажите взаимосвязь рассчитанных индексов.

Решение:

1)

(баз)= 15850/13000=1,219 тыс.руб.

(отч)= 17280/15100=1,144 тыс.руб.

2) Индекс переменного состава:

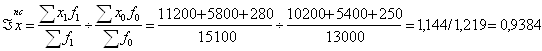
Следовательно, средний размер вклада по данным трем видам в отчетном году снизился на 6,16%

Индекс постоянного состава:

Следовательно, средний размер вклада по данным видам снизился на 13,5% в результате изменения только одного фактора – самого вклада по каждому виду.

Индекс структурных сдвигов:

Следовательно, увеличение доли видов вклада с меньшим его размером в общей сумме привело к увеличению среднего вклада по трем видам вместе на 8,55%.

3) Покажите взаимосвязь рассчитанных индексов:

 1,0855*0,8645=0,9384

  Задача 5

Валовой выпуск товаров и услуг в рыночных ценах в производственной сфере Российской Федерации за отчётный период составил 5130,2 млрд. руб., в непроизводственной сфере – 1520,9 млрд. руб. Условно исчисленная продукция финансового посредничества в экономике составила 126,8 млрд. руб. Определите валовую добавленную стоимость по сферам деятельности и в целом по экономике, если промежуточное потребление в производственной сфере составило 2790,5 млрд. руб., в непроизводственной – 680,3 млрд. руб.

Решение

Валовая добавленная стоимость (ВДС) определяется как разность между стоимостью выпуска товаров и услуг (ВВ) и промежуточным потреблением (ПП)

В производственной сфере

 млрд. руб.

дисперсия корреляционный валовый стоимость прирост

В непроизводственной сфере

 млрд. руб.

В целом по экономике

 млрд. руб.

 млрд. руб.

Тогда

 млрд. руб.

Задача 6

Имеются следующие данные по области на начало текущего года (тыс. чел.)

Население рабочего возраста1	880
Нетрудоспособное население рабочего возраста1	58,5
Фактически работающие пенсионеры и подростки12	31,8
Из общей численности трудоспособного населения занято работой и учёбой в других областях2	12,8
Занято частным предпринимательством2	181,8
Занято на производственных предприятиях2	564,1
Учащиеся с отрывом от производства рабочего возраста2	35,9
Занято в домашнем хозяйстве и уходом за детьми2	68,4
Из общей численности занятых и учащихся проживает в других областях2	9,3

Определите

1) численность трудовых ресурсов двумя методами;

2) коэффициенты занятости трудовых ресурсов (с учётом и без учёта учащихся)

Решение

Трудовые ресурсы – это население обоего пола, способное к труду по возрасту и состоянию здоровья. Численность трудовых ресурсов определяется двумя методами:

-по источникам формирования (демографический метод) – исходя из численности населения в трудоспособном возрасте за исключением инвалидов I и II групп и лиц, получающих пенсию по возрасту на льготных условиях. В трудовые ресурсы включаются работающие лица нетрудоспособного возраста. В настоящее время границами трудоспособного возраста в России считают 16-54 года – для женщин и 16 – 59 лет – для мужчин

-по фактической занятости (экономический метод) – как совокупность всего фактически занятого населения, включая работающих пенсионеров и подростков, а также лиц трудоспособного возраста, занятых в домашнем хозяйстве и уходом за детьми, учащихся с отрывом от производства старше 16 лет, безработных

1) Демографический метод

880-58,5=821,5

– трудоспособное население рабочего возраста

821,5+31,8=853,3

– трудовые ресурсы

ТР=880-58,5+31,8=853,3 тыс. чел.

Экономический метод

Занятые

181,8+564,1+68,4+31,8+35,9=882

В других областях

9,3+12,8=22,1

ТР=882-22,1=859,9 тыс. чел.

Численное расхождение возможно из – за не точных данных

2) Всего учащихся 35,9

Коэффициент занятости с учётом учащихся равен

К_з=859,9/882=0,975

Коэффициент занятости без учёта учащихся равен

К_з=(859,9-35,9)/882=0,934

Задача 7

Имеются следующие данные о движении основных производственных фондов, тыс. руб.:

1. Первоначальная стоимость ОПФ за вычетом износа на начало года	3875
2. Сумма износа на начало года	2075
3. Введено в действие новых ОПФ за год	1090
4. Выбыло в течение года ОПФ: по полной стоимости по остаточной стоимости	670 300
5. Начислено амортизации на полное восстановление ОПФ за год	60,3
6. Объем продукции (работ, услуг)	3800
7. удельный вес активной части ОПФ	55%

Определите:

1) Коэффициент годности ОПФ на начало года;

2) коэффициенты ввода и выбытия;

3) Фондоотдачу всех ОПФ и активной части;

4)Фондоемкость продукции

Решение:

1)Кгодности=

=

2) полную стоимость ОПФ на начало и конец года;

Фн=3875+2075=5950 тыс. руб.

Фк=Фн+Фп-Фв=5950+1090-670=6370 тыс. руб.

3) коэффициенты вода и выбытия ОПФ на начало года

Кввода=

Квыбытия=

Кизноса==

Кгодности==

4) Фондоотдача = Объем продукции / Стоимость

ОС = 3800/6679,7 = 0,99 (р. с 1р. средств)

Фондоотдача (акт.части)= Объем продукции / Стоимость

ОС = 3800/3673,8 = 1,03(р. с 1р. средств)

Фондоемкость = Стоимость ОС / Объем продукции = 6679,7/3800 = 1,01

Баланс по полной восстановительной стоимости за вычетом износа

Наличие на начало года	Введено	Выбыло всего			Наличие на конец года
		Ликвидировано	Выбыло	Износ за год
1	2	3	4	5	6
5950	1090		670	60,3	6679,7

Литература

1.  Гусаров В.М. Теория статистики: Учебное пособие. – М.: Юнити, 2003.

2.  Елисеева И.И., Юзбашев М.М. Общая теория статистики: Учебник. – 4-ое изд. перераб. и доп. – М.: Финансы и статистика, 2002.

3.  Статистика: Учебное пособие под ред. Ионина В.Г. – 2-ое изд. перераб. и доп. – М.: ИНФРА-М, 2005.

4.  Теория статистики: Учебник под ред. Р.А. Шмойловой – 4-ое изд., перераб. и доп. – М.: Финансы и статистика, 2005.