Лабораторная работа №3
Имитационное моделирование работы систем массового обслуживания
Цель работы: научиться определять функциональные характеристики системы массового обслуживания на основе имитационного моделирования; приобрести опыт синтеза систем массового обслуживания с заданными характеристиками.
Задание
1. Разработать программу на языке SIMNET II, для моделирования описанной ситуации согласно своему варианту.
2. Загрузить среду SIMNET II (файл SIMEDIT.BAT). В редакторе системы набрать текст разработанной программы или прочитать созданную в другом текстовом редакторе имитационную модель (клавиша F2).
3. Выполнить имитацию процесса работы СМО. Подбирая требуемый параметр, получить СМО с требуемыми характеристиками.
4. Рассчитайте основные функциональные характеристики работы оптимальной СМО на основе полученных результатов имитационного моделирования. Запишите полученные результаты в таблицу 3.1. Завершите сеанс работы с системой (сочетание клавиш Alt-X).
5. Оформите отчет о проделанной работе.
Вариант 1
Определить оптимальное число телефонных номеров, необходимых для установки на коммерческом предприятии при 8 часовом рабочем дне при условии, что заявки на переговоры поступают с интенсивностью 90 заявок/час, а средняя продолжительность разговора по телефону составляет 2 мин. Статистические наблюдения показали, что сделкой заканчивается только 10% разговоров. Средний доход от одной сделки составляет 25 ден. ед., а стоимость использования одной телефонной линии — 0,9 ден. ед./час.
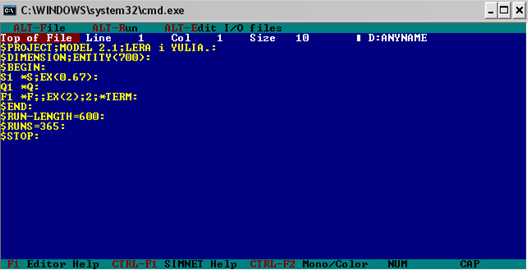
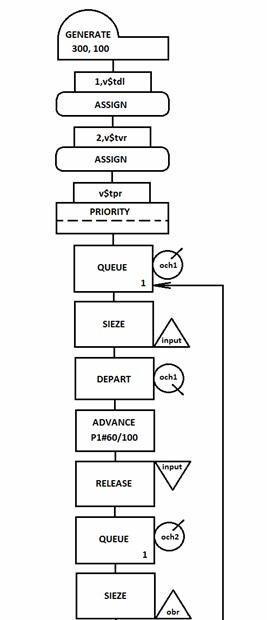
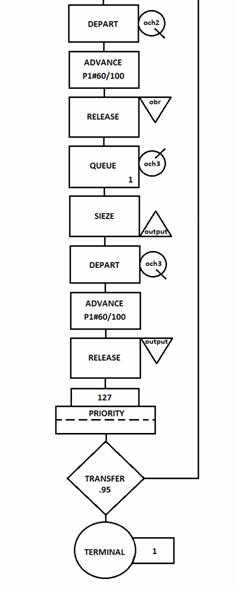
Программа, моделирующая работу системы массового обслуживания, имеет вид.
$PROJECT;Model 2.1;Lera I Yulia:
$DIMENSION;ENTITY(700):
$BEGIN:
S1 *S;EX(0.67):
Q1 *Q:
F1 *F;;EX(2);3;*TERM:
$END:
$RUN-LENGTH=600:
$RUNS=365:
$STOP:
По условию задачи требуется найти такое количество каналов обслуживания, при котором прибыль предприятия будет максимальной. В модели будем подбирать второй параметр строки F1 (выделен курсивом).
При с=5:П = 816*0,1*25 – 5*0,9 = 2235,5 ден.ед.
При с=4:П = 835*0,1*25 – 4*0,9 = 2251,4 ден.ед.
При с=2:П = 860*0,1*25 – 2*0,9 = 2379,8 ден.ед.
При с=1:П = 824*0,1*25 – 1*,09 = 2148,2 ден.ед.
Таким образом, максимальная прибыль достигается при установлении трех телефонных линий. Программа имитационного моделирования для оптимального режима работы примет вид:
имитационный моделирование массовый обслуживание
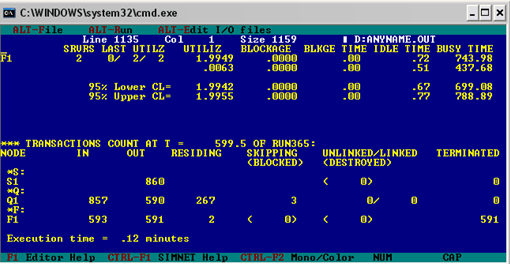
Результаты расчетов функциональных характеристик СМО:
| Характеристика | Значение |
| l | 1/0,67 = 1,5 зв./мин. |
| m | 60/2=30 зв./мин. |
| с | 3 |
| время моделирования | 599,5 мин. |
| общее количество заявок | 860 зв. |
| количество отказов в обслуживании | 0 зв. |
| количество обслуженных заявок | 860-0=860 = 2240 |
| pотк | 0/860=0% |
| q | 1 – 0 = 1% |
| эфф | 860/599,5 = 1,43 зв./мин. |
| Lq | 2,14 зв. |
| Wq | 0,58 мин. |
Контрольные вопросы
1. Какие задачи принятия решений могут быть сформулированы применительно к системам массового обслуживания?
Среди основных моделей принятия решений можно выделить:
1. Модели со стоимостными характеристиками (определение требуемой интенсивности обслуживания или оптимального количества параллельных сервисов). Требуется найти компромисс между затратами на обслуживание и потерями, связанными с задержками в предоставлении услуг или отказами в обслуживании.
2. Модели предпочтительного уровня обслуживания. Необходимо уравновесить два конфликтующих показателя: среднее время нахождения заявки в системе (в очереди) и коэффициент простоя каналов обслуживания.
2. Как рассчитать функциональные характеристики работы СМО на основе результатов имитационного моделирования?
Рассмотрим следующий пример:

Функциональные характеристики работы СМО на основе результатов имитационного моделирования рассчитываются следующим образом:
В области QUEUES представлены показатели моделирования изменения очереди. Очередь Q1 имеет максимально допустимую емкость (CAPACITY), равную 4. Средняя длина очереди (AV. LENGTH) составила 2,14 заявки. В столбце MIN/MAX/LAST LEN отображены соответственно минимальная (0), максимальная (4) и последняя (3) длины очереди. Среднее время ожидания заявкой своего обслуживания (AV.DELAY (ALL)) составило 0,58 мин. Этот показатель относится ко всем заявкам, включая те, которые не стояли в очереди. Для тех же заявок, которые стояли в очереди, среднее время ожидания (AV.DELAY (+VE WAIT)) составило 0,69 мин. Доля заявок, которым не пришлось стоять в очереди, указана в последнем столбце (%ZERO WAIT TRANSACTION) и составляет 17%. Приведены также среднекрадратичные отклонения описанные параметров и 95% доверительный интервал.
В области FACILITIES отражены свойства узлов обслуживания. В моделируемой СМО имеется 2 параллельно работающих сервиса (NBR SRVRS). Количество занятых каналов изменялось от 0 до 2, а в момент окончания имитации оба канала также были заняты (столбец MIN/MAX/LAST UTILZ). Столбец AV.UTILIZ показывает среднее количество занятых средств обслуживания (1,8453). Два последних столбца отражают информацию о средней продолжительности периодов простоя (AV.IDLE TIME) и занятости (AV.BUSY TIME) сервиса. Средняя продолжительность занятости не может быть меньше продолжительности обслуживания. Поскольку среднее время обслуживания одной заявки составляет 0,5 мин., а среднее время занятости 3,11 мин., то получаем, что каждый сервис обслуживает приблизительно 3,11 / 0,5 = 6,22 клиента, а затем простаивает 0,26 мин.
В области TRANSACTION COUNT приведена информация о движении потока заявок в имитационной модели. В нашем случае за 599,6 мин., в систему поступило 3003 заявки на обслуживание. Из них 763 были удалены из системы по причине отказа в обслуживании (исчерпана максимально допустимая емкость очереди). Из оставшихся 2240 заявок 380 избежали ожидания в очереди, а 1860 были вынуждены ожидать начала обслуживания в силу занятости средств обслуживания. В момент окончания сеанса моделирования в очереди оставалось еще 3 заявки. На вход узла обслуживания F1 поступило 2237 заявок. Из них 2235 были полностью обслужены, а 2 остались в процессе обслуживания на момент окончания имитации.
Таким образом, среди основных характеристик описываемой СМО можно выделить следующие.
Таблица 3.1
| Характеристика | Значение |
| l | 1/0,2 = 5 пок./мин. |
| m | 1/0,5 = 2 пок./мин. |
| с | 2 |
| время моделирования | 599,6 мин. |
| общее количество заявок | 3003 пок. |
| количество отказов в обслуживании | 763 пок. |
| количество обслуженных заявок | 3003 – 763 = 2240 |
| pотк | 763/3003 = 0,254 (25,4%) |
| q | 1 – 0,254 = 0,746 (74,6%) |
| эфф | 2240/599,6 = 3,74 пок./мин. |
| Lq | 2,14 пок. |
| Wq | 0,58 мин. |
Вывод: я научилась определять функциональные характеристики системы массового обслуживания на основе имитационного моделирования; приобрела опыт синтеза систем массового обслуживания с заданными характеристиками.
Похожие работы
... 2-3 Поиск литературы 7 1 7 2-4 Разработка модели разветвленной СМО 6 1 6 3 Поиск литературы завершен 3-6 Изучение литературы по теории массового обслуживания 10 1 10 4 Модель разработана 4-5 Разработка алгоритма программы 10 1 10 5 Алгоритм программы разработан 5-7 Выбор среды программиро-вания и создание программы 30 1 ...
... цикла 2.1.: "}". 3. Завершение процесса моделирования: 3.1. Вывод результатов моделирования. 2.4 Разработка программной реализации алгоритма В данном разделе мы разрабатываем программную реализацию имитационного моделирования работы Парикмахерской. Помимо общих переменных, которые были описаны выше в п.2.3., в этом разделе можно описать и частные переменные, которые используются в программе ...
... возвращаются на ввод и во всех очередях обслуживаются первыми. Смоделировать работу вычислительного центра в течение 30 ч. Определить необходимую емкость буферов и функцию распределения времени обслуживания заданий. 1.1 Построение концептуальной модели объекта На первом этапе проведения моделирования необходимо построить концептуальную модель (Рис. 1), т.е. концептуальная (содержательная) ...
... из одного состояния в другое и распределение времени пребывания процесса в каждом состоянии (в виде функции распределения F(t) или в виде плотности распределения f(t)) Классификация систем массового обслуживания В общем случае СМО классифицируется по следующим признакам: · закону распределения входного потока · числу обслуживающих приборов · закону распределения времени обслуживания в ...
0 комментариев