ЛАБОРАТОРНАЯ РАБОТА
Математическое моделирование работы систем массового обслуживания
Задание
Вариант 1. Газозаправочная станция для автомобилей располагает двумя газовыми насосами. В очереди, ведущей к насосам, могут расположиться не более пяти автомашин, включая те, которые обслуживаются. Если уже нет места, прибывающие автомобили уезжают искать другую заправку. Распределение прибывающих автомобилей является пуассоновским с математическим ожиданием 20 автомобилей в час. Время обслуживания клиентов имеет экспоненциальное распределение с математическим ожиданием 6 минут.
На основе расчета функциональных характеристик СМО определить:
– процент автомобилей, которые будут искать другую заправку;
– процент времени, когда используется только один из насосов;
– процент времени использования двух насосов;
– вероятность того, что прибывающий автомобиль найдет свободное место в очереди;
– среднее время пребывания автомобиля на газозаправочной станции.
массовый обслуживание транспорт автомобильный
Функциональные характеристики СМО
| Характеристика | Описание | Значение |
| l | интенсивность входного потока заявок | 20 |
| m | интенсивность обслуживания | 10 |
| | относительная нагрузка на систему | 2,00000 |
| эфф | эффективная интенсивность поступления заявок в систему | 13,3333 |
| Lq | среднее число заявок в очереди | 2,00000 |
| Ls | среднее число находящихся в системе заявок | 3,73333 |
| Wq | средняя продолжительность пребывания заявки в очереди | 0,11538 |
| Ws | средняя продолжительность пребывания заявки в системе | 0,21538 |
| p0 | вероятность состояния S0 | 0,06667 |
| p1 | вероятность состояния S1 | 0,13333 |
| P2 | вероятность состояния S2 | 0,13333 |
| P3 | вероятность состояния S3 | 0,13333 |
| P4 | вероятность состояния S4 | 0,13333 |
| P5 | вероятность состояния S5 | 0,13333 |
| P6 | вероятность состояния S6 | 0,13333 |
| P7 | вероятность состояния S7 | 0,13333 |
Интерпретация полученных результатов.
– процент автомобилей, которые будут искать другую заправку = pc+m = p7 = 13,33%
– процент времени, когда используется только один из насосов = p1 = 13,33%
– процент времени использования двух насосов = p2 + … +p7 = 80%
– вероятность того, что прибывающий автомобиль найдет свободное место в очереди = 1 – p7 = 86,67%
– среднее время пребывания автомобиля на газозаправочной станции = Ws = 0,21538 ч. = 13 минут
Контрольные вопросы:
1. Из каких основных компонентов состоит СМО?
Системы массового обслуживания (СМО) – это такие системы, в которые в случайные моменты времени поступают заявки на обслуживание, которые удовлетворяются с помощью имеющихся в распоряжении системы каналов обслуживания (сервисов).
Основными компонентами СМО являются два потока событий:
1) входной поток заявок (требований на обслуживание), характеризующийся своей интенсивностью l (средним количеством клиентов, поступающих в систему в единицу времени) или средним интервалом времени между их последовательными поступлениями tпост;
2) выходной поток заявок, описываемый интенсивностью обслуживания m (средним количеством обслуженных заявок в единицу времени) или средней продолжительностью обслуживания tобсл.
Для СМО разомкнутого типа, у которых входной и выходной потоки подчинены распределению Пуассона, в качестве исходных данных для расчета функциональных характеристик используются:
· интенсивность входного потока заявок l;
· интенсивность обслуживания m;
· количеством параллельно работающих однородных сервисов (обслуживающих каналов) с;
· максимальная емкость очереди m;
· мощность источника заявок f.
2. Какие бывают СМО?
Состоянием системы называется число находящихся в данный момент в СМО заявок n. Поступающие заявки могут сразу попасть на обслуживание (если сервис свободен) или ожидать в очереди.
Если максимально допустимое число мест в очереди m конечно, то в СМО могут происходить отказы в предоставлении сервиса (система с отказами). Отклоняются от обслуживания те заявки, в момент прихода которых все места в очереди случайно оказались занятыми или при m = 0 (система без очереди) все каналы обслуживания оказались занятыми. В СМО с неограниченной длиной очереди (m = ¥) пришедшая заявка при невозможности немедленного обслуживания ожидает обслуживания при любой длине очереди и продолжительности времени ожидания.
По способу отбора из очереди заявок для обслуживания различают следующие виды дисциплины очереди:
1) первым пришел – первым обслуживается (FCFS);
2) последним пришел – первым обслуживается (LCFS);
3) случайный отбор заявок (SIRO);
4) ограничено время пребывания заявки в очереди;
5) с приоритетами, при которой некоторые находящиеся в очереди заявки имеют право первоочередного обслуживания (например, срочные работы выполняются раньше обычных).
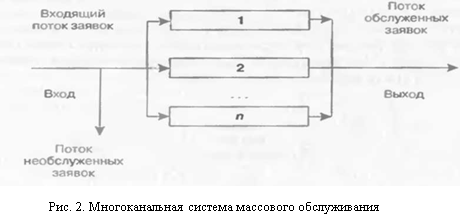
По числу каналов обслуживания c различают одноканальные и многоканальные СМО. Многоканальные СМО разделяют:
· по характеристикам каналов – на однородные и неоднородные СМО;
· по расположению каналов – на СМО с параллельным и последовательным расположением сервисов.
В некоторых СМО интенсивность входного потока может зависеть от числа заявок, уже находящихся в системе (СМО замкнутого типа). В такой системе конечность очереди является следствием ограниченности мощности источника, создающего заявки на обслуживание. В СМО с источником бесконечной мощности (СМО разомкнутого типа) интенсивность входного потока практически не зависит от состояния системы.
3. Как определить основные функциональные характеристики СМО?
Наиболее употребляемыми функциональными характеристиками стационарных СМО являются следующие:
· pотк – вероятность отказа в обслуживании (средняя доля заявок, получивших отказ в обслуживании):
– для СМО с отказами
![]() ;
;
– для СМО с неограниченной очередью
pотк = 0;
· q – относительная пропускная способность системы (средняя доля обслуженных заявок; вероятность обслуживания)
q = 1 – pотк;
· – относительная нагрузка на систему
r = l / m;
· эфф – эффективная интенсивность поступления заявок в систему (абсолютная пропускная способность системы; среднее число заявок, обслуживаемых системой в единицу времени)
· Lq – среднее число заявок в очереди (средняя длина очереди):
– для СМО без очереди
Lq = 0;
– для СМО с ограниченной очередью

– для СМО с неограниченной очередью
![]() ;
;
· Ls – среднее число находящихся в системе заявок
· Wq – среднее время (средняя продолжительность) пребывания заявки в очереди
· Ws – среднее время (средняя продолжительность) пребывания заявки в системе
· ![]() – среднее количество занятых средств обслуживания
– среднее количество занятых средств обслуживания
![]() ;
;
· pn – вероятность того, что в системе находится n заявок
– для СМО с отказами
![]() ;
; 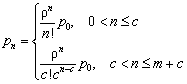 ;
;
– для СМО с неограниченной очередью
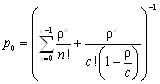 ;
;
В ходе работы я научилась определять количественные показатели качества функционирования системы массового обслуживания.
Похожие работы
... из одного состояния в другое и распределение времени пребывания процесса в каждом состоянии (в виде функции распределения F(t) или в виде плотности распределения f(t)) Классификация систем массового обслуживания В общем случае СМО классифицируется по следующим признакам: · закону распределения входного потока · числу обслуживающих приборов · закону распределения времени обслуживания в ...
... 2-3 Поиск литературы 7 1 7 2-4 Разработка модели разветвленной СМО 6 1 6 3 Поиск литературы завершен 3-6 Изучение литературы по теории массового обслуживания 10 1 10 4 Модель разработана 4-5 Разработка алгоритма программы 10 1 10 5 Алгоритм программы разработан 5-7 Выбор среды программиро-вания и создание программы 30 1 ...
... остальных состояний системы. В результате получим систему уравнений: Решение этой системы будет иметь вид: (4) , ,…, (5) 4. Основные понятия и классификация систем массового обслуживания Заявкой (или требованием) называется спрос на удовлетворение какой-либо потребности (далее потребности предполагаются однотипными). Выполнение ...
... вопросы должны быть получены в ходе маркетинговых и проектно-изыскательских работ на фазе проектирования спортивных сооружений. И уже на этой стадии в процесс активно включаются экономико-математические методы, задействуется существующий аппарат математического моделирования и прогнозирования. Данные методы и расчеты совершенно необходимы для определения: сроков окупаемости отдельных предприятии ...
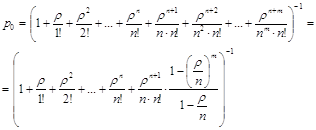
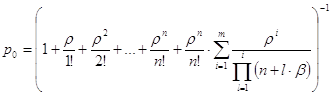
0 комментариев