Изучение методов расчета стационарных режимов работы линейных электрических цепей

Содержание

Введение

1. Цепь постоянного тока

2. Цепь при гармоническом воздействии

3. Переходные процессы в цепях первого порядка

4. Определение реакции цепи на произвольное внешнее воздействие

Заключение

Список литературы

Введение

Цель курсовой работы состоит в изучении методов расчета стационарных режимов работы линейных электрических цепей, переходных процессов в них и расчете реакции цепи на внешнее воздействие произвольной формы.

Техническое задание

В процессе выполнения работы необходимо:

1. При воздействии на цепь источников постоянного тока и напряжения определить токи во всех ветвях схемы, методами наложения и узловых напряжений; законами Ома и Кирхгофа определить напряжения на каждом элементе схемы. Проверить правильность расчета схемы, составив уравнение баланса мощности.

2. При воздействии на цепь источников гармонического колебания определить токи во всех ветвях схемы методом контурных токов; законами Ома и Кирхгофа определить напряжения на каждом элементе схемы. В конденсаторе C₁ определить ток методом эквивалентного генератора. Проверить правильность расчета схемы с помощью законов Кирхгофа, составить уравнение баланса мощности активных и реактивных мощностей.

3. Анализируя переходные процессы в цепи первого порядка, определить закон изменения выходного напряжения E, а также при отключении резистора R^* . Построить соответствующие графики.

4. Рассчитать и построить график напряжения на входе цепи U₂ (t) частотным методом, если на вход цепи действует сигнал U₁ (t).

Часть 1. Цепь постоянного тока.

1.1 Проведем полный анализ работы цепи при воздействии источников постоянного напряжения и тока.

При протекании постоянного тока через индуктивный элемент, индуктивность эквивалентна короткозамкнутому участку цепи, а емкость дает разрыв цепи.

Тогда получим схему:

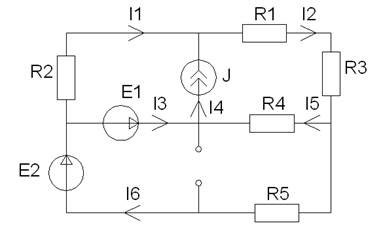
Рисунок 1 - Эквивалентная схема при воздействии источников постоянного тока.

Исходные данные:

E1=50 B; E2=90 B; J=10мА; R1=2кОм; R2=2кОм; R3=2 кОм; R4=3 кОм; R5=6 кОм

1.1.1 Рассчитать схему методом наложения.

В его основе этого метода лежит принцип суперпозиции: если в линейную цепь включены несколько источников напряжения или тока, то реакция цепи равна сумме реакций от каждого источника в отдельности. Составим частичные схемы:

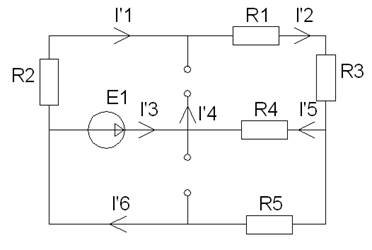
Рисунок 2 - Первая частичная схема

Итак, токи в первой частичной схеме равны:

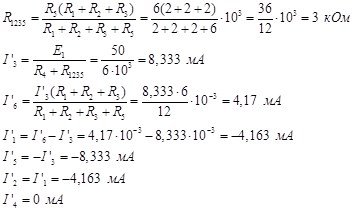
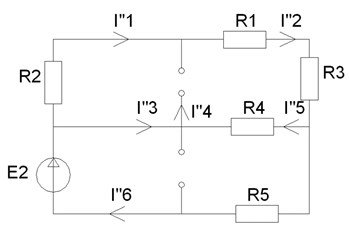
Рисунок 3 - Вторая частичная схема

Итак, токи в второй частичной схеме равны:

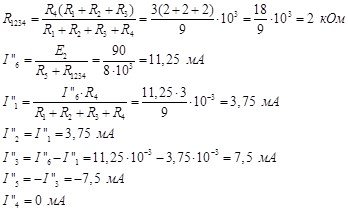
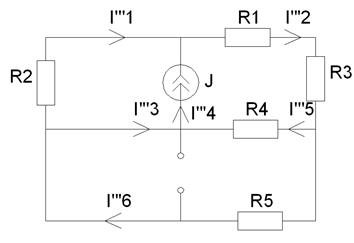
Рисунок 4 - Третья частичная схема

Итак, токи в третьей частичной схеме равны: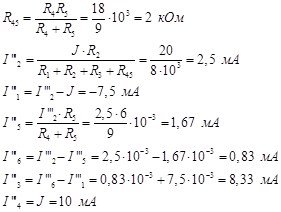

Определим токи в исходной схеме:

1.1.2 Рассчитать схему методом узловых напряжений

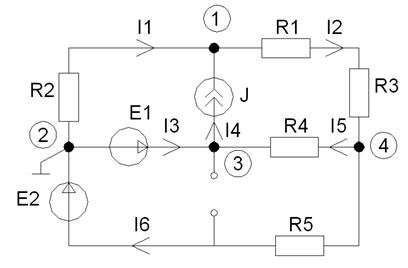
Рисунок 5 - Схема для определения напряжений

Примем второй узел за базисный, тогда:

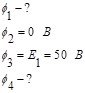
Уравнения для потенциалов:

Уравнения для токов:

1.2 Определение напряжений на каждом элементе схемы.

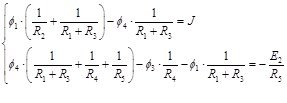
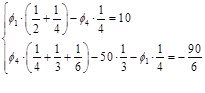
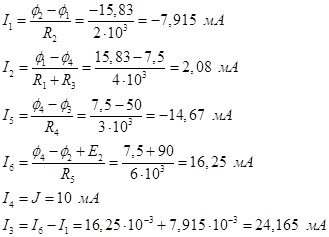
Запишем все рассчитанные токи и напряжения в цепи

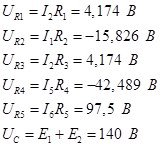
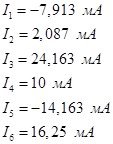
1.3. Проверка балансом мощности.

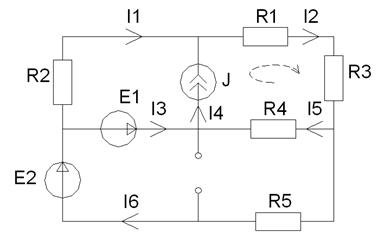
Рисунок 6–Исходная схема

Рассчитаем мощность источников тока и напряжения:

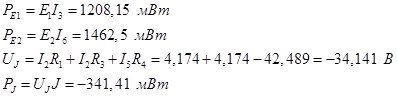
Баланс мощности:

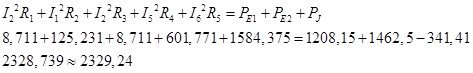
Равенство мощностей источников и потребителей также свидетельствует о правильности расчетов электрической цепи.

Полученные результаты сведем в таблицу:

Таблица 1: Результаты анализа электрической цепи при воздействии постоянных источников энергии:

Параметры Элементы	Ток, мА	Напряжение, В	Мощность, мВт
R1	2,087	4,174	8,711
R2	-7,913	-15,826	125,231
R3	2,087	4,174	8,711
R4	-14,163	-42,489	601,771
R5	16,25	97,5	1584,375
L1	16,25	0	0
L2	16,25	0	0
C	0	140	0
E1	24,163	50	1208,15
E2	16,25	90	1462,5
J	10	-34,174	-341,74

Часть 2. Цепь при гармоническом воздействии

Проведем полный анализ реакции линейной цепи на гармонические воздействия.

E1=50 B; E2=90 B; J=10мА; R1=2кОм; R2=2кОм; R3=2 кОм; R4=3 кОм; R5=6 кОм

L₁=159 мГн; L₂=79,5мГн;М=15,9 мГн; С=1,99 нФ.

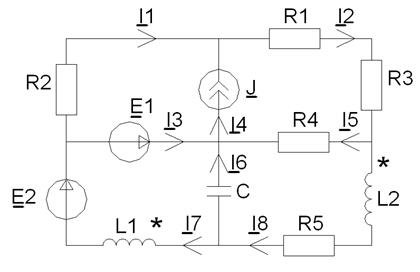
Рисунок 7 - Схема цепи при гармоническом воздействии

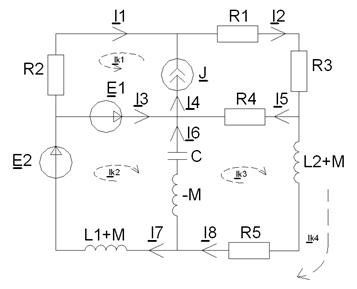
Рисунок 8 - Схема цепи после «развязки» индуктивных связей

Определим сопротивления реактивных элементов:

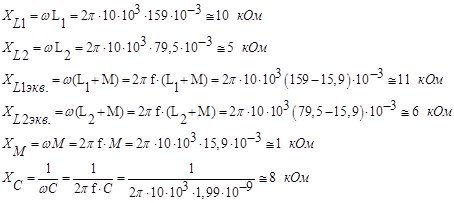
Источники энергии в символической форме записи:

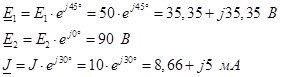
2.1. Находим токи во всех ветвях схемы методом контурных токов.

В основе этого метода лежит введение в каждый контур условного контурного тока, направление которого обычно выбирают совпадающим с направлением обхода контура.

Контурный ток, протекающий по ветви с источником тока, полностью определяется током источника тока:

Составим систему уравнений для метода контурных токов:

 

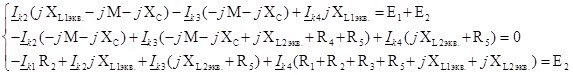
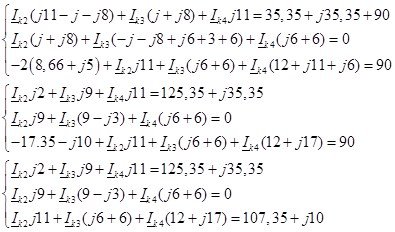
Найдем контурные токи используя правило Крамера:

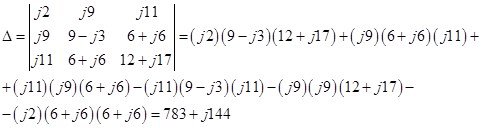
Где-главный определитель системы.

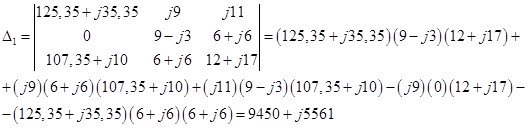
-определители, полученные путём замены в главном определителе первого, второго и третьего столбца на столбец свободных членов:

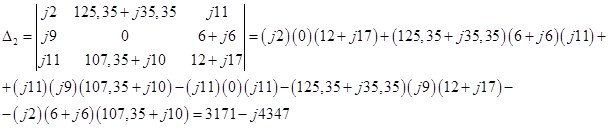
Тогда контурные токи равны:

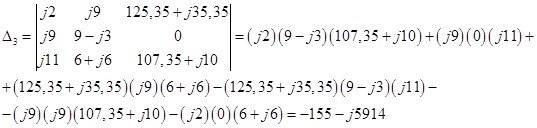
Зная контурные токи, находим токи в ветвях цепи используя принцип наложения:

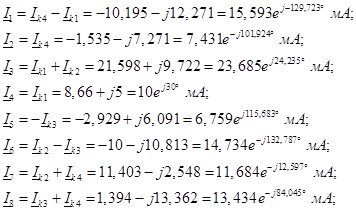
2.2 Определить ток в индуктивности методом эквивалентного генератора.

Исключим конденсатор С из ветви и рассчитаем внутренне сопротивление относительно зажимов а и б:

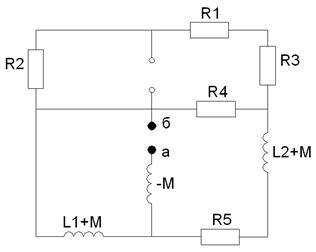
Рисунок 9 - Схема для определения

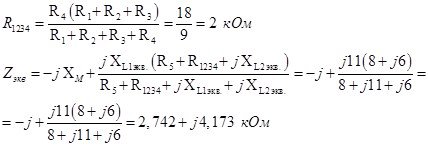
Определим напряжение Uxx, которое равно напряжению активного двухполюсника на зажимах а - б режиме холостого хода (рисунок 12):

Рисунок 10– Схема для определения Uxx

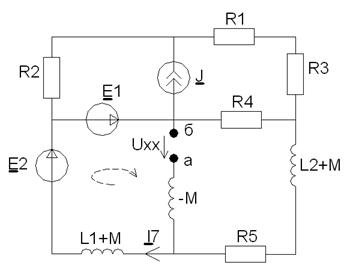
Составим уравнение по второму закону Кирхгофа для контура, обозначенного на рисунке 12:

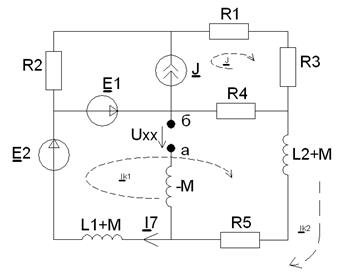
Рисунок 11 - Схема для определения тока

Найдем контурные токи используя правило Крамера:

Где-главный определитель системы.

-определители, полученные путём замены в главном определителе первого, второго и третьего столбца на столбец свободных членов:

 

 

Тогда контурные токи равны:

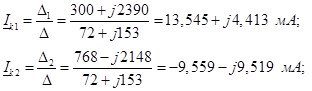
Тогда ток равен:

:

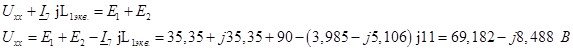Напряжение холостого хода:

Ток в конденсаторе:

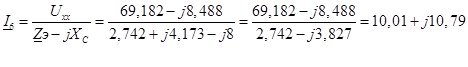
Сравнивая полученные результаты тока , с результатами, полученными в методе контурных токов, видно, что результаты вычислений идентичны, что говорит о правильности проведенных расчетов.

2.3 Определение напряжений на элементах цепи.

Определим напряжения на пассивных элементах цепи, используя закон Ома:

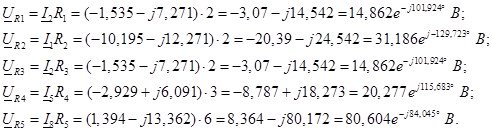
Определим напряжения на реактивных элементах цепи. Так как индуктивно связанные катушки включены согласно, то напряжение на них:

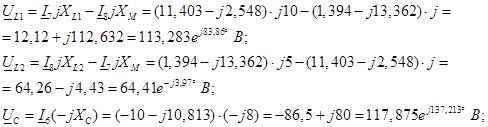
Напряжение на источнике тока с помощью второго закона Кирхгофа:

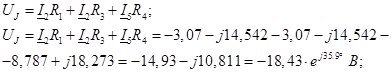
Проверить правильность расчетов токов и напряжений можно с помощью законов Кирхгофа.

2.4 Проверка правильности расчета схемы методом законов Кирхгофа

Составим систему уравнений по законам Кирхгофа:

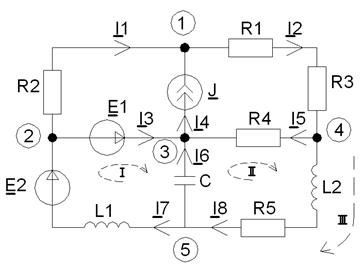
Рисунок 12 - Схема для составления законов Кирхгофа

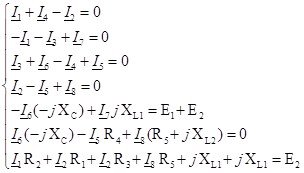
Подставим в полученную систему уравнений рассчитанные значения токов и напряжений:

Подставляя в полученную систему уравнений рассчитанные значения токов и напряжений, получаем выполнение равенств всех уравнений, что свидетельствует о правильности выполненных расчетов.

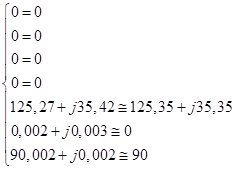
2.5 Баланс мощности

Сумма комплексных мощностей, отдаваемых независимыми источниками энергии равна сумме комплексных мощностей, потребляемых остальными элементами электрической цепи.

S=P+jQ – полная комплексная мощность, мВА;

P- активная мощность, мВА;

Q – реактивная мощность, мВА.

Определим полную комплексную мощность, отдаваемую источниками в цепь:

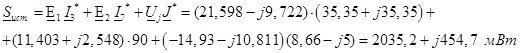
Определим активную мощность, рассеиваемую в резисторах схемы:

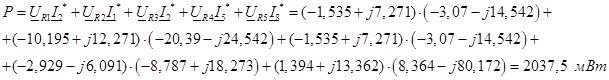
Определим реактивную мощность:

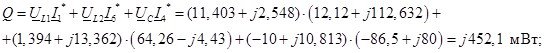
Полная комплексная мощность, потребляемая пассивными элементами цепи:

что практически полностью соответствует комплексной мощности, отдаваемой источниками энергии.

Полученные результаты сведем в таблицу:

Таблица 2 - Результаты анализа электрической цепи при воздействии синусоидальных источников энергии:

Параметры Элементы	Ток, мА	Напряжени, В	Мощность, мВА
R1			110,44
R2			486,28
R3			110,44
R4			137,05
R5			1082,83
L1			j1323,6
L2			j865,28
C			-j1736,77
E1
E2		90
J

Часть 3. Переходные процессы в цепях первого порядка.

3.1 Расчет напряжения на выходе цепи при замыкании в цепь источника постоянного напряжения Е в момент времени t=0 мс.

3.1.1 Первый случай (R* подключено):

E=12 B; L=1 Гн; R=1 кОм.

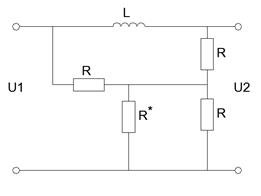
Рисунок 13 - Исходная схема

Итак, в момент времени t=0- мс исходная схема принимает вид:

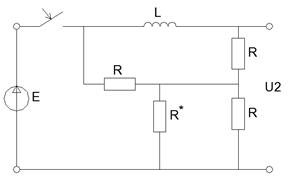
Рисунок 14 - Схема непосредственно перед коммутацией ключа

Так как в схеме нет источника энергии (источник постоянного напряжения еще не подключен к цепи), токи в схеме отсутствуют, а, следовательно, выходное напряжение равно нулю.

Начальное условие в цепи: UL(0+)=UL(0-).

В момент коммутации согласно закону коммутации, индуктивность ведет себя как холостой ход [1], тогда:

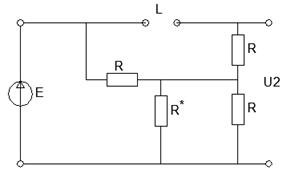
Рисунок 15 - Схема непосредственно после коммутации ключа

В этой схеме выходное напряжение цепи равно:

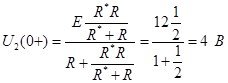
В установившемся режиме после коммутации клоню индуктивность представляет собой короткозамкнутый провод (цепь постоянного тока), и принимает вид:

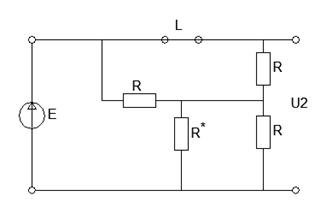
Рисунок 16 - Схема в установившемся режиме после коммутации ключа

Выходное напряжение равно входному напряжению:

Определим корень характеристического уравнения:

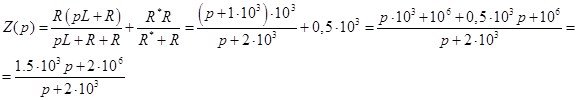
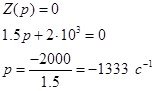
Закон изменения выходного напряжения:

3.1.2 Второй случай (R* отключено):

В этом случае закон изменения выходного напряжения определим операторным методом. Переходный процесс в возникает вследствие отключения резистора R*, т.е.:

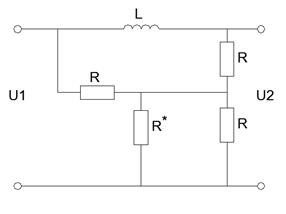
Рисунок 17 - Исходная схема

Для того, чтобы изобразить схему замещения, необходимо определить независимое начальное условие (ток в катушке индуктивности непосредственно до коммутации ключа).

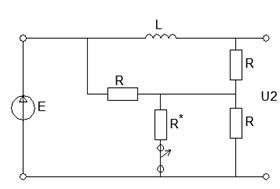
Рисунок 18 - Схема непосредственно перед коммутацией ключа

Такая цепь уже была рассчитана (см. первый случай), поэтому:

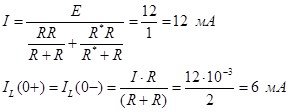
Следовательно, операторная схема замещения с учетом ННУ [2]:

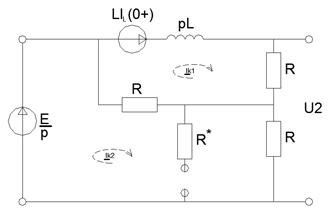
Рисунок 19 - Операторная схема замещения

Найдем изображение выходного напряжения рассчитав операторную схему методом контурных токов:

Приравняем знаменатель изображения выходного напряжения к нулю и найдем полюсы функции F(р):

Найдем производную F’2(р):

Подставим полученные полюсы в F1(р) и F2’(p):

Тогда оригинал выходного напряжения согласно теореме разложения:

Таким образом, выходное напряжение U2(t):

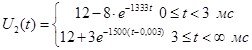
Определим постоянные времени т для каждого случая:

Таблица 3 - Значения выходного напряжения:

t, мс		U2(t), В	t, мс		U2(t), В
0	0	4	3+	3+	15
0,5τ1	0.375	7.147	3+0,5τ2	3,335	13.815
τ1	0.75	9.056	3+τ2	3,67	13.098
1,5τ1	1.125	10.214	3+1,5τ2	4,005	12.664
2τ1	1.5	10.917	3+2τ2	4,34	12.402
2,5τ1	1.875	11.343	3+2,5τ2	4,675	12.243
3τ1	2.25	11.601	3+3τ2	5,01	12.147
3,5τ1	2.625	11.758	3+3,5τ2	5,345	12.089
3-	3-	11.853	∞	∞	12

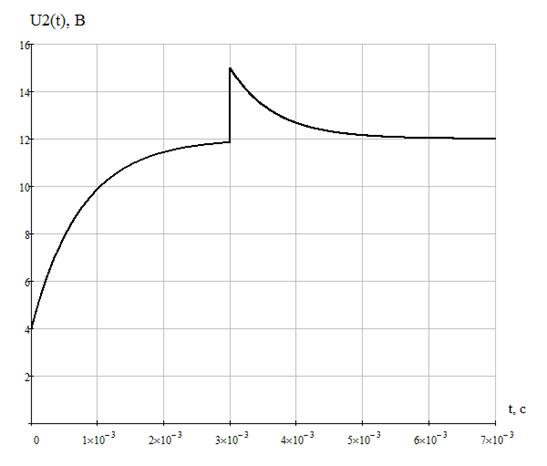
Рисунок 24 - График выходного напряжения

Часть 4. Определение реакции цепи на произвольное внешнее воздействие.

4.1 Определить системные характеристики цепи:

4.1.1 Определение переходной характеристики g(t).

Цепь до момента коммутации. t(0-)

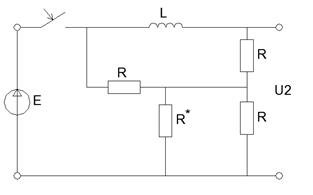
Рисунок 20 - Схема непосредственно перед коммутацией ключа

[В]

Цепь в момент, коммутации. t(0+)

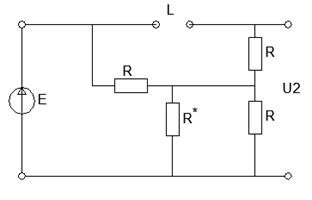
Рисунок 21 - Схема непосредственно после коммутацией ключа

По закону коммутации напряжение на катушке скачком измениться не может

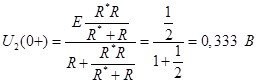
В установившемся режиме. t(∞)

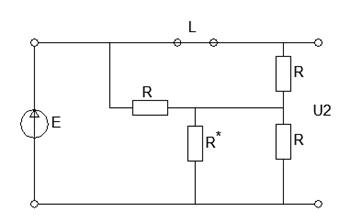
Рисунок 22 - Схема в установившемся режиме

Выходное напряжение равно входному напряжению:

Определим корень характеристического уравнения:

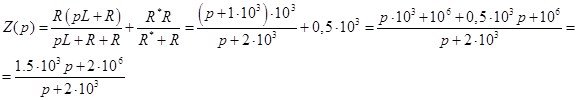
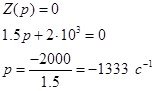
Тогда переходная характеристика равна:

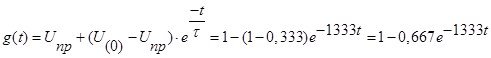
Таблица 4 – Переходная характеристика цепи

t, мс		g(t)
0	0	0.333
0,5τ	0.375	0.595
τ	0.75	0.755
1,5τ	1.125	0.851
2τ	1.5	0.91
2,5τ	1.875	0.945
3τ	2.251	0.967
3,5τ	2.626	0.98
4τ	3.001	0.988

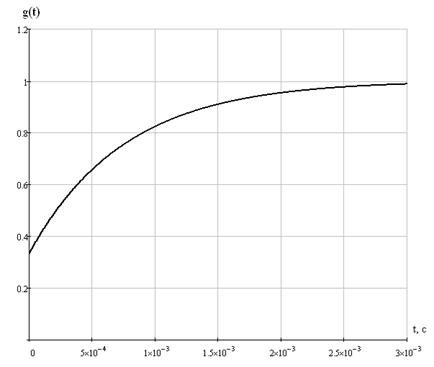
Рисунок 23 - Переходная характеристика цепи

4.1.2 Определение импульсной характеристики h(t).

Временные и частотные характеристики цепи связаны между собой формулами преобразования Фурье. По найденной переходной характеристике вычисляется импульсная характеристика цепи.

где

Таблица 5 – Импульсная характеристика цепи

t, мс		h(t)
0	0	889.111
0,5τ	0.375	539.273
τ	0.75	327.086
1,5τ	1.125	198.387
2τ	1.5	120.328
2,5τ	1.875	72.983
3τ	2.251	44.266
3,5τ	2.626	26.849
4τ	3.001	16.285

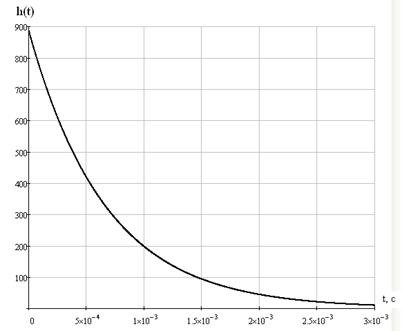
Рисунок 24 - Импульсная характеристика цепи

4.1.3 Определение КПФ цепи.

Передаточная характеристика цепи – это отношение изображения выходной реакции цепи к изображению входного воздействия.

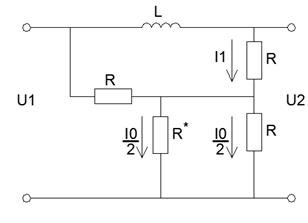
Рисунок 23 - Исходная цепь

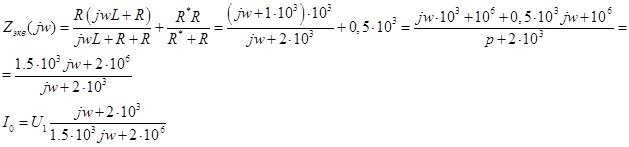
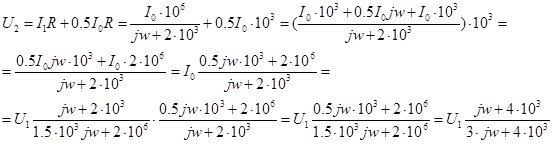
Амплитудно-частотная характеристика (АЧХ) этой цепи равна:

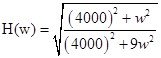
Фазо-частотная характеристика (ФЧХ) цепи равна:

Таблица 6 – Частотные характеристики цепи

f, кГц	H(f)	φ(f), град	f, кГц	H(f)	φ(f), град
0	1	0	1,6	0.356	-14.142
0,2	0.763	-25.863	1,8	0.351	-12.754
0,4	0.553	-29.911	2	0.348	-11.6
0,6	0.458	-27.219	2,2	0.345	-10.629
0,8	0.412	-23.656	2,4	0.344	-9.803
1	0.387	-20.501	2,6	0.342	-9.092
1,2	0.372	-17.918	2,8	0.341	-8.475
1,4	0.362	-15.834	3	0.34	-7.935

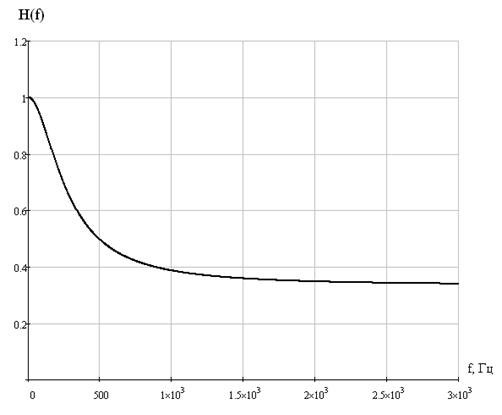
Рисунок 26 – Амплитудно-частотная характеристика цепи

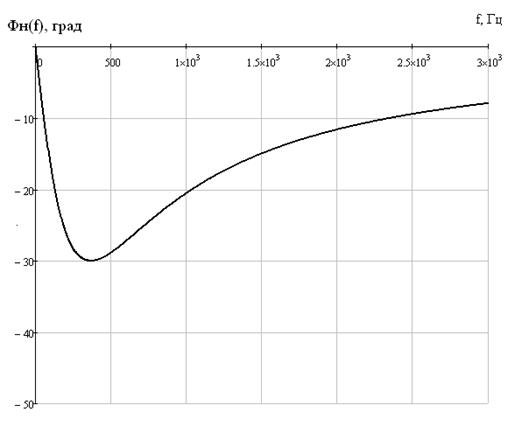
Рисунок 27 – Фазо-частотная характеристика цепи

4.2Спектральным методом рассчитать и построить график напряжения на выходе цепи U2(t), если на её вход подается сигнал U1(t).

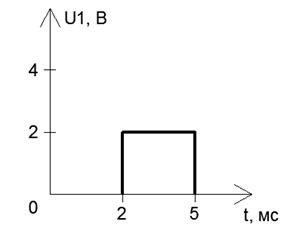
Рисунок 24 – Сигнал на входе цепи

Для нахождения спектральной плотности входного сигнала функция U1(t) представляется в виде суммы «простейших» функций.

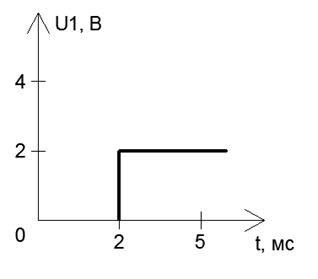
Рисунок 25 – Первая простейшая функция сигнала U1(t)

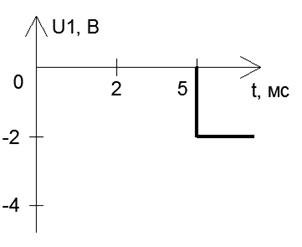
Рисунок 26 – Вторая простейшая функция сигнала U1(t)

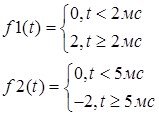
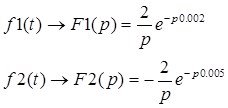
Запишем преобразование Лапласа для входного сигнала:

F(p)=F1(p)+F2(p)

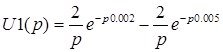
Запишем преобразование Лапласа для исходной цепи:

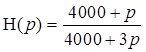
Зная спектр входного сигнала найти выходной сигнал как функцию от времени. Используем обратное преобразование Лапласа.

Таблица 4 - Значения выходного напряжения:

t, мс	0	1	2-	2+	2,5	3	3,5	4	4,5	5-	5+
U2, B	0	0	0	0,667	1,316	1,649	1,82	1,907	1,952	1,976	1,309
t, мс	5,5	6	6,5	7	7,5	8	8,5	9	8,5	10
U2, B	0,672	0,345	0,177	0,091	0,047	0,024	0,012	0,006	0,003	0,002

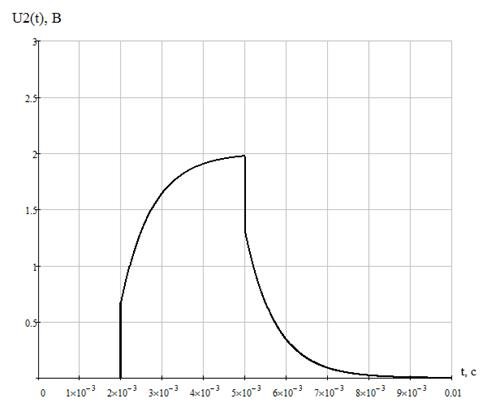
Рисунок 27 - График зависимости выходного сигнала от времени

Заключение

В результате выполнения курсовой работы произведены расчеты стационарных режимов работы линейных электрических цепей, переходных процессов и реакции цепи на внешнее воздействии произвольной формы.

При воздействии на цепь источников постоянного тока и напряжения определенны токи во всех ветвях схемы, методами наложения и узловых напряжений; законами Ома и Кирхгофа определены напряжения на каждом элементе схемы. Также проверена правильность расчета схемы, на основе составления уравнения баланса мощности.

При воздействии на цепь источников гармонического колебания определены токи во всех ветвях схемы методом контурных токов; законами Ома Кирхгофа определены напряжения на каждом элементе схемы. В конденсаторе С₁ определен ток методом эквивалентного генератора. Также проверена правильность расчета схемы с помощью законов Кирхгофа, составления уравнения баланса мощности активных и реактивных мощностей.

Анализируя переходные процессы в цепи первого порядка, определен закон изменения выходного напряжения U₂(t) при замыкании на цепь источника постоянного напряжения E, а также при отключении резистора R*. Построены соответствующие графики.

Был рассчитан и построен график напряжения на выходе цепи U₂(t) частичным методом при воздействии на вход цепи сигнала U₁(t).

Таким образом, поставленные в начале работы цели достигнуты.

Список литературы

1.Бакалов В.П., Дмитриков В.Ф., Крук Б.И. Основы теории цепей. Радио и связь, 2000г.

2.Бакалов В.П., Дмитриков В.Ф., Крук Б.И. Основы анализа цепей, Москва, Горячая линия- Телеком, 2007г.