Автоматы с программируемой логикой

Рассмотренные выше реализации микропрограммного автомата на жесткой логике приводят к различным схемным решениям в зависимости от исходных  ГСА. А это значит, что при изменении функции автомата (изменении ГСА) необходимо изменять либо заново проектировать его схему. Реализация автомата на программируемых матрицах (ПЛМ – однократно программируемых), при незначительных изменениях в алгоритме работы автомата, требует программирования новых ПЛМ. Этого недостатка лишены автоматы с программируемой логикой. Алгоритм функционирования автомата с программируемой логикой представляется в виде закодированной микропрограммы, которая может загружаться в перепрограммируемые постоянные запоминающие устройства (ППЗУ) или в оперативные ЗУ (ОЗУ). Изменения в алгоритме отражаются в микропрограмме, но не влияют на схему автомата.

3.3.1 Принцип управления по хранимой программе

Напомним, что функция микропрограммного управляющего автомата определяется:

- множеством входных сигналов (логических условий): Х = {х₁, х₂ …х _n };

- множеством выходных сигналов (микрокоманд): У = {у₁, у₂ …у _k };

- микропрограммой (ГСА), задающей порядок следования выходных сигналов У в зависимости от значений входных сигналов X.

Если автомат Мура описан прямой таблицей переходов, то для каждого состояния a_m известно:

- множество выходных сигналов У(a_m), вырабатываемых автоматом в состоянии a_m;

- множество входных сигналов Х(a_m), определяющих все возможные переходы автомата из состояния a_m в состояние a_s;

- множество состояний a_s, в которые может перейти автомат из состояния a_m (обозначим A(a_m).

Для каждого состояния автомата Мура (а значит для каждой операторной вершины ГСА) эту информацию, необходимую и достаточную для описания закона функционирования автомата,  можно закодировать и представить двоичным словом (микрокомандой – не путать с выходным сигналом автомата у_i, который часто так же называют микрокомандой !), которое имеет  следующую структуру:

№

уm1

уm2

…

уmk

хm1

хm2

…

хmn

аm1

аm2

…

аms

где:

№ – номер двоичного слова, соответствующего состоянию автомата а_m (или его адрес ЗУ, где будет храниться микропрограмма);

у_mi – выходной сигнал (микрокоманда), который должен вырабатывать автомат в данном состоянии а_m; в общем случае таких сигналов k; эта часть двоичного слова называется операционной;

х_mi – входной сигнал (логическое условие), участвующее хотя бы в одном переходе из a_m в a_s ; в общем случае таких сигналов n; эта часть двоичного слова называется управляющей;

а_mi – одно из состояний а_s , в которое может перейти автомат из состояния а_mпри определенных значениях логических условий х_mi. Поскольку описание одного состояния – это одно двоичное слово, имеющее свой адрес в ЗУ,  а_mi можно считать адресом состояния а_mi в ЗУ; в общем случае таких состояний s. Если количество логических условий в слове равно n, то количество а_mi равно 2 в степени n. Эта часть двоичного слова называется адресной.

Воспользуемся прямой таблицей переходов автомата Мура из примера (п.3.1).

№	a m	a s	Y as	Xa ma s
1 2	a 0	a 0 a 1	y7  y1, y2	Ø x 3 x 3
3 4	a 1	a 2 a 3	y3  y4, y5	x 1 Ø x 1
5	a 2	a 3	y4, y5	1
6 7	a 3	a 4 a 0	y6  y7	Ø x 2 x 2
8 9	a 4	a 2 a 3	y3  y4, y5	x 1 Ø x 1

Если использовать приведенную выше структуру двоичного слова, то для описания данного автомата достаточно пяти двоичных слов (по числу состояний автомата), имеющих следующий формат:

№

уm1

уm2

хm

ах=0

ах=1

Сам номер (№) в слово помещать не нужно, так как это адрес слова в ЗУ. В слове под у_mi отведено два поля, так как максимальное количество у_mi в состоянии а_mравно двум; под х_mi – достаточно отвести одно поле, так как в любом переходе из а_m в а_mi (или а_s) участвует только одно логическое условие. Под а_mi достаточно отвести 2 поля: для адреса перехода при х_m = 0 (а_х=0) и при х_m= 1 (а_х=1). Используя выбранный формат двоичного слова можно составить в виде таблицы содержательную микропрограмму, описывающую работу автомата.

В этой таблице – каждая строка соответствует одному из состояний автомата (столбец a_m); № - соответствует адресу слова, описывающего это состояние в ЗУ. В колонках у_m1 и у_m2 записаны микрокоманды, вырабатываемые автоматом в состоянии a_m, в колонке х_mзаписаны логические условия, определяющие переходы из состояния a_m в состояния, адреса которых в ЗУ записаны в колонках а_х=0 и а_х=1, в колонке  a _m записаны пояснения: какому состоянию автомата соответствует данная строка.

№	уm1	уm2	хm	ах=0	ах=1	a m
0	у7	-	х3	0	1	a 0
1	у1	у2	х1	3	2	a 1
2	у3	-	х3	3	3	a 2
3	у4	у5	х2	4	0	a 3
4	у6	-	х1	3	2	a 4

Каждая из колонок этой таблицы (кроме a_m) должна быть представлена двоичными кодами. Количество двоичных разрядов для каждой колонки можно выбрать таким:

- у_m1 – 3 разряда: здесь будем записывать номер у_m1 (от 1 до 7);

- у_m2 – 3 разряда: здесь будем записывать номер у_m2 (от 1 до 7);

- х_m  – 2 разряда: здесь будем записывать номер х_m (от 1 до 3);

- а_х=0 – 3 разряда: здесь будем записывать адрес а_х=0, по которому в автомате должен произойти переход к следующему слову при х_m =0 (от 0 до 4);

- а_х=1 – 3 разряда: здесь будем записывать адрес а_х=1, по которому в автомате должен произойти переход к следующему слову при х_m =1(от 0 до 4).

Таким образом разрядность двоичного слова в нашем примере равна 14. Закодированная микропрограмма имеет вид, приведенный в таблице. В каждой колонке записаны двоичные числа в соответствии с принятыми выше соглашениями. Требуемый объем памяти – 70 бит. Рассмотрим подробнее 2-ю строку в этих таблицах.

№	уm1	уm2	хm	ах=0	ах=1
0	111	000	11	000	001
1	001	010	01	011	010
2	011	000	11	011	011
3	100	101	10	100	000
4	110	000	01	011	010

В этой и предыдущей таблицах в строке №2 описывается состояние автомата a₂. Из этого состояния – безусловный переход  автомата в состояние a ₃. Поэтому в столбце х_m может быть записан номер любой переменной х_m , а в обоих столбцах а_х=0 и а_х=1 одинаковый адрес перехода. Так как записанный в столбце х_m обязательно имеет одно из значений: 0 или 1, то переход будет безусловным по адресу а_х=0 = а_х=1.

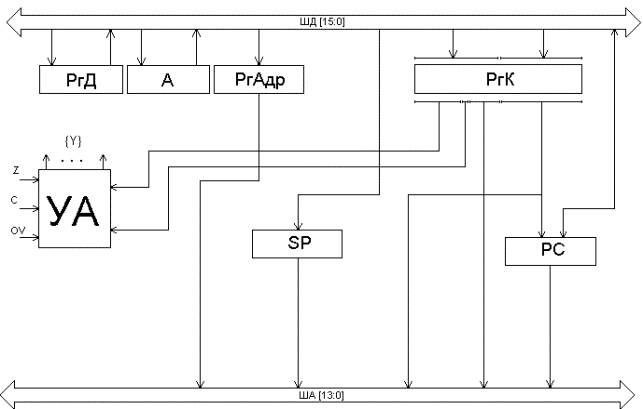
Схема, обеспечивающая работу с закодированной микропрограммой, должна содержать следующие функциональные узлы:

-          память для хранения микропрограммы (ЗУ) объемом не менее пяти слов; чтение слова из памяти осуществляется по адресу, подаваемому на адресный вход ЗУ; разрядность слов – 14 бит;

-          схему, преобразующую двоичный код  у_m1 и у_m2 в унитарный код, соответствующий закодированному у_i; эта схема – дешифратор (DCу);

-          мультиплексор (MSх), выбирающий из множества входных сигналов Х всего один, номер которого записан в столбце х_m;

-          мультиплексор (MSа), выбирающий из слова адрес а_х=0 (если выбранное мультиплексором MSх значение х_m=0) или адрес а_х=1 (если выбранное мультиплексором MSх значение х_m=1);

-          регистр адреса (RG), в который необходимо по импульсу синхронизации записать выбранный мультиплексором MSа адрес и подать его на адресный вход ЗУ, из которого будет считано следующее слово (иначе – переход в следующее состояние).

уm1

уm2

хm

ах=0

ах=1

1

2

3

4

5

6

7

8

9

10

11

12

13

14

Пронумеруем разряды двоичного слова с 1 по 14 (как показано в таблице); номера разрядов будут соответствовать номерам выходов ЗУ.

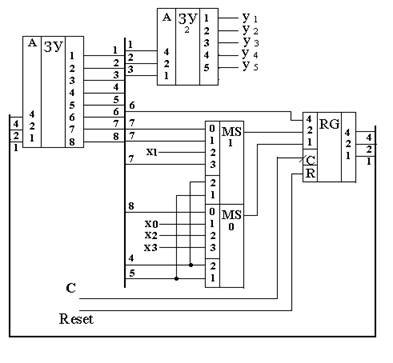
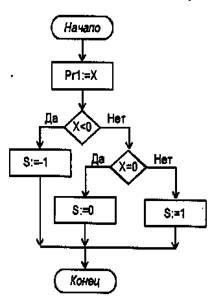
Функциональная схема автомата приведена на рис.27.

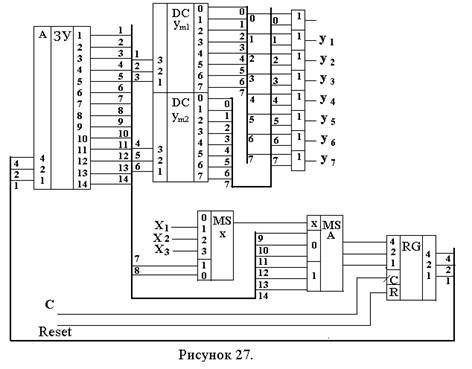
На этой схеме кроме описанных выше элементов имеется 8 дизъюнкторов, объединяющих одноименные выходы дешифраторов DCу_m1 и DCу_m2 . Эти элементы необходимы в случае, если одна и та же микрокоманда у_i будет записана в разных строках микропрограммы в разных столбцах у_m1 и у_m2.

Автомат (рис.27) работает следующим образом. Сигнал Reset=1 устанавливает значение «0» во всех разрядах регистра RG. Код (или двоичное число) А=000 с выхода RG подается на адресный вход ЗУ. На выходах ЗУ (разряды 1..14) появляется слово, записанное по адресу 0 (см. таблицу). В этом слове:

разряды 1,2,3 – подаются на вход DCу_m1 и, поскольку в этих разрядах записано число 111 (7), на выходе «7» DCу_m1 формируется 1, а значит и выходной сигнал у₇ = 1;

разряды 4,5,6 – подаются на вход DCу_m2 и, поскольку в этих разрядах записано число 000 (0), (которое мы не использовали для кодирования у_i) на выходе «0» DCу_m1 формируется «1», но ни на каких либо других выходах у_i эта «1» не появится;

разряды 7,8 – подаются на управляющие входы мультиплексора MSх; в этих разрядах записано число 11 (3). Значение логического условия х₃ появляется на выход MSх;

мультиплексор MSа, в зависимости от значения х₃ («0» или «1») подает на входы регистра адреса RG либо адрес перехода, записанный в разрядах 9,10,11 (если х₃ = 0), либо адрес перехода, записанный в разрядах 12,13,14 (если х₃ = 1);

при поступлении на вход С импульса синхронизации, этот адрес запишется в регистр RG и с его выходов поступит на адресный вход ЗУ, на выходе которого появится слово, записанное по этому адресу.

Таким образом за один цикл (время между синхроимпульсами С) автомат считает из ЗУ некоторое двоичное слово, выработает микрокоманды у_m, проанализирует входные сигналы х_m, и в зависимости от их значения выберет адрес следующего двоичного слова в ЗУ.

Спроектированный нами интуитивно автомат содержит много избыточности и был приведен в качестве примера, как естественное воплощение наших рассуждений. Недостатками такого подхода являются, прежде всего, сложность схемы (при достаточно простых функциях автомата) и не оптимальная длина микрокоманды (двоичного слова), что приводит к неэффективному использованию памяти ЗУ.

Рассмотрим некоторые приемы, позволяющие сделать автомат с программируемой логикой более оптимальным, чем приведенный на рис.27.

Кодирование наборов микроопераций

Выходные сигналы у_i (микрокоманды), вырабатываемые управляющим автоматом, сгруппированы  в операторных вершинах ГСА в виде наборов, инициирующих выполнение операционным автоматом (ОА) совместимых микроопераций. Совместимые микрооперации – это такие, которые могут быть выполнены ОА одновременно.

Пусть автомат должен генерировать nразличных наборов микрокоманд из множества У = {у₁, у₂ …у _k }; обозначим i-ый набор как:

У_i = {у_i1, у_i2 …у_ij }.

Составим матрицу М _N*K, где N – количество различных наборов микрокоманд, а К – количество различных микрокоманд у_i, вырабатываемых автоматом. Элемент матрицы m_ij = 1, если микрокоманда у _j  входит в набор У _i , а если не входит, то m _ij  = 0. Если строки матрицы М (а значит и наборы У_i) не пересекаются, то в операционной части двоичного слова можно обойтись одним полем, в которое записывается номер набора У_i. Этот номер будет подаваться на один дешифратор DCу, на выходе которого будут сформированы микрокоманды у_i.

В нашем примере все микрокоманды у_iможно представить в виде следующих наборов: 

У₀ = {у₇};   У₁ = {у₁, у₂ };    У₂ = {у₃};  У₃ = {у₄, у₅};    У₄ = {у₆}; 

Матрицу М представим в виде таблицы:

	у1	у2	у3	у4	у5	у6	у7
У0							1
У1	1	1
У2			1
У3				1	1
У4						1

Из матрицы видно, что пересечение строк для всех пар У_iи У_j (при i ¹ j) пусто. Закодируем наборы У_i следующим произвольным образом:

К(У₀) = 000;  К(У₁) = 001;  К(У₂) = 010;  К(У₃) = 011;  К(У₄) = 100, 

и  изменим формат микрокоманды:

№

К(Уi)

хm

ах=0

ах=1

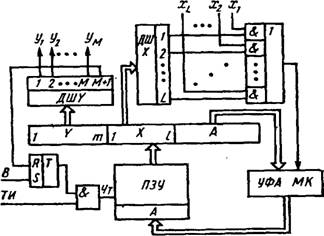
Количество разрядов двоичного слова при этом уменьшится до 11, а значит и уменьшится емкость необходимой памяти ЗУ до 55 бит. Пронумеруем разряды двоичного слова с 1 по 11 (как показано в таблице); номера разрядов будут соответствовать номерам выходов ЗУ на функциональной схеме автомата (рис.28).

К(Уi)

хm

ах=0

ах=1

1

2

3

4

5

6

7

8

9

10

11

Схема на рис.28 незначительно отличается от схемы на рис.27 по своему функционированию. Отличие – один дешифратор микрокоманд У_i, назначение которого описано выше.

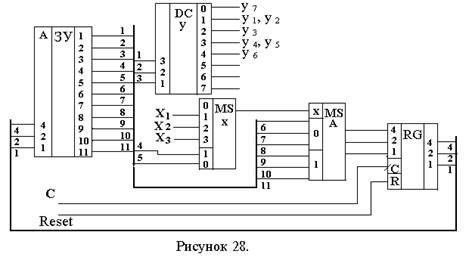
Если наборы микрокоманд в матрице М пересекаются, то описанный в последнем примере подход к их формированию невозможен. Поэтому можно поступить следующим образом.

1.            Если общее количество микрокоманд У_i невелико, то в операционной части двоичного слова можно выделить по одному разряду на каждую микрокоманду. В этом случае отпадает необходимость в дешифраторе DCу, так как в соответствующие разряды операционной части двоичного слова записываются значения (0 или 1) для всех У_i. Таким образом сигналы У_i берутся непосредственно с соответствующих выходов ЗУ. Если использовать такой подход для нашего примера, то разрядность двоичного слова увеличится до 15 бит, емкость ЗУ – до 75 бит, но из схемы автомата исчезнет дешифратор Dcу. Формат двоичного слова приведен ниже.

у1	у2	у3	у4	у5	у6	у7	хm		ах=0			ах=1
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15

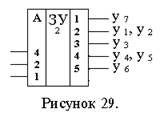
2.            Если общее количество микрокоманд У_i достаточно велико и использование приема, описанного в п1, приведет к значительному увеличению длины операционной части двоичного слова, то можно поступить следующим образом: закодировать пересекающиеся наборы микрокоманд минимальным образом (например, как в предыдущих примерах), в операционной части двоичного слова записать коды этих наборов, а в схеме автомата вместо DСу использовать дополнительное ЗУ. Разрядность адреса этого ЗУ равна разрядности кодов наборов микрокоманд, разрядность слов, записанных в ЗУ, равна количеству У_i в автомате. Каждый разряд слова в этом ЗУ соответствует определенному У_iи в него записывается «0» или «1» в зависимости от значения соответствующего У_iв данном наборе микрокоманд. Например, если использовать данный прием для предыдущего примера, то дополнительное ЗУ должно иметь разрядность адреса равное 3, разрядность слов – 5. Вид такого ЗУ приведен на рис.29.  

Если использовать кодирование наборов микрокоманд такое же, как в предыдущих примерах, то таблица программирования этого ЗУ будет иметь вид:

у7

у1,у2

у3

у4,у5

у6

А\бит	1	2	3	4	5
0	1	0	0	0	0
1	0	1	0	0	0
2	0	0	1	0	0
3	0	0	0	1	0
4	0	0	0	0	1

Адресация микрокоманд в автомате

В автоматах с программируемой логикой используются, в основном, два метода адресации микрокоманд: принудительная и естественная.

При принудительной адресации адрес перехода к следующему двоичному слову в явном (или неявном) виде присутствует в самой микрокоманде. Так, в рассмотренных выше примерах, адресация была принудительная. В двоичном слове для хранения адресов переходов отводилось два поля (при одном логическом условии в слове). Такая микрокоманда называется двухадресной.

Естественная адресация предполагает наличие двоичных слов разного вида, например, операционные и управляющие слова. Операционные слова соответствуют операторным вершинам ГСА управляющего автомата, а управляющие – условным. Если в ГСА автомата есть линейные части (не содержащие условных вершин), то адреса слов, описывающих следующие друг за другом операторные вершины ГСА, должны формироваться в естественном нарастающем порядке: а _t+1 = а _t+ 1,

где: а _t – адрес текущего слова,

     а _t+1 – адрес следующего слова.

Управляющее слово может быть эквивалентно управляющей конструкции некоторого языка программирования:

IF  X _i = 1 THEN GOTO  а_хi=1;

если значение логического условия X _i = 1, то адрес следующего слова а _t+1 = а_хi=1; если  X _i = 0, то адрес следующего слова: а _t+1 = а _t+ 1.   

Естественная адресация микрокоманд в автомате

Формат микрокоманд (двоичных слов) при естественной адресации может быть следующим. Операционная микрокоманда содержит два поля: поле признака вида микрокоманды Р (операционная или управляющая; пусть для операционной – Р=0) и поле, в котором любым из возможных способов записаны значения у_i, которые должен вырабатывать автомат. Управляющая микрокоманда содержит три поля: поле признака Р (пусть для управляющей – Р=1), поле логического условия (может содержать № логического условия X _i ) и поле адреса перехода при X _i = 1.

0

Уi

Формат операционного слова:                        

1

X i

Адр ахi=1.

Формат управляющего слова:

Поскольку для хранения и операционных и управляющих слов используется одно и то же ЗУ, разрядность слов должна быть одинаковой.

Возьмем, для примера, ГСА управляющего автомата, приведенную на рис.5 и запишем алгоритм работы автомата, используя следующие конструкции:

Оператор присваивания вида: у_i = 1, для описания операторных вершин ГСА;

Оператор условного перехода вида: IF  X _i = 1 THEN GOTO  а_хi=1, для описания условных вершин ГСА.

Алгоритм, представленный в виде таблицы, напоминает программу на языке BASIC. Для более эффективного представления, в строках с адресами 1 и 3 перед логическими условиями X₃ и X₁ поставлен знак инверсии (Ø), что позволяет сократить количество строк в записи алгоритма. В строке 8 использована конструкция: GOTO  3 – безусловный  переход к строке 3. Для реализации безусловного перехода введем дополнительное логическое условие, например X₀, а в схеме автомата предусмотрим, что бы всегда X₀= 1. В этом случае, конструкцию  «GOTO  3 » можно заменить на конструкцию:   IF  X₀ = 1 THEN GOTO  3.

Адрес	Оператор
0	У 7 := 1;
1	IF  ØX3 = 1 THEN GOTO  0;
2	У 1 := 1; У 2 := 1;
3	IF  ØX1 = 1 THEN GOTO  5;
4	У 3 := 1;
5	У 4 := 1; У 5 := 1;
6	IF  X 2 = 1 THEN GOTO  0;
7	У 6 := 1;
8	GOTO  3;   (IF  X0 = 1 THEN GOTO  3;)

Из таблицы видно, что закодированная микропрограмма должна содержать 9 строк с адресами в ЗУ от 0 до 8. Поэтому адресное поле управляющей микрокоманды (в которое будем записывать адрес перехода - А) должно содержать не менее четырех разрядов (возьмем ровно 4), а поле логического условия (в которое будем записывать номер логического условия - Нх) должно содержать не менее двух разрядов (так как в нашем примере – 4 различных логических условия). В таблице показано соответствие разрядов двоичного слова и информации, которую содержит слово:

Разряды слова	1	2	3	4	5	6	7
Значения	1	Нх1	Нх0	А3	А2	А1	А0

В первом разряде всегда записывается 1 – признак управляющего слова. В разрядах 2 и 3 записывается номер логического условия Нх в виде двоичного числа: Нх₁ Нх₀, где индексы 0 и 1 – указывают младший и старший разряды числа  Нх. В разрядах 4, 5, 6 и 7 записывается адрес перехода А в виде двоичного числа А₃ А₂ А₁ А₀, где индексы при А так же указывают старшинство разрядов в числе А.

Формат операционного слова выберем следующий:

Разряды слова	1	2	3	4	5	6	7
Значения	0	у7	у1,у2	у3	у4,у5	у6	-

В первом разряде всегда записывается 0 – признак операционного слова. В остальных разрядах будем записывать 1 или 0, в зависимости от того, какое значение имеют микрокоманды у_i в данном слове. В следующей таблице, в колонках, обозначенных номерами разрядов двоичного слова от 1 до 7, приведена закодированная микропрограмма управляющего автомата с естественной адресацией.

Адрес	Оператор	Разряды слова
		1	2	3	4	5	6	7
0	У 7 := 1;	0	1	0	0	0	0	0
1	IF  ØX3 = 1 THEN GOTO  0;	1	1	1	0	0	0	0
2	У 1 := 1; У 2 := 1;	0	0	1	0	0	0	0
3	IF  ØX1 = 1 THEN GOTO  5;	1	0	1	0	1	0	1
4	У 3 := 1;	0	0	0	1	0	0	0
5	У 4 := 1; У 5 := 1;	0	0	0	0	1	0	0
6	IF  X 2 = 1 THEN GOTO  0;	1	1	0	0	0	0	0
7	У 6 := 1;	0	0	0	0	0	1	0
8	IF  X0 = 1 THEN GOTO  3;	1	0	0	0	0	1	1

Для большей наглядности серым фоном в таблице выделены 1-ый разряд – признак вида микрокоманды, и разряды 4..7 – адрес перехода в управляющей микрокоманде. Объем памяти ЗУ – 63 бита.

Схема, обеспечивающая работу с закодированной микропрограммой автомата с естественной адресацией , должна содержать следующие функциональные узлы:

-          память для хранения микропрограммы (ЗУ) объемом не менее девяти слов; чтение слова из памяти осуществляется по адресу (четырехразрядному), подаваемому на адресный вход ЗУ; разрядность слов – 7 бит;

-          схему, обрабатывающую операционную микрокоманду - преобразующую двоичный код в разрядах слова с 2-го по 6-ой в сигналы  у_i на выходе автомата. Эта схема может быть реализована пятью элементами «И»;

-          мультиплексор (MSх), выбирающий из множества входных сигналов Х всего один, номер которого записан в разрядах 2 и 3 управляющего слова; мультиплексор должен иметь дополнительный вход разрешения  V; при  V=1 – режим нормальной работы MSх; при V=0 – режим запрета: на выходе MSх значение «0» независимо от сигналов на его входах;

-          четырехразрядный двоичный счетчик (СТ), имеющий два режима работы: параллельная загрузка адреса перехода (из разрядов 4..7 управляющего слова) в счетчик (когда выполняется условие X_i=1) и режим счета: СТ:=СТ+1 - во всех остальных случаях. Для этого счетчик СТ имеет вход управления V; при  V=0 – режим счета, при  V=1 – режим параллельной загрузки. У счетчика СТ должен быть еще один вход R для установки его в начальное состояние СТ:=0 (Reset).

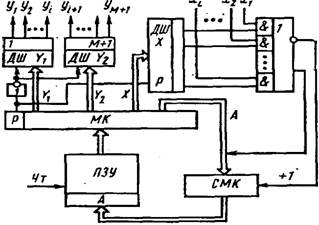
Функциональная схема автомата с программируемой логикой и естественной адресацией приведена на рис.30.

Автомат (рис.30) работает следующим образом. Сигнал Reset=1 устанавливает значение «0» во всех разрядах двоичного счетчика СТ. Код (или двоичное число) А=0000 с выхода СТ подается на адресный вход ЗУ. На выходах ЗУ (разряды 1..7) появляется слово, записанное по адресу А=0 (см. таблицу). В нашем примере по адресу А=0 записана операционная микрокоманда, в которой:

первый разряд имеет значение 0 (признак операционной микрокоманды), поэтому на выходе мультиплексора MSх так же значение 0, а счетчик СТ находится в режиме счета; проинвертированное значение первого разряда (1) подается на входы элементов «И», выполняющих функцию электронных ключей, и на выходах этих элементов – значения 2..7 разрядов микрокоманды, т.е. – значения у_i ; в нашем примере - У₇ ;

так как счетчик в режиме счета (V=0), то при поступлении на вход С счетчика СТ импульса синхронизации, его состояние изменится: СТ:=СТ+1, а значит изменится на +1 адрес: А=0001;  этот адрес поступит на адресный вход ЗУ, на выходе которого появится слово, записанное по данному адресу;

в нашем примере слово по адресу А=0001 – управляющая микрокоманда; первый разряд в этом слове имеет значение 1 (признак управляющей микрокоманды); проинвертированное значение первого разряда (0) подается на входы элементов «И», и на выходах всех этих элементов – значения «0» (все у_i=0); на разрешающий вход мультиплексора MSх подается значение «1»: MSх находится в режиме нормальной работы;

значения разрядов 2 и 3 – подаются на управляющие входы мультиплексора MSх; в нашем примере в этих разрядах записано  двоичное число 11 (3); значение логического условия ØX₃ появляется на выходе MSх;

если ØX₃ = 1 (X₃ = 0), то на вход V счетчика СТ подается «1» (режим параллельной загрузки счетчика) и, при подаче на его вход С импульса синхронизации, в СТ запишутся значения разрядов 4..7  микрокоманды (в нашем примере – это адрес 0000); из ЗУ будет считано слово по этому адресу;

если ØX₃ = 0 (X₃ = 1), то на вход V счетчика СТ подается «0» (режим счета) и, при подаче на его вход С импульса синхронизации, состояние СТ изменится: СТ:=СТ+1; в нашем примере СТ:= 0001+1=0010; запишутся значения разрядов 4..7  микрокоманды (в нашем примере – это адрес 0000); из ЗУ будет считано слово по адресу 0010 (2); и т.д.

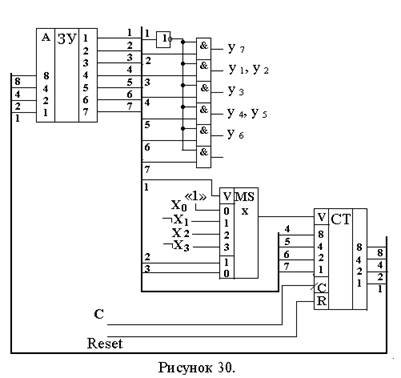
Принудительная адресация микрокоманд в автомате.

В начале раздела на рис.27 и 28 приведены схемы автомата с принудительной адресацией. В отличие от естественной, принудительная адресация сводится к указанию в каждом слове адреса (или адресов) следующего слова. Однако даже при двухадресной микрокоманде, когда в каждом двоичном слове всего одно логическое условие, длина адресной части может быть значительной. Есть различные способы уменьшения длины адресной части в двоичном слове. Один из них заключается в следующем. В адресной части слова записывают адрес перехода при X_i = 0 (Адр _хi=0), а если X _i= 1, то адрес перехода Адр  вычисляется так:

Адр = Адр_хi=0 + 1.

Если использовать логическое значение переменной X_i как арифметическое (0 или 1), то адрес перехода можно вычислить так:

Адр = Адр_хi=0 + X_i.

Таким образом, сократив вдвое длину адресной части двоичного слова, мы не потеряли возможность осуществлять условный переход в автомате с естественной адресацией. Однако при этом получили некоторое неудобство: двоичные слова, к которым происходит переход, всегда находятся в ЗУ в соседних ячейках, так как адреса у них различаются всегда на 1. Поэтому в микропрограмме автомата с описанным способом адресации может появиться избыточность в виде дублирования некоторых слов и безусловных переходов.

№	a m	a s	Y as	Xa ma s
1 2	a 0	a 0 a 1	y7  y1, y2	Ø x 3 x 3
3 4	a 1	a 2 a 3	y3  y4, y5	x 1 Ø x 1
5	a 2	a 3	y4, y5	1
6 7	a 3	a 4 a 0	y6  y7	Ø x 2 x 2
8 9	a 4	a 2 a 3	y3  y4, y5	x 1 Ø x 1

Воспользуемся ГСА (рис.5), прямой таблицей переходов автомата Мура из примера в п.3.1. и форматом микрокоманды из первого примера текущего раздела, в котором в адресной части оставим только одно поле а_х=0. 

К(Уi)			хm		ах=0
1	2	3	4	5	6	7	8

Используем кодирование наборов микрокоманд и дополнительное ЗУ (смотри рис. 29). Микропрограмма с комментариями приведена ниже.

У₀ = {у₇};   У₁ = {у₁, у₂ };    У₂ = {у₃};  У₃ = {у₄, у₅};    У₄ = {у₆}; 

 К(У₀) = 000;  К(У₁) = 001;  К(У₂) = 010;  К(У₃) = 011;  К(У₄) = 100.

Для организации безусловного перехода в этом примере введено дополнительное логическое условие  X₀ . В схеме автомата  на вход X₀ подадим значение «0», а значит переход в этом случае будет всегда по адресу а_х=0, записанному в микрокоманде.

Адрес	Комментарий      \   разряды	1	2	3	4	5	6	7	8
0	a 0; IF   X3 = 0 THEN GOTO  0;	0	0	0	1	1	0	0	0
1	a 1; IF ØX1 = 0 THEN GOTO 2;	0	0	1	0	1	0	1	0
2	a 2; IF   X0 =0 THEN GOTO  3;	0	1	0	0	0	0	1	1
3	a 3; IF  X 2 = 0 THEN GOTO  4;	0	1	1	1	0	1	0	0
4	a 4; IF ØX1 = 0 THEN GOTO 2;	1	0	0	0	1	0	1	0
5	a 0; IF   X3 = 0 THEN GOTO  0;	0	0	0	1	1	0	0	0

Из таблицы видно, что на состояние a ₀ пришлось использовать два слова в ЗУ, тем не менее, общий объем ЗУ в нашем примере 48 бит (меньше, чем у двухадресной микрокоманды). 

Функциональная схема автомата приведена на рис.31.

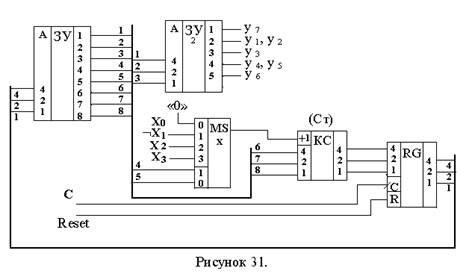
Отличие этой схемы от рис.28 состоит в использовании вместо мультиплексора адреса MSа комбинационного счетчика (Ст). Комбинационная схема (КС), обозначенная как Ст, выполняет функцию: Ст:=А + X_i, где:

Ст – двоичное число на выходе КС;

А – адрес перехода при X_i= 0;

X_i – значение логического условия X_i, выбранного мультиплексором MSх в соответствии с кодом, записанным в разрядах 4 и 5 микрокоманды и интерпретируемым как число 0 или 1.

Функционирование схемы (рис.31) практически не отличается от описанной выше схемы на рис.28.

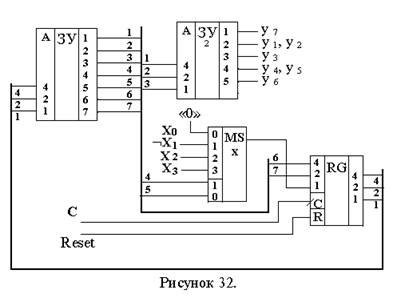
Используя описанный выше прием формирования адресов переходов, можно еще на один разряд сократить адресную часть микрокоманды. Так как адреса переходов всегда отличаются на 1, то в качестве младшего разряда адреса очередной микрокоманды можно использовать значение логического условия X_i. Формат микрокоманды в этом случае имеет вид, приведенный в таблице. Старшие разряды адресной части (а_С) записаны в микрокоманде, а младший разряд формируется из значения логического условия X_i.

К(Уi)			хm		аС		Xi
1	2	3	4	5	6	7	8

В следующей таблице приведена микропрограмма (на основе предыдущего примера), в которой функцию младшего разряда адреса перехода выполняет соответствующее логическое условие X_i, а на рис. 32 – функциональная схема автомата. 

Адрес	Комментарий \ разряды	1	2	3	4	5	6	7	8
0	a 0; IF   X3 = 0 THEN GOTO  0;	0	0	0	1	1	0	0	X3
1	a 1; IF ØX1 = 0 THEN GOTO 2;	0	0	1	0	1	0	1	ØX1
2	a 2; IF   X0 =0 THEN GOTO  6;	0	1	0	0	0	1	1	X0
3	a 3; IF  X 2 = 0 THEN GOTO  4;	0	1	1	1	0	1	0	X 2
4	a 4; IF ØX1 = 0 THEN GOTO 2;	1	0	0	0	1	0	1	ØX1
5	a 0; IF   X3 = 0 THEN GOTO  0;	0	0	0	1	1	0	0	X3
6	a 3; IF  X 2 = 0 THEN GOTO  4;	0	0	0	1	1	0	0	X 2
7

Схема не содержит комбинационного счетчика КС, однако такой формат микрокоманды накладывает на микропрограмму ограничение: при X_i=0 – адрес перехода всегда четный, а при X_i=1 –всегда нечетный.

Таблица для ЗУ 2

А\биты ЗУ2	(у7) 1	(у1,у2) 2	(у3) 3	(у4,у5) 4	(у6) 5
0	1	0	0	0	0
1	0	1	0	0	0
2	0	0	1	0	0
3	0	0	0	1	0
4	0	0	0	0	1

Повышение быстродействия автоматов с принудительной адресацией

Рассмотренные выше схемы и форматы микрокоманд позволяют анализировать в одной микрокоманде только одно логическое условие. Поэтому, если некоторый переход зависит от нескольких логических условий, приходится использовать несколько микрокоманд для описания этого перехода. Таким образом, если логических условий в переходе из состояния a_m  в состояние a_s  два – то требуется два такта работы автомата (две микрокоманды), если три – то три такта и т.д. Очевидно, что быстродействие автомата при этом уменьшается в два, три и более раз.

Понижения быстродействия автомата можно избежать анализируя в одной микрокоманде все логические условия, определяющие переход из состояния a_m  в состояние a_s .

Рассмотрим пример (ГСА_быстрПЛ-.bmp).  

Закодируем группы микрокоманд (К(У_i)) следующим образом:

У₀ = {у₅};          К(У₀) =000;

У₁ = {у₁, у₂ };    К(У₁) =001;

У₂ = {у₃, у₄ };    К(У₂) =010;

У₃ = {у₂, у₃};     К(У₃) =011;

У₄ = {у₄};          К(У₄) =100; 

Закодируем группы логи­ческих условий, опреде­ляющих пере­ходы из со­стояний a_m в состояния a_s. Причем, одинаковые группы будем кодировать оди­наковыми кодами:

Ха₁={х₀},      К(Ха₁) = 01                Ха₂={ х₁,х₂}, К(Ха₂) = 10 

Ха₃={-},        К(Ха₃) = 00

Ха₄={-},        К(Ха₄) = 00

Ха₅={х₃},      К(Ха₅) = 11

По количеству разря­дов микрокоманда бу­дет иметь такой же формат, как и в преды­дущем при­мере, так как разрядность кодов групп микрокоманд (К(У_i)) в нашем примере равна трем (как и в преды­дущем примере), разряд­ность кодов групп логиче­ских условий (К(Ха_i)) равна двум (в предыду­щем примере два разряда использовались для коди­рования логических усло­вий К(Х_i) ). Однако в от­личии от предыду­щего примера, значения раз­рядов в адресной части микро­команды будет зави­сеть от К(Ха_i). Фор­мат микрокоманды приве­ден в таблице.

Обозначим пол­ный адрес в микроко­манде трехразрядным двоичным числом А₂А₁А₀.

К(Уi)			К(Хаi)		Адрес
1	2	3	4	5	6	7	8

Если К(Ха_i)=00 (что соответствует пус­тым группам логических условий Ха₃= {-} и Ха₄={-}), то значения 6, 7 и 8 битов должны зада­ваться явно в микрокоманде числом А₂А₁А₀, что обеспечит безуслов­ный переход по этому адресу.

Если К(Ха_i) = 01 или К(Ха_i) = 11 (что соответствует группам логических условий Ха₁={х₀} и Ха₅={х₃}), то значения 6 и 7 битов задаются в микрокоманде явно (А₂А₁), а значение 8-го бита определяют логические условия х₀ или х₃. Если значение логического условия равно «0», то формируется адрес А₂А₁0, если – «1», то формируется адрес А₂А₁1. Такая микрокоманда обеспечивает условный пере­ход по одному из двух соседних адресов (как в предыдущем примере).

Если К(Ха_i) = 10 (что соответствует группе логических условий Ха₂={ х₁,х₂}), то значение разряда 6 (А₂) задается в микрокоманде явно, а значение 7-го и 8-го битов определяют (соответственно) логиче­ские условия х₁ и х₂. Такая микрокоманда обеспечивает условный пе­реход по одному из четырех соседних адресов:

при  х₁=0 и х₂= 0, формируется адрес А₂00,

при  х₁=0 и х₂= 1, формируется адрес А₂01,

при  х₁=1 и х₂= 0, формируется адрес А₂10,

при  х₁=1 и х₂= 1, формируется адрес А₂11.

Эта микрокоманда определяет переходы по четырем адресам, но на прак­тике некоторые адреса будут приводить к одним и тем же состояниям, что приведет к дублированию некоторых микрокоманд, что увеличи­вает объем используемой памяти ЗУ.

В следующей таблице приведена микропрограмма, в которой используются микрокоманды, описанные выше.

Адрес	Комментарий \ биты м/команды	1	2	3	4	5	6	7	8
0	a1; IF X0 = 0 GOTO 0/1;	0	0	0	0	1	0	0	X0
1	a2; IF К(Ха2)? GOTO 4/5/6/7;	0	0	1	1	0	1	X1	X2
2	a2; IF К(Ха2)? GOTO 4/5/6/7;	0	0	1	1	0	1	X1	X2
3	a1; IF X0 = 0 GOTO 0/1;	0	0	0	0	1	0	0	X0
4	a5; IF X3 = 0  GOTO 2/3;	1	0	0	1	1	0	1	X3
5	a4; GOTO  4;	0	1	1	0	0	1	0	0
6	a3; GOTO  4;	0	1	0	0	0	1	0	0
7	a3; GOTO  4;	0	1	0	0	0	1	0	0

Для реализации схемы формирования адресов в соответствии с приведенными выше микрокомандами используем два мультиплексора.

Эти мультиплексоры в зависимости от кода К(Ха_i) должны сформировать значения разрядов адреса А₁А₀. Значение разряда А₂  всегда (в нашем примере) задается в 6-ом бите микрокоманды.

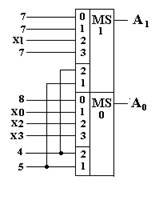
На рисунке приведена схема формиро­вания младших разрядов адреса А₁А₀. На управляющие входы мультиплексоров (2, 1; это не просто цифры, а веса разрядов управляющих входов) подается К(Ха_i) - код группы логических условий (4 и 5 биты микрокоманды). На информационные входы мультиплексоров (0, 1, 2, 3; в зависимости от кода К(Ха_i), представляющего собой двоичное число – номер информационного входа, значение которого появится на выходе MS) подаются значения логических условий (Х_i) и значения 7 и 8 битов микрокоманды.

Логика работы схемы следующая. Если К(Ха_i)=00 (число 0), то на выходах А₁А₀- значения 7 и 8 битов микрокоманды (соответственно). Если К(Ха_i)=01 (число 1), то на выходе А₁ - значение 7 бита, а на выходе  А₀–значение логического условия X₀. Если К(Ха_i)=11 (число 3), то на выходе А₁ - значение 7 бита, а на выходе  А₀–значение логического условия X₃. Если К(Ха_i)=10 (число 2), то на выходе А₁ - значение логического условия X₁, а на выходе  А₀ –значение логического условия X₂.

А\биты ЗУ2	(у1) 1	(у2) 2	(у3) 3	(у4) 4	(у5) 5
0	0	0	0	0	1
1	1	1	0	0	0
2	0	0	1	1	0
3	0	1	1	0	0
4	0	0	0	1	0

Функциональная схема автомата приведена на рисунке.

 (на основе предыдущего примера), в которой функцию младшего разряда адреса перехода выполняет соответствующее логическое условие X_i, а на рис. 32 – функциональная схема автомата. 

Сегментация ЗУ в автоматах с программируемой логикой

Запоминающие устройства, используемые в автоматах с программируемой логикой, имеют достаточно большую емкость, а значит и большую длину адресной части микрокоманды. Большая емкость ЗУ позволяет хранить в нем не одну, а множество микропрограмм, реализующих разные функции, причем каждой из них требуется небольшой объем памяти.

Для того, что бы максимально использовать ЗУ и при этом не увеличивать длину адресной части микрокоманды используют прием, который называется «сегментация ЗУ». Весь объем ЗУ делится на сегменты (страницы), а адрес А, поступающий на адресный вход ЗУ рассматривается как адрес сегмента Ас (обычно старшие разряды адреса) и адрес ячейки в сегменте Ая (обычно младшие разряды адреса). Число сегментов обычно выбирают равным целой степени двойки (2, 4, 8 и т.д. сегментов).

Микропрограммы в ЗУ необходимо размещать так, чтобы было как можно меньше переходов из сегмента в сегмент, а значит лучше всего, что бы первая микрокоманда микропрограммы размещалась в первой ячейке некоторого сегмента. В этом случае в адресной части микрокоманды в качестве адреса перехода будет записываться адрес ячейки Ая и только при   необходимости перехода в другой сегмент микрокоманда должна содержать полный адрес: Ас и Ая.  Полный адрес необходимо так же записать в регистр адреса при выборе той или иной микропрограммы в ЗУ.

Использование сегментации ЗУ в автоматах с принудительной адресацией и одноадресной микрокомандой рассмотрим на примере автомата, описанного ГСА рис.5 с кодированием групп микрокоманд (как в примере на рис.28).

Пусть ЗУ имеет 8-ми разрядный адрес (емкость ЗУ - 256 слов). Представим ЗУ состоящим из 32-х сегментов, в каждом из которых – 8 ячеек. Таким образом, 5 старших разрядов адреса – это адрес сегмента (Ас), а 3 младших – адрес ячейки (Ая).

Формат микрокоманды практически не отличается от используемого в примере рис.31. Для записи признака перехода из одного сегмента в другой в микрокоманду введем дополнительный разряд (0): значение этого разряда «0» - обычная микрокоманда (как в примере рис.31), если «1» - то все остальные 8 разрядов микрокоманды интерпретируются как полный адрес перехода А = Ас Ая.

Пусть адрес первой микрокоманды микропрограммы А=00000011, т.е. Ас=00000, Ая=011. Микропрограмма с комментариями приведена ниже.( 90 бит )

Ас	Ая	Комментарий \ разряды	0	1	2	3	4	5	6	7	8
00000	011	a 0; IF X3 = 0 THEN GOTO 3;	0	0	0	0	1	1	0	1	1
00000	100	a 1; IF ØX1 = 0 THEN GOTO 5;	0	0	0	1	0	1	1	0	1
00000	101	a 2; IF X0 =0 THEN GOTO  6;	0	0	1	0	0	0	1	1	0
00000	110	GOTO-S 1,0;	1	0	0	0	0	1	0	0	0
00000	111		0	0	0	0	0	0	0	0	0
00001	000	a 3; IF X2 = 0 THEN GOTO 1;	0	0	1	1	1	0	0	0	1
00001	001	a 4; IF ØX1 = 0 THEN GOTO 3;	0	1	0	0	0	0	0	1	1
00001	010	GOTO-S 0,3;	1	0	0	0	0	0	0	1	1
00001	011	GOTO-S 0,5;	1	0	0	0	0	0	1	0	1
00001	100	GOTO-S 1,0;	1	0	0	0	0	1	0	0	0

Первые 3 строки (по смыслу) совпадают с примером рис.31. В нулевом разряде записан «0», в адресной части – Ая сегмента с адресом Ас=00000.

Конструкция «GOTO-S Ас, Ая » в комментариях означает переход по полному адресу А = Ас Ая. Следует обратить внимание на то, что в нулевом разряде этой микрокоманды - «0», а в операционной части – Ас (а не У_i ).

По аналогии с примером (рис.31), в 4-ой строке следовало бы записать конструкцию: «a _3; IF  X ₂ = 0 THEN GOTO  7», однако Ая = 7 – это адрес последней ячейки сегмента с адресом Ас=0, и при X ₂ = 1 адрес Ая = 7 + X ₂ = 8. Поскольку под Ая отведено 3 разряда, то после этой операции получим  Ая=0. Поэтому в 4-ой строке «GOTO-S 1,0» - переход в сегмент с Ас=00001 в ячейку с Ая=000. 5-ая строка при этом не используется.

В 6-ой строке конструкция «a ₃; IF X₂ = 0 THEN GOTO 1;»  по смыслу совпадает с конструкцией «a _3; IF  X ₂ = 0 THEN GOTO  4;» (рис.31), причем «GOTO-S0,3;» в 8-ой строке – переход в начало микропрограммы (где  «a ₀; IF X₃ = 0 THEN GOTO 3;» эквивалентно «a ₀; IF   X₃ = 0 THEN GOTO  0;»(рис.31).

В 7-ой строке «a ₄; IF ØX₁ = 0 THEN GOTO 3;» и далее «GOTO-S0,5;» и «GOTO-S 1,0;» эквивалентно одной строке из примера рис.31 «a ₄; IF  ØX₁ = 0 THEN GOTO  2;»

На рис.33 приведена функциональная схема автомата с принудительной адресацией и сегментацией ЗУ. Для упрощения в ней не показаны элементы, обеспечивающие запись в регистр адреса начального адреса микропрограммы.

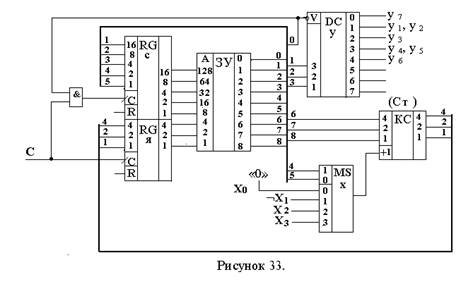
Регистр адреса состоит из двух независимых регистров:RGс – регистр адреса сегмента и RGя – регистр адреса ячейки. Пока значение нулевого разряда слова равно «0» - разрешается работа дешифратора DСy  и разряды слова 1..3 интерпретируются как код группы микрокоманд У_i. В RGя при каждом синхроимпульсе записывается Ая, формируемый КС (как в примере рис.31). Если значение нулевого разряда слова «1», то работа DСy запрещается (на всех выходах DСy – «0»), а импульс синхронизации через элемент «И» подается не только на вход С RGя , но и RGс. Происходит запись полного адреса перехода в оба регистра: А=Ас Ая.

В остальном работа схемы не отличается от схемы на рис.31.