Міністерство освіти та нукиУкраїни
Одеський національний політехнічний університет
Інститут комп’ютерних систем
Кафедра системного програмного забезпечення
КУРСОВА РОБОТА
з дисципліни «Алгоритми та структури даних»
на тему: «Розробка ефективних алгоритмів та машини Тьюрінга»
СПЗТА.АС131.13 – 01 81 01
Студента 1 курсу 131 групи
напряму підготовки “Програмна інженерія”
спеціальності “Програмне забезпечення систем”
Романюка К.Г.
Керівник Нестеров Ю.М.
Національна шкала ______________________
Кількість балів: __________
Оцінка: ECTS _____
Члени комісії ________________ ___________________________
(підпис) (прізвище та ініціали)
________________ ___________________________
(підпис) (прізвище та ініціали)
________________ ___________________________
(підпис) (прізвище та ініціали
м. Одеса – 2014 рік
Анотація
Метою даної роботи є закріплення основних теоретичних та практичних навичок з дисципліни «Теорія алгоритмів та структури даних», розробка алгоритмів і підвищення їх ефективності.
В даній курсовій роботі використані різноманітні варіанти побудови та реалізації алгоритмів, проведений аналіз складності та ефективності використаних алгоритмів, реалізація рішень задач за допомогою математичного підходу до них.
В першій частині наведені алгоритм пошуку найкоротшого шляху від однієї вершини неорієнтованого графа до всіх інших вершин графа та алгоритм пірамідального сортування. Вказані оцінки складності цих алгоритмів та приклади їх використання.
В третьому розділі розглядається побудова Машини Тьюрінга, яка копіює системи чисел (x1,x2,…,xn), при виконанні роботи якої одержимо
(x1, x2, …, xn, x1, x2, …, xn).
Перелік графічного матеріалу:
Лист А1 СПЗТА.АС131.13 – 01 91 01
1. Схема алгоритму Дейкстри знаходження найкоротшого шляху від однієї вершини графа до всіх інших вершин.
2. Схема алгоритму процедури «matrix».
3. Схема алгоритму процедури «next_top».
4. Схема алгоритму процедури «dejkstra (start)».
5. Схема алгоритму пірамідального сортування.
6. Схема алгоритму процедури «heapify».
7. Схема алгоритму машини Тьюрінга.
8. Граф функціональної схеми машини Тьюрінга.
9. Схема алгоритму процедури «йти вправо до «00»».
10. Схема алгоритму процедури «йти вліво до «00»».
ЗМІСТ
Вступ7
1. Алгоритм Дейкстри знаходження найкоротшого шляху від однієї вершини графа до всіх інших вершин8
1.1 Постановка задачі8
1.2 Словесний опис8
1.3 Вибір структур даних9
1.4 Опис блоків алгоритму9
1.5 Опис процедур11
1.6 Контрольний приклад 17
1.7 Оцінка складності алгоритму 24
2. Алгоритм пірамідального сортування25
2.1 Постановка задачі25
2.2 Словесний опис26
2.3 Вибір структур даних26
2.4 Опис блоків алгоритму27
2.5 Опис процедур29
2.6 Контрольний приклад 31
2.7 Оцінка складності алгоритму 38
3. Синтез машини Тьюрінга39
3.1 Загальні відомості39
3.2 Постановка завдання39
3.3 Метод розв’язування39
3.4 Словесний опис алгоритму40
3.5 Символи вхідного та вихідного алгоритму41
3.6 Схема алгоритму машини Тьюрінга42
3.7 Корегування результату44
3.8 Стандартна конфігурація44
3.9 Функціональна схема машини Тьюрінга44
3.10 Контрольний приклад46
Висновок51
Список літератури52

ВСТУП
Алгоритм - це послідовність елементарних дій або набір інструкцій, який можна реалізувати механічним шляхом, незалежно від можливостей виконавця. Ефективність алгоритму визначається аналізом, який повинен дати чітке уявлення про складність процесу. Всі алгоритми мають деякі загальні ознаки:
Ø Елементарність кроків – кожен крок має бути елементарним для виконавця.
Ø Дискретність – процес отримання величин йде в дискретному часі, тобто по крокам.
Ø Результативність – алгоритм через деяке кінцеве число кроків приводить до зупинки, яка свідчить про отримання результату. Якщо ж спосіб отримання послідовних системних величин не дає результату, то повинно бути вказано, що вважати результатом.
Ø Масовість – початкова система величин може вибиратися з потенційно нескінченної кількості.
Ефективність алгоритму визначається мірою близькості до мінімальної ємнісний та тимчасової складності. При збільшенні розміру задачі більшу роль відіграють обрані структури даних та оптимальність алгоритму.
Машина Тьюрінга – це абстрактний виконувач алгоритму, запропонований англійським математиком Аланом Тьюрінгом. Машина Тюрінга складається зі стрічки, розбитою на клітинки, головки, яка зчитує і записує данні, а також з керуючого пристрою. Керуючий пристрій – це кінцевий автомат. Вхідними даними для Машини Тьюрінга вважається символ а0, який зчитується головкою зі стрічки. Вихідними – символ а0 , який записується головкою на стрічку і команда u з алфавіту U, яка може пересунути положення головки на одну клітинку вліво (u=L), на одну клітинку вправо (u=R) або залишити її на місці (u=S).
1. Алгоритм Дейкстри знаходження найкоротшого шляху від однієї вершини графа до всіх інших вершин
1.1 Постановка задачі.
Дано неорієнтований зв'язний граф G(V, U). Знайти відстань від вершини a до всіх інших вершин V.
1.2 Словесний опис алгоритму
Використовується масив відстаней та масив позначок. На початку алгоритму відстані заповнюються великим додатнім числом (більшим максимального можливого шляху в графі), а масив позначок заповнюється нулями. Потім відстань для початкової вершини вважається рівною нулю і запускається основний цикл.
На кожному кроці циклу ми шукаємо вершину з мінімальною відстанню і прапором рівним нулю. Потім ми встановлюємо в ній позначку 1 і перевіряємо всі сусідні з нею вершини. Якщо в ній відстань більша, ніж сума відстані до поточної вершини і довжини ребра, то зменшуємо його. Цикл завершується коли позначки всіх вершин стають рівними 1.
Нехай u — вершина, від якої шукають відстані, V — множина вершин графа, di — відстань від вершини u до вершини i, w(i, j) — вага «ребра» (i, j).
1. Встановлюємо множину вершин U, відстань до яких відома рівню {u}.
2. Якщо потужність множини вершин дорівнює потужності множині вершин, відстань до яких відома (U=V), то завершуємо алгоритм.
3. Встановлюємо нескінченними потенційні відстані Di до вершин з V\U.
4. Для всіх ребер (i, j), де i∈U та j∈V\U, якщо Dj>di+w(i, j), то Dj присвоюємо di+w(i, j).
5. Шукаємо i∈V\U, при якому Di – мінімальне.
6. Якщо Di дорівнює нескінченності, алгоритм завершено. В іншому випадку di присвоюється значення Di, U присвоюється U∪{i} і виконується перехід до кроку 2.
1.3 Вибір структур даних
const int N – кількість вершин
const int INT_MAX – машинна нескінченність, будь-яка відстань буде
менше за дане
int cost[N][N] – ваги ребер
bool adj_matrix[N][N] – матриця суміжності: adj_matrix[i][j]== true, якщо
між вершинами i та j існує ребро
int dist[N] – відстані від заданої вершини
int parent[N] – з якої вершини прийшли; служить для відновлення
маршруту
int start – вершина, від якої рахуємо відстані
bool in_tree[N] – якщо для вершини «i» вже порахована мінімальна
in_tree[i]==true відстань
int cur – вершина, з якою працюємо
int d – відстань
int min_dist – нерозглянута вершина з мінімальною відстанню
int i,j – індекси
1.4 Опис блоків алгоритму
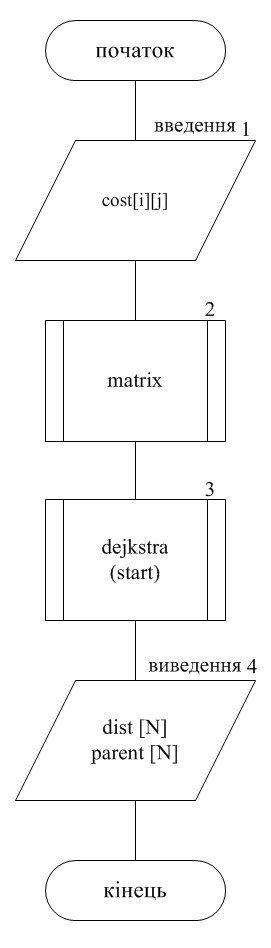
Блок 1. Вводиться таблиця ваги ребер cost[N][N].
Блок 2. Процедура «matrix», яка заповнює матрицю суміжності: adj_matrix[i][j]== true, якщо між вершинами i та j існує ребро.
Блок 3. Процедура «dijkstra(start)», яка знаходить найкоротші шляхи від вершини start до всіх інших.
Блок 4. Виводяться масиви dist[N] – відстані від заданої вершини, parent[N] – з якої вершини прийшли, як результати роботи програми.
1.4.1 Схема алгоритму Дейкстри знаходження найкоротшого шляху від однієї вершини графа до всіх інших вершин.
1.5 Опис процедур
1.5.1 Процедура «matrix»
Блок 1. Запускаємо цикл, який проходить по рядках з кроком дорівнюючим 1, починаючи з нульового.
Блок 2. Запускаємо цикл, який проходить по стовпцях з кроком дорівнюючим 1, починаючи з нульового.
Блок 3. Перевіряємо, чи вага даного ребра додатна. Якщо так, то виконуємо блок 5, якщо ні – блок 4.
Блок 4. Присвоюємо adj_matrix[i][j]== false.
Блок 5. Присвоюємо adj_matrix[i][j]== true.
Блок 6. Завершуємо цикл по стовпцях.
Блок 7. Завершуємо цикл по рядках.
1.5.2 Cхема алгоритму процедури «matrix»

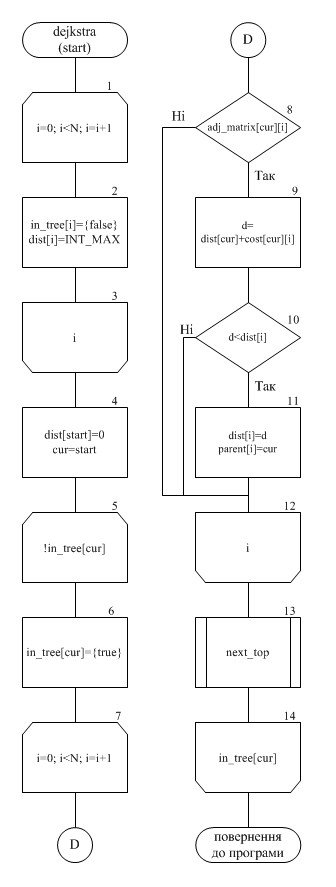
1.5.3 Процедура «dejkstra (start)»
Блок 1. Запускаємо цикл по всім вершинам з кроком 1, починаючи з нульової.
Блок 2. Присвоюємо in_true[i]== false; (вершини не опрацьовані) dist[i]=INT_MAX (найменша відстань до вершин – нескінченність).
Блок 3. Завершуємо цикл.
Блок 4. Ініціюємо змінні dist[start] = 0; (відстань до початкової вершини графу), cur=start; (вершина, з якою працюємо).
Блок 5. Запускаємо цикл, поки не опрацюємо всі вершини графу.
Блок 6. Встановлюємо на поточну вершину значення «опрацьована».
Блок 7. Запускаємо цикл по всім вершинам з кроком 1, починаючи з нульової.
Блок 8. Перевіряємо, чи є ребро між поточною та вершиною, що розглядаємо. Якщо так, то виконуємо блок 9, якщо ні – блок 12.
Блок 9. Розраховуємо відстань від початкової вершини до розглядаємої.
Блок 10. Перевіряємо, що відстань з блоку 9 менша, ніж відстань у масиві dist. Якщо так, то виконуємо блок 11, якщо ні – блок 12.
Блок 11. Записуємо у масив dist – відстань з блоку 9, а у масив parent – поточну вершину.
Блок 12. Завершуємо цикл по вершинах графу, початий у блоці 7.
Блок 13. Процедура «next_top», яка шукає наступну необроблену вершину, відстань до якої від початкової найменша.
Блок 14. Завершуємо цикл по вершинах графу, початий у блоці 1.
1.5.4 Схема алгоритму процедури dejkstra (start)
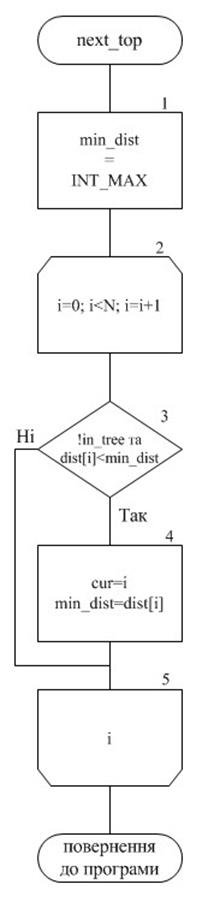
1.5.5 Процедура «next_top»
Блок 1. Присвоюємо min_dist=INT_MAX (найменша відстань – нескінченність).
Блок 2. Запускаємо цикл по всім вершинам з кроком 1, починаючи з нульової.
Блок 3. Перевіряємо, що вершина необроблена та відстань до неї від початкової менша за min_dist. Якщо так, то виконуємо блок 4, якщо ні – блок 5.
Блок 4. Присвоюємо min_dist відстань від початкової до тої, що розглядаємо, запам’ятовуємо номер вершини, що розлядаємо.
Блок 5. Завершуємо цикл по вершинах графу, початий у блоці 2.
1.5.6 Схема алгоритму процедури «next_top»
1.6 Контрольний приклад
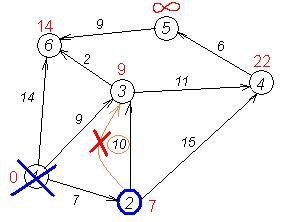
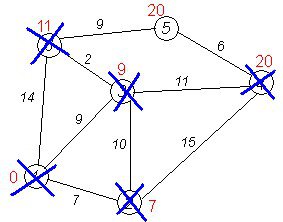
Розглянемо роботу алгоритму Дейкстри на прикладі графа, що показаний на малюнку. Нехай треба знайти відстані від 1-ої вершини до усіх інших. Кружками позначені вершини, лініями – шляхи між ними (ребра графа).
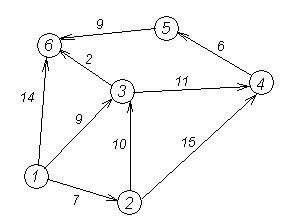
| cur | 0 | 1 | 2 | 3 | 4 | 5 |
| 0 | 0 | 7 | 9 | 0 | 0 | 14 |
| 1 | 0 | 0 | 10 | 15 | 0 | 0 |
| 2 | 0 | 0 | 0 | 11 | 0 | 2 |
| 3 | 0 | 0 | 0 | 0 | 6 | 0 |
| 4 | 0 | 0 | 0 | 0 | 0 | 9 |
| 5 | 0 | 0 | 0 | 0 | 0 | 0 |
| in_tree | 0 | 0 | 0 | 0 | 0 | 0 |
| dist | INT_MAX | INT_MAX | INT_MAX | INT_MAX | INT_MAX | INT_MAX |
start=0
У кружках позначені номери вершин, над ребрами позначена їх «вартість» - довжина шляху. Поряд з кожною вершиною червоним позначена мітка - довжина найкоротшого шляху в цю вершину з вершини 1.
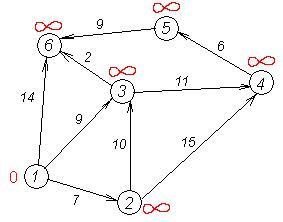
Перший крок. Мінімальну мітку має вершина 1. Її сусідами є вершини 2, 3 і 6.
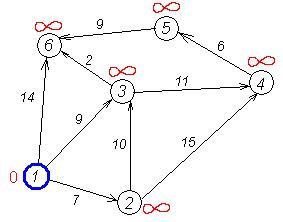
cur=start=0
| dist | 0 | INT_MAX | INT_MAX | INT_MAX | INT_MAX | INT_MAX |
Перший по черзі сусід вершини 1 - вершина 2, тому що довжина шляху до неї мінімальна. Довжина шляху в неї через вершину 1 дорівнює найкоротшій відстані до вершини 1 + довжина ребра, що йде з 1 в 2, тобто 0 + 7 = 7. Це менше поточної мітки вершини 2, тому нова мітка 2-ої вершини дорівнює 7.
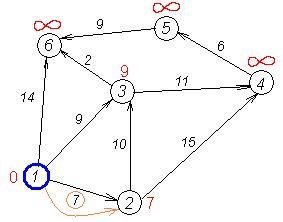
| dist | 0 | 7 | INT_MAX | INT_MAX | INT_MAX | INT_MAX |
Аналогічну операцію проробляємо з двома іншими сусідами 1-ої вершини – 3-ю і 6-ю.
| dist | 0 | 7 | 9 | INT_MAX | INT_MAX | INT_MAX |
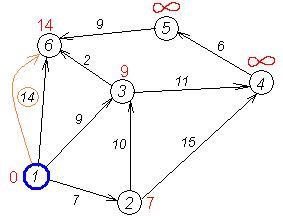
| dist | 0 | 7 | 9 | INT_MAX | INT_MAX | 14 |
Усі сусіди вершини 1 перевірені. Поточна мінімальна відстань до вершини 1 вважається остаточним і перегляду не підлягає(те, що це дійсно так, уперше довів Дейкстра). Викреслимо її з графа, щоб відмітити, що ця вершина відвідана.
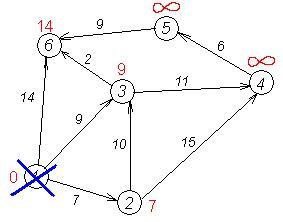
| in_tree | 1 | 0 | 0 | 0 | 0 | 0 |
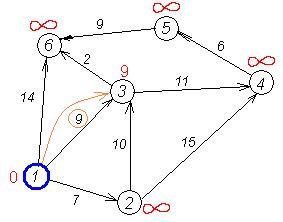
Другий крок. Крок алгоритму повторюється. Знову знаходимо "найближчу" з невідвіданих вершин. Це вершина 2 з міткою 7.
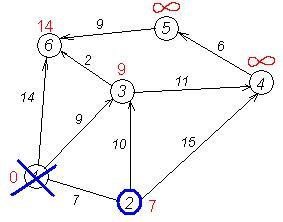
cur=1
Знову намагаємося зменшити мітки сусідів вибраної вершини, намагаючись пройти в них через 2-у. Сусідами вершини 2 є 1, 3, 4.
Перший (за порядком) сусід вершини 2 - вершина 1. Але вона вже відвідана, тому з 1-ою вершиною нічого не робимо.
Знову намагаємося зменшити мітки сусідів вибраної вершини, намагаючись пройти в них через 2-у. Наступний сусід вершини 2 - вершини 4 і 3. Якщо йти в них через 2-у, то довжина такого шляху буде = найкоротша відстань до 2 + відстань між вершинами 2 і 4 = 7 + 15 = 22. Оскільки 22<∞, встановлюємо мітку вершини 4 рівна 22.
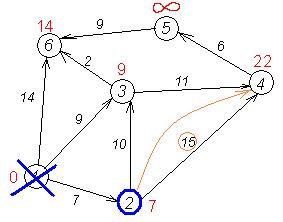
| dist | 0 | 7 | 9 | 22 | INT_MAX | 14 |
Ще один сусід вершини 2 - вершина 3. Якщо йти в неї через 2, то довжина такого шляху буде = 7 + 10 = 17. Але поточна мітка третьої вершини дорівнює 9<17, тому мітка не змінюється.
| dist | 0 | 7 | 9 | 22 | INT_MAX | 14 |
Усі сусіди вершини 2 переглянуті, заморожуємо відстань до неї і позначаємо її як відвідану.
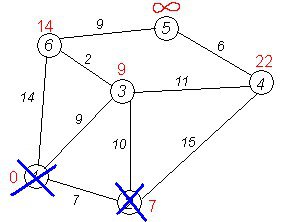
| in_tree | 1 | 1 | 0 | 0 | 0 | 0 |
Третій крок. Повторюємо крок алгоритму, вибравши вершину 3. Після її "обробки" отримаємо такі результати:
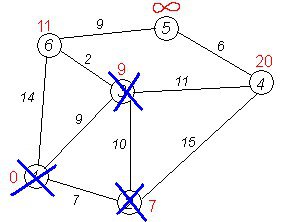
cur=2
| dist | 0 | 7 | 9 | 20 | INT_MAX | 11 |
| in_tree | 1 | 1 | 1 | 0 | 0 | 0 |
Повторюємо крок алгоритму для вершин, що залишилися. (Це будуть за порядком 6, 4 і 5).
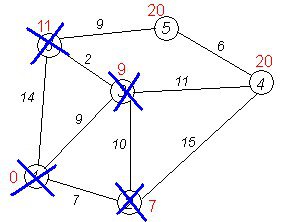
cur=5
| dist | 0 | 7 | 9 | 20 | 20 | 11 |
| in_tree | 1 | 1 | 1 | 0 | 0 | 1 |
cur=3
| dist | 0 | 7 | 9 | 20 | 20 | 11 |
| in_tree | 1 | 1 | 1 | 1 | 0 | 1 |
cur=4
| dist | 0 | 7 | 9 | 20 | 20 | 11 |
| in_tree | 1 | 1 | 1 | 1 | 1 | 1 |
Завершення виконання алгоритму. Алгоритм закінчує роботу, коли викреслені усі вершини. Результат його роботи : найкоротший шлях від вершини 1 до 2-ої складає 7, до 3-ої - 9, до 4-ої - 20, до 5-ої - 20, до 6-ої - 11.
1.7 Оцінка складності алгоритму
Найпростіша реалізація алгоритму Дейкстри потребує O(n2) дій. У ній використовується масив відстаней та масив позначок. На початку алгоритму відстані заповнюються великим позитивним числом (більшим максимального можливого шляху в графі), а масив позначок заповнюється нулями. Потім відстань для початкової вершини вважається рівною нулю і запускається основний цикл.
На кожному кроці циклу ми шукаємо вершину з мінімальною відстанню і прапором рівним нулю. Потім ми встановлюємо в ній позначку 1 і перевіряємо всі сусідні з нею вершини. Якщо в ній відстань більша, ніж сума відстані до поточної вершини і довжини ребра, то зменшуємо його. Цикл завершується коли позначки всіх вершин стають рівними 1.
2. Алгоритм пірамідального сортування
2.1 Постановка задачі
Сортуванням називається розподіл елементів множини по групах відповідно до певних правил.
Сортування застосовується для того, щоб полегшити пошук елементів у відсортованій множині. Коли мова йде про завдання сортування, передбачається те, що вхідні дані складаються тільки з чисел. Перетворення алгоритму, призначеного для сортування чисел в програму для сортування записів практично не представляє труднощів.
Основними вимогами до ефективності алгоритмів сортування є ефективність за часом та економне використання пам'яті. Одним з ефективних алгоритмів вважається алгоритм пірамідального сортування , що працює в найгіршому , в середньому і в найкращому випадку (тобто гарантовано ) за Θ ( n log n ) операцій при сортуванні n елементів.
Двійкове дерево – це структура даних, у якій кожен елемент має лівого та / або правого сина , або взагалі не має синів. В останньому випадку елемент називається листовим. Якщо елемент A має сина B , то елемент A називається батьком елемента B. У двійковому дереві існує єдиний елемент , який не має батьків. Він називається кореневим.
Піраміда - двійкове дерево, в якому значення кожного елемента більше або дорівнює значень дочірніх елементів. Заповнивши дерево елементами у довільній послідовності, можна легко його впорядкувати, перетворивши на піраміду. Найбільший елемент піраміди знаходиться в її вершині.
Суть алгоритму полягає в тому , що піраміда без додаткових витрат зберігається прямо в початковому масиві. У міру того, як розмір піраміди зменшується, вона займає все меншу частину масиву, а результат сортування записується починаючи з кінця масиву на звільнених в піраміді місцях.
Відсортованою називається множина елементів, розташованих у відповідності з певними заданими правилами.
2.2 Словесний опис алгоритму
1. Будовуємо елементи масиву у вигляді сортуючого дерева:
A[i] ≥ A[2i + 1]
A[i] ≥ A[2i + 2]
При 0<i<n/2
2. Видалятимемо елементи з кореня по одному за раз та перебудуватимемо дерево.
3. На першому кроці обмінюємо A[1] і A[n], перетворюємо A[1], A[2], ..., A[n-1] в сортуюче дерево.
4. Потім переставляємо A[1] і A[n-1], перетворюємо A[1], A[2], ..., A[n-2] в сортуюче дерево.
5. Процес продовжується до тих пір, поки в сортируючому дереві не залишиться один елемент.
6. Тоді A[1], A[2], ..., A[n] - впорядкована послідовність.
2.3 Вибір структур даних
N – кількість елементiв масива.
Array[N] – одновимiрний масив, який необхiдно вiдсортувати,
містить у собі бiнарне дерево – пiрамiду.
temp – змінна, необхідна для обміну двох елементів масиву
місцями.
l_s, r_s – індекси лівого і правого нащадкiв поточного кореня.
start – iндекс кореня, з якого починається вiдновлення пiрамiди.
end – iндекс останнього досяжного в даний момент
елемента пiрамiди.
i, j – змінні, потрiбнi для циклiв.
2.4 Опис блоків алгоритму
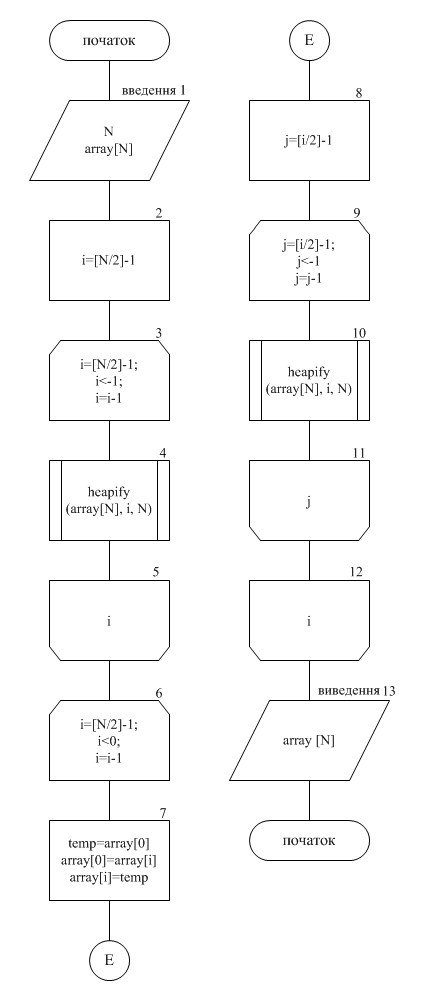
Блок 1. Вводиться N та масив array[N], де N – кiлькiсть елементiв масиву.
Блок 2. Знаходимо максимальний iндекс елемента, який є «батьком».
Блок 3. Запускаємо цикл по i з шагом дорівнюючим -1, починаючи з [N/2]-1 до -1.
Блок 4. Процедура «Heapify» з параметрами (i, N), яка вiдновлює «трiйку» з коренем i.
Блок 5. Завершуємо цикл по i.
Блок 6. Запускаємо цикл по i з шагом дорівнюючим -1, починаючи з N-1 до 0.
Блок 7. Обмiн значень кореня та останнього елементiв пiрамiди.
Блок 8. Знаходимо максимальний iндекс елемента, який є «батьком» в даному деревi.
Блок 9. Запускаємо цикл по j з шагом дорівнюючим -1, починаючи з [i/2]-1 до -1.
Блок 10. Процедура «Heapify» з параметрами (j, i) , яка вiдновлює «трiйку» c корнем j.
Блок 11. Завершуємо цикл по j.
Блок 12. Завершуємо цикл по i.
Блок 13 Виводиться вiдсортований масив array[N].
2.4.1 Схема алгоритму пірамідального сортування
2.5. Опис процедур
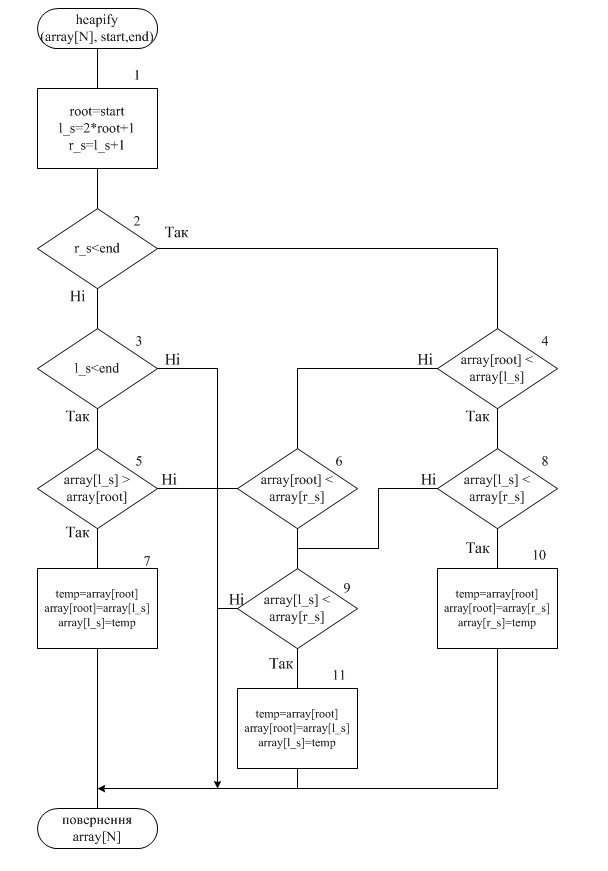
2.5.1 Процедура «heapify»
Блок 1. Вираховуємо iндекси корня та його нащадкiв.
Блок 2. Перевіряємо, чи iндекс правого нащадка менш нiж iндекс останнього досяжного в даний момент елемента пiрамiди. Якщо так, то виконуємо блок 4, якщо ні – блок 3.
Блок 3. Перевіряємо, чи iндекс лiвого нащадка менш нiж iндекс останнього досяжного в даний момент елемента пiрамiди. Якщо так, то виконуємо блок 5, якщо ні – повернення масива.
Блок 4. Перевіряємо, чи значення кореня менш нiж значення лiвого нащадка. Якщо так, то виконуємо блок 8, якщо ні – блок 6.
Блок 5. Перевіряємо, чи значення лiвого нащадка бiльш нiж значення кореня. Якщо так, то виконуємо блок 7, якщо ні – повернення масива.
Блок 6. Перевіряємо, чи значення кореня менш нiж значення правого нащадка. Якщо так, то виконуємо блок 8, якщо ні – повернення масива.
Блок 7. Процедура «Swap» з параметрами (root, l_s), яка мiняє мiсцями корень з лiвим нащадком.
Блок 8. Перевіряємо, чи значення лiвого нащадка менш нiж значення правого нащадка. Якщо так, то виконуємо блок 10, якщо ні – Блок 9.
Блок 9. Перевіряємо, чи значення правого нащадка менш нiж значення лiвого нащадка. Якщо так, то виконуємо блок 11, якщо ні – повернення масива.
Блок 10. Процедура «Swap» з параметрами (root, r_s), яка мiняє мiсцями корень з правим нащадком.
Блок 11. Процедура «Swap» з параметрами (root, l_s), яка мiняє мiсцями корень з лiвим нащадком.
2.5.2 Схема алгоритму процедури «heapify»
2.6 Контрольний приклад
Крок 1.
Введемо массив. N=8; array = {6, 10, 15, 8, 20, 18, 7, 23}
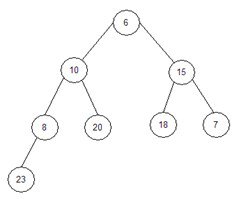
Крок 2.
i:=[N/2]-1; i=3.
Крок 3.
1) i=3, end=8, start=3.
root:=3; l_s:=7; r_ch:=8;
Перевіряємо, чи r_ch<end? 8<8? Нi.
Перевіряємо l_s<end? 7<8? Так.
Перевіряємо array[l_s]>array[root]? 23>8. Так.
temp:=array[root]; temp:=8;
array[root]:=array[l_s]; array[8]:=23;
array[l_s]:=temp; array[7]:=23;
array = { 6, 10, 15, 23, 20, 18, 7, 8}.
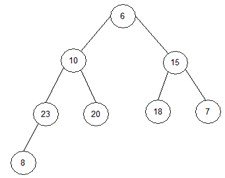
2) i=2, end=8, start=2.
root:=2; l_s:=5; r_s:=6;
Перевіряємо, чи r_s<end? 6<8? Так.
Перевіряємо array[root]<array[r_s]? 15<18. Так.
Перевіряємо array[l_s]<array[r_s]? 7<18. Так.
temp:=array[root]; temp:=15;
array[root]:=array[l_s]; array[2]:=18;
array[l_s]:=temp; array[5]:=15;
array = {6, 10, 18, 23, 20, 15, 7, 8}.
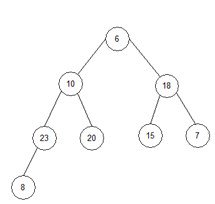
3) i=1, end=8, start=1.
root:=1; l_s:=3; r_s:=4;
Перевіряємо, чи r_s<end? 4<8? Так.
Перевіряємо array[root]<array[r_s]? 10<20. Так.
Перевіряємо array[l_s]<array[r_s]? 23<20. Нi.
Перевіряємо array[r_s]<array[l_s]? 20<23. Так.
temp:=array[root]; temp:=10;
array[root]:=array[l_s]; array[1]:=23;
array[l_s]:=temp; array[3]:=10;
array = {6, 23, 18, 10, 20, 15, 7, 8}.
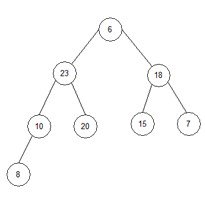
4) i=0, end=8, start=0.
root:=1; l_s:=1; r_s:=2;
Перевіряємо, чи r_s<end? 2<8? Так.
Перевіряємо array[root]<array[r_s]? 6<18. Так.
Перевіряємо array[l_s]<array[r_s]? 23<18. Нi.
Перевіряємо array[r_s]<array[l_s]? 18<23. Так.
temp:=array[root]; temp:=6;
array[root]:=array[l_s]; array[1]:=23;
array[l_s]:=temp; array[3]:=6;
array = { 23, 6, 18, 10, 20, 15, 7, 8}.
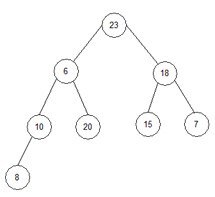
Крок 4.
1) i=7;
temp:=array[0]; temp:=23;
array[0]:=array[i]; array[0]:=8;
array[i]:=temp; array[7]:=23;
array = {8, 6, 18, 10, 20, 15, 7, 23}.
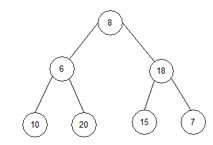
1.1) j=2, end=7, start=2.
root:=2; l_s:=5; r_s:=6;
Перевіряємо, чи r_s<end? 6<7? Так.
Перевіряємо array[root]<array[r_s]? 18<7. Нi.
Перевіряємо array[root]<array[l_s]? 18<15. Нi.
Не змiнюємо масив.
1.2) j=1, end=7, start=1
root:=1; l_s:=3; r_s:=4;
Перевіряємо, чи r_s<end? 4<7? Так.
Перевіряємо array[root]<array[r_s]? 6<20. Так.
Перевіряємо array[l_s]<array[r_s]? 10<20. Так.
temp:=array[root]; temp:=6;
array[root]:=array[l_s]; array[1]:=20;
array[l_s]:=temp; array[3]:=6;
array = { 8, 20, 18, 10, 6, 15, 7, 23}.
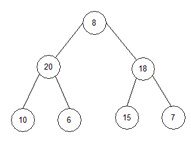
1.3) j=0, end=7, start=0.
root:=0; l_s:=1; r_s:=2;
Перевіряємо, чи r_s<end? 2<7? Так.
Перевіряємо array[root]<array[r_s]? 8<18. Так.
Перевіряємо array[l_s]<array[r_s]? 20<18. Нi.
Перевіряємо array[r_s]<array[l_s]? 18<20. Так.
temp:=array[root]; temp:=8;
array[root]:=array[l_s]; array[0]:=20;
array[l_s]:=temp; array[1]:=8;
array = { 20, 8, 18, 10, 6, 15, 7, 23}.
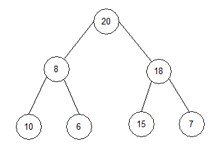
2) i=6;
temp:=array[0]; temp:=20;
array[0]:=array[i]; array[0]:=7;
array[i]:=temp; array[6]:=20;
array = { 7, 8, 18, 10, 6, 15, 20, 23}.
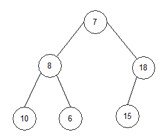
2.1) j=2, end=6, start=2.
root:=2; l_s:=5; r_s:=6;
Перевіряємо, чи r_s<end? 6<6? Нi.
Перевіряємо, чи l_s<end? 5<6? Так.
Перевіряємо array[root]<array[l_s]? 18<15. Нi.
Не змiнюємо масив.
2.2) j=1, end=6, start=1.
root:=1; l_s:=3; r_s:=4;
Перевіряємо, чи r_s<end? 4<6? Так.
Перевіряємо array[root]<array[r_s]? 8<6. Нi.
Перевіряємо array[root]<array[l_s]? 8<10. Так.
Перевіряємо array[l_s]<array[r_s]? 10<6. Нi.
Перевіряємо array[r_s]<array[l_s]? 6<10. Так.
temp:=array[root]; temp:=8;
array[root]:=array[l_s]; array[1]:=10;
array[l_s]:=temp; array[3]:=8;
array = { 7, 10, 18, 8, 6, 15, 20, 23}.
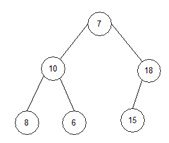
2.3) j=0, end=6, start=0.
root:=0; l_s:=1; r_s:=2;
Перевіряємо, чи r_s<end? 1<6? Так.
Перевіряємо array[root]<array[r_s]? 1<9. Так.
Перевіряємо array[l_s]<array[r_s]? 10<18. Так.
temp:=array[root]; temp:=7;
array[root]:=array[l_s]; array[0]:=18;
array[l_s]:=temp; array[2]:=7;
array = { 18, 10, 7, 8, 6, 15, 20, 23}.
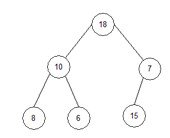
3) i=5;
temp:=array[0]; temp:=9;
array[0]:=array[i]; array[0]:=7;
array[i]:=temp; array[5]:=18;
array = { 7, 5, 1, 3, 0, 18, 20, 23}.
3.1) j=1, end=5, start=1.
root:=1; l_s:=3; r_s:=4;
Перевіряємо, чи r_s<end? 4<5? Так.
Перевіряємо array[root]<array[l_s]? 10<8. Нi.
Перевіряємо array[root]<array[r_s]? 10<6. Нi.
Не змiнюємо масив.
3.2) j=0, end=5, start=0.
root:=0; l_s:=1; r_s:=2;
Перевіряємо, чи r_s<end? 2<5? Так.
Перевіряємо array[root]<array[l_s]? 15<10. Нi.
Перевіряємо array[root]<array[r_s]? 15<7. Нi.
Не змiнюємо масив.
4) i=4;
temp:=array[0]; temp:=15;
array[0]:=array[i]; array[0]:=6;
array[i]:=temp; array[4]:=15;
array = { 6, 10, 7, 8, 15, 18, 20, 23}.
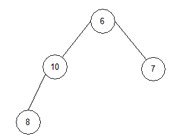
4.1) j=1, end=4, start=1.
root:=1; l_s:=3; r_s:=4;
Перевіряємо, чи r_s<end? 4<4? Нi.
Перевіряємо, чи l_s<end? 3<4? Так.
Перевіряємо array[l_s]>array[root]? 8>10. Нi.
Не змiнюємо масив.
4.2) j=0, end=4, start=0.
root:=0; l_s:=1; r_s:=2;
Перевіряємо, чи r_s<end? 2<4? Так.
Перевіряємо array[root]<array[r_s]? 7<6. Нi.
Перевіряємо array[r_s]<array[l_s]? 7<10. Так.
temp:=array[root]; temp:=6;
array[root]:=array[l_s]; array[0]:=10;
array[l_s]:=temp; array[1]:=6;
array = { 10, 6, 7, 8, 15, 18, 20, 23}.
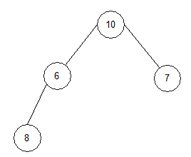
4) i=3;
temp:=array[0]; temp:=10;
array[0]:=array[i]; array[0]:=8;
array[i]:=temp; array[3]:=10;
array = { 8, 6, 7, 10, 15, 18, 20, 23}.
4.1) j=0, end=3, start=0.
root:=0; l_s:=1; r_s:=2;
Перевіряємо, чи r_s<end? 2<3? Так.
Перевіряємо array[root]<array[l_s]? 3<0. Нi.
Перевіряємо array[root]<array[r_s]? 3<1. Нi.
Не змiнюємо масив.
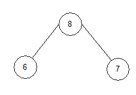
5) i=2;
temp:=array[0]; temp:=8;
array[0]:=array[i]; array[0]:=7;
array[i]:=temp; array[2]:=8;
array = { 7, 6, 8, 10, 15, 18, 20, 23}.
5.1) j=0, end=2, start=0.
root:=0; l_s:=1; r_s:=2;
Перевіряємо, чи r_s<end? 2<2? Нi.
Перевіряємо, чи l_s<end? 1<2? Так.
Перевіряємо array[l_s]>array[root]? 6>7. Нi.
Не змiнюємо масив.
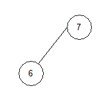
6) i=1;
temp:=array[0]; temp:=7;
array[0]:=array[i]; array[0]:=6;
array[i]:=temp; array[1]:=7;
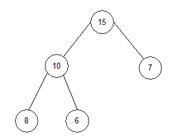
array = { 6, 7, 8, 10, 15, 18, 20, 23}.
![]()
Крок 5. Виведення результату: array = { 6, 7, 8, 10, 15, 18, 20, 23}
2.7 Оцінка ефективності алгоритму
Пірамідальне сортування – однин з найшвидших алгоритмів сортування, так як на кожному кроці потрібно максимум log2n обмінів, необхідних для відновлення структури піраміди. При сортуванні n елементів , оцінка складності алгоритму - О(n*log(n)). Даний алгоритм має сенс застосування лише на великих обсягах даних від 500-1000 елементів. Тільки в цьому випадку можна побачити виграш алгоритму в ефективності. Для менших обсягів даних він малопридатний.
3 Синтез машини Тьюрінга
3.1 Загальні відомості
Машина Тьюрінга - це кінцевий автомат, забезпечений безкінченою стрічкою і читаючою/записуючою голівкою (просто голівкою). Як і автомат, машина Тюрінга описується п'ятіркою (X, Y, Q δ, λ). Тут:
Х={x0, x1, x2 ., xn} - вхідний алфавіт, що містить порожню букву x0;
Y={y0, y1, y2.,yn} - вихідний алфавіт;
Q={q0, q1, q2 ., qm} - безліч внутрішніх достатків, причому q0 - Стоп-стан (у цьому стані машина Тюрінга не працює);
δ: QX →Q -функція переходів в наступний стан;
λ: QX →Y -функція виходів.
У свою чергу, Y=XU, де U={R, L, S}- команда на переміщення голівки: R – зрушитися вправо, L – зрушитися вліво, S – стояти на місці.
3.2 Постановка завдання
Необхідно синтезувати машину Тюрінга, яка копіює системи чисел (x1,x2,…,xn). В результаті роботи даної машини Тьюрінга необхідно отримати систему чисел (x1,x2,…,xn,x1,x2,…,xn).
3.3 Метод розв’язування
Числа x1,x2,…,xn – невід’ємні числа, які розташовані на стрічці у цьому ж порядку і є послідовністю з одиниць. Числа розділені нулем. Всі інші комірки стрічки, обмеженої зліва, також є нулями. Результат обчислень буде розміщений справа від числа xn, відокремлений від нього нулем.
Початкове положення голівки – на першій одиниці числа x1.Спочатку нам треба скопіювати першу одиницю числа x1 за числом xn. Для цього ми записуємо замість першої одиниці числа x1 нуль, та переносимо одиницю на 2 клітинки вліво. Тепер проходимо вправо та після останньої одиниці числа xn пропускаємо дві клітинки (два нулі) та дублюємо нашу одиницю.
Вертаємося вліво до першої лівої недубльованої одиниці x1,x2,…,xn, переносимо її на дві клітинки вліво, ідемо в кінець направо і записуємо одиницю. Аналогічно послідовно дублюємо всі одиниці з x1,x2,…,xn.
В кінці дублювання одержимо два блоки x1,x2,…,xn, розділених між собою чотирма нулями. Для того, щоб одержані послідовності були розділені одним нулем, зміщуємо першу послідовність x1,x2,…,xn на 3 клітинки вправо.
Треба врахувати можливу аварійну ситуацію, якщо початкове положення голівки – не на одиниці.
3.4 Словесний опис алгоритму
1 Початок копіювання числа x1 за число xn. Символ «1» помічаємо символом «0». Якщо «0» - Error(qEr).
2-3 Перехід на дві клітинки вліво. Запис «1».
4-5 Перехід на три клітинки вправо.
6-7 Прохід вправо залишку від чисел x1,x2,…,xn поки не зустрінемо «00». Переходимо праворуч.
8 Записуємо «1»
9-10 Прохід вліво копії чисел x1,x2,…,xn поки не зустрінемо «00». Переходимо ліворуч.
11 Якщо «1», то йдемо вліво, якщо «0» - знайшли «000», дублювання закінчено, перехід у п.30
12-13 Прохід вліво залишку від чисел x1,x2,…,xn поки не зустрінемо «00». Переходимо ліворуч.
14 Якщо «1», записуємо в кінець дублю x1,x2,…,xn символ «1», перехід у п.22. якщо «0» - записуємо в кінець дублю x1,x2,…,xn символи «01»
15-16 Записуємо символ «1», двічі переходимо праворуч
17 Символ «1» помічаємо символом «0».
18-19 Прохід вправо залишку від чисел x1,x2,…,xn поки не зустрінемо «00». Переходимо праворуч.
20-21 Прохід вправо копії від чисел x1,x2,…,xn поки не зустрінемо «00», перехід у п.8.
22-23 Записуємо символ «1», двічі переходимо праворуч
24 Символ «1» помічаємо символом «0».
25-26 Прохід вправо залишку від чисел x1,x2,…,xn поки не зустрінемо «00». Переходимо праворуч.
27-28 Прохід вправо копії від чисел x1,x2,…,xn поки не зустрінемо «00»,
29 Перехід вліво, перехід у п.8.
30 Зміщуємо початкові дані на 3 клітинки вправо Пропускаємо вліво всі «0».
31 Якщо «1», символ «1» помічаємо символом «0», якщо «0» зміщення закінчене, перехід у п.38.
32-33 Проходимо вправо два символи «0».
34 Символ «0» помічаємо символом «1»
35-37 Проходимо вліво три символи «0».
38 Якщо «1», символ «1» помічаємо символом «0» перехід у п.32, якщо «0» переводимо праворуч.
39 Якщо «1» - кінець роботи (q0), якщо «0», йдемо ліворуч доки не станемо на символ «1».
q0 – кінець роботи машини Тюрінга.
qEr – аварійне зупинення.
3.5 Символи вхідного та вихідного алфавіту
X![]() { 0, 1};
{ 0, 1};
Y![]() { 0, 1, Er };
{ 0, 1, Er };
3.6 Схема алгоритму машини Тьюрінга
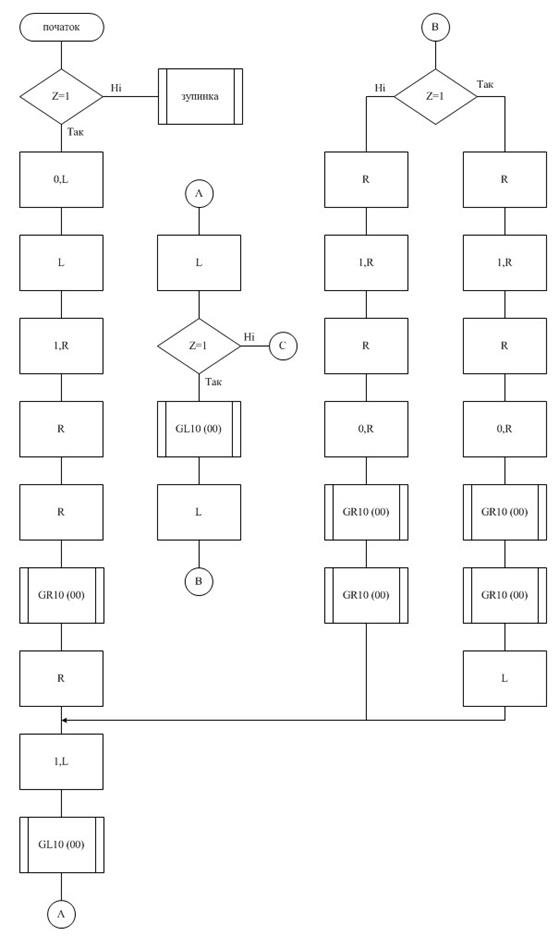
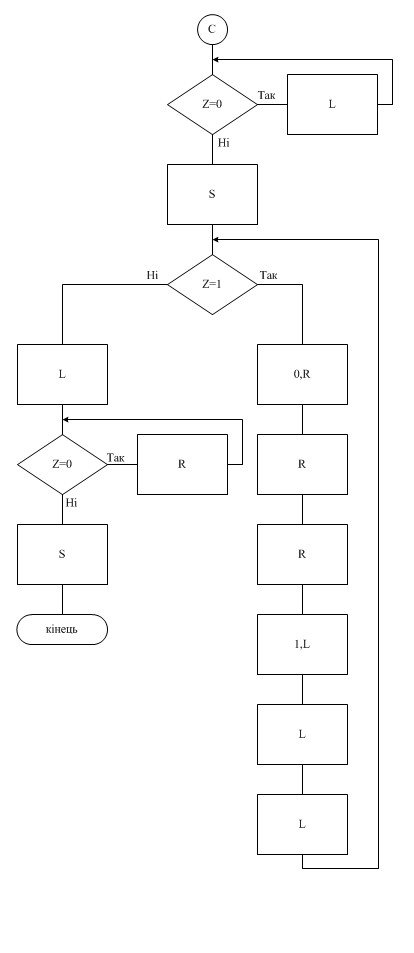
3.7 Коригування результату
Коригування результату роботи не потрібно.
3.8 Стандартна конфігурація
Голівка встановлена на першій одиниці числа x1.
3.9 Функціональна схема машини Тьюрінга
| Q | 0 | 1 | |
| Q1 | 0SQEr | 0LQ2 | - (0) авар. зуп. (головка не на 1) / (1) видалення «одиниці» з першого числа |
| Q2 | 0LQ3 | - перехід ліворуч | |
| Q3 | 1RQ4 | - запис видаленої «одиниці» з першого числа | |
| Q4 | 0RQ5 | - перехід праворуч | |
| Q5 | 0RQ6 | - перехід праворуч | |
| Q6 | 0RQ7 | 1RQ6 | - пропуск числа |
| Q7 | 0RQ8 | 1RQ6 | - (0) знайшли «00» / (1) пропуск наступного числа, перехід на q6 |
| Q8 | 1LQ9 | - дублюємо «одиницю» з числа | |
| Q9 | 0LQ10 | 1LQ9 | - пропуск числа |
| Q10 | 0LQ11 | 1LQ9 | - (0) знайшли «00» / (1) пропуск наступного числа, перехід на q9 |
| Q11 | 0LQ30 | 1LQ12 | - (0) знайшли «000», дублювання закінчено, змістимо початкові дані на 3 клітинки праворуч, перехід на q30 / (1) перехід на q12 |
| Q12 | 0LQ13 | 1LQ12 | - пропуск числа |
| Q13 | 0LQ14 | 1LQ12 | - (0) знайшли «00» / (1) пропуск наступного числа, перехід на q12 |
| Q14 | ORQ15 | 1RQ22 | - (0) дублюємо «01» перехід на q15/ (1) дублюємо «одиницю» перехід на q22 |
| Q15 | 1RQ16 | - переносимо «одиницю» | |
| Q16 | 0RQ17 | - перехід праворуч | |
| Q17 | 0RQ18 | - видалення «одиниці» | |
| Q18 | 0RQ19 | 1RQ19 | - пропуск числа |
| Q19 | 0RQ20 | 1RQ19 | - (0) знайшли «00» / (1) пропуск наступного числа, перехід на q19 |
| Q20 | 0RQ21 | 1RQ20 | - пропуск числа |
| Q21 | 0SQ8 | 1RQ20 | - (0) знайшли «00» перехід на q8 / (1) пропуск наступного числа, перехід на q20 |
| Q22 | 1RQ23 | - переносимо «одиницю» | |
| Q23 | 0RQ24 | - перехід праворуч | |
| Q24 | 0RQ25 | - видалення «одиниці» | |
| Q25 | 0RQ26 | 1RQ25 | - пропуск числа |
| Q26 | 0RQ27 | 1RQ25 | - (0) знайшли «00» / (1) пропуск наступного числа, перехід на q25 |
| Q27 | 0RQ28 | 1RQ27 | - пропуск числа |
| Q28 | 0LQ8 | 1RQ27 | - (0) знайшли «00» перехід на q8 / (1) пропуск наступного числа, перехід на q27 |
| Q30 | 0LQ30 | 1SQ31 | - (0) пропускаємо нулі / (1) перехід на q31 |
| Q31 | 0LQ38 | 0RQ32 | - (0) знайшли «0» перехід на q38 / (1) видаляємо «одиницю» |
| Q32 | 0RQ33 | - перехід праворуч | |
| Q33 | 0RQ34 | - перехід праворуч | |
| Q34 | 1LQ35 | - переносимо «одиницю» | |
| Q35 | 0LQ36 | - перехід ліворуч | |
| Q36 | 0LQ37 | - перехід ліворуч | |
| Q37 | 0LQ31 | - перехід ліворуч | |
| Q38 | 0RQ39 | 0RQ32 | - (0) знайшли «00» перехід на q39 / (1) видаляємо «одиницю», перехід на q32 |
| Q39 | 0RQ39 | 1SQ0 | - (0) пропускаємо нулі / (1) головку встановлено на першу «одиницю» |
| Q0 | 0SQ0 | 1SQ0 | - кінець роботи |
| QEr | 0SQEr | 1SQEr | - аварійна зупинка |
3.10 Контрольний приклад
1) 1
| q1: | 0…00010000000… |
| q2: | 0…00000000000… |
| q3: | 0…00000000000… |
| q4: | 0…01000000000… |
| q5: | 0…01000000000… |
| q6: | 0…01000000000… |
| q7: | 0…01000000000… |
| q8: | 0…01000000000… |
| q9: | 0…01000010000… |
| q10: | 0…01000010000… |
| q11: | 0…01000010000… |
| q30: | 0…01000010000… |
| q30: | 0…01000010000… |
| q31: | 0…01000010000… |
| q32: | 0…00000010000… |
| q33: | 0…00000010000… |
| q34: | 0…00000010000… |
| q35: | 0…00001010000… |
| q36: | 0…00001010000… |
| q37: | 0…00001010000… |
| q31: | 0…00001010000… |
| q38: | 0…00001010000… |
| q39: | 0…00001010000… |
| q39: | 0…00001010000… |
| q0: | 0…00001010000… |
Кінець роботи.
Результат 1 1.
2) 111
| q1: | 0…00001110000000… |
| q2: | 0…00000110000000… |
| q3: | 0…00000110000000… |
| q4: | 0…00100110000000… |
| q5: | 0…00100110000000… |
| q6: | 0…00100110000000… |
| q6: | 0…00100110000000… |
| q7: | 0…00100110000000… |
| q8: | 0…00100110000000… |
| q9: | 0…00100110010000… |
| q10: | 0…00100110010000… |
| q11: | 0…00100110010000… |
| q12: | 0…00100110010000… |
| q12: | 0…00100110010000… |
| q13: | 0…00100110010000… |
| q14: | 0…00100110010000… |
| q22: | 0…00100110010000… |
| q23: | 0…00110110010000… |
| q24: | 0…00110110010000… |
| q25: | 0…00110010010000… |
| q25: | 0…00110010010000… |
| q26: | 0…00110010010000… |
| q27: | 0…00110010010000… |
| q27: | 0…00110010010000… |
| q28: | 0…00110010010000… |
| q8: | 0…00110010010000… |
| q9: | 0…00110010011000… |
| q9: | 0…00110010011000… |
| q10: | 0…00110010011000… |
| q11: | 0…00110010011000… |
| q12: | 0…00110010011000… |
| q13: | 0…00110010011000… |
| q14: | 0…00110010011000… |
| q22: | 0…00110010011000… |
| q23: | 0…00111010011000… |
| q24: | 0…00111010011000… |
| q25: | 0…00111000011000… |
| q26: | 0…00111000011000… |
| q27: | 0…00111000011000… |
| q27: | 0…00111000011000… |
| q28: | 0…00111000011000… |
| q8: | 0…00111000011000… |
| q9: | 0…00111000011100… |
| q9: | 0…00111000011100… |
| q10: | 0…00111000011100… |
| q11: | 0…00111000011100… |
| q30: | 0…00111000011100… |
| q30: | 0…00111000011100… |
| q31: | 0…00111000011100… |
| q32: | 0…00110000011100… |
| q33: | 0…00110000011100… |
| q34: | 0…00110000011100… |
| q35: | 0…00110001011100… |
| q36: | 0…00110001011100… |
| q37: | 0…00110001011100… |
| q31: | 0…00110001011100… |
| q32: | 0…00100001011100… |
| q33: | 0…00100001011100… |
| q34: | 0…00100001011100… |
| q35: | 0…00100011011100… |
| q36: | 0…00100011011100… |
| q37: | 0…00100011011100… |
| q31: | 0…00100011011100… |
| q32: | 0…00000011011100… |
| q33: | 0…00000011011100… |
| q34: | 0…00000011011100… |
| q35: | 0…00000111011100… |
| q36: | 0…00000111011100… |
| q37: | 0…00000111011100… |
| q31: | 0…00000111011100… |
| q38: | 0…00000111011100… |
| q39: | 0…00000111011100… |
| q39: | 0…00000111011100… |
| q0: | 0…00000111011100… |
Кінець роботи.
Результат 111 111.
3) 11 1
| q1: | 0…0000110100000000… |
| q2: | 0…0000010100000000… |
| q3: | 0…0000010100000000… |
| q4: | 0…0010010100000000… |
| q5: | 0…0010010100000000… |
| q6: | 0…0010010100000000… |
| q6: | 0…0010010100000000… |
| q6: | 0…0010010100000000… |
| q7: | 0…0010010100000000… |
| q6: | 0…0010010100000000… |
| q7: | 0…0010010100000000… |
| q8: | 0…0010010100000000… |
| q9: | 0…0010010100100000… |
| q10: | 0…0010010100100000… |
| q11: | 0…0010010100100000… |
| q12: | 0…0010010100100000… |
| q13: | 0…0010010100100000… |
| q12: | 0…0010010100100000… |
| q13: | 0…0010010100100000… |
| q14: | 0…0010010100100000… |
| q22: | 0…0010010100100000… |
| q23: | 0…0011010100100000… |
| q24: | 0…0011010100100000… |
| q25: | 0…0011000100100000… |
| q26: | 0…0011000100100000… |
| q25: | 0…0011000100100000… |
| q26: | 0…0011000100100000… |
| q27: | 0…0011000100100000… |
| q27: | 0…0011000100100000… |
| q28: | 0…0011000100100000… |
| q8: | 0…0011000100100000… |
| q9: | 0…0011000100110000… |
| q9: | 0…0011000100110000… |
| q10: | 0…0011000100110000… |
| q11: | 0…0011000100110000… |
| q12: | 0…0011000100110000… |
| q13: | 0…0011000100110000… |
| q14: | 0…0011000100110000… |
| q15: | 0…0011000100110000… |
| q16: | 0…0011010100110000… |
| q17: | 0…0011010100110000… |
| q18: | 0…0011010000110000… |
| q19: | 0…0011010000110000… |
| q20: | 0…0011010000110000… |
| q20: | 0…0011010000110000… |
| q21: | 0…0011010000110000… |
| q8: | 0…0011010000110000… |
| q9: | 0…0011010000110100… |
| q10: | 0…0011010000110100… |
| q9: | 0…0011010000110100… |
| q9: | 0…0011010000110100… |
| q10: | 0…0011010000110100… |
| q11: | 0…0011010000110100… |
| q30: | 0…0011010000110100… |
| q30: | 0…0011010000110100… |
| q31: | 0…0011010000110100… |
| q32: | 0…0011000000110100… |
| q33: | 0…0011000000110100… |
| q34: | 0…0011000000110100… |
| q35: | 0…0011000010110100… |
| q36: | 0…0011000010110100… |
| q37: | 0…0011000010110100… |
| q31: | 0…0011000010110100… |
| q38: | 0…0011000010110100… |
| q32: | 0…0010000010110100… |
| q33: | 0…0010000010110100… |
| q34: | 0…0010000010110100… |
| q35: | 0…0010001010110100… |
| q36: | 0…0010001010110100… |
| q37: | 0…0010001010110100… |
| q31: | 0…0010001010110100… |
| q32: | 0…0000001010110100… |
| q33: | 0…0000001010110100… |
| q34: | 0…0000001010110100… |
| q35: | 0…0000011010110100… |
| q36: | 0…0000011010110100… |
| q37: | 0…0000011010110100… |
| q31: | 0…0000011010110100… |
| q38: | 0…0000011010110100… |
| q39: | 0…0000011010110100… |
| q39: | 0…0000011010110100… |
| q0: | 0…0000011010110100… |
Кінець роботи.
Результат 11 1 11 1.
Висновок
Підводячи підсумок, скажімо, що в даній роботі описані одні з найбільш ефективних алгоритмів пошуку найкоротшого шляху від однієї вершини неорієнтованого графа до всіх інших вершин графа методом Дейкстри та алгоритм пірамідального сортування. Хоч ці алгоритми і були розроблені досить давно, вони усе одно залишаються ефективними і активно застосовуються на практиці. При вирішенні поставлених завдань були використані різні структури даних наприклад, масиви. У вигляді масивів ми представляли вектора активності при знаходженні найкоротшого шляху. Для застосування пірамідальної сортування ми використовували піраміду, однак, в пам'яті подану як масив.
Також була розроблена машини Тюрінга, яка копіює системи чисел (x1,x2,…,xn), при виконанні роботи якої одержимо (x1, x2, …, xn, x1, x2, …, xn). Хоч вона і не має ніякого практичного застосування при програмуванні, вона дає поняття про те, як розбивати складне завдання на більш дрібні і легкі.
Список літератури
1. Паулин О. Н. Основы теории алгоритмов. Одесса, изд. «Автограф», 2001 -186 с.
2. Методические указания и задачи к практическим занятиям по курсу «Теория алгоритмов и вычислительных процессов» для студентов специальностей 7.080403 и 7.091501/ О.Н. Паулин, В.М. Рувинская, Е.С. Осадчук. Одесса ОГПУ, 1996 – Ч.1 – 54 с.
3. Единая система программной документации/ Схемы алгоритмов, программ, данных и систем. Условные обозначения и правила выполнения. ГОСТ 19.701-90 – М.:Госкомитет СССР по управлению качеством продукции и стандартизации, 1990 – 25 с.
Похожие материалы
... "ВНІЇЕМ-3", а також надшвидкодіюча БЕСМ-6 з продуктивністю 1 млн операцій в секунду. 2.3 Третє покоління комп'ютерів Поява інтегрованих схем започаткувала новий етап розвитку обчислювальної техніки - народження машин третього покоління. Інтегрована схема, яку також називають кристалом, являє собою мініатюрну електронну схему, витравлену на поверхні кремнієвого кристала площею приблизно 10 ...
... ці засоби.[9] 1.3. Журналістика, як інформаційний простір (Дивіться Додаток 2) Останнім часом у слововжиток міцно увійшло поняття інформаційного простору, під яким розуміють сукупність територій, охоплених засобами масової інформації певної категорії (регіональними, національними, світовими)[20;36]. Найчастіше цей термін вживають у значенні національного інформаційного простору, який ...





0 комментариев