Федеральное агентство связи
Московский технический университет связи и информатики
Кафедра технической электродинамики и антенн
Анализ Электромагнитного поля в прямоугольном волноводе
Проверил: Выполнил:
Доцент кафедры ТЭДиА Студент группы БРТ1302
Муравцов А.Д. Звездинов Виктор.
Москва 2015
Техническое задание
В полой трубе прямоугольного сечения (Рис. 1) с идеально проводящими стенками создано монохроматическое электромагнитное поле. Труба заполнена однородной изотропной средой без потерь, абсолютная диэлектрическая и магнитная проницаемости равны ![]() и
и ![]() соответственно. Известно, что комплексная амплитуда вектора
соответственно. Известно, что комплексная амплитуда вектора ![]() равна:
равна:
![]() , где
, где 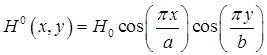 ,
, ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() - частота электромагнитных колебаний;
- частота электромагнитных колебаний; ![]() - длина волны, свободно распространяющейся в однородной изотропной непроводящей среде с параметрами
- длина волны, свободно распространяющейся в однородной изотропной непроводящей среде с параметрами ![]() и
и ![]() ;
; ![]() - скорость света в этой среде,
- скорость света в этой среде, ![]() ,
, ![]()
Исходные данные:
| № вар |
В/м |
|
| a см | b см |
|
ГГц |
ГГц |
| 2 | 100 | 2,25 | 1 | 6 | 4 | 0,75 | 4 | 2 |
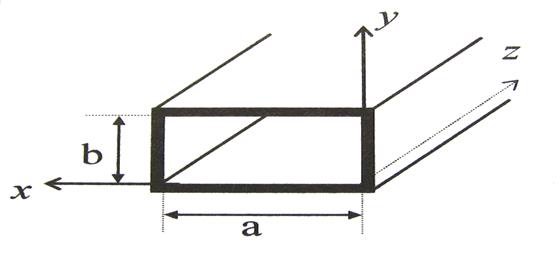

Рис. 1
1)Определение комплексных амплитуд поперечных составляющих вектора ![]() , а затем из уравнений Максвелла определим комплексные амплитуды составляющих вектора
, а затем из уравнений Максвелла определим комплексные амплитуды составляющих вектора ![]() , используя соотношение
, используя соотношение
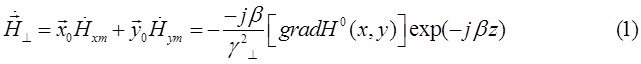 ,
,
Найдем комплексные амплитуды составляющих вектора ![]() , воспользовавшись вышеприведённым соотношением:
, воспользовавшись вышеприведённым соотношением:
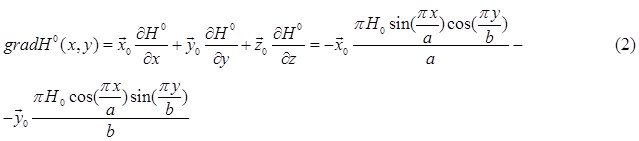
Подставляя значение из (2) в (1) найдём комплексную форму вектора ![]() :
:
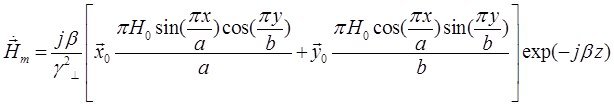
Запишем проекции комплексной амплитуды вектора ![]() на оси координат:
на оси координат:
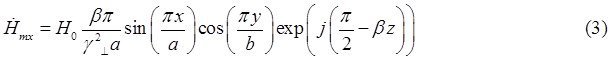
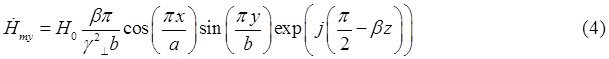
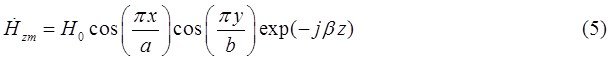
Воспользуемся первым уравнением Максвелла в комплексной форме для определения комплексной амплитуды вектора ![]() :
:
![]() , где
, где ![]() - абсолютная диэлектрическая проницаемость среды,
- абсолютная диэлектрическая проницаемость среды, ![]() ,
, ![]() – частота электромагнитных колебаний, тогда отсюда
– частота электромагнитных колебаний, тогда отсюда ![]()
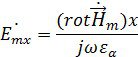
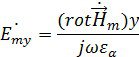
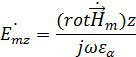
Найдем ![]() :
:
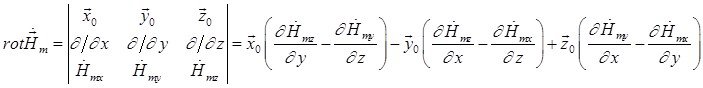
Тогда составляющие комплексной амплитуды вектора ![]() равны соответственно:
равны соответственно:
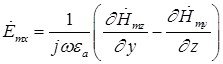 (7)
(7)
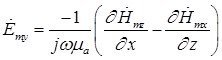 (8)
(8)
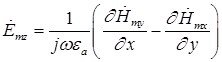
(9)
Найдем выражения для частных производных составляющих комплексной амплитуды вектора ![]() по соответствующим координатам:
по соответствующим координатам:
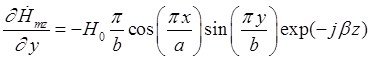
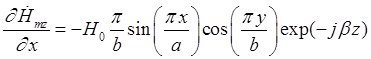
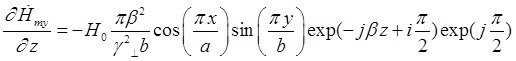
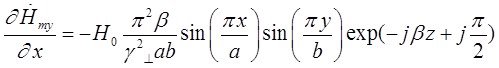
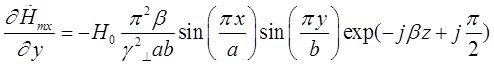
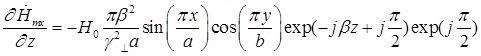
Подставляя найденные значения частных производных в (7), (8) и (9), получим итоговые выражения для комплексных амплитуд составляющих вектора ![]() :
:
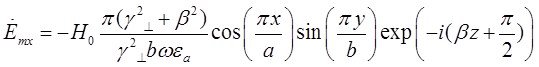 (10)
(10)
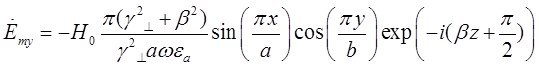 (11)
(11)
![]() (12)
(12)
2)Определение диапазона частот, в котором ![]() – действительное число, т.е. рассматриваемое поле – бегущая волна.
– действительное число, т.е. рассматриваемое поле – бегущая волна.
По условию задачи ![]() . Значит,
. Значит, ![]() будет действительным в случае, если
будет действительным в случае, если
![]() , т.е. при
, т.е. при ![]()
![]()
Этому диапазону длин волн соответствует диапазон частот:
![]() , где
, где 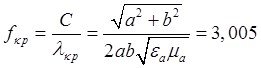 ГГц, где С =
ГГц, где С = ![]() ,
,
![]()
![]()
Таким образом, если частота волны не принадлежит рассчитанному диапазону частот, то ![]() является мнимой величиной. Для этого случая произведем замену:
является мнимой величиной. Для этого случая произведем замену: ![]() , при этом
, при этом ![]() ,
, ![]()
3) Определение мгновенных значений всех составляющих векторов![]() и
и ![]() для двух случаев:
для двух случаев:
а) когда ![]() принадлежит найденному в п. 2 диапазону частот
принадлежит найденному в п. 2 диапазону частот
б) когда ![]() не принадлежит этому диапазону.
не принадлежит этому диапазону.
Для получения выражений для мгновенных значений составляющих векторов поля необходимо домножить их комплексные амплитуды на выражение ![]() и, выделить действительную часть, то есть:
и, выделить действительную часть, то есть:
![]() ;
; ![]()
В первом случае выражения для комплексных амплитуд составляющих остаются без изменений. Во втором случае необходимо произвести замену, описанную в п. 2.
При ![]() выражения для комплексны амплитуд составляющих магнитного и электрического полей имеют вид:
выражения для комплексны амплитуд составляющих магнитного и электрического полей имеют вид:
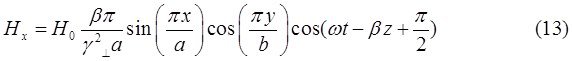
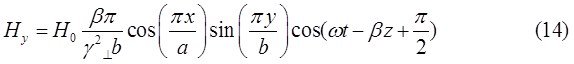
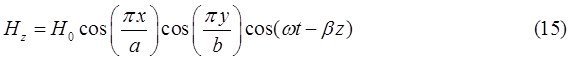
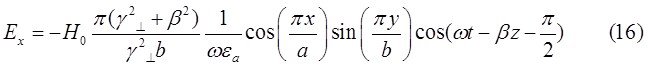
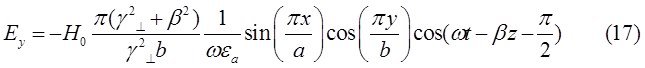
![]()
(18)
При ![]() выражения для комплексны амплитуд составляющих магнитного и электрического полей имеют вид:
выражения для комплексны амплитуд составляющих магнитного и электрического полей имеют вид:
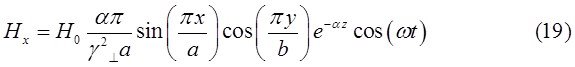
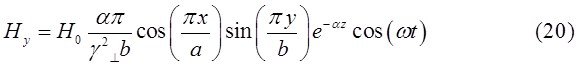
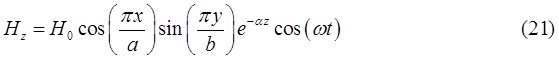
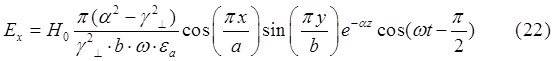
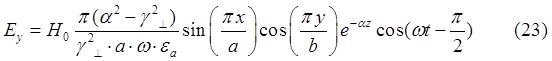
![]() (24)
(24)
4)Построение графиков зависимостей амплитуд составляющих векторов поля на частотах ![]() и
и ![]() по данным приведенным, в таблице технического задания
по данным приведенным, в таблице технического задания
Вычислим постоянные множители в математическом пакете MathCAD 14, а затем подставим соответствующие значения постоянных величин в выражения с (13) по (24):
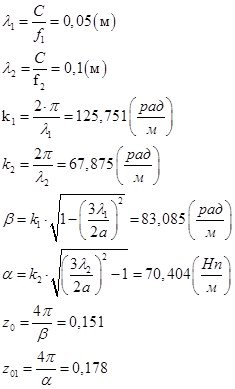 |
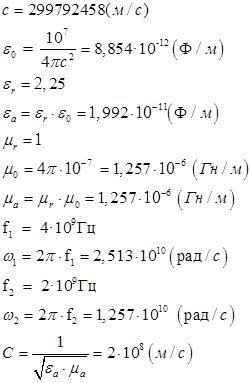
Определение амплитуд составляющих электрического и магнитного полей для Случая 1:
z=z0; y=0,5b; ![]() ;
; ![]()
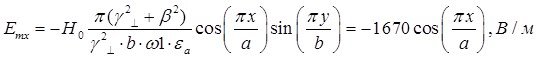
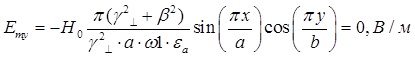
![]()
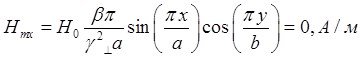
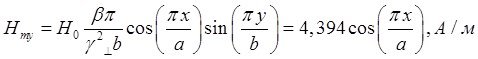
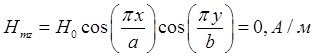
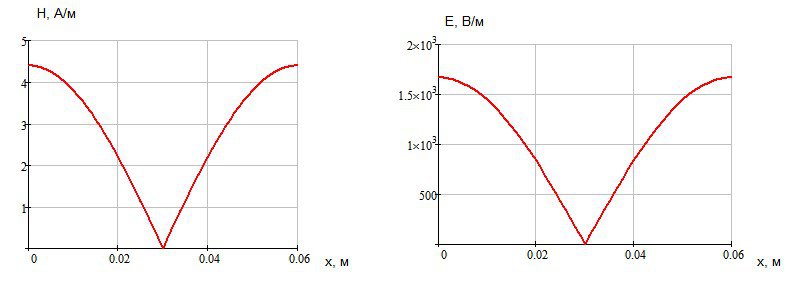
Указанные формулы были запрограммированы в математическом пакете MathCAD 14, где были построены графики данных зависимостей. Результаты показаны на Рис. 2, Рис. 3.
Определение амплитуд составляющих электрического и магнитного полей для Случая 2:
z=z0; y=0,5b; ![]() ;
; ![]()
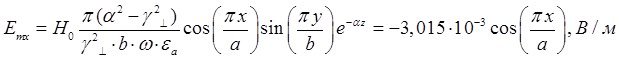
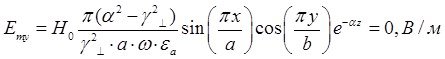
![]()
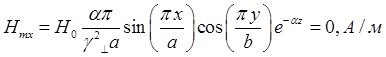
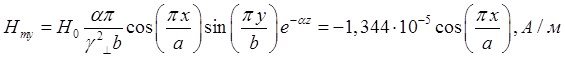
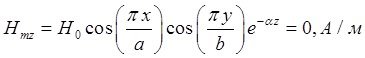
Указанные формулы были запрограммированы в математическом пакете MathCAD 14, где были построены графики данных зависимостей. Результаты показаны на Рис. 4, Рис. 5.
Определение амплитуд составляющих электрического и магнитного полей для Случая 3:
z=z0; x=0,75a; ![]() ;
; ![]()
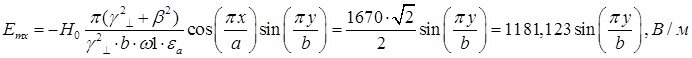
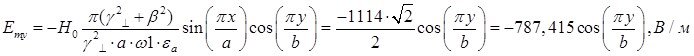
![]()
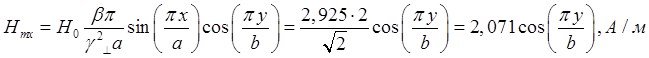
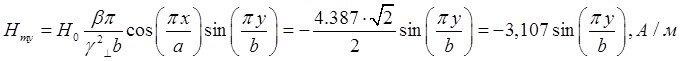
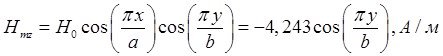
Указанные формулы были запрограммированы в математическом пакете MathCAD 14, где были построены графики данных зависимостей. Результаты показаны на Рис. 6, Рис. 7.
Определение амплитуд составляющих электрического и магнитного полей для Случая 4:
z=z0; x=0,75a; ![]() ;
; ![]()
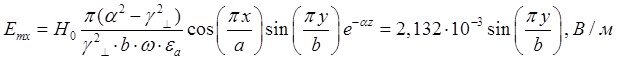
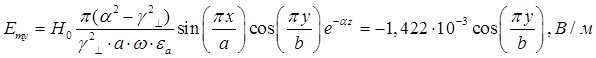
![]()
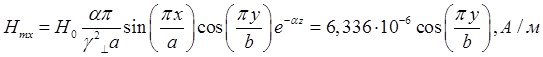
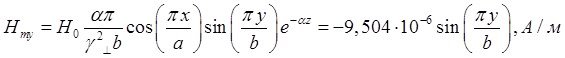
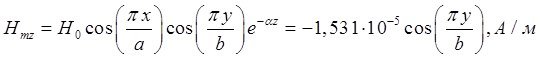
Указанные формулы были запрограммированы в математическом пакете MathCAD 14, где были построены графики данных зависимостей. Результаты показаны на Рис.8, Рис. 9.
Определение амплитуд составляющих электрического и магнитного полей для Случая 5:
x=0,25a; y=0,25b; ![]() ;
; ![]()
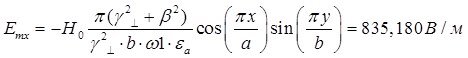
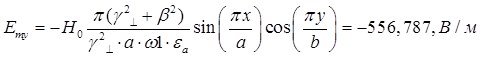
![]()
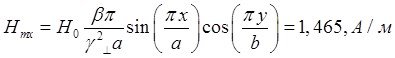
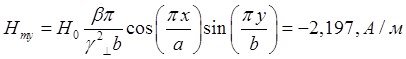
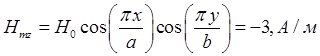
Указанные формулы были запрограммированы в математическом пакете MathCAD 14, где были построены графики данных зависимостей. Результаты показаны на Рис. 10, Рис. 11.
Определение амплитуд составляющих электрического и магнитного полей для Случая 6:
x=0,25a; y=0,25b; ![]() ;
; ![]()
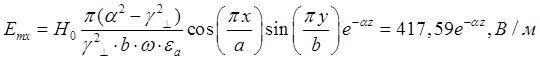
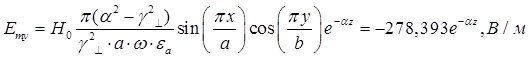
![]()
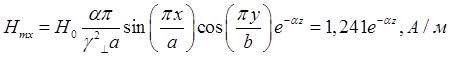
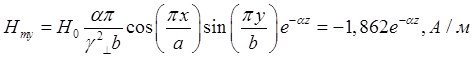
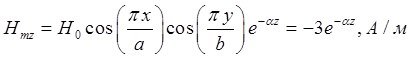
Указанные формулы были запрограммированы в математическом пакете MathCAD 14, где были построены графики данных зависимостей. Результаты показаны на Рис. 12, Рис. 13.
В выражениях для случаев 1, 3, 5 ![]() м,
м, ![]() рад/с, z0=0.151 м,
рад/с, z0=0.151 м, ![]() а для случаев. 2, 4, 6
а для случаев. 2, 4, 6 ![]() м,
м, ![]() рад/с, z0=0.178 м и
рад/с, z0=0.178 м и ![]() Нп/м.
Нп/м.
 ---
---
Рис. 2 Рис. 3
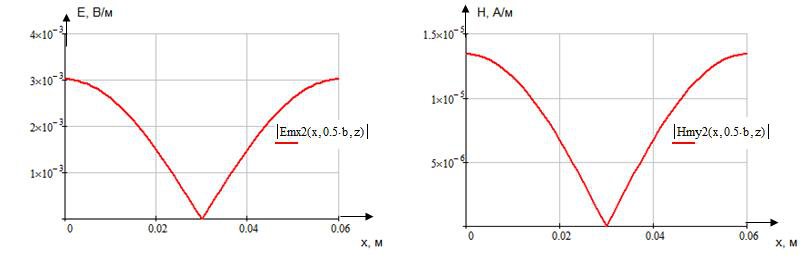
Рис. 4 Рис. 5
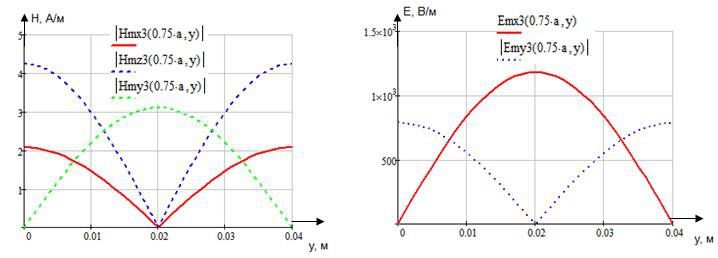
Рис. 6 Рис. 7
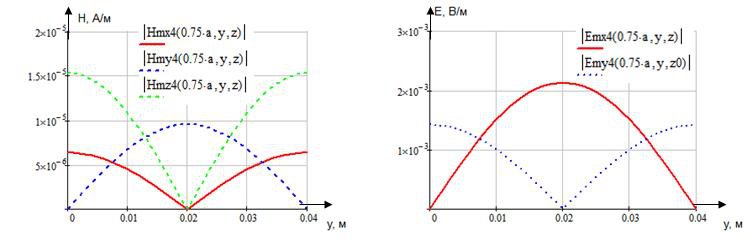
Рис. 8 Рис. 9
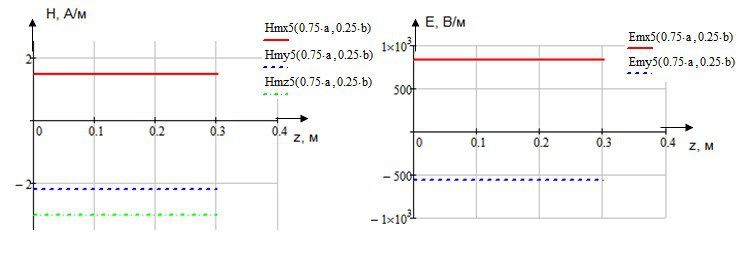
Рис. 10 Рис. 11
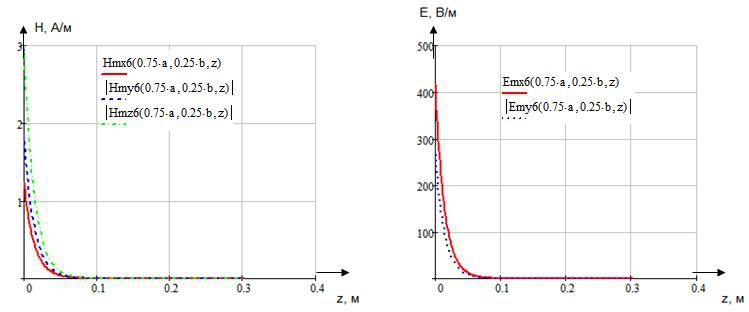
Рис. 12 Рис. 13
5)Проверка выполнения граничных условий для касательных составляющих вектора ![]() и нормальных составляющих вектора
и нормальных составляющих вектора ![]() на боковой (х=а) стенке трубы.
на боковой (х=а) стенке трубы.
Как известно на границе раздела двух сред – идеального металла и воздуха ![]() и
и![]() . Проверка граничных условий заключается в проверке истинности этих утверждений, т.е. равенства нулю касательной вектора
. Проверка граничных условий заключается в проверке истинности этих утверждений, т.е. равенства нулю касательной вектора ![]() и нормальной вектора
и нормальной вектора ![]() проекций (составляющих).
проекций (составляющих).
На боковой стенке (х=а) рассмотрению подлежат (17) и (13) составляющие:
Подставим в эти выражения х=а, получим:
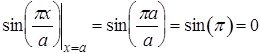 ,
,
При этом другие множители от координаты х не зависят. Следовательно, оба выражения обращаются в ноль и граничные условия выполняются.
6)Определить комплексные амплитуды плотностей поверхностных токов и зарядов на всех стенках трубы.
В случае идеально проводящих стенок токи проводимости являются поверхностными, а комплексную амплитуду поверхностного тока можно найти по формуле:
![]()
, где ![]() - нормаль (25)
- нормаль (25)
Комплексную амплитуду плотности зарядов можно найти по формуле:
![]() где
где ![]() - абсолютная диэлектрическая проницаемость (26)
- абсолютная диэлектрическая проницаемость (26)
Найдем комплексные амплитуды плотностей поверхностных токов и зарядов на всех стенках трубы:
1) Для нижней стенки трубы ![]() нормаль совпадает с вектором
нормаль совпадает с вектором ![]() :
: ![]() .
.
Касательными к этой стенке составляющими вектора ![]() являются составляющие вдоль осей x и z, то есть:
являются составляющие вдоль осей x и z, то есть:
![]()
Подставим это выражение в формулу (25):
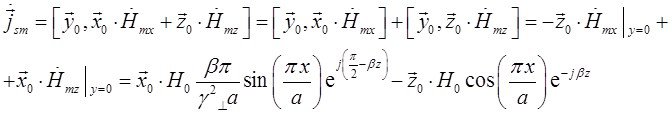
Нормальной к этой стенке составляющей вектора ![]() будет составляющая
будет составляющая ![]() . Тогда комплексная амплитуда плотности поверхностных зарядов по формуле (26) будет равна:
. Тогда комплексная амплитуда плотности поверхностных зарядов по формуле (26) будет равна:
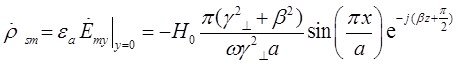
2) Для верхней стенки трубы ![]() нормаль противоположна вектору
нормаль противоположна вектору ![]() :
: ![]() .
.
Касательными к этой стенке составляющими вектора ![]() являются составляющие вдоль осей x и z, то есть:
являются составляющие вдоль осей x и z, то есть:
![]()
Подставим это выражение в формулу (25):
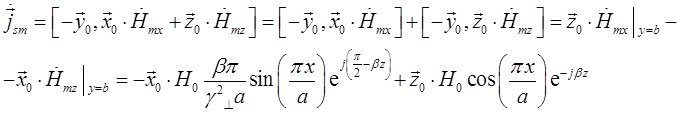
Нормальной к этой стенке составляющей вектора ![]() будет составляющая
будет составляющая ![]() . Комплексная амплитуда плотности поверхностных зарядов по формуле (26) будет равна:
. Комплексная амплитуда плотности поверхностных зарядов по формуле (26) будет равна:
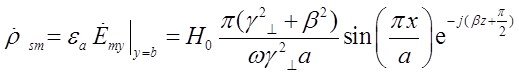
3) Для правой стенки трубы ![]() нормаль совпадает с вектором
нормаль совпадает с вектором ![]() :
: ![]() .
.
Касательными к этой стенке составляющими вектора ![]() являются составляющие вдоль осей y и z, то есть:
являются составляющие вдоль осей y и z, то есть:
![]()
Подставим это выражение в формулу (25):
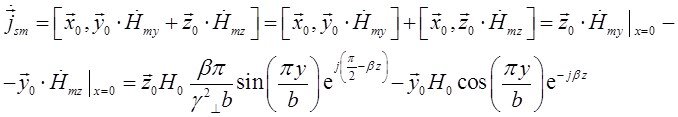
Нормальной к этой стенке составляющей вектора ![]() будет составляющая
будет составляющая ![]() . Комплексная амплитуда плотности поверхностных зарядов по формуле (26) будет равна:
. Комплексная амплитуда плотности поверхностных зарядов по формуле (26) будет равна:
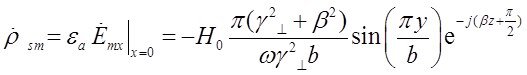
4) Для левой стенки трубы ![]() нормаль противоположна вектору
нормаль противоположна вектору ![]() :
: ![]() .
.
Касательными к этой стенке составляющими вектора ![]() , как и в третьем случае, являются составляющие вдоль осей y и z, то есть:
, как и в третьем случае, являются составляющие вдоль осей y и z, то есть:
![]()
Подставим это выражение в формулу (25):
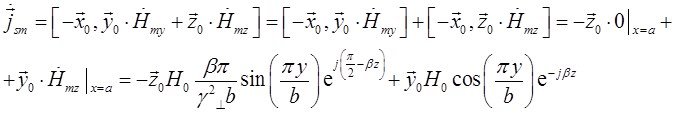
Нормальной к этой стенке составляющей вектора ![]() будет составляющая
будет составляющая ![]() . Комплексная амплитуда плотности поверхностных зарядов по формуле (26) будет равна:
. Комплексная амплитуда плотности поверхностных зарядов по формуле (26) будет равна:
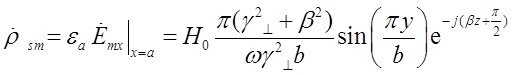
7)Записать выражения для комплексного вектора Пойтинга. Определение среднее за период значение плотности потока энергии и амплитуду плотности реактивного потока энергии.
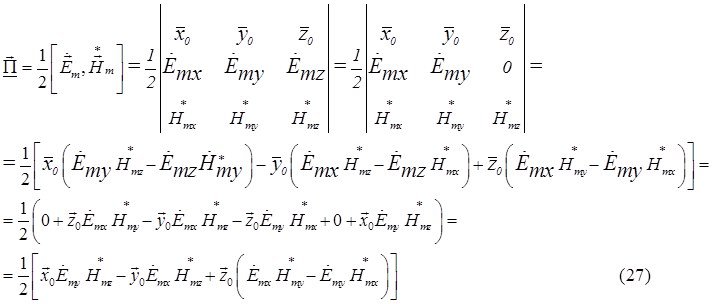 Где
Где ![]() – это комплексная амплитуда напряженности электрического поля, а
– это комплексная амплитуда напряженности электрического поля, а ![]() – это комплексно – сопряженная амплитуда напряженности магнитного поля.
– это комплексно – сопряженная амплитуда напряженности магнитного поля.
Рассмотрим режим бегущей волны ![]() :
:
Запишем выражения для сопряженных составляющих вектора ![]() :
:
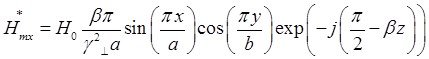
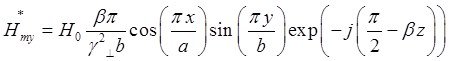
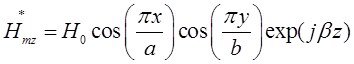
Найдём выражения для каждой из составляющих вектора Пойтинга, исходя из (27):
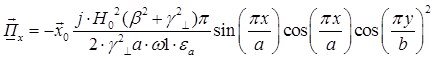
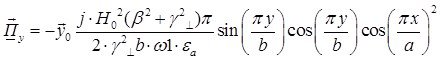
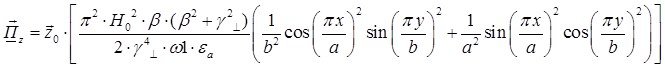
Тогда выражение для вектора Пойтинга примет вид:
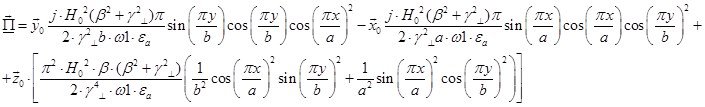
Cоставляющие по оси х и по оси у чисто мнимые, а составляющая по оси z – действительная, значит вдоль оси z происходит перенос энергии. Следовательно:
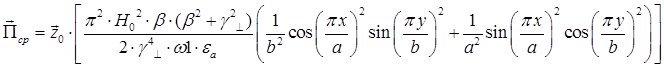
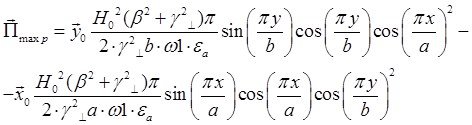
Рассмотрим режим стоячей волны ![]() :
:
Запишем выражения для сопряженных составляющих вектора ![]() :
:
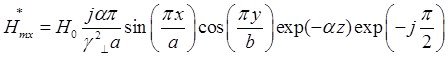
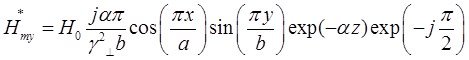
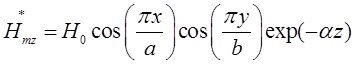
Найдём выражения для каждой из составляющих вектора Пойтинга, исходя из (27):
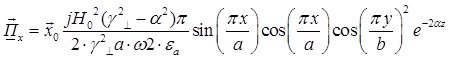
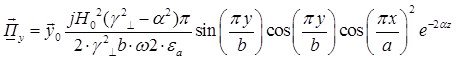
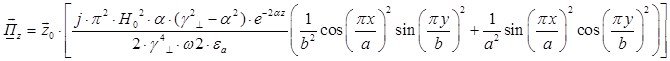
В этом случае вектор Пойтинга чисто мнимый и переноса энергии не происходит.
![]()
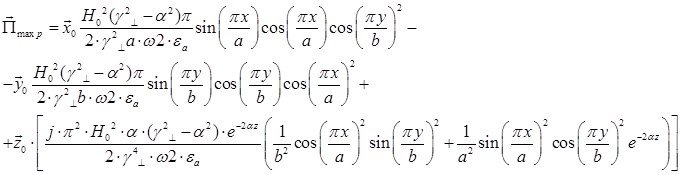
8)Вычисление среднего за период поток энергии через поперечное сечение трубы.
Проинтегрируем выражения для плотности активного потока энергии по площади поперечного сечения волновода:
Для этого проинтегрируем по площади поперечного сечения среднюю за период плотность потока энергии ![]() , определяемую выражением (27):
, определяемую выражением (27):
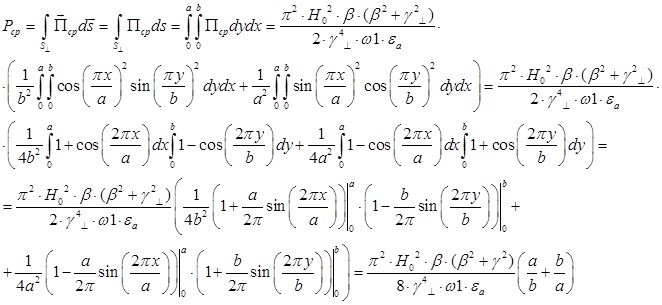
![]() Вт
Вт
9)Определение фазовой скорости Vф и скорости распространения энергии Vэ рассматриваемой волны. Расчет и построение графиков зависимостей Vф и Vэ от частоты.
За время ![]() волна распространяется на расстояние
волна распространяется на расстояние ![]() , при этом фазы волны в моменты времени
, при этом фазы волны в моменты времени ![]() и
и ![]() в плоскостях
в плоскостях ![]() и
и ![]() соответственно совпадают.
соответственно совпадают.
Рассчитаем фазовую скорость волны
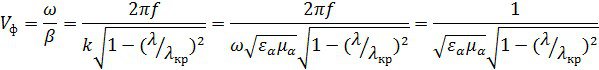
Где ![]()
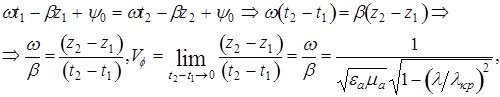
здесь ![]() – фаза в момент времени t=0.
– фаза в момент времени t=0.
Рассчитаем фазовую скорость волны с учетом ![]() м.
м.
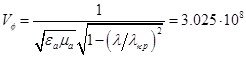 , м/с
, м/с
Для расчета скорость распространения энергии Vэ воспользуемся соотношением:
Vэ![]() Vэ
Vэ![]() , м/с.
, м/с.
Запишем выражение, характеризующее зависимость фазовой скорости от длины волны в волноводе.
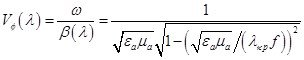
Vэ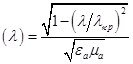
Указанные формулы были запрограммированы в математическом пакете MathCAD 14, где были построены графики зависимостей Vф и Vэ от частоты. Результаты показаны на Рис. 18.
10)Определение коэффициента затухания для заданной волны, считая, что стенки трубы выполнены из реального металла имеющего ![]() Сим/м, на основе граничных условий Леонтовича-Щукина
Сим/м, на основе граничных условий Леонтовича-Щукина
Формула для расчета коэффициента затухания на основе граничных условий Леонтовича-Щукина имеет вид:
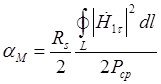 ,
,
где 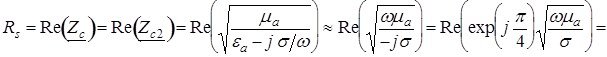
![]() - это активная часть поверхностного сопротивления волновода
- это активная часть поверхностного сопротивления волновода
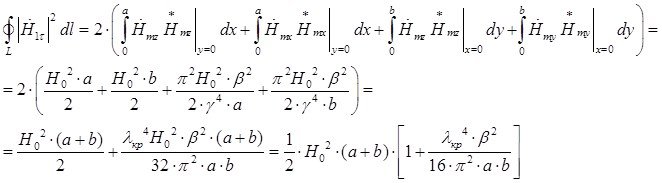
Раскроем частотную зависимость коэффициента затухания: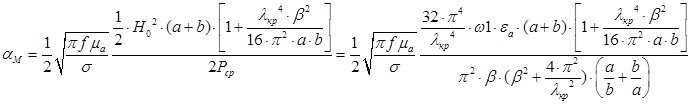
Выражение для Рср подставлено из параграфа 8 для случая, когда частота принадлежит найденному в параграфе 2 диапазону.
Сделав замену ![]() и подставив
и подставив ![]() в полученное выражение для коэффициента затухания, получим:
в полученное выражение для коэффициента затухания, получим: ![]() , Нп/м
, Нп/м
11)Расчет и построение графика зависимости коэффициента затухания волны в волноводе от частоты.
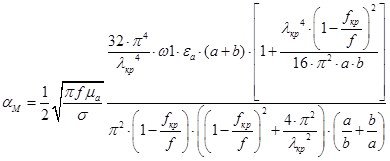 , Нп/м
, Нп/м
Указанная формула была запрограммированы в математическом пакете MathCAD 14, где был график зависимости ![]() . Результаты показаны на Рис. 19
. Результаты показаны на Рис. 19
График представлен в логарифмическом масштабе для того, чтобы показать наглядно различающиеся величины.
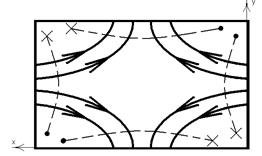
12)Определение типа волны, распространяющейся в волноводе. Изображение структуры силовых линий электрического и магнитного полей этой волны. Изображение структуры силовых линий плотности поверхностного тока проводимости, протекающего по стенкам волновода.
Данная волна является волной типа ![]() , так как только вектор
, так как только вектор ![]() имеет продольную составляющую и вдоль каждой стенки волновода укладывается одна полуволна по осям Х и У соответственно.
имеет продольную составляющую и вдоль каждой стенки волновода укладывается одна полуволна по осям Х и У соответственно.
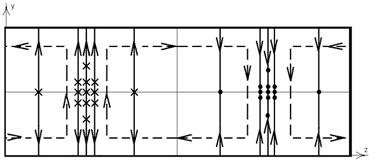
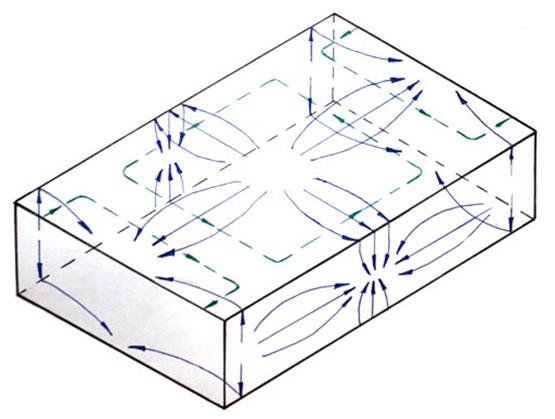
Структура силовых линий электрического и магнитного полей этой волны (Рис. 20) и плотности поверхностного тока проводимости, протекающего по стенкам волновода (Рис 21).
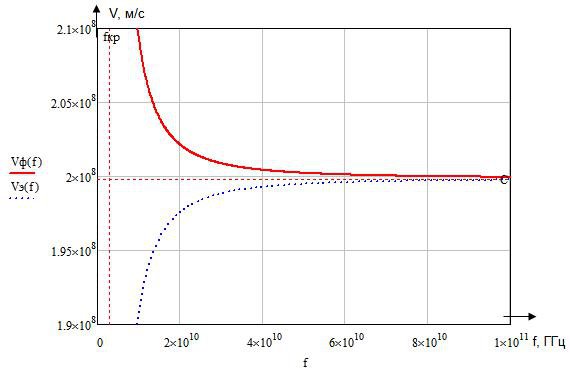 |
Рис. 18
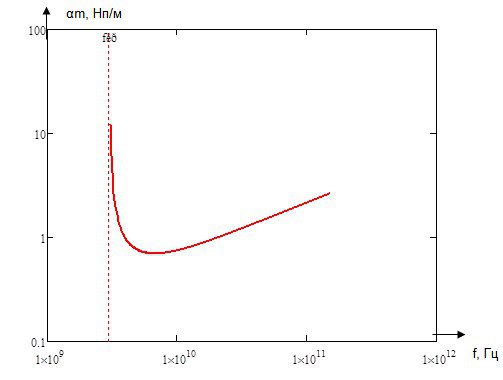 |
Рис. 19
 | ||||
 | ||||
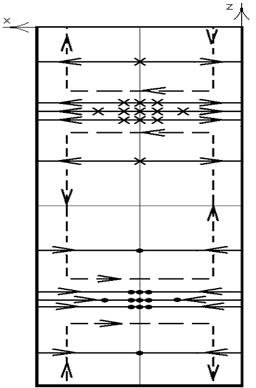 | ||||
Рис. 20
 |
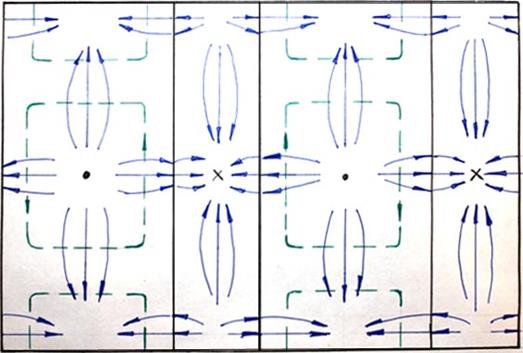 |
Рис. 21
Вывод:
Результатом работы стало исследование волны в прямоугольном волноводе. По заданным соотношениям были определены все составляющие обоих векторов электромагнитного поля. Исследованы зависимости амплитуд составляющих поля от координат в режиме бегущей волны и в режиме стоячей волны. На графиках показано экспоненциальное затухание волны с ростом координаты z в режиме стоячей волны и неизменность амплитуды ее колебаний при изменении координаты z в режиме бегущей волны (без учета потерь). В ходе исследования установлено, что рассматриваемая волна относится к типу Н11. Проверено выполнение граничных условий для касательных составляющих вектора ![]() и нормальной составляющей вектора
и нормальной составляющей вектора ![]() на стенках волновода. Получены выражения для поверхностных токов и зарядов на стенках волновода. Найден вектор Пойтинга в комплексной форме и в форме мгновенного значения. Определено среднее за период значение плотности потока энергии, проходящей через поперечное сечение волновода. Определены и рассчитаны фазовая скорость и скорость распространения энергии волны в волноводе, зависимости фазовой скорости и скорости распространения энергии построены графически. Рассчитан коэффициент затухания волны при использовании волновода из реального металла с заданной проводимостью, зависимость коэффициента затухания от частоты построена графически. Структура силовых линий электрического и магнитного полей, а также структура силовых линий плотности поверхностного тока проводимости изображены на соответствующих рисунках.
на стенках волновода. Получены выражения для поверхностных токов и зарядов на стенках волновода. Найден вектор Пойтинга в комплексной форме и в форме мгновенного значения. Определено среднее за период значение плотности потока энергии, проходящей через поперечное сечение волновода. Определены и рассчитаны фазовая скорость и скорость распространения энергии волны в волноводе, зависимости фазовой скорости и скорости распространения энергии построены графически. Рассчитан коэффициент затухания волны при использовании волновода из реального металла с заданной проводимостью, зависимость коэффициента затухания от частоты построена графически. Структура силовых линий электрического и магнитного полей, а также структура силовых линий плотности поверхностного тока проводимости изображены на соответствующих рисунках.
Математические расчёты совпадают с построенными графическими зависимостями
Использованная литература:
[1]-Техническая электродинамика / Пименов Ю.В., Вольман В.И., Муравцов А.Д. Под ред. Ю.В. Пименова: Учебное пособие для вузов. – М.: Радио и связь, 2002.
[2]-Электромагнитные волны/ Вайнштейн. Л. А. – М.: Радио и связь, 1988.
[3]-Конспект лекций за 2015 год.
Похожие материалы
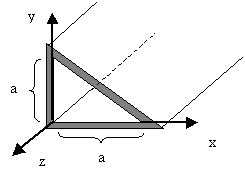
... разделения переменных при решении краевой задачи для двухмерного уравнения Гельмгольца. Наглядным примером реализации преимуществ обобщенного метода Фурье (ОМФ) [1] перед классическим при решении прикладных задач электродинамики является задача полого волновода треугольного сечения (рис.1), оболочка которого принимается за идеально проводящую, а внутренняя среда является однородной. Такая модель ...
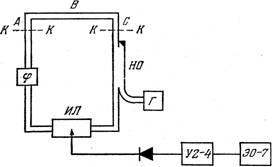
... , хотя изучение поведения бегущих волн в замкнутых системах представляет и чисто практический интерес. В настоящей работе проведено экспериментальное исследование поведения бегущих электромагнитных волн в волноводном тракте. Целью настоящей работы являлось исследование частотной зависимости амплитуды бегущей электромагнитной волны в кольцевом волноводном тракте. Для этого необходимо было решить ...
... калькуляции представлены в табл.4.2. Ленточный график работ 5. Безопасность жизнедеятельности и охрана труда Дипломная работа посвящена анализу погрешностей волоконно-оптического гироскопа. В ходе ее выполнения были проведены необходимые расчеты и сделаны выводы, которые могут послужить материалом для ...
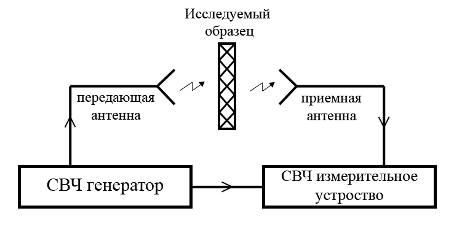
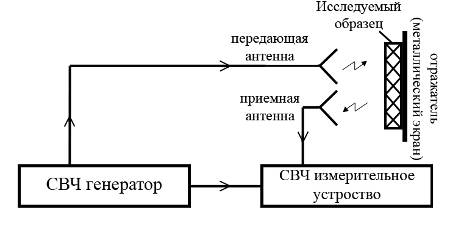
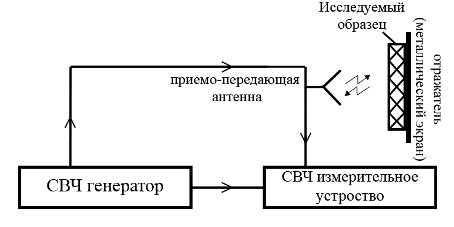
... ; 12+φг)+ 2|S11Г0|cos(φ2+2φ12+2φг+ φ11)], (5.6) а условием баланса будет: (5.7) 6 РАЗРАБОТКА И ОПИСАНИЕ СТРУКТУРНОЙ СХЕМЫ УСТРОЙСТВА РВК На рисунке 6.1 представлена структурная схема устройства, предназначенного для контроля электрической толщины радиопрозрачных диэлектрических стенок методом свободного пространства на отражение с использованием модулирующего ...
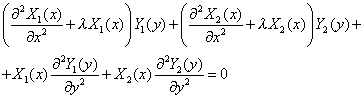
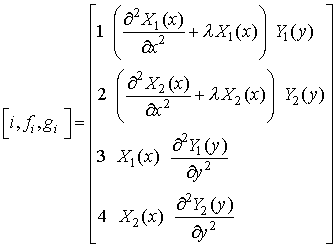
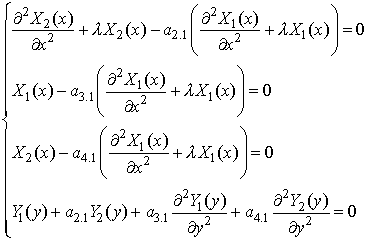
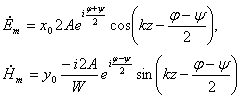


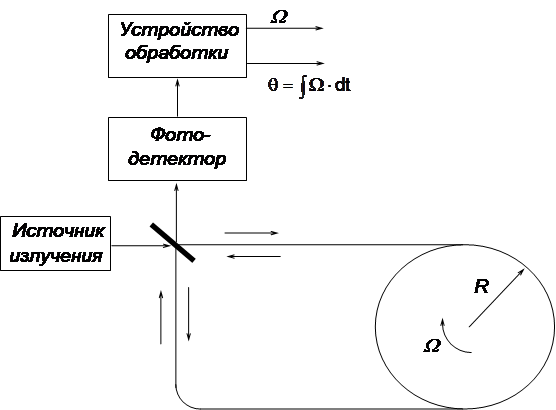
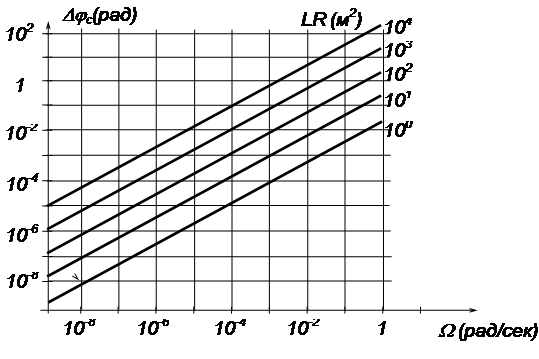

0 комментариев