Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
|
| Московский государственный технический университет (МГТУ им. Н.Э. Баумана) |
ФАКУЛЬТЕТ «РАДИОЭЛЕКТРОНИКА И ЛАЗЕРНАЯ ТЕХНИКА» (РЛ)
КАФЕДРА «РАДИОЭЛЕКТРОННЫЕ СИСТЕМЫ И УСТРОЙСТВА» (РЛ-1)
РАСЧЕТНО-ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
ПО КУРСОВОЙ РАБОТЕ
ПРИМЕНЕНИЕ АДАПТИВНОЙ ЦИФРОВОЙ ФИЛЬТРАЦИИ КАЛМАНОВСКОГО ТИПА В БЛОКЕ ИНЕРЦИАЛЬНОЙ НАВИГАЦИОННОЙ СИСТЕМЫ.
Исполнитель проекта ____________ ______________
(Подпись, дата) (И.О. Фамилия)
Группа Вариант
Руководитель проекта ____________ ______________
(Подпись, дата) (И.О. Фамилия)
Нормок
онтролер ____________ ______________
Москва. 2015
СОДЕРЖАНИЕ
ОПЕРЕДЕЛЕНИЯ, ОБОЗНАЧЕНИЯ И СОКРАЩЕНИЯ.. 3
ВВЕДЕНИЕ.. 4
1 Оптимальный фильтр Калмана. 4
1.1 Метод наименьших квадратов………………………………….......4
1.2 Метод минимизации среднеквадратичной ошибки. 5
1.3 Алгоритм фильтра Калмана. 9
2 Блок БИНС..............................................................................................12
2.1 UART.. 13
2.2 SPI 16
Результаты проделанной работы.. 18
Заключение. 19
Список литературы.. 20
ОПЕРЕДЕЛЕНИЯ, ОБОЗНАЧЕНИЯ И СОКРАЩЕНИЯ
| ЕСКД | – | система конструкторской документации |
| КД | – | конструкторская документация |
| НИИ РЭТ | – | научно-исследовательский институт радиоэлектронной техники |
| ПОС | – | припой оловянно-свинцовый |
| РКД | – | расчетно-конструкторская документация |
| РЛС | – | радиолокационная станция |
| САПР | – | система автоматического проектирования |
| СБ | – | сборочный чертеж |
| ТЗ | – | техническое задание |
| ФАР | – | фазированная антенная решетка |
| ЭКД | – | эскизно-конструкторская документация |
ВВЕДЕНИЕ
Основным отличием оптимальной фильтрации по методу Р. Калмана, т.е. фильтрации, обеспечивающей минимум средней квадратической ошибки оценки некоторой физической величины, от других способов фильтрации является рассмотрение всех случайных процессов в виде дифференциальных уравнений. В 1960 году Калман и Бьюси показали, что при случайных воздействиях оптимальный фильтр Калмана – Бьюси должен удовлетворять некоторой системе неоднородных линейных дифференциальных уравнений, по которым оказалось намного проще определить оптимальный фильтр, чем по интегральным уравнениям Винера – Хопфа, особенно в случае нестационарных случайных процессов.
Метод Калмана заключается в нахождении ожидаемого значения физической величины путем решения системы дифференциальных уравнений при начальных условиях, равных оценке величины в предыдущий момент времени. Новая оценка физической величины вычисляется как сумма ожидаемого и измеренного значений величины с учетом специального весового коэффициента, зависящего от характеристик случайных ошибок измерений, связи измеренных значений величины с истинными и степени линейной зависимости истинных значений величины в различные моменты времени.
1. ОПТИМАЛЬНЫЙ ФИЛЬТР КАЛМАНА.
1.1 Метод наименьших квадратов.
Пусть дана линейная алгебраическая система уравнений, в которой число уравнений превосходит число неизвестных:
![]()
x - n – мерный неизвестный вектор, z – известный r- мерный вектор измерений, причем r > n. Матрица D размера r*n состоит из известных элементов.
Для сглаживания находящихся в z неточностей оценка ![]() вектора
вектора ![]() должна определяться таким образом, чтобы вектор ошибок:
должна определяться таким образом, чтобы вектор ошибок:
![]() стал по возможности наименьшим. В качестве меры для величины
стал по возможности наименьшим. В качестве меры для величины ![]() выбирается евклидова норма
выбирается евклидова норма ![]() . Ее квадрат равен сумме квадратов ошибок:
. Ее квадрат равен сумме квадратов ошибок: ![]() .
.
Это выражение должно достигать минимума. Условие этого такого, что все частные производные этого выражения по ![]() должны равняться нулю:
должны равняться нулю:
![]()
![]()
![]()
![]()
![]() (1)
(1)
1.2Метод минимизации среднеквадратичной ошибки.
Пусть дана линейная система r алгебраических уравнений с n неизвестными. Число уравнений может быть больше, меньше или равно числу неизвесстных. Каждое уравнение сожеджит аддитивные ошибки изменений. В векторно- матричной форме система уравнений имеет вид:
![]()
Здесь x – вектор n искомых неизвестных. Z - вектор r заданных измерений. Матрица D размером r*n известна. Компоненты r – мерного вектора s представляют собой неизвестные ошибки измерений. Векторы x и s такие что:
![]()
![]()
![]()
Будем использовать уравнение для гаусовской оценки (1):
![]() (2)
(2)
Вычислим математическое ожидание от обеих частей:
![]()
Ошибка оценивания определяется как разность между оценкой и истинным значением:
![]()
Подставим в уравнение (2) и получим:
![]()
При условии, что математическое ожидание ошибки измерений равно нуля, найдем матрицу ковариаций ошибки измерений:
![]()
В частном случае, когда S = I, уравнение упрощается и принимает вид:
![]()
Далее сделаем предположение что оценка физической величины линейно зависит от измерения этой величины, оценка является не смещенной и что дисперсия оценки физической величины минимальна.
Математически это можно представить следующим матричным уравнением:
![]() (3)
(3)
G ( n*r мерная матрица) и g ( n – мерный вектор) подлежат определению. Несмещенность оценки требует чтобы:
![]()
Но, так как ![]() , то
, то ![]() . В связи с этим уравнение (3) упрощается:
. В связи с этим уравнение (3) упрощается:
![]()
Матрица G вычисляется исходя из требования о несмещенности оценки физической величины. Другими словами требуется обеспечить минимум дисперсии для каждого элемента вектора ![]() . Из уравнения выше становится очевидно, что каждому элементу
. Из уравнения выше становится очевидно, что каждому элементу ![]() соответствует строка матрицы g -
соответствует строка матрицы g - ![]() в виде:
в виде:
![]()
![]()
![]()
Необходимое условие минимума дисперсии оценки достигается когда все частные производные выражения выше по ![]() равны нулю:
равны нулю:
![]()
![]() (4)
(4)
Для того чтобы соотношение (4) выполнялось, необходимо чтобы дисперсия каждой отдельной ошибки измерений ![]() была минимальна. Достаточным условием этого является положительная определенность матрицы вторых производных функции
была минимальна. Достаточным условием этого является положительная определенность матрицы вторых производных функции ![]() относительно
относительно ![]() . Другими словами матрица Гесса относительно
. Другими словами матрица Гесса относительно ![]() при всех возможных i должна быть положительно определена:
при всех возможных i должна быть положительно определена:
![]()
Это условие выполняется если ![]()
Так как в реальных системах дисперсия измерений одной и той же величины всегда отлично от нуля, то это условие автоматически выполняется и соотношение (4) выполняется всегда.
Перепишем его в виде:
![]()
Это значит, что ошибки измерений и измерения линейно независимы между собой. Ошибки измерения и оценки физических величин являются так же линейно независимыми. С учетом этого:
![]()
![]() (5)
(5)
Чтобы окончательно определить G нужно найти ![]()
![]()
![]()
Подставим эти выражения в (4):
![]()
![]()
Получается, что (3) и (5) можно преобразовать в:
![]()
![]()
Т.к ![]()
![]() (6)
(6)
![]()
![]()
![]()
Подствим уравнение (6) в уравнение выше и сократим на D слева:
![]()
Т.к ![]()
![]()
![]()
![]()
Предположим теперь, что ![]() . Это значит что дисперсии всех неизвестных элементов вектора
. Это значит что дисперсии всех неизвестных элементов вектора ![]() неограниченно возрастают. Другими словами мы не имеем никакой информации о величинах
неограниченно возрастают. Другими словами мы не имеем никакой информации о величинах ![]() .
.
![]()
Тогда:
![]() (7)
(7)
![]() (8)
(8)
1.3 Алгоритм фильтра Калмана.
Пусть математическая модель рассматриваемой системы измерения имеет вид:
![]() (9)
(9)
![]() (10)
(10)
Здесь ![]() – это k –й вектор истинных значений физической величины размерностью n,
– это k –й вектор истинных значений физической величины размерностью n,![]() – k –й вектор измерений величины размерностью m,
– k –й вектор измерений величины размерностью m, ![]() –k – й вектор ошибок системы размерностью n,
–k – й вектор ошибок системы размерностью n, ![]() – k-ый вектор ошибок измерений размерностью m. Матрицы А и С представляют собой известные матрицы соответствующей размерности.
– k-ый вектор ошибок измерений размерностью m. Матрицы А и С представляют собой известные матрицы соответствующей размерности.
Требуется построить линейную несмещенную оценку величины ![]() по имеющейся последовательности результатов измерений
по имеющейся последовательности результатов измерений ![]()
Эта оценка обозначается ![]() и по определению удовлетворяет уравнению:
и по определению удовлетворяет уравнению:
![]() (11)
(11)
![]() -k-ый вектор ошибок измерений, который в случае несмещенной оценки можно характеризовать:
-k-ый вектор ошибок измерений, который в случае несмещенной оценки можно характеризовать:
![]()
На первом этапе фильтрации требуется провести предсказание (экстраполяцию) физической величины исходя из оценки этой величины в предыдущий момент времени.
![]() (12)
(12)
Подставим (9) и (10) в это уравнение:
![]() . (13)
. (13)
Последние 2 члена справа, очевидно, характеризуют ошибки экстраполяции. Для этих ошибок можно найти матрицу ковариаций:
![]()
Имея в виду, что величины ![]() и
и ![]() некоррелированы, получим:
некоррелированы, получим:
![]() (14)
(14)
![]() матрица ковариаций вектора ошибок системы измерений.
матрица ковариаций вектора ошибок системы измерений.
Теперь для построения оптимальной оценки мы имеем 2 уравнения: уравнение для вектора измерений (10) и уравнение для экстраполяции (13). Запишем их в систему уравнений:
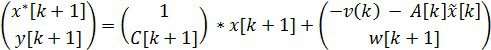
Или
![]()
Найдем матрицу ковариации вектора ![]()
![]()
Верхний правый и нижний левый коэффициенты равны нулю, потому что величины ![]() и
и ![]() , а так же
, а так же ![]() и
и ![]() некоррелируют.
некоррелируют.
Далее будем использовать результаты расчета гауссовско-марковской оценки, полученные в предыдущем пункте. Согласно уравнению (7):
![]() (15)
(15)
![]()
![]()
![]()
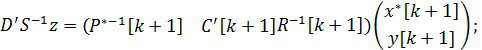
Подставим последнее выражение в (15):
![]()
![]()
Обозначим ![]() как
как ![]() . (16)
. (16)
Эта матрица называется калмановским усилением.
Затем используем формулу для ![]() :
:
![]()
![]()
![]()
![]() (17)
(17)
Запишем промежуточный результат с учетом (16) и (17):
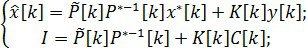
Решим эту систему относительно ![]() и получим:
и получим:
![]() (18)
(18)
Умножим второе уравнение системы на ![]() справа, на
справа, на ![]() справа решим относительно
справа решим относительно ![]() :
:
![]() (19)
(19)
В результате с помощью уравнений (12) , (14) , (17) , (18) , (19) можно составить алгоритм Калмана:
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
Начальные условия определяются следующим образом. В начальный момент времени ![]() производится первое измерение
производится первое измерение ![]() . Для начала работы фильтров необходимо сначала промести не менее n измерений. После этого строится первая оценка
. Для начала работы фильтров необходимо сначала промести не менее n измерений. После этого строится первая оценка ![]() и определяется значение матрицы
и определяется значение матрицы![]() . Априорные сведенья в начальный момент времени: равенство нуля математического ожидания величины
. Априорные сведенья в начальный момент времени: равенство нуля математического ожидания величины ![]() и бесконечная дисперсия
и бесконечная дисперсия ![]()
2 Блок БИНС
Блок БИНС - это система, обеспечивающая навигацию и ориентацию устройства в пространстве. Выполнение этих функций обеспечивается двумя основными компонентами блока: трехосевым акселерометром ADIS16210 и магнитным компасом HMR3500.
ADIS16210 - это цифровой акселерометр, который обеспечивает точные измерения по углам крена и тангажа в диапазоне ±180°. Он сочетает в себе три осевых датчика ускорения с обработкой сигналов, адресуемые пользователем регистры для сбора данных или программирования и SPI интерфейс. Кроме того, устройство включает в себя блок специальной калибровки для обеспечения оптимальной точности измерений. Он также имеет цифровой температурный датчик и блок измерения напряжения питания. Устройство имеет возможность внутренней настройки для калибровки системы, управлением частотой дискретизации, фильтрацией, конфигурацией входов/выводов устройства и питания.
HMR3500 - это трехосевой цифровой магнитный компас с подстраиваемой системой координат. Он так же содержит встроенный трехосевой акселерометр, датчик температуры, а так же микроконтроллер со встроенным цифро-аналоговым преобразователем.
Управление этими устройствами обеспечивается с помощью микроконтроллера STM32F4. Цифровой акселерометр подключен с помощью интерфейса SPI, а магнитный компас - с помощью интерфейса RS-232. В силу своих особенностей, микроконтроллер STM32F4 не имеет встроенного модуля RS-232, поэтому взаимодействие с компасом обеспечивается по средством микросхемы преобразования интерфейсов MAX3313EEUB, подключенной к модулю UART микроконтроллера.
Взаимодействие с внешними устройствами производится по интерфейсу передачи данных RS-485. Для преобразования интерфейса UART в RS-485 используется микросхема ADM2582, которая обеспечивает изоляцию входного и выходного сигналов, а так же изоляцию по питанию. Микросхема позволяет передавать данные с максимальной пропускной способностью 15 Мбит/сек.
2.1 UART
UART - это асинхронный последовательный интерфейс передачи данных, использующий для приема и передачи всего 2 сигнальные линии.
При передаче по интерфейсу UART каждому байту данных предшествует СТАРТ-бит, сигнализирующий приемнику о начале посылки, за СТАРТ-битом следуют биты данных. Завершает посылку СТОП-бит, гарантирующий паузу между посылками. СТАРТ-бит следующего байта посылается в любой момент после СТОП-бита, то есть между передачами возможны паузы произвольной длительности. СТАРТ-бит, обеспечивает простой механизм синхронизации приемника по сигналу от передатчика. Внутренний генератор синхроимпульсов приемника использует счетчик-делитель опорной частоты, обнуляемый в момент приема начала СТАРТ-бита. Этот счетчик генерирует внутренние стробы, по которым приемник фиксирует последующие принимаемые биты.
Существует общепринятый ряд стандартных скоростей: 300; 600; 1200; 2400; 4800; 9600; 19200; 38400; 57600; 115200; 230400; 460800; 921600 бод. Если скорость передатчика и приемника не будут совпадать, то передачи может не быть вообще, либо будут считаны не те данные.
Формат кадра по интерфейсу UART представлен на рисунке 1.

Рисунок 1- Формат кадра интерфейса UART
В этом протоколе логический нуль лежит от +3 до +12 вольт, а единица от -3 до -12, соответственно. Промежуток от -3 до +3 вольт считается зоной неопределенности.
Структурная схема модуля UART в контроллере STM32F4 представлена на рисунке 2.
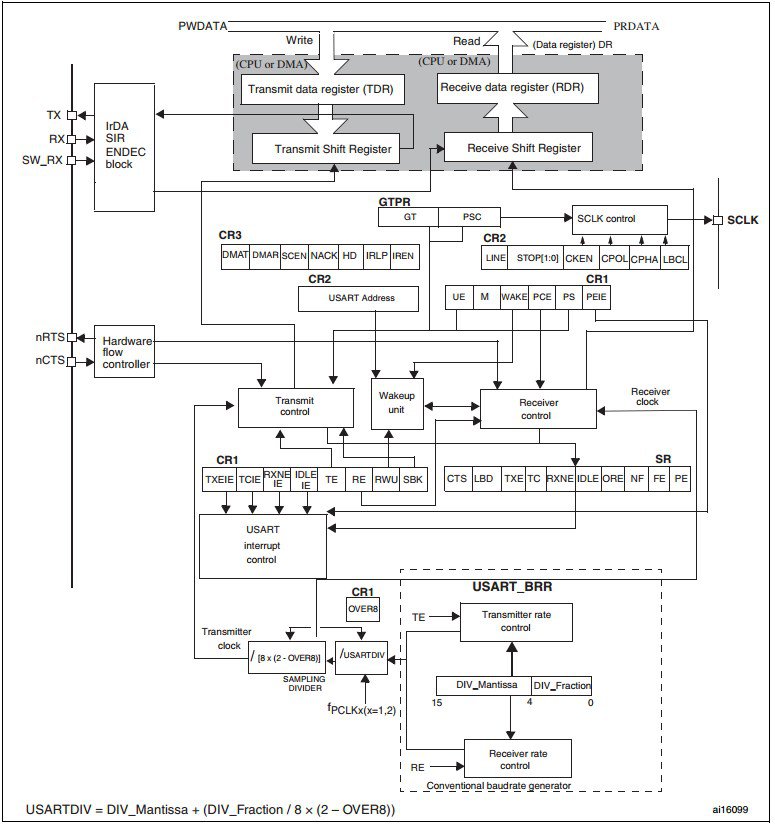
Рисунок 2 - Устройство UART
2.2 SPI
SPI – это последовательный интерфейс передачи данных между одним ведущим и несколькими ведомыми. В SPI используются четыре цифровых сигнала:
MOSI — выход ведущего, вход ведомого (англ.Master Out Slave In). Служит для передачи данных от ведущего устройства ведомому. MISO — вход ведущего, выход ведомого (англ.Master In Slave Out). Служит для передачи данных от ведомого устройства ведущему. SCLK — последовательный тактовый сигнал (англ.Serial Clock). Служит для передачи тактового сигнала для ведомых устройств. CS или SS — выбор микросхемы, выбор ведомого (англ.Chip Select, Slave Select).Непосредственно для обмена используется две однонаправленных линии данных (одна от ведущего к ведомому, вторая – наоборот) и одна линия тактового сигнала, формируемая ведущим.
 В простейшем случае к ведущему устройству подключено единственное ведомое устройство и необходим двусторонний обмен данными. В таком случае используется трехпроводная схема подключения. Интерфейс SPI позволяет подключать к одному ведущему устройству несколько ведомых устройств, причем подключение может быть осуществлено несколькими способами.
В простейшем случае к ведущему устройству подключено единственное ведомое устройство и необходим двусторонний обмен данными. В таком случае используется трехпроводная схема подключения. Интерфейс SPI позволяет подключать к одному ведущему устройству несколько ведомых устройств, причем подключение может быть осуществлено несколькими способами.
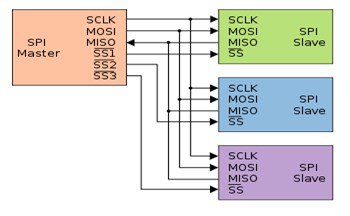
Рисунок 3- Радиальная структура связи с несколькими ведомыми устройствами через SPI
Первый способ позволяет реализовать радиальную структуру связи (топология типа «звезда»), его принято считать основным способом подключения нескольких ведомых устройств (рисунок 3). В данном случае для обмена более чем с одним ведомым устройством ведущее устройство должно формировать соответствующее количество сигналов выбора ведомого устройства (SS). При обмене данными с ведомым устройством, соответствующий ему сигнал SS переводится в активное (низкое) состояние, при этом все остальные сигналы SS находятся в неактивном (высоком) состоянии. Выводы данных MISO ведомых устройств соединены параллельно, при этом они находятся в неактивном состоянии, а перед началом обмена один из выходов (выбранного ведомого устройства) переходит в активный режим.
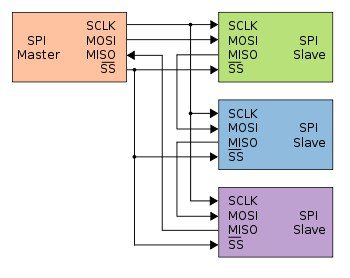
Рисунок 4- Кольцевая структура связи с несколькими ведомыми устройствами через SPI
Второй способ позволяет реализовать структуру связи типа «кольцо». В данном случае для активации одновременно нескольких ведомых устройств используется один сигнал SS, а выводы данных всех устройств соединены последовательно и образуют замкнутую цепь (рисунок 4). При передаче пакета от ведущего устройства этот пакет получает первое ведомое устройство, которое, в свою очередь, транслирует свой пакет следующему ведомому устройству и так далее. Для того, чтобы пакет от ведущего устройства достиг определенного ведомого устройства, ведущее устройство должно отправить еще несколько пакетов.
В зависимости от полярности линии тактового сигнала существует 4 возможных режима работы интерфейса (рисунок 5).
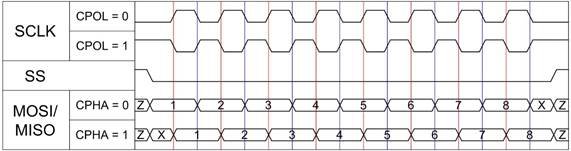
Рисунок 5- Режимы работы интерфейса SPI
Результаты проделанной работы
В результате проделанной работы были разработаны конструкторские документы на блок БИНС: спецификация, перечень элементов, схема электрическая принципиальная и сборочный чертеж. Так же была модернизирована конструкция корпуса блока, представленная на рисунке 6. 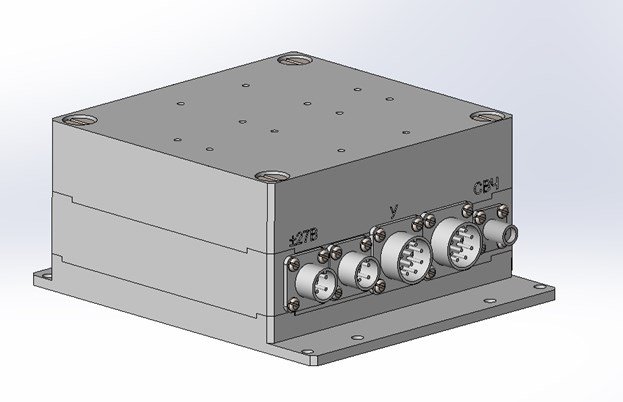
Рисунок 6 - Блок БИНС
Было разработано программное обеспечение, для приема информации об углах тангажа, рыскания и крена с блока БИНС, ее адаптивной фильтрации и вывода результатов на экран в удобной для пользователя форме. Результаты представлены в приложении 1.
Заключение
В курсовой работе был разработан корпус блока инерциальной навигационной системы БИНС, разработана конструкторская документация в составе: схема электрическая принципиальная, сборочный чертеж, перечень элементов и спецификация. Были изучены основные электронные устройства, входящие в блок БИНС, и интерфейсы передачи данных между ними. Было разработано программное обеспечение, позволяющее производить прием данных с блока, их адаптивную цифровую фильтрацию и выводить результаты в наглядной для пользователя форме.
Список литературы
1. Павлова Н.И., Абрамов В.П., Безжовчий О.А., Кутеко А.М., Методические указания к выполнению курсового проекта по дисциплине «Конструирование и технология производства РЭС» и производственно-технологической практике. М.: Издательство МГТУ им. Н.Э.Баумана, 2014
2. Парфенов Е.М., Камышная Э.Н., Усачов В.П. Проектирование конструкций радиоэлектронной аппаратуры: Учебное пособие для вузов. М.: Радио и связь, 1982. 272 с.
3. Разработка и оформление конструкторской документации РЭА: Справочное пособие / Э.Т.Романычева, А.К.Иванова, А.С.Куликов, Т.П.Новикова. М.: Радио и связь, 1984, 256 с.
Похожие материалы
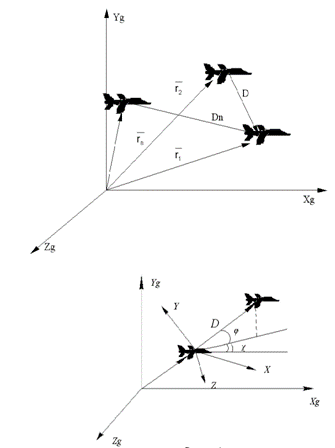
... алгоритмов обработки информации СМСН с целью определения параметров движения ведущего ЛА и относительного движения. В этом случае нетрудно реализовать алгоритмы СМСН БЛА. Задачу обработки информации относительного движения рассматривали при полном составе измерений: углах визирования, угловой скорости линии визирования, дальности и скорости изменения дальности. Ключевым вопросом при решении этой ...

0 комментариев