Использование пакета Microsoft Excel для работы с логическими функциями

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра вычислительной техники

отчет

по лабораторной работе №5

по дисциплине «Информатика»

Тема: «Использование пакета MicrosoftExcel
для работы с логическими функциями»

Студент гр. 5891		Агеев К.А.
Ассистент каф. ВТ		Бондаренко П.Н.

Санкт-Петербург, 2015

Содержание:

1 Цель работы.. 3

2 Основные теоретические положения. 3

3 Экспериментальные результаты. 3

3.1. Построение таблицы истинности заданной функции. 3

3.2Преобразование заданной функции. 5

3.3 Построение таблицы для упрощенной функции. 6

3.3 Сравнение таблиц истинности. 6

3.4 Представление функции в форме СДНФ. 6

3.5 Упрощение формы СДНФ. 7

4 Заключение. 8

1 Цель работы

Освоить основные приемы работы с логическими функциями пакета MS Excel, практически освоить изученные теоретические основы алгебры логики.

Для функции, заданной в виде аналитического выражения построить таблицу истинности. Представить функцию в форме СДНФ, упростить полученную СДНФ функции, построить таблицу истинности для упрощенного выражения. Сравнить полученные результаты.

Заданная функция .

2 Основные теоретические положения.

Для работы со сложными формулами в Excel реализован Мастер функций, хотя формулу можно вводить и непосредственно с клавиатуры. При конструировании формулы с помощью Мастера функций в диалоговом окне отображается имя функции, все ее аргументы, описание функции и каждого аргумента, текущий результат функции и всей формулы.

Функции и выражения могут быть вложены друг в друга, что позволяет конструировать проверку достаточно сложных условий.

В Excel имеются следующие логические функции: ЕСЛИ, И, ИЛИ, ИСТИНА, ЛОЖЬ, НЕ.

Описание каждой функции можно найти в Мастере функций.

3 Экспериментальные результаты.

3.1. Построение таблицы истинности заданной функции.

Таблица строится с использованием логических функций.

B, C ,D – столбцы аргументов функции.

Для упрощения построения таблицы и визуального восприятия ввел дополнительные переменные. Значения переменных показаны в таблице1.

0(C→DB)	H
DC↔CBC	G

Таблица 1 – Значение промежуточных переменных.

B	C	D	DC	DB	H	DCH	0G	(DCH)B0G	F
0	0	0	0	0	0	0	0	0	1
0	0	1	0	0	0	0	0	0	1
0	1	0	0	0	1	1	1	1	0
0	1	1	1	0	1	1	0	0	1
1	0	0	0	0	0	0	0	0	1
1	0	1	0	1	0	0	0	0	1
1	1	0	0	0	1	1	1	1	1
1	1	1	1	1	0	1	0	1	1

Таблица2 – Таблица истинности, с промежуточными результатами.

Столбец DCреализует функцию И, используя в качестве аргументов ячейки столбцов Dи C. Для строки4 формула выглядит следующим образомf(x)=И(D4;C4).

Столбец DBреализует функцию И, используя в качестве аргументов ячейки столбцов D иB. Для строки 4 формула выглядит следующим образомf(x)=И(D4;C4).

Столбец Hсодержитзначение0(C→DB), как показано в таблице 1. И реализует функцию инверсии, импликации аргументов ячеек столбцовCи DB.Функции импликации нет в списке логических функций, реализуемых в Excel, поэтому эту функцию реализовал с использованием функции ЕСЛИ.Для строки 4 формула выглядит следующим образом f(x)=НЕ(ЕСЛИ(И(C4=1;F4=ЛОЖЬ);ЛОЖЬ;ИСТИНА)).

Столбец DCH реализует функцию ИЛИ, используя в качестве аргументов ячейки столбцов DCи H. Для строки 4 формула выглядит следующим образом f(x)=ИЛИ(E4;G4).

Столбец 0G содержит инверсию значения DC↔CBC, как показано в таблице 1.Реализует функцию инверсии, эквивалентности столбца аргументов DC и результата функции И столбцов аргументов С и ВС.Функции эквивалентности также нет в списке логических функций, реализуемых в Excel, поэтому эту функцию необходимо реализовать с использованием функции ЕСЛИ. Для 4 строки формула выглядит следующим образом f(x)=НЕ(ЕСЛИ(И(D4;C4)=ИЛИ(C4;И(B4;C4));ИСТИНА;ЛОЖЬ)).

Столбец (DCH)B0G реализует функцию И, использую значения аргументов ячейки столбцов DCH и B. Также, по полученному результату, реализует функцию ИЛИ, используя в качестве аргументов полученный результат предыдущей функции и значенияаргументов ячеек столбца B.

Последний столбец таблицы F соответствует реализации функции импликации, используя в качестве аргументов ячейки столбцов (DCH)B0G и В. Для строки 4 формула выглядит следующим образом f(x)=ЕСЛИ(И(J4=ИСТИНА;B3=0);ЛОЖЬ;ИСТИНА)

Дополнительно результат может быть представлен в более удобной для анализа форме с использованием двоичного алфавита (дополнительный столбец F) с использованием формулы f(x)=ЕСЛИ(K4=ИСТИНА;1;0).

Результат построения таблицы истинности показан на рисунке 1.

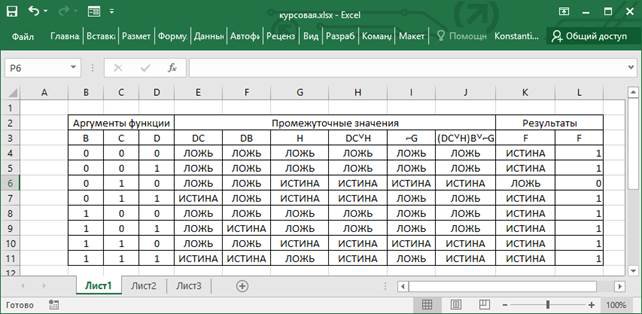
Рисунок 1 – Таблица истинности функции

3.2Преобразование заданной функции.

Для упрощения преобразования я разделил всю процедуру на 3 этапа.

Этап 1. Преобразование первой части функции (DC 0(C→DB))B. Следуя правилу замены операции импликации 0(C→DB) можно записать как 0(0CDB).По закону де Моргана 0(0C (DB))=00С0(DB)=C0(DB)=С(0D 0B). По закону дистрибутивности С(0D 0B)=C0DC0B.Получилось (DC С0DC0B)B. Вынес С за скобку по закону дистрибутивности получил(D 0D 0B)BС. Сократил

D 0D по закону исключающего третьего и получил 0BBC, сократил 0BB. Остаток С и есть результат первого этапа.

Этап 2. Преобразование второй части функции 0 (DC↔CBC).Следуя закону поглощения CBC=С. По правилу замены эквивалентности

DC↔C=(DCC) (0DC0C). Воспользовался законом идемпотентности и сократил DCC=DC, разложил 0DC по закону де Моргана и получил DC ((0D0C) 0C.По закону поглощения (0D 0C) 0C=0C, я получил DC0C. Воспользовавшись правилом свертки DC0C=0CD. Последняя операция во второй части, это разложение по закону де Моргана и преобразование по закону двойного отрицания0 (0CD)=00C0D=C0D.

Этап 3. По двум предыдущим этапам я получил общую формулу функции СC0D→B. Здесь также можно сократить по правилу сверткиСC0D =C0D. И окончательный результат преобразования получился f(x)= C0D→B.

3.3 Построение таблицы для упрощенной функции.

Для полученной функции таблица истинности построена без использования промежуточных разложений. Формула ячеек результата иметь следующий вид=ЕСЛИ(И((И(C4;НЕ(D4)))=ИСТИНА;B4=0);ЛОЖЬ;ИСТИНА).

3.3 Сравнение таблиц истинности.

Сравнение таблиц истинности выполняется с использованием функций Excel.

Формула для определения выглядит следующим образом:

=ЕСЛИ(И(L4=O4;L5=O5;L6=O6;L7=O7;L8=O8;L9=O9;L10=O10;L11=O11); "Разложение верно";"Разложение ошибочно")

Результат анализа показан на рисунке 2.

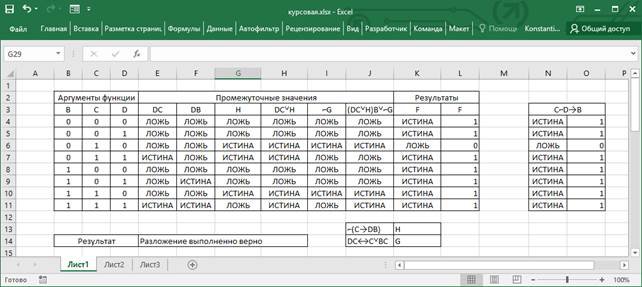
Рисунок 2 – Результат анализа разложения

3.4 Представление функции в форме СДНФ.

B	C	D	F(B,C,D)
0	0	0	1
0	0	1	1
0	1	0	0
0	1	1	1
1	0	0	1
1	0	1	1
1	1	0	1
1	1	1	1

Таблица 3 – Таблица истинности

В первой строке значения всех трех переменных равны 0. Следовательно первый член СДНФ рассматриваемой функции выглядит так : 0B0C0D

Переменные второго члена СДНФ: B=0; C=0; D=1. Второй член СДНФ равен 0B0CD.

Значение функции третьей строки равно 0. Поэтому третий член не записывается.

Переменные четвертого члена СДНФ: B=0; C=1; C=1.Четвертый член СДНФ равен 0BCD.

Переменные пятого члена СДНФ: B=1; C=0; D=0. Пятый член СДНФ равен B0C0D.

Переменные шестого члена СДНФ: B=1; C=0; D=1.Шестой член СДНФ равен B0CD.

Переменные седьмого члена СДНФ: B=1; C=1; D=0.Седьмой член СДНФ равен BC0D.

Переменные восьмого члена СДНФ: B=1; C=1; D=1;. Восьмой член СДНФ равен BCD.

Результат представления функции СДНФ:

F(B,C,D)= (0B0C0D) (0B0CD) (0BCD) (B0C0D) (B0CD) (BC0D) (BCD)

3.5 Упрощение формы СДНФ.

Для упрощения СДНФ формы я использовал законы алгебры логики:

- Закон поглощения A AB = A;

- Правило склеивания AB A0B = A;

- Правило свертки A 0AB = A B, 0A AB = 0A B;

- Законы де Моргана 0 (AB)= 0A 0B, 0 (A B) = 0A0B

F(B,C,D)= (0B0C0D) (0B0CD) (0BCD) (B0C0D) (B0CD) (BC0D) (BCD) =

(0B0C) (0BCD) (B0C) (B0C) (BC) =

(0B0C) (B0C) (0BCD) (BC) =

0C (0BCD) (BC) =

0C (0BD) (BC) =

(0BD) 0C B =

B 0C D.

Для проверки полученной упрощенной формы СДНФ построил таблицу истинности и сравнил с исходной таблицей. Результат таблицы истинности для полученной формы показан на рисунке 3.

Для сравнения полученной и исходной таблицы использовал формулу =ЕСЛИ(И(G5=L5;G6=L6;G7=L7;G8=L8;G9=L9;G10=L10;G11=L11;G12=L12); "Разложение верно";"Разложение ошибочно"). Результат сравнения показан на рисунке 4.

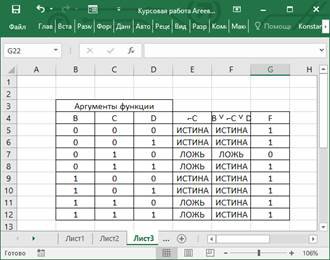
Рисунок 3 – Таблица истинности для упрощенной формы СДНФ

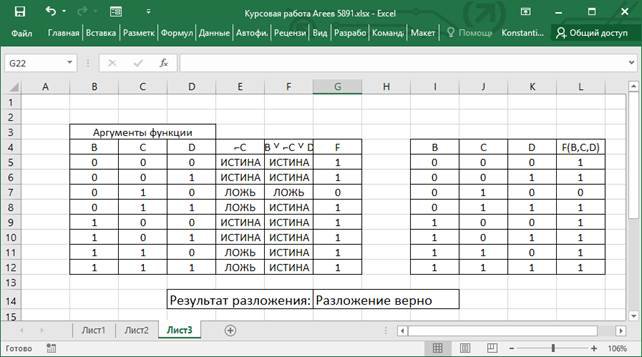
Рисунок 4 – Результат сравнения полученной таблицы

4 Заключение

В процессе работы освоил основные приемы работы с логическими функциями пакета MS Excel, освоил на практике изученные теоретические основы алгебры логики.

Для функции, заданной в виде аналитического выражения построил таблицу истинности. Представил функцию в форме СДНФ, упростил полученную СДНФ функцию, построил таблицу истинности для упрощенного выражения. Сравнил полученные результаты.