ВСТУП
Дисципліна “Основи систем автоматизованого проектування” є однією з основних спеціальних дисциплін, яку вивчають студенти в сьомому та восьмому семестрах.
Метою лабораторного практикуму є ознайомлення студентів спеціальності «Промислове та цивільне будівництво» з основами роботи в математичному пакеті MathCAD, а також застосування MathCAD при розв’язанні важливих інженерних задач.
До виконання лабораторних робіт допускаються студенти, які прослухали лекції з відповідних розділів дисципліни “Основи систем автоматизованого проектування”. Перед виконанням кожної лабораторної роботи слід уважно ознайомитись з теоретичною частиною роботи.
У даному практикумі зібрано всі лабораторні роботи та індивідуальні завдання для кожної з них, які студент має виконати під час вивчення першого та другого модулів.
Кожну лабораторну роботу виконує група студентів, а кожне індивідуальне завдання окремо кожний студент. Після виконання кожного завдання слід робити висновок.
Після кожного протоколу наведено питання для допуску й захисту лабораторної роботи. Лабораторний практикум закінчується питаннями для модульного контролю.
МОДУЛЬ 1. Місце САПР в проектуванні будівель та споруд
лабораторна робота № 1
Знайомство з інтерфейсом програми MathCAD. Виконання найпростіших розрахунків та операцій в MathCAD
Література до теми: [1-4].
Мета роботи:
1. Ознайомитись з інтерфейсом Mathcad та його організацією.
2. Навчитися вводити та обчислювати вирази в Mathcad.
3. Навчитися редагувати окремі вирази, об’єкти або групи об’єктів в Mathcad.
Завдання 1.1. Організація графічного інтерфейсу Mathcad.
Теоретична частина
Mathcad - це інтегроване середовище для розв’язання різноманітних математичних задач. Mathcad включає наступні функціональні компоненти:
• скоординовану та добре організовану систему меню різних рівнів вкладеності;
• набір панелей інструментів;
• текстовий редактор, що забезпечує ефективні коментарі всіх процесів математичних обчислень;
• редактор формул;
• редактор графіків, включаючи тривимірні;
• обчислювальну систему, яка полегшує виконання математичних операцій, як в чисельному, так і в аналітичному (символьному) вигляді;
• набір шаблонів, який прискорює введення вихідних даних, а також забезпечує зручну та ефективну систему введення;
• систему перевірки правильності написання математичних виразів;
• вбудовану систему виведення результатів розрахунку;
• контекстно-залежні меню Mathcad. Mathcad має ієрархічну систему меню, що складається з головного меню та системи падаючих, спливаючих та контекстно-залежних меню (підменю).
Хід роботи:
1. Завантажте систему Mathcad. Завантаження здійснюється при запуску виконуючого файлу Mathcad.ехе, розташованого в каталозі зі встановленою системою, або через меню Пуск, або через ярлик, наприклад на робочому столі.
2. Створіть новий документ Mathcad. Після запуску Mathcad автоматично завантажується файл Untitled 1 (Безіменний 1), що представляє собою шаблон Normal (звичайний) робочого документу Mathcad, що має назву Worksheet (Робочий лист). Окрім того, автоматично завантажуються вікна Tip of the day (Порада дня) та Mathcad Resource (Документація Mathcad). Перед початком роботи ці вікна необхідно закрити. У вікні Tip of the day необхідно зняти галочку Show tip at startup (Показувати пораду при запуску) та натиснути на кнопку Close.
Рис.1.1. Робоче вікно Mathcad
Головне меню. Головне меню Mathcad займає верхню строчку робочого вікна. Вигляд головного меню показаний на рис. 1.2. Натискання мишею на будь якому пункті меню відкриває підменю з переліком команд:

Рис.1.2. Головне меню Mathcad
1. Управління робочим вікном Mathcad.
2. File (Файл) – команди, пов’язані зі створенням, відкриттям, збереженням, пересилкою по електронній пошті та друком на принтері файлів з документами.
3. Edit (Правка) – команди, що відносяться до правки тексту (копіювання, вставка, видалення фрагментів тощо).
4. View (Вид) – команди, що управляють зовнішнім видом документу в робочому вікні Mathcad, а також команди створення файлів анімації.
5. Insert (Вставка) – команди вставки різних об'єктів в документ.
6. Format (Формат) – команди форматування тексту, формул та графіків.
7. Tools (Інструменти) – команди управління обчислювальним процесом.
8. Symbolics (Символьні обчислення) – команди символьних обчислень.
9. Window (Вікно) – команди, що дозволяють управляти розташуванням вікон з різними документами на екрані.
10. Help (Допомога) – команди виклику довідкової інформації.
Натискання мишею на пункті підменю викликає появу відповідного діалогового вікна.
Обравши в головному меню (рис. 1.3) Tools Þ Preferance (Інструменти Þ Налаштування), можна зробити роботу в Mathcad більш зручною.
Рис. 1.3. Вікно Preferance в Mathcad 15
Панелі інструментів. Панелі інструментів призначені для швидкого виконання команд, що найбільш часто використовуються. Вид панелей інструментів показаний на рис. 1.4.
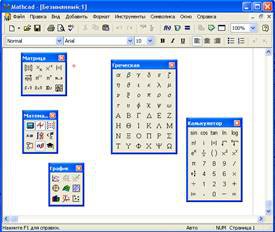
Рис. 1.4. Панелі інструментів
Ø Головне меню Mathcad здійснює повне управління всіма процесами, окрім того, дозволяє виконувати всі команди, що поєднанні в решту меню.
Ø Standard (Стандартна) служить для виконання дій з файлами, редагування документів, вставки об’єктів тощо.
Ø Formatting (Форматування) призначена для форматування тексту та формул.
Ø Math (Математика) служить для вставки математичних символів та операторів в документи.
Ø Recources (Додаткові ресурси) містить список електронних книг, що входять в оболонку Mathcad.
Ø Controls (Контроль) містить кнопки для додаткового контролю роботи MathCAD-документу.
Ø Debug (Налагодження) з’явилася в Mathcad 13, служить для трасування виконання програм.
При наведенні курсора миші на будь-яку з кнопок поруч з нею з'явдяється вспливаюча підказка – короткий текст, що пояснює призначення кнопки.
Завдання 1.2. Побудова виразів та їх обчислення.
Теоретична частина
Перед початком роботи курсор на екрані має вигляд хрестика. В момент введення виразу курсор набуває вигляду синього кутика, що обмежує вираз, що вводиться.
Ø В робочому документі введіть будь-які буквені вирази та надайте їм чисельні значення.
Ім’я виразу (все, що стоїть зліва від оператора присвоєння) може складатися з латинських, російських, грецьких та інших букв та цифр, знаків підкреслювання (_), штрихів (‘), символу відсотку (%), знаку нескінченності, що вводяться з клавіатури.
Імена змінних та функцій не можуть починатися з цифри, знаку підкреслювання, штрихів, символу відсотку, та не можуть містити пробіли. Символ нескінченності може бути тільки першим символом в імені.
Увага! Mathcad сприймає прописні та рядкові букви як різні ідентифікатори, теж саме стосується букв, що зображені різними шрифтами, - це різні імена.
Mathcad не робить різниці між іменами змінних та функцій. Якщо спочатку визначити функцію f(x), а потім – змінну f, виявиться неможливим використовувати f(x) в розрахунках будь де після визначення f.
Хід роботи:
1. Виберіть оператор привласнення (:=) на математичній панелі Calculator (Калькулятор). В подальшому оператор привласнення можна вводит из клавіатури, натиснувши клавішу Shift+«двокрапка» (:).
2. Наберіть вираз, який необхідно обчислити і натисніть клавішу (=), після цього отримаєте результат обчислень. Виконайте в робочому документі Mathcad наступні дії (див. рис. 1.5).
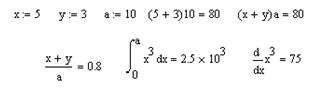
Рис. 1.5. Приклади побудови математичних виразів
Завдання 1.3. Робота з «чіпкими» операторами.
Теоретична частина
«Чіпки» оператори – це зведення в ступінь, знаходження кореня, знаменник дробу (рис. 1.6). Щоб звільнитися від «чіпкого оператора», потрібно виділити клавішею пробілу або клавішею ® (стрілка вправо) потрібну частину виразу, тоді наступна операція буде відноситися до всього виділеного виразу.

Рис. 1.6. Приклади побудови виразів з «чіпкими» операторами
Ø Потренуйтесь у введенні виразів і отриманні їх результатів (рис. 1.6, 1.7). Для зведення в ступінь використовуйте клавішу Shift+«^».
Завдання 1.4. Редагування об’єктів Mathcad.
Теоретична частина
Редагування введених об’єктів відбувається звичайним для всіх Windows-додатків способом:
1. Кутик курсору переміщується по екрану клавішами зі стрілками або натисканням лівої кнопки миші в потрібному місті екрану.
2. Для виділення кутиком курсору одного символу потрібно встановити синій кутик курсору таким чином, щоб він охоплював потрібний символ зліва або справа.
3. Для розширення виділення на частину виразу або на весь вираз цілком необхідно використовувати клавіші зі стрілками або клавішу пробілу. Для виходу з «чіпкого» оператора бажано користуватися клавішею пробілу. Кутик курсору повинен охоплювати весь вираз або всю його частину, над якою необхідно виконати будь-які дії.
4. Для виділення частини виразу або всього виразу потрібно клацнути мишею на початку або в кінці частини виразу який виділяється, та перемістити курсор до іншого кінця, не відпускаючи ліву кнопку миші. Можна використовувати комбінацію клавіш Shift+← або Shift+→.Виділена частина виразу має чорний фон. Виділення в Mathcad використовується для вирізання або копіювання частини виразу, зміни шрифту, а також для виконання символьних обчислень з частинами виразів.
5. Для виділення об’єкту або групи об’єктів (будь яких – математичних, текстових або графічних) потрібно клацнути мишею на вільному місці робочого документу та розтягнути пунктирний прямокутник виділення таким чином, щоб він охоплював потрібні вам об’єкти. Один об’єкт при цьому буде виділений синім кутиком курсору, а група об’єктів – обведена пунктирною рамочкою.
Всі три види виділення виразів показані на рис. 1.7.

Рис. 1.7. Види виділення виразів в Mathcad
Якщо необхідно видалити, вирізати або скопіювати в буфер обміну виділену частину виразу, виділений об’єкт цілком або групу виділених об’єктів, треба виконати наступні дії:
1. Для видалення натисніть клавішу Delete або Backspace.
2. Для вирізання в буфер обміну натисніть кнопку Cut (Вирізати) або Ctrl+x із зображенням ножиць на стандартній панелі Mathcad. При натисканні кнопки Cut об’єкт видаляється з робочого документу, але переноситься в буфер.
3. Для копіювання в буфер обміну натисніть кнопку Copy (Копіювати) або Ctrl+c із зображенням двох сторінок на стандартній панелі Mathcad. При натисканні кнопки Copy об’єкт залишається в робочому документі та копіюється в буфер.
4. Для вставки об’єкта з буферу обміну встановіть курсор у вигляді хрестика в те місце, куди ви хочете вставити вміст буферу обміну, та натисніть кнопку Paste (Вставити) або Ctrl+v на стандартній панелі Mathcad.
Окрім стандартних інструментів в Mathcad, як і в усіх Windows-додатках, виділений об’єкт або виділену групу об’єктів можна пересунути або скопіювати за допомогою миші. Для цього необхідно:
1. Підвести мишу до виділеного об’єкту або групі об’єктів, щоб з’явся значок у вигляді чорної долоні.
2. Натиснути ліву кнопку миші і перемістити курсор в те місце, куди треба пересунути об’єкти.
3. Якщо потрібно скопіювати виділені об’єкти, після появи значка у вигляді чорної долоні, треба натиснути ліву кнопку миші, потім клавішу Ctrl та, утримуючи їх натисненими, перемістити курсор в потрібне місце.
При роботі в Mathcad постійно користуйтеся правою кнопкою миші. В виникаючому при цьому контекстному меню з’являються, як правило, найбільш необхідні в даний момент пункти, майже завжди присутні пункти Cut (Вирізати), Copy (Копіювати) та Paste (Вставити).
Ø Введіть в робочому документі вирази, які наведені на рис. 1.7. Використайте щодо них всі описані вище процедури редагування.
Ø Виконайте індивідуальні завдання до лабораторної роботи. Підготуйте звіт у вигляді електронного документу.
Індивідуальні завдання до лабораторної роботи №1
1. Обчислити значення арифметичних виразів:
|
1. |
|
11. |
|
|
2. |
|
12. |
|
|
3. |
|
13. |
|
|
4. |
|
14. |
|
|
5. |
|
15. |
|
|
6. |
|
16. |
|
|
7. |
|
17. |
|
|
8. |
|
18. |
|
|
9. |
|
19. |
|
|
10. |
|
20. |
|
2. Обчислити значення виразу:
|
1. |
|
11. |
|
|
2. |
|
12. |
|
|
3. |
|
13. |
|
|
4. |
|
14. |
|
|
5. |
|
15. |
|
|
6. |
|
16. |
|
|
7. |
|
17. |
|
|
8. |
|
18. |
|
|
9. |
|
19. |
|
|
10. |
|
20. |
|
Контрольні запитання:
1. Які функціональні компоненти включає в себе Mathcad?
2. З яких основних елементів складається голвне меню Mathcad?
3. Які особливості введення виразів в Mathcad Вам відомі?
4. Принцип роботи з «чіпкими операторами».
5. Які основні інструменти редагування виразів Вам відомі?
6. Яким чином можна поліпшити роботу в Mathcad?
лабораторна робота № 2
РОЗВ’ЯЗАННЯ ЗАДАЧ ЕЛЕМЕНТАРНОЇ МАТЕМАТИКИ В MATHCAD.
Література до теми: [1-4].
Мета роботи:
1. Познайомитись з можливостями перетворення алгебраїчних виразів в Mathcad.
2. Навчитись працювати з меню Simbolics.
3. Навчитись створювати декартові графіки в Mathcad.
Завдання 2.1. Перетворення алгебраїчних виразів.
Теоретична частина
Основою символьних обчислень в Mathcad є формули та правила їх перетворення, що були запозичені з системи символьної математики Maple 5, що призначена для математиків вищої кваліфікації. Mathcad містить приблизно 20 символьних функцій і цього більш ніж достатньо для розв’язання інженерно-технічних задач.
Ø В головному меню Mathcad виберіть пункт Simbolics, відкриється підменю, що містить ряд команд (рис. 2.1). Для виконання кожної з цих команд необхідно спочатку виділити об’єкт обчислень:
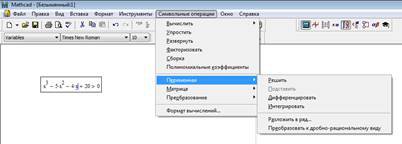
Рис. 2.1. Вид меню Simbolics
Хід роботи:
1. Клацніть мишею на виразі, якщо треба виконати символьну операцію над усім виразом.
2. Якщо треба виконати дії над частиною виразу, виділіть цю частину чорним кольором, тобто підведіть вказівник миші до початку потрібної частини виразу, натисніть ліву кнопку миші та перемістіть курсор до кінця цієї частини при натиснутій лівій кнопці миші.
3. Клацніть мишею на змінній, відносно якої треба виконати символьні дії.
Виділення чорним кольором використовується в Mathcad, коли будь-які дії треба виконати над частиною виразу: вирізати в буфер, скопіювати, видалити, змінити розмір або стиль шрифту тощо.
Виконуючи символьні операції, також треба пам’ятати, що не будь-який вираз піддіється символьним перетворенням, що поставлена задача часто не має символьного рішення (на відміну від чисельного).
4. Змініть Evaluation Style (Стиль обчислень). Для цього оберіть останній пункт меню Simbolics (рис. 2.2). стиль обчислень дозволяє обрати стиль символьного рішення: горизонтально – поруч з вихідним виразом, вертикально – під ним, з коментарями та без них. Виберіть горизонтальний стиль обчислень.
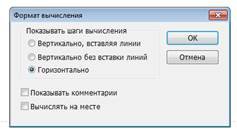
Рис. 2.2. Меню вибору стилю виводу символьного результату
Ø Спростіть наступний вираз: ![]() .
.
Для того щоб спростити даний вираз, використайте меню символьних операцій: натисніть справа внизу біля останнього символу виразу та виділіть його, натискаючи клавішу Space (Пробіл). Потім виберіть в меню Symbolics строчку Simplify (Спростити) (рис. 2..3). Результат (спрощений вираз) буде відображений в робочому документі справа від вихідного виразу.
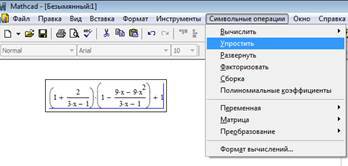
Рис. 2.3. Процес спрощення виразу через меню Symbolics
Ø Розкрийте дужки та приведіть подібні в наступному виразі: x(z+1)2 – 2z(x+z).
Спочатку, як і в попередньому прикладі, встановіть в меню Symbolics режим відображення результатів обчислень – по горизонталі. Потім введіть вираз для перетворення, виділіть його та оберіть пункт меню Symbolics – Expand (Розвернути) (рис. 2.4). Результат (спрощений вираз) буде відображений в робочому документі справа від вихідного виразу.
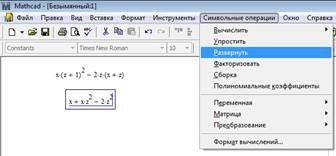
Рис. 2.4. Спрощення виразу з використанням операції Expand
Ø Розкласти на прості дроби раціональний дріб: ![]() .
.
Спочатку, як і в попередньому прикладі, встановіть в меню Symbolics режим відображення результатів обчислень – по горизонталі. Потім виділіть змінну x та оберіть пункт меню Symbolics – Variable (Змінна) - Convert to Partial Fraction (Перетворити у вигляд раціонального дробу) (рис. 2.5).
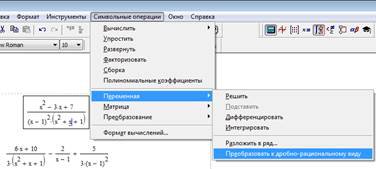
Рис. 2.5. Розкладання на прості дроби з використанням операції Convert to Partial Fraction
Ø Побудувати таблицю значень функції ![]() на відрізку [0, 4p2].
на відрізку [0, 4p2].
Одне з найкращих винаходів Mathcad – це дискретна змінна, що виконує роль оператору циклу. Деякі автори називають її ранжированою змінною. Суть цього поняття полягає в побудові діапазону зміни змінної. Дискретна змінна задає ряд значень змінної, для яких обчислюється функція. Цей ряд значень можна вивести у вигляді графіку або таблиці. Визначення дискретної змінної має вигляд x := 0..5, що означає завдання ряду значень x = 0, 1, 2, 3, 4, 5.
На рис. 2.6 наведений фрагмент робочого документу Mathcad з відповідними обчисленнями:

Рис. 2.6. Побудова таблиці значень функції
Інтервал «..» задається натисканням клавіші «:». Для виведення таблиці, введіть позначення матриці-стовпця F та натисніть знак «=». Клацніть по полю таблиці в робочому документі, щоб відкрити вікно для перегляду всієї таблиці зі стрілками прокрутки.
Ø Побудуйте графік функції ![]() . Для цього введіть в робочому документі Mathcad відповідну функцію. Далі оберіть на панелі інструментів Графік – декартовий графік X-Y і введіть у відкритому шаблоні графіка ім’я функції f(t) по осі ординат, а ім’я аргументу t – по осі абсцис, та клацніть мишею поза рамкою шаблону плаского графіку.
. Для цього введіть в робочому документі Mathcad відповідну функцію. Далі оберіть на панелі інструментів Графік – декартовий графік X-Y і введіть у відкритому шаблоні графіка ім’я функції f(t) по осі ординат, а ім’я аргументу t – по осі абсцис, та клацніть мишею поза рамкою шаблону плаского графіку.
На рис. 2.7 наведений фрагмент робочого документу Mathcad з відповідними обчисленнями та графіком.
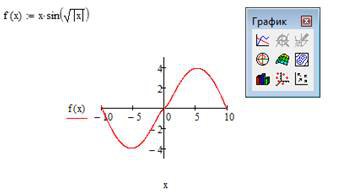
Рис. 2.7. Побудова графіку функції
Ø Розв’язати графічно рівняння: f(x) = 0, де f(x) = x2 + 3x2 – 2.
На рис. 2.8 та 2.9 наведені фрагменти робочого документу Mathcad з відповідними визначниками, графіками та вікнами діалогу.
Спочатку визначте функцію f(x) та побудуйте її графік. Алгоритм дій як і в попередньому завданні. Для того щоб знайти корені рівняння абсциси точок перетину графіку функцій з віссю y = 0, натисніть при виділеному шаблоні побудованого графіку на строчці Trace (Трасування) в пункті Graph (Графік) меню Format (Формат). Потім клацніть по полю графіка та встановіть (стрілками клавіатури або мишею) маркер (пунктирні лінії, що перетинаються) в точці перетину графіка функції з віссю абсцис. У вікні діалогу відображаються координати маркера: значення координати x у вікні є шуканим наближеним значенням кореня рівняння.

Рис. 2.8. Визначення координат точки
|
|
|
|
|
|
Рис. 2.9. Вікна діалогу налаштування декартового графіку
Ø Розв’яжіть символьне рівняння: ![]()
Натисніть на кнопці розв’язання рівнянь ![]() на панелі символьних обчислень
на панелі символьних обчислень ![]() . Введіть в позиції зліва від ключового слова solve ім’я змінної, відносно якої треба розв’язати рівняння, та клацніть по вільному місцю в робочому документі. Результат – значення кореня рівняння буде відображений в робочому документі справа від стрілки (див. рис. 2.10).
. Введіть в позиції зліва від ключового слова solve ім’я змінної, відносно якої треба розв’язати рівняння, та клацніть по вільному місцю в робочому документі. Результат – значення кореня рівняння буде відображений в робочому документі справа від стрілки (див. рис. 2.10).
![]()
Рис. 2.10. Результат символьного розв’язання рівняння
Ø Розв’язати систему нелінійних рівнянь:
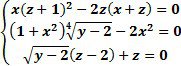
Введіть з клавіатури ключове слово Given (Дано), потім правіше та нижче ключового слова ліву частину першого рівняння системи, далі символьний знак рівності ![]() з панелі Булева алгебра (або введіть з клавіатури Ctrl+=) та праву частину рівняння – 0. Аналогічно введіть решту рівнянь. Правіше та нижче останнього рівняння системи введіть ім’я функції Find (Знайти), перерахуйте в дужках імена змінних, значення яких потрібно знайти, виділіть Find(x,y,z), клацніть по кнопці
з панелі Булева алгебра (або введіть з клавіатури Ctrl+=) та праву частину рівняння – 0. Аналогічно введіть решту рівнянь. Правіше та нижче останнього рівняння системи введіть ім’я функції Find (Знайти), перерахуйте в дужках імена змінних, значення яких потрібно знайти, виділіть Find(x,y,z), клацніть по кнопці ![]() в панелі
в панелі ![]() . Обчислене розв’язання системи буде відображене після натискання мишею поза рамкою виділення в робочому документі справа від стрілки у вигляді матриці, кожний стовбець якої містить одне з рішень системи. В наведеному прикладі, знайдені два рішення системи: x=0, y=2, z=0 та x=1, y=3, z=1.
. Обчислене розв’язання системи буде відображене після натискання мишею поза рамкою виділення в робочому документі справа від стрілки у вигляді матриці, кожний стовбець якої містить одне з рішень системи. В наведеному прикладі, знайдені два рішення системи: x=0, y=2, z=0 та x=1, y=3, z=1.
Нижче наведений фрагмент робочого документу Mathcad з відповідними обчисленнями (рис. 2.11).
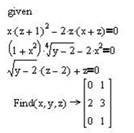
Рис. 2.11. Результат розв’язання системи нелінійних рівнянь
Ø Виконайте індивідуальні завдання до лабораторної роботи. Підготуйте звіт у вигляді електронного документу.
Індивідуальні завдання до лабораторної роботи №2
1. Спростити вираз:
|
1. |
|
11. |
|
|
2. |
|
12. |
|
|
3. |
|
13. |
|
|
4. |
|
14. |
|
|
5. |
|
15. |
|
|
6. |
|
16. |
|
|
7. |
|
17. |
|
|
8. |
|
18. |
|
|
9. |
|
19. |
|
|
10. |
|
20. |
|
2. Розкрити дужки та привести подібні у виразі:
|
1. |
|
11. |
|
|
2. |
|
12. |
|
|
3. |
|
13. |
|
|
4. |
|
14. |
|
|
5. |
|
15. |
|
|
6. |
|
16. |
|
|
7. |
|
17. |
|
|
8. |
|
18. |
|
|
9. |
|
19. |
|
|
10. |
|
20. |
|
3. Розкласти на множники вираз:
|
1. |
|
11. |
|
|
2. |
|
12. |
|
|
3. |
|
13. |
|
|
4. |
|
14. |
|
|
5. |
|
15. |
|
|
6. |
|
16. |
|
|
7. |
|
17. |
|
|
8. |
|
18. |
|
|
9. |
|
19. |
|
|
10. |
|
20. |
|
4. Розкласти на прості дроби раціональний дріб:
|
1. |
|
11. |
|
|
2. |
|
12. |
|
|
3. |
|
13. |
|
|
4. |
|
14. |
|
|
5. |
|
15. |
|
|
6. |
|
16. |
|
|
7. |
|
17. |
|
|
8. |
|
18. |
|
|
9. |
|
19. |
|
|
10. |
|
20. |
|
5. Розв’язати символьне рівняння:
|
1. |
|
11. |
|
|
2. |
|
12. |
|
|
3. |
|
13. |
|
|
4. |
|
14. |
|
|
5. |
|
15. |
|
|
6. |
|
16. |
|
|
7. |
|
17. |
|
|
8. |
|
18. |
|
|
9. |
|
19. |
|
|
10. |
|
20. |
|
6. Розв’язати символьне рівняння:
|
1. |
|
11. |
|
|
2. |
|
12. |
|
|
3. |
|
13. |
|
|
4. |
|
14. |
|
|
5. |
|
15. |
|
|
6. |
|
16. |
|
|
7. |
|
17. |
|
|
8. |
|
18. |
|
|
9. |
|
19. |
|
|
10. |
|
20. |
|
Контрольні запитання:
1.Які перетворення алгебраїчних виразів в Mathcad Вам відомі?
2.Які формати обчислень в Mathcad Вам відомі?
3.В чому полягає зміст зміни формату обчислень?
4.В чому полягає суть поняття «дискретна змінна»?
5. В чому полягає принцип побудови декатових графіків в Mathcad?
6. Для чого використовується інструмент Трасування?
7. Які функції використовуються для символьного розв’язання рівнянь?
лабораторна робота № 3
РОЗВ’ЯЗАННЯ СИСТЕМ ЛІНІЙНИХ АЛГЕБРАЇЧНИХ РІВНЯНЬ ЗА ФОРМУЛАМИ КРАМЕРА. МАТРИЧНА ФОРМА ЗАПИСУ ЛІНІЙНИХ СИСТЕМ.
Література до теми: [1-4].
Мета роботи.
1. Ознайомитись зі способами створення масивів чисел в Mathcad.
2. Ознайомитись зі способами розв’язання систем лінійних алгебраїчних рівнянь.
3. Ознайомитися зі способом розв’язання матричних рівнянь.
Завдання 3.1. Розв’язання систем лінійних алгебраїчних рівнянь за формулами Крамера.
Теоретична частина
В Mathcad є три способи створення масиву чисел:
1. Заповнення шаблону матриць, що містить порожні місця введення чисел, що підходить для введення невеликих масивів (не більше 100 елементів).
2. Використання дискретної змінної. Цей метод підходить, коли є явна формула для обчислення елементів масиву.
3. Зчитування даних з файлів. Наприклад, з електронної книги Excel. В Mathcad існує три функції, що дозволяють зчитувати дані з інших файлів або записати числові дані в інший файл:
APPENPRN («file») – додає числові дані в існуючий файл. Тут file – ім’я файлу або шлях до файлу, якщо він знаходиться в іншому каталозі;
READPRN («file») – зчитує числові дані з файлу;
WRITEPRN («file») – записує числові дані в файл.
Всі три функції працюють тільки з файлами, в яких числа створюють прямокутну матрицю (вектор чисел – окремий випадок прямокутної матриці).
Ø Дослідіть та, якщо рішення існує, знайдіть за формулами Крамера рішення системи:
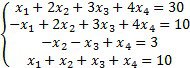
Хід роботи:
1. Встановіть режим автоматичних обчислень та режим відображення результатів обчислень – по горизонталі.
2. Надайте змінній ORIGIN значення, що дорівнює 1.
Початок нумерації елементів в векторах та матрицях визначаються вбудованою змінною ORIGIN. За умовчанням ORIGIN = 0, тобто перший елемент вектору, перша строчка та перший стовбець матриці мають індекс нуль.
Щоб змінити нумерацію індексів в першій строчці документа необхідно набрати з клавіатури - ORIGIN:=1. Можна перевизначити вбудовану змінну ORIGIN іншим способом. Виберіть в головному меню команду Tools (Інструменти) ® Worksheet Options (Параметри документу), та у вікні, що відкриється перейдіть на вкладку Built-ln Variables (Вбудовані змінні) і в полі Array Origin (ORIGIN) введіть індекс першого елементу масиву (рис. 3.1). Змінній ORIGIN можна надавати різних значень, в тому числі і від’ємних.
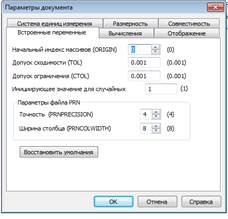
Рис. 3.1. Вбудовані змінні Mathcad
3. Введіть матрицю лівої частини та стовбець правої частин рівняння.
Для цього встановіть курсор в те місце, де треба створити матрицю. Натисніть на кнопці математичної панелі Vector and Matrix Toolbar (Вектори та матриці), а у панелі інструментів, що з’явиться на екрані натисніть на кнопку Matrix or Vector (Матриця або вектор) (див. рис. 3.2.). В діалоговому окні введіть число строчок (Rows) та число стовпців (Columns) та натисніть кнопку OK.
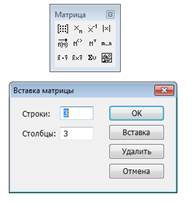
Рис. 3.2. Панелі для роботи з матрицями
Перехід від одного місця введення до іншого здійснюється клавішами зі стрілками або натисканням мишею в потрібному місці.
Ø Обчисліть визначник матриці та визначники матриць, отриманих заміною відповідного стовпця, стовпцем правих частин. Знайдіть за формулами Крамера рішення системи.
Нижче наведений фрагмент робочого документу Mathcad з відповідними обчисленнями (рис. 3.3).

Рис. 3.3. Результат розв’язання в Mathcad
системи лінійних алгебраїчних рівнянь за формулами Крамера
Завдання 3.2. Розв’язання матричних рівнянь в Mathcad.
Теоретична частина
Матриця А, стовпцями якої є коефіцієнти при відповідних невідомих, а строчками коефіцієнти при невідомих у відповідному рівнянні називається матрицею системи. Матриця-стовбець b, елементами якої є праві частини рівнянь системи, називається матрицею правої частини або просто правою частиною системи. Матриця-стовпець x, елементи якої шукані невідомі, називається рішенням системи.
Таким чином, система лінійних алгебраїчних рівнянь може бути записана в матричному вигляді у вигляді простого матричного рівняння: Ax = b.
Якщо матриця система невирождена, то в неї існує зворотна матриця, в такому випадку рішення системи можна отримати, помноживши обидві частини рівняння Ax = b зліва на матрицю A-1:
A-1´( Ax) = A-1´( b),
а оскільки A-1A = E та Ex = x, то x = A-1b.
Ø Розв’яжіть систему лінійних алгебраїчних рівнянь в матричному вигляді:
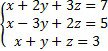
Хід роботи:
1. Встановіть режим автоматичних обчислень та режим відображення результатів обчислень – по горизонталі.
2. Введіть матрицю системи та матрицю-стовпець правих частин.
3. Обчисліть рішення системи за формулою x = A-1b та перевірте правильність рішення помноживши матрицю системи на вектор стовпець рішення.
4. Знайдіть рішення системи за допомогою функції lsolve та порівняйте результати обчислень.
Для розв’язання систем лінійних рівнянь в Mathcad існує вбудована функція lsolve(A,b), яка повертає вектор X для системи лінійних рівнянь при заданій матриці коефіцієнтів A та векторі вільних членів b.
Нижче наведений фрагмент робочого документу Mathcad з відповідними обчисленнями (рис. 3.3).
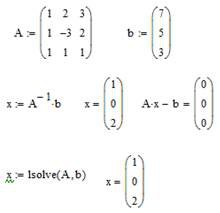
Рис. 3.3. Результат розв’язання в Mathcad
матричних рівнянь
Ø Виконайте індивідуальні завдання до лабораторної роботи. Підготуйте звіт у вигляді електронного документу.
Індивідуальні завдання до лабораторної роботи №3
1. Дослідіть та, якщо рішення існує, знайдіть за формулами Крамера рішення системи Ах = b:
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
|
5. |
|
|
6. |
|
|
7. |
|
|
8. |
|
|
9. |
|
|
10. |
|
|
11. |
|
|
12. |
|
|
13. |
|
|
14. |
|
|
15. |
|
|
16. |
|
|
17. |
|
|
18. |
|
2. Розв’яжіть матричне рівняння Ах = b. Систему лінійних алгебраїчних рівнянь візьміть з попередніх індивідуальних рівнянь.
Контрольні запитання:
1. Які способи створення масиву чисел в Mathcad Вам відомі?
2. Які функції використовуються для зчитування масивів даних з інших файлів?
3. Зміст функції ORIGIN?
4. Функція lsolve та її параметри.
лабораторна робота № 4
ДОСЛІДЖЕННЯ ФУНКЦІЙ НА ЕКСТРЕМУМ ТА ПОШУК КОРЕНІВ РІВНЯНЬ.
Література до теми: [1-4].
Мета роботи:
1. Навчитись досліджувати функції в Mathcad.
2. Ознайомитися зі способами дослідження функцій на екстремум в Mathcad.
Завдання 4.1. Навчитися досліджувати функції на екстремум засобами Mathcad.
Теоретична частина
Пошук екстремуму функції включає в себе задачі знаходження локального та глобального екстремуму. Mathcad за допомогою вбудованих функцій вирішує задачу знаходження тільки локального екстремуму. Для пошуку глобального екстремуму необхідно обчислити всі локальні екстремуми та вибрати з них найбільший або найменший. В Mathcad існує три шляхи пошуку екстремуму:
1. Для безперервної функції використовується прирівнювання нулю похідної від функції.
2. Для функції з переломами використовують функцію minerr. Для цього по графіку обирається число, що є більшим (або меншим) за екстремальне значення функції, та записують його в якості обмеження в блоці Given. Функція minerr повертає значення аргументу, при якому розбіжність між заданим числом та значенням функції мінімальне, на тій ділянці, де вибране початкове наближення.
3. для безперервних функцій зручно використовувати функції maximize та minimize (вони вводяться аналогічно функції find). Ключове слово Given можна опустити – воно необхідне лише при наявності обмежень.
Ø Знайти найбільше та найменше значення функції f(x) = 2x∙ 4x на відрізку [0, 1]. Розв’яжіть на цьому відрізку рівняння 2x ∙ 4x = 0.
Хід роботи:
1. Встановіть автоматичний режим обчислень та режим відображення результатів символьних обчислень - по горизонталі.
2. Визначте вираз для функції.
3. Побудуйте графік функції.
4. Знайдіть найбільше та найменше значення функції на відрізку.
5. Розв’яжіть рівняння f(x) = 0, використовуючи функцію root та вибравши в якості нульового наближення спочатку ліву, а потім праву межу заданого відрізку.
Нижче наведений фрагмент робочого документу Mathcad з відповідними обчисленнями (рис. 4.1).

Рис. 4.1. Результат розв’язання рівняння в Mathcad
Функція, що розглянута в прикладі, безперервна на відрізку та монотонно спадає на ньому. Найбільшого значення функція набуває в лівому кінці відрізку, в точці x = 0, найменшого в правому кінці, в точці x = 1. Для обчислення нуля функції на відрізку, була використана вбудована функція root(f, x). Перед звертанням до root(f, x) необхідно надати змінній x початкового значення. В наведеному фрагменті корінь обчислювався двічі, в якості початкового наближення були використані спочатку лівий, а потім правий кінець відрізку.
Ø Знайдіть графічно корінь рівняння.
Для того щоб знайти корінь рівняння графічно, використайте операцію обчислення координат точки на кривій. Більш точні значення координат кореня можна отримати, збільшивши графік в околиці кореня, за допомогою операції Zoom (Масштаб) пункту Graph (Графік) меню Format (Формат).
Нижче наведений фрагмент робочого документу Mathcad в якому наведені результати відповідних операцій та графік функції на проміжку [0;6] рис. 4.2.

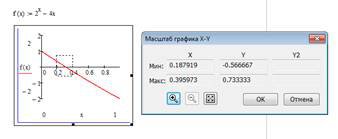
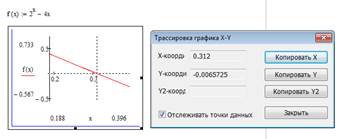
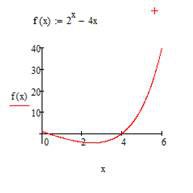
Рис. 4.2. Графічне знаходження коренів рівняння в Mathcad
Ø Виконайте індивідуальні завдання до лабораторної роботи. Підготуйте звіт у вигляді електронного документу.
Індивідуальні завдання до лабораторної роботи №4
1. Знайдіть (аналітично та графічно) точки, в яких досягаються найбільше та найменше значення заданої на відрізку безперервної функції. Знайдіть нуль функції на заданому відрізку. Розв’яжіть рівняння f(x) = 0:
|
№ |
Функція |
Відрізок |
|
1. |
|
[0; 6] |
|
2. |
|
[1; 4] |
|
3. |
|
[1; 4] |
|
4. |
|
[-3; 3] |
|
5. |
|
[0; 4] |
|
6. |
|
[-1; 5] |
|
7. |
|
[1; 9] |
|
8. |
|
[0; 3] |
|
9. |
|
[-3; 3] |
|
10. |
|
[2; 4] |
|
11. |
|
[-1; 2] |
|
12. |
|
[-1; 6] |
|
13. |
|
[1; 4] |
|
14. |
|
[-1; 7] |
|
15. |
|
[1; 5] |
|
16. |
|
[-4; 2] |
|
17. |
|
[-4; -1] |
|
18. |
|
[-2; 4] |
Контрольні запитання:
1. Які шляхи пошуку екстремумів функцій в Mathcad Вам відомі.
2. Функція minerr та особливості її застосування.
3. Функції maximize та minimize та особливості їх застосування.
4. Функція root та особливості її застосування?
5. В чому полягає принцип графічного пошуку коренів рівняння?
лабораторна робота № 5
РОЗГАЛУЖЕНІ ОБЧИСЛЮВАЛЬНІ ПРОЦЕСИ В СЕРЕДОВИЩІ MATHCAD.
Література до теми: [1-4].
Мета роботи:
1. Познайомитись з особливостями застосування функції if.
2. Познайомитись з особливостями застосування умовного оператора if.
3. Познайомитись з особливостями застосування пакету Mathcad в задачах математичної статистики.
Завдання 5.1. Використання умовної функції if в Mathcad.
Теоретична частина
Mathcad виконує оператори програм в порядку згори до низу (лінійний обчислювальний процес). Але за необхідності в Mathcad може бути організоване розгалуження. Цього можна досягти за допомогою кусочно-безперервної функції if або використовуючи умовний оператор if.
Функція if використовується для визначення функціональних залежностей, які поводять себе по різному зліва та зправа від деякої точки:
if(cond, tval, fval)
де cond (умова) – перший аргумент функції if. Якщо значення cond істина (або 1), то результатом буде значення другого аргументу tval (true value), інакше, якщо cond ложь (або 0) буде обчислене значення третього аргументу fval (false value).
Хід роботи:
Ø Обчислити значення кусочно-безперервних функцій g(x) та h(x). Побудуйте графіки функцій g(x) та h(x). Аргумент x змінюється на проміжку [-2, 2] з кроком 0,2. Побудуйте графіки функцій g(x) та h(x).
![]()
![]()
Нижче наведений фрагмент робочого документу Mathcad в якому наведені результати відповідних обчислень (див. рис. 5.1).
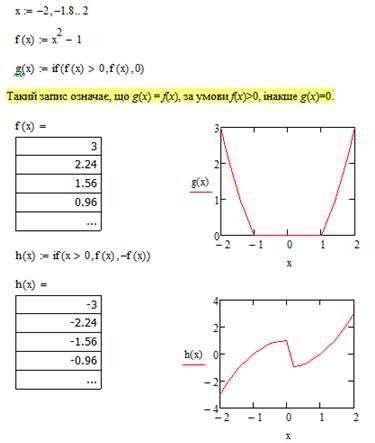
Рис. 5.1. Результат обчислень значень кусочно-безперервної функції
за допомогою функції if
Завдання 5.2. Використання умовного оператора if в Mathcad.
Теоретична частина
Дія умовного оператора if складається з двох частин. Спочатку перевіряється умова, що записана справа від оператора if. Якщо умова є вірною, виконується вираз, що знаходиться зліва від умовного оператора if. Якщо умова не вірна, відбувається перехід до наступної строчки програми.
Щоб вставити умовний оператор if в Mathcad, необхідно:
1. Встановити курсор у вільному місці робочого документу Mathcad.
2. На панелі Programming Toolbar (Програмування) клацнути на кнопці if. В робочому документі з’явиться шаблон оператора з двома місцями введення.
3. Спарава від оператора if вводиться умова, при цьому можна користуватися логічними операторами, вводячи їх з панелі Boolean (Булеві оператори), а зліва від оператора if вводиться вираз, який повинен виконуватися, якщо умова є вірною.
4. Якщо при виконанні умови повинні виконуватися одразу кілька виразів, треба мати кілька місь введення. Для цього необхідно встановити курсор на місце введення зліва від умовного оператора of та натиснути Add Line (Додати строчку програми) з панелі Програмування стільки разів, скільки строчок треба ввести.
Хід роботи:
Ø Обчислити значення кусочно-безперервної функції f(x) з використанням умовного оператора if. Аргумент x змінюється на проміжку [-2, 2] з кроком 0,2. Побудуйте графік функції f(x).
![]()
Нижче наведений фрагмент робочого документу Mathcad в якому наведені результати відповідних обчислень (див. рис. 5.2).
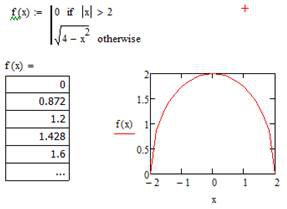
Рис. 5.2. Результат обчислень значень кусочно-безперервної функції
за допомогою умовного оператора if
Завдання 5.3. Використання умовного оператора if для побудови функції розподілу випадкової величини в Mathcad.
Теоретична частина
Mathcad має розвинений апарат роботи з задачами математичної статистики. З одного боку, Mathcad містить велику кількість вбудованих спеціальних функцій, що дозволяють обчислювати щільності, ймовірності та інші основні характеристики основних законів розподілу випадкових величин.
З іншого боку, в Mathcad запрограмована відповідна кількість генераторів псевдовипадкових чисел для кожного закону розподілу, що дозволяє ефективно проводити моделювання методами Монте-Карло. Є можливість будувати гістограми та розраховувати статистичні характеристики вибірок випадкових чисел та випадкових процесів, таких як середні, дисперсії, кореляції тощо. При цьому випадкові послідовності можуть як створюватись генераторами випадкових чисел, так і вводитися користувачем з файлів.
Нагадаємо, що дискретна випадкова величина x, що приймає значення x1 < x2 < … < xi < … з ймовірностями p1, p2, …, pi, … може бути задана розподілом – таблицею наступного вигляду:
|
x |
x1 |
x2 |
… |
xi |
… |
xn |
|
p |
p1 |
p2 |
… |
pi |
… |
pn |
Такі таблиці в середовищі Mathcad зручно зберігати у вигляді матриці з розмірністю 2´n. Функція розподілу випадкової величини, що має наведений вище розподіл, має вигляд:
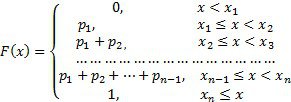
Ø Побудувати графік функції накопичення випадкової величини, що має наступний розподіл:
|
x |
1 |
0 |
7 |
4 |
-2 |
|
p |
0,1 |
0,5 |
0,1 |
0,1 |
0,2 |
Нижче наведений фрагмент робочого документу Mathcad в якому наведені результати відповідних обчислень (див. рис. 5.3).
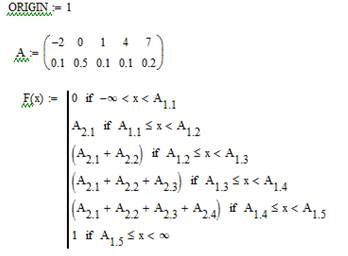
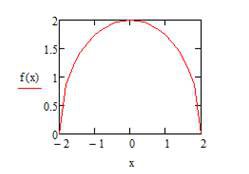
Рис. 5.3. Результат побудови функції розподілу випадкової величини в Mathcad
Завдання 5.4. Застосування умовного оператора if в задачах розкладення кусочно-безперервних функцій в ряд Фур’є в Mathcad.
Теоретична частина
Для безперервної періодичної функції f(x) на відрізку [-p, p] можна поставити у відповідність ряд часткових сум Фур’є S(x):
f(x) ~ S(x).
Обчислення часткових сум ряду Фур’є виконується за наступною формулою:
![]()
де ak та bk – коефіцієнти Фур’є, які обчислюються за формулами Ейлера-Фур’є:
![]()
![]()
Ø Побудувати графік f(x). Побудувати графіки часткових сум для n = 5, 10, 25, 50, 100: S(x, 5), S(x, 10), S(x, 25), S(x, 50), S(x, 100), та порівняти їх між собою та з графіком f(x).
Функція f(x) має наступний вигляд:
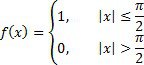
Нижче наведений фрагмент робочого документу Mathcad в якому наведені результати відповідних обчислень (див. рис. 5.4).
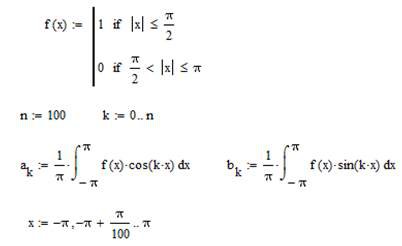
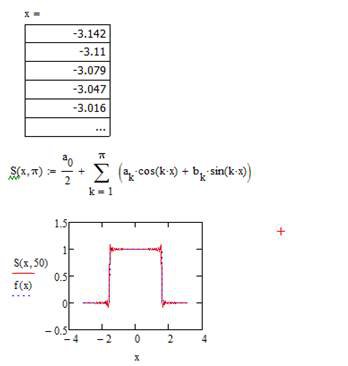
Рис. 5.4. Результат побудови ряду Фур'є в Mathcad
Ø Виконайте індивідуальні завдання до лабораторної роботи. Підготуйте звіт у вигляді електронного документу.
Індивідуальні завдання до лабораторної роботи №5
1. Побудувати графік функції накопичення випадкової величини, що має наступний розподіл:
|
1. |
|
||||||||||||||||
|
2. |
|
||||||||||||||||
|
3. |
|
||||||||||||||||
|
4. |
|
||||||||||||||||
|
5. |
|
||||||||||||||||
|
6. |
|
||||||||||||||||
|
7. |
|
||||||||||||||||
|
8. |
|
||||||||||||||||
|
9. |
|
||||||||||||||||
|
10. |
|
||||||||||||||||
|
11. |
|
||||||||||||||||
|
12. |
|
||||||||||||||||
|
13. |
|
||||||||||||||||
|
14. |
|
||||||||||||||||
|
15. |
|
||||||||||||||||
|
16. |
|
||||||||||||||||
|
17. |
|
||||||||||||||||
|
18. |
|
||||||||||||||||
|
19. |
|
||||||||||||||||
|
20. |
|
Контрольні запитання:
1. Використання умовної функції if в Mathcad.
2. Використання умовного оператора if в Mathcad.
3. Принцип розв’язання задач математичної статистики за допомогою Mathcad?
4. Застосування умовного оператора if в задачах дослідження кус очно-безперервних функцій?
5. Панель Програмування та принципи її використання?
лабораторна робота № 6
ПОХІДНА ТА ЇЇ ОБЧИСЛЕННЯ
Література до теми: [1-4, 6].
Мета роботи:
1. Познайомитись з особливостями знаходження похідної в Mathcad.
2. Познайомитися зі способами визначення похідних в Mathcad
Завдання 6.1. Знаходження похідної функції в Mathcad.
Теоретична частина
За допомогою меню Symbolics (Символьні операції) похідну можна обчислити двома способами:
1. В потрібному виразі, записаному без знаків похідної виділити змінну, за якою треба обчислити похідну. В головному меню оберіть команду Symbolics (Символьні операції) ® Variable (Змінна) ® Differentiate (Диференціювати).
2. На панелі Calculus (Обчислення) оберіть знак похідної та запишіть з його допомогою потрібний вираз. В головному меню виберіть команду Symbolics (Символьні операції) ® Evaluate (Обчислити) ® Symbolically (Символьно).
Ø Знайдіть похідну функції:
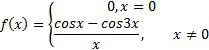
Обчисліть значення похідної в точці x = 0. Оскільки f(0) = 0, то приріст функції Df(x) в точці х = 0 дорівнює Df(0) = f(0 + Dx) - f(0) = f(Dx) - f(0) = f(Dx).
Хід роботи:
1. Встановіть режим відображення результатів – по горизонталі.
2. Визначте функцію.
3. Визначте приріст функції у вказаній точці.
4. Обчисліть межу відношення приросту функції до приросту аргументу при прагненні приросту аргументу до нуля.
5. Обчисліть похідну аналітично.
Нижче наведений фрагмент робочого документу Mathcad в якому наведені результати відповідних обчислень (див. рис. 6.1).
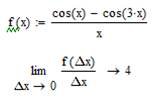
Рис. 6.1. Обчислення похідної функції в Mathcad
Ø Знайдіть похідну функції з попереднього завдання використовуючи другий спосіб.
Нижче наведений фрагмент робочого документу Mathcad в якому наведені результати відповідних обчислень (див. рис. 6.2).
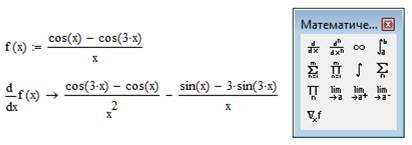
Рис. 6.6. Диференціювання за допомогою панелі інструментів
Calculus (Обчислення)
Ø Виконайте індивідуальні завдання до лабораторної роботи. Підготуйте звіт у вигляді електронного документу.
Індивідуальні завдання до лабораторної роботи №6
1. Знайдіть похідну функції f(x). Обчисліть значення похідної в точці x = 0, маючи на увазі, що f(0) = 0:
|
f(x) |
f(x) |
||
|
1. |
|
11. |
|
|
2. |
|
12. |
|
|
3. |
|
13. |
|
|
4. |
|
14. |
|
|
5. |
|
15. |
|
|
6. |
|
16. |
|
|
7. |
|
17. |
|
|
8. |
|
18. |
|
|
9. |
|
19. |
|
|
10. |
|
20. |
|
Контрольні запитання:
1. Якими способами можна обчислити похідну в Mathcad?
2. В чому полягає алгоритм обчислення похідної в Mathcad?
3. Яким чином можна перевірити правильність отриманих результатів?
лабораторна робота № 7
НЕВИЗНАЧЕНИЙ ІНТЕГРАЛ. ІНТЕГРУВАННЯ ЗАМІНОЮ ЗМІННОЇ
Література до теми: [1-4].
Мета роботи:
1. Навчитися обчислювати невизначений інтеграл.
2. Познайомитися зі способами обчислення невизначених інтегралів в Mathcad.
Завдання 7.1. Визначити невизначений інтеграл. Навчитися перевіряти правильність отриманих результатів.
Теоретична частина
За допомогою меню Symbolics (Символьні операції) інтеграл можна обчислити двома способами:
1. В потрібному виразі, записаному без знаків інтегралу виділити змінну, за якою треба обчислити інтеграл. В головному меню оберіть команду Symbolics (Символьні операції) ® Variable (Змінна) ® Integrate (Інтегрувати).
2. На панелі Calculus (Обчислення) оберіть знак інтегралу та запишіть з його допомогою потрібний вираз. В головному меню виберіть команду Symbolics (Символьні операції) ® Evaluate (Обчислити) ® Symbolically (Символьно).
Ø Обчисліть невизначений інтеграл:
![]() ,
,
та перевірте правильність отриманих результатів. Побудуйте графіки сімейства перешообразних.
Хід роботи:
1. Встановіть автоматичний режим обчислень та режим відображення результатів обчислень – по горизонталі.
2. Визначте підінтегральну функцію як функцію змінної x.
3. Знайдіть першообразну, використовуючи символьну математику Mathcad.
4. Визначте першообразну як функцію змінної.
5. Знайдіть похідну першообразної, використовуючи символьну математику Mathcad.
6. Спростіть похідну від першообразної, порівняйте результат з підінтегральною функцією.
7. Побудуйте на одному графіку зображення декілька першообразних.
Нижче наведений фрагмент робочого документу Mathcad в якому наведені результати відповідних обчислень (див. рис. 7.1).
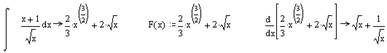
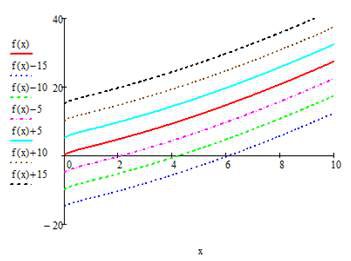
Рис. 7.1. Визначення невизначеного інтегралу в Mathcad
Ø Обчислити невизначений інтеграл:
![]() ,
,
заміною змінних.
Хід роботи:
1. Для того щоб виконати в невизначеному інтегралі заміну змінної x новою змінною:
![]() ,
,
необхідно ввести в робочому документі вираз:
![]() ,
,
та розв’язати його відносно змінної x (виділивни x, і клацнувши по строчці Solve (Розв’язати) в пункті Variable (Змінна)), потім продиференціювати отриманий вираз по t.
2. Скопіюйте в робочий документ підінтегральну функцію змінної x, скопіюйте в буфер обміну вираз для x та виконайте заміну (виділіть x, та клацніть по строчці Substitute (Замінити) в пункті Variable (Змінна) меню Symbolics (Символьні операції).
3. Обчисліть невизначений інтеграл.
4. Виконайте зворотну підстановку (замініть змінну t її виразом через x).
5. Спростіть вираз (розкладіть на множники), використовуючи меню Symbolics (Символьні операції), пункт Factor (Факторизувати).
6. Проведіть перевірку отриманих результатів. Продиференціюйте отриманий вираз по x та спростіть.
Нижче наведений фрагмент робочого документу Mathcad в якому наведені результати відповідних обчислень (див. рис. 7.2).
![]()
![]()
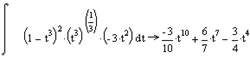
![]()
![]()
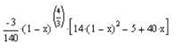
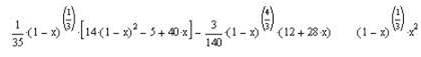
Рис. 7.1. Визначення невизначеного інтегралу заміною змінної
в Mathcad
Ø Виконайте індивідуальні завдання до лабораторної роботи. Підготуйте звіт у вигляді електронного документу.
Індивідуальні завдання до лабораторної роботи №7
1. Обчисліть невизначений інтеграл ![]() та перевірте правильність обчислень. Побудуйте графіки сімейства першообразних:
та перевірте правильність обчислень. Побудуйте графіки сімейства першообразних:
|
f(x) |
f(x) |
||
|
1. |
|
11. |
|
|
2. |
|
12. |
|
|
3. |
|
13. |
|
|
4. |
|
14. |
|
|
5. |
|
15. |
|
|
6. |
|
16. |
|
|
7. |
|
17. |
|
|
8. |
|
18. |
|
Контрольні запитання:
1. Якими способами можна обчислити інтеграл в Mathcad?
2. В чому полягає алгоритм обчислення невизначеного інтегралу в Mathcad?
3. Яким чином можна перевірити правильність отриманих результатів?
4. Яким чином відбувається обчислення інтегралу заміною змінної в Mathcad?
лабораторна робота № 8
ВИЗНАЧЕНИЙ ІНТЕГРАЛ
Література до теми: [1-4].
Мета роботи:
1. Навчитися обчислювати визначений інтеграл.
2. Навчитись досліджувати поведінку інтегральних сум на заданому відрізку інтегрування в Mathcad.
Завдання 8.1. Визначення та обчислення визначеного інтегралу.
Теоретична частина
За допомогою меню Symbolics (Символьні операції) визначений інтеграл можна обчислити двома способами:
1. В потрібному виразі, записаному без знаків інтегралу виділити змінну, за якою треба обчислити інтеграл. В головному меню оберіть команду Symbolics (Символьні операції) ® Variable (Змінна) ® Integrate (Інтегрувати).
2. На панелі Calculus (Обчислення) оберіть знак інтегралу та запишіть з його допомогою потрібний вираз. В головному меню виберіть команду Symbolics (Символьні операції) ® Evaluate (Обчислити) ® Symbolically (Символьно).
Ø Обчисліть значення інтегралу від лінійної функції. Визначити площу відповідної фігури. Записати вираз для інтегральних сум (при розбиванні відрізку інтегрування на N рівних частин довжиною:
![]() ,
,
знайти межі інтегральних сум від N до D.
f(x):= ![]() , a:= 1, b:= 5.
, a:= 1, b:= 5.
Нижче наведений фрагмент робочого документу Mathcad в якому наведені результати відповідних обчислень (див. рис. 8.1).
Хід роботи:
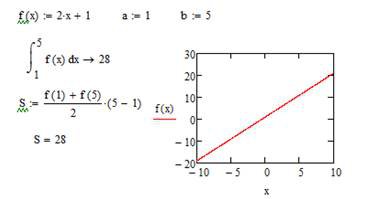
Рис. 8.1. Обчислення визначеного інтегралу в Mathcad
1. Для заданої функції дослідіть поведінку інтегральних сум на заданому відрізку інтегрування, розбиваючи відрізок інтегрування на рівні частини. Обчисліть визначений інтеграл та порівняйте його значення зі значеннями меж інтегральних сум.
2. Встановіть автоматичний режим обчислень та режим відображення результатів – по горизонталі.
3. Визначте підінтегральну функцію, як функцію змінної x та побудуйте її графік.
4. Обчисліть визначений інтеграл.
5. Запишіть вираз для інтегральної суми, отриманій при розбиванні відрізка інтегрування на рівні частини, коли значення функції обчислюється в лівому кінці відрізку розбивання. Знайдіть її межу при числі відрізків розбивання, що прагнуть до нескінченності.
6. Запишіть вираз для інтегральної суми, отриманої при розбиванні відрізку інтегрування на рівні частини, коли значення функції обчислюється в правому кінці відрізку розбивання. Знайдіть її межу при числі відрізків розбивання, що прагне до нескінченності.
Ø Запишіть вираз для інтегральної суми, що отримана при розбиванні відрізку інтегрування на рівні частини, коли значення функції обчислюється в середині відрізку розбивання. Знайдіть її межу при числі відрізків розбивання, що прагнуть до нескінченності.
Хід роботи:
1. Порівняйте отримані значення меж між собою та зі значенням інтегралу.
2. Побудуйте графіки інтегральних сум як функцій числа розбивання відрізків інтегрування.
3. Побудуйте графіки інтегральних сум як функцій довжини відрізків розбивання.
Нижче наведений фрагмент робочого документу Mathcad в якому наведені результати відповідних обчислень (див. рис. 8.2).
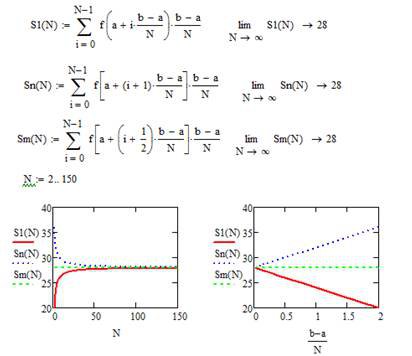
Рис. 8.1. Дослідження поведінки інтегральних сум на заданому відрізку інтегрування в Mathcad
Ø Виконайте індивідуальні завдання до лабораторної роботи. Підготуйте звіт у вигляді електронного документу.
Індивідуальні завдання до лабораторної роботи №8
1. Обчисліть визначений інтеграл ![]() безпосередньо за допомогою заміни змінних:
безпосередньо за допомогою заміни змінних:
|
f(x) |
[a; b] |
f(x) |
[a; b] |
||
|
1. |
|
[0; 16] |
11. |
|
[0,4; |
|
2. |
|
[0; 1] |
12. |
|
[0,2; |
|
3. |
|
[0; 5] |
13. |
|
[0; |
|
4. |
|
[3; 5] |
14. |
|
[6; 9] |
|
5. |
|
[0; |
15. |
|
[8; 12] |
|
6. |
|
[0; |
16. |
|
[6; 10] |
|
7. |
|
[0; 4] |
17. |
|
[0; 3] |
|
8. |
|
[0; 2] |
18. |
|
[1; 64] |
|
9. |
|
[0; 4] |
19. |
|
[0; 3] |
|
10. |
|
[0; 9] |
20. |
|
[0; 1] |
Контрольні запитання:
1. В чому полягає суть обчислення визначеного ітегралу?
2. Яким чином досліджують поведінку інтервальних сум на заданому відрізку інтегрування в Mathcad?
3. Які способи обчислення визначених інтегралів Вам відомі?
ЗАПИТАННЯ ДЛЯ МОДУЛЬНОГО КОНТРОЛЮ З МОДУЛЯ 1 “МІСЦЕ САПР В ПРОЕКТУВАННІ БУДІВЕЛЬ ТА СПОРУД”
(теоретичний матеріал)
1. Дайте визначення САПР.
2. На які укрупнені етапи можна розділити процес проектування на базі САПР?
3. Які функції виконує автоматизована система управління підприємством (АСУП)?
4. Схематично зобразіть етапи життєвого циклу промислових виробів.
5. Дайте визначення абревіатурі CAD, CAE, CAM.
6. Які функції виконує система управління ланцюжками постачань (SCM)?
7. Дайте визначення абревіатурі PDM, SCM, CPC.
8. Наведіть характерні особливості систем з ієрархічною структурою.
9. Дайте визначення абревіатурі АСУП, ERP, MRP-2, MES.
10. Дайте визначення абревіатурі SCADA, СNC, IETM, PLM.
11. Які види забезпечення є в САПР?
12. Які функції в структурі САПР виконують підсистеми що проектують і обслуговуючі?
13. Якими на Вашу думку, є основні принципи створення САПР?
14. Які основні принципи створення САПР Вам відомі?
15. Які види САПР Вам відомі?
16. Які функції повинні виконувати інтегровані САПР?
17. Назвіть основні особливості технології автоматизованого проектування.
18. Який комплекс вимог пред'являє до САПР реалізація технології автоматизованого проектування?
19. Назвіть найбільш характерні відмітні особливості ГСАПР.
20. Дайте характеристику поняттям висхідне і низхідне проектування.
21. Назвіть основні завдання конструкторського проектування.
22. Що являє собою інформаційне забезпечення САПР?
23. Яким є основне завдання архітектурного рівня проектування?
24. Що є головною метою створення інформаційного забезпечення САПР?
25. Які основні вимоги до інформаційного забезпечення САПР?
26. Що відбувається на етапі робочого проектування?
27. Що представляє собою схема інформаційного забезпечення САПР?
28. Що відбувається на етапі технічного проектування?
29. Що представляє собою схема інформаційних потоків в САПР?
30. Що відбувається на етапі ескізного проектування?
31. На яку інформацію, по вигляду її уявлення, може бути підрозділена інформація, що використовується при проектуванні?
32. З чого починається проектування як окремих об'єктів так і систем?
33. Що представляє собою документальна інформація?
34. Що представляє собою іконографічна інформація?
35. Дайте визначення терміну «проектна процедура» та «маршрут проектування».
36. Що представляє собою фактографічна інформація?
37. Які два види автоматизованих інформаційних систем САПР існують на сьогоднішній день?
38. На які моделі, по характеру відображення властивостей об'єкту, поділяються математичні моделі?
39. Чим забезпечується функціонування інформаційної системи?
40. На які рівні розділяються в процесі проектування, уявлення про складні технічні об'єкти?
41. Що представляють собою програмно-технічні засоби інформаційних систем?
42. Що відноситься до засобів позамашинної організації даних в інформаційних системах?
43. Що представляє собою інформаційна мова в ІПС?
44. Що представляє собою документальна інформація?
МОДУЛЬ 2. ОСНОВНІ МОЖЛИВОСТІ MATHCAD ПРИ РОЗРАХУНКУ БУДІВЕЛЬНИХ КОНСТРУКЦІЙ
лабораторна робота № 9
РОЗРАХУНОК БАЛКИ НА КОСИЙ ЗГИН
Література до теми: [1-4].
Мета роботи: Навчитись розраховувати балку на косий згин засобами Mathcad.
Завдання 9.1. Необхідно підібрати розміри поперечного перерізу дерев’яного стержня: стержень представляє собою круглу колоду, яка складається з дощок заданої товщини. Окрім навантаження та розмірів стержня задане допустиме напруження для дерева (сосна) sдоп.
Хід роботи
1.Вводимо вихідні дані. Нижче наведений фрагмент робочого документу Mathcad в якому наведені результати відповідних обчислень (див. рис. 9.1).
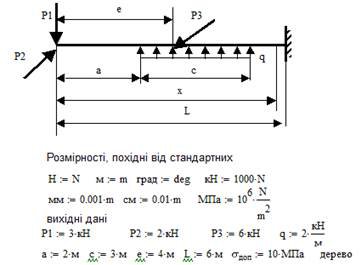
Рис. 9.1. Введення вихідних даних
2. Вводимо вирази для згинальних моментів, що діють на стержень в двох взаємно-перпендикулярних площинах, та будуємо їх епюри (див. рис. 9.2).
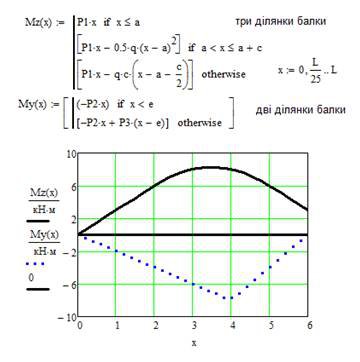
Рис. 9.2. Побудова епюр згинальних моментів в балці
3. Визначаємо розміри поперечного перерізу стержня, що складений з дощок. За умовами задачі товщина дошки та повна висота складеного перерізу - задані. Необхідно підібрати ширину перерізу з умови міцності. Невідома ширина перерізу b включена в параметри геометричних характеристик перерізу (моментів інерції J та моментів опору при згині W) та напружень s.
4. З умови міцності maxs = sдоп визначаємо ширину перерізу при різних значеннях координати x, використовуючи функцію root.
Нижче наведений фрагмент робочого документу Mathcad в якому наведені результати відповідних обчислень (див. рис. 9.3).
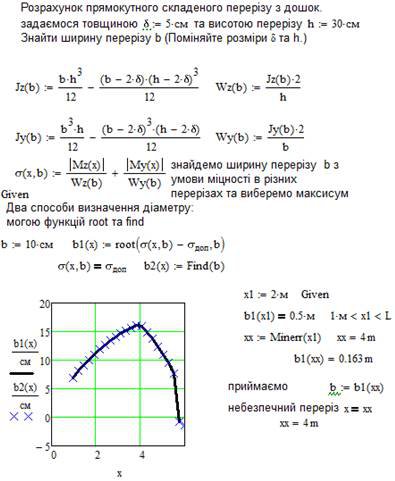
Рис. 9.3. Розрахунок прямокутного складеного перерізу з дощок
5. Визначаємо положення нейтральної вісі в небезпечному перерізі. Згідно визначенню на нейтральній вісі s = 0. Для визначення координат точок нейтральної вісі використовується функція root. Нижче наведений фрагмент робочого документу Mathcad в якому наведені результати відповідних обчислень (див. рис. 9.4).
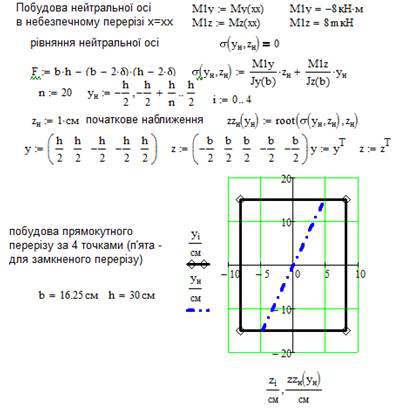
Рис. 9.4. Побудова перерізу з дощок за умовами міцності
6. Визначаємо виходячи з умов міцності діаметр круглого стержня.
Нижче наведений фрагмент робочого документу Mathcad в якому наведені результати відповідних обчислень (див. рис. 9.5).
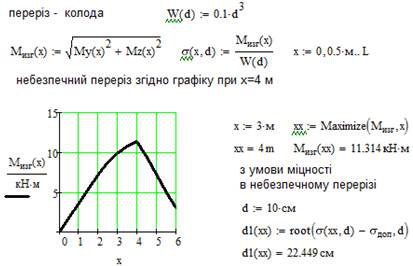
Рис. 9.5. Визначення діаметру колоди з умов міцності
Контрольні запитання:
1. Способи завдання розмірностей в Mathcad?
2. Які функції використовувались для знаходження перерізу балки за умовами міцності?
3. Яка функція використовується для знаходження небезпечного перерізу?
4. Налаштування властивостей графіків для врахування заданих розмірностей.
лабораторна робота № 10
РОЗРАХУНОК СТАТИЧНО НЕВИЗНАЧЕНОЇ РАМИ МЕТОДОМ СИЛ
Література до теми: [1-4].
Мета роботи: Навчитись розраховувати статично невизначені рами методом сил в Mathcad.
Завдання 10.1. Розрахувати пласку раму з прямолінійними та криволінійними стержнями методом сил в Mathcad.
Хід роботи
1. Вводимо вихідні дані. Всі величини взяті рівними одиниці. Нижче наведений фрагмент робочого документу Mathcad в якому наведені результати відповідних обчислень (див. рис. 10.1).

Рис. 10.1. Вихідні дані для розрахунку
2. Задану статично невизначену систему заміняємо статично визначеною та еквівалентною до заданої системи, шляхом відкидання лишніх зв’язків та заміни їх невідомими силами. Величину цих сил визначаємо з умови еквівалентності двох систем (рис. 10.2).
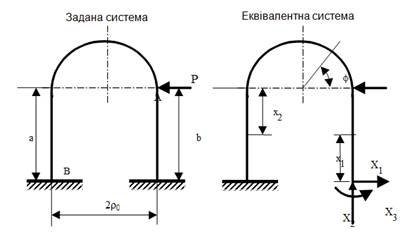
Рис. 10.2. Схеми заданої та еквівалентної систем
Схеми завантажень заданої, еквівалентної, завантаженої та одиничних систем наведені на рис. 10.3.
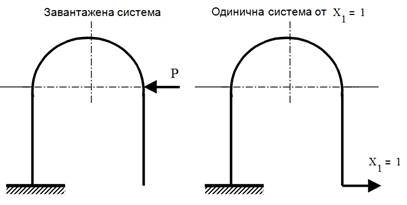
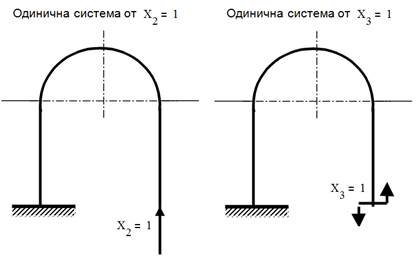
Рис. 10.3. Схема завантаження заданої та еквівалентної одиничної систем
3. Визначаємо згинальні моменти від зовнішніх та одиничних сил. Нижче наведений фрагмент робочого документу Mathcad в якому наведені результати відповідних обчислень (див. рис. 10.4).

Рис. 10.4. Згинаючі моменти від зовнішніх та одиничних сил
4. Визначаємо коефіцієнти піддатливості та розв’язуємо систему канонічних рівнянь. Нижче наведений фрагмент робочого документу Mathcad в якому наведені результати відповідних обчислень (див. рис. 10.5).

Рис. 10.5. Розв’язання системи канонічних рівнянь методом сил
5. Визначаємо кутове переміщення точки A. Нижче наведений фрагмент робочого документу Mathcad в якому наведені результати відповідних обчислень (див. рис. 10.6).
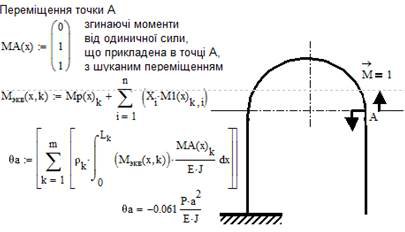
Рис. 10.6. Визначення переміщення в заданій точці
6. Перевіряємо правильність отриманого рішення. Для цього знаходимо переміщення еквівалентної системи в точках, де переміщення системи відомі заздалегідь (на опорах). В нашому випадку була відкинута права опора та методом сил були знайдені реакції в ній. Для перевірки знаходимо переміщення лівої опори B еквівалентної системи за допомогою інтегралу Мора (рис. 10.7).

Рис. 10.7. Перевірка правильності отриманого результату
Так як в жорсткому защемленні немає переміщень і всі три переміщення опори B (вертикальне, горизонтальне та кутове) дорівнюють нулю, відповідно, рішення задачі є правильним.
Контрольні запитання:
1. Для чого вбудованій змінній ORIGIN надається значення одиниці?
2. Якими засобами Mathcad визначаються згинальні моменти від зовнішніх та одиничних сил?
3. Якими засобами Mathcad розв’язується система канонічних рівняння методу сил?
4. Якими засобами Mathcad відбувається перевірка отриманих результатів?
лабораторна робота № 11
РОЗРАХУНОК ВИМУШЕНИХ КОЛИВАНЬ БАЛКИ
Література до теми: [1-5].
Мета роботи: Навчитися визначати вимушені коливання балки засобами Mathcad.
Завдання 11.1. Визначити вимушені коливання балки на двох опорах з встановленим посередині електродвигуном, що має неврівноважений вантаж на осі.
Хід роботи
1. Вводимо вихідні дані з розмірностями похідними від стандартних. Нижче наведений фрагмент робочого документу Mathcad в якому наведені результати відповідних обчислень (див. рис. 11.1).
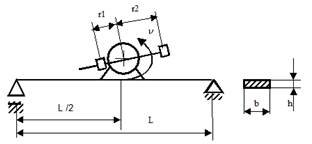

Рис. 11.1. Вихідні дані для розрахунку
2. Визначаємо власну частоту коливань балки. Для цього спочатку обчислюємо площу поперечного перерізу балки F, осьовий момент інерції J, жорсткість балки при згині K та коефіцієнт приведення маси kпр. Нижче наведений фрагмент робочого документу Mathcad в якому наведені результати відповідних обчислень (див. рис. 11.2).

Рис. 11.2. Розрахунок власної частоти коливань балки
3. Визначаємо коефіцієнт затухання коливань балки із використанням логарифмічного декременту. Нижче наведений фрагмент робочого документу Mathcad в якому наведені результати відповідних обчислень (див. рис. 11.3).
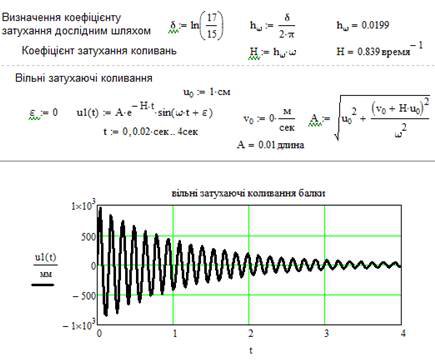
Рис. 11.3. Визначення коефіцієнта затухання коливань балки
4. Визначаємо залежність переміщення від сили та часу за допомогою інтегралу Дюамеля. Навантаження P, є вертикальною складовою відцентрової сили, що змінюється по синусоїді. В момент резонансу на протязі 3-4 секунд амплітуда коливань зростає, досягає свого максимуму та далі не змінюється.
Нижче наведений фрагмент робочого документу Mathcad в якому наведені результати відповідних обчислень (див. рис. 11.4).
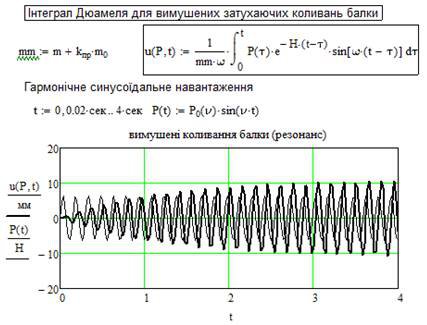
Рис. 11.4. Вимушені коливання балки
5. Визначаємо коефіцієнт динамічності, що показує у скільки разів зростає амплітуда коливань в порівнянні зі статичним прогином балки. Для знаходження максимальної амплітуди використовуємо функцію Minner. Результат обчислень залежить від обраного початкового наближення. Нижче наведений фрагмент робочого документу Mathcad в якому наведені результати відповідних обчислень (див. рис. 11.5).

Рис. 11.5. Визначення коефіцієнта динамічності
Контрольні запитання:
1. Які розмірності, похідні від стандартних використовуються в задачі?
2. Яким чином розраховувалась власна частота коливань балки?
3. В чому полягає суть визначення коефіцієнту затухання дослідним шляхом?
4. Яка функція використовувалась для знаходження максимальної амплітуди коливань балки?
лабораторна робота № 12
РОЗРАХУНОК ПРУЖНОПЛАСТИЧНОГО ЗГИНУ БАЛКИ
Література до теми: [1-4].
Мета роботи: Навчитися визначати розподіл напружень в балці при згині.
Завдання 12.1. Визначити та проаналізувати розподіл напружень в балці прямокутного перерізу від згинального моменту.
Хід роботи
1. Вводимо вихідні дані. Нижче наведений фрагмент робочого документу Mathcad в якому наведені результати відповідних обчислень (див. рис. 12.1).
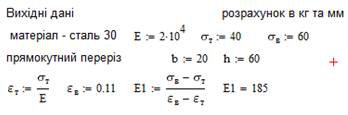
Рис. 12.1. Вихідні дані для розрахунку
Розподіл деформацій та напружень по висоті перерізу балки наведено на рис. 12.2. В даному прикладі використовуються обчислені заздалегідь апроксимації узагальненої діаграми деформування сталі.
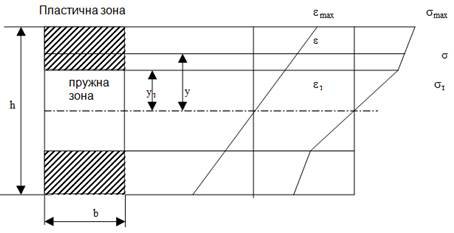
Рис. 12.2. Розподіл деформацій та напружень по висоті
2. Визначаємо згинальний момент в балці. Нижче наведений фрагмент робочого документу Mathcad в якому наведені результати відповідних обчислень (див. рис. 12.3).

Рис. 12.3. Визначення згинального моменту
3. Будуємо залежність моменту M від деформації. При використанні діаграми Прандтля (k = 1) пластичний шарнір утворюється при деформації 1%, тобто згинальний момент практично не зростає при збільшенні деформації, що відповідає yT = 6 мм (рис. 12.4).
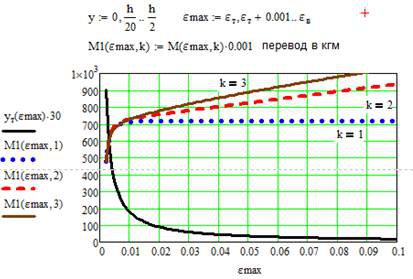
Рис. 12.4. Згинальний момент M та межа зони пластичності yT
4. За допомогою функції root для заданого навантаження визначаємо максимальну деформацію та будуємо розподіл напружень в балці.
Нижче наведений фрагмент робочого документу Mathcad в якому наведені результати відповідних обчислень (див. рис. 12.5).
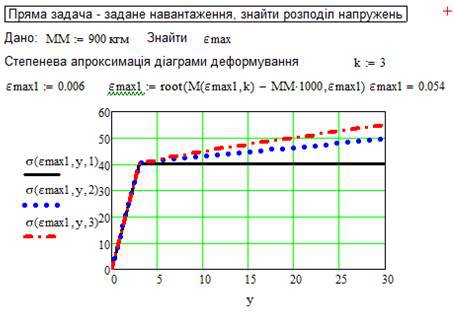
Рис. 12.5. Розподіл напружень,
що відповідає заданому навантаженню
Епюра напружень при навантаженні, напружень при розвантаженні та залишкових напружень наведені на рис. 12.6.
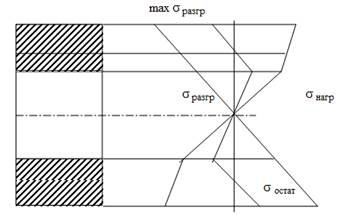
Рис. 12.6. Виникнення залишкових напружень в балці
5. Визначаємо залишкові напруження при згинальному моменті.
Нижче наведений фрагмент робочого документу Mathcad в якому наведені результати відповідних обчислень (див. рис. 12.7).
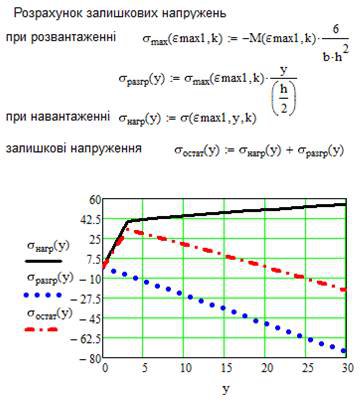
Рис. 12.7. Залишкові напруження при згині балки
Контрольні запитання:
1. Якими засобами Mathcad можна визначити напруження в балці з урахуванням апроксимації діаграми деформування?
2. Якими засобами Mathcad можна визначити зону пластичності в балці?
3. Якими засобами Mathcad можна визначити залишкові напруження в балці при згинальному моменті?
4. Використання функції root при визначенні напружень в балці від заданого навантаження?
лабораторна робота № 13
ОЦІНКА ПАРАМЕТРІВ СТАТИСТИЧНОЇ ВИБІРКИ
Література до теми: [1-4].
Мета роботи: Навчитися програмувати та обробляти об’ємні статистичні задачі в Mathcad.
Завдання 13.1. Для заданої вибірки необхідно підібрати закон розподілу та визначити його параметри.
Хід роботи
Для створення вибірки даних в лабораторній роботі використовується генератор випадкових чисел, що дозволяє створювати вибірку даних, що підпорядковані заздалегідь заданому закону розподілу.
1. Вводимо вихідні дані. Нижче наведений фрагмент робочого документу Mathcad в якому наведені результати відповідних обчислень (див. рис. 13.1).

Рис. 13.1. Створення статистичної вибірки, її параметри та перша оцінка статистичних гіпотез
В лабораторній роботі застосовуються три генератори випадкових чисел (вони виділені в рамках) для нормального rnorm, логістичного rlogis та рівномірного runif розподілу (рис. 13.1). Пересуваючи вниз один з генераторів, запускаються в розрахунок саме його дані.
2. Прийняту вибірку даних сортуємо за зростанням функцією sort для подальшої побудови графіків та визначаємо для неї середнє арифметичне mean та середньоквадратичне stdev відхилення.
3. Висуваємо три гіпотези закону розподілу та визначаємо функцію ймовірності для них. При цьому припускаємо, що вибірка даних підпорядковується: нормальному розподілу (функція ймовірності pnorm); логістичному розподілу (plogis); рівномірному розподілу (punif).
4. Будуємо графік порівняння вибірки даних xi та функцій ймовірності всіх трьох вибраних законів розподілу. Для оцінки використовуємо сумарну ймовірність pi, що дорівнює 1 для повної вибірки. Нижче наведений фрагмент робочого документу Mathcad в якому наведені результати відповідних обчислень (див. рис. 13.2).
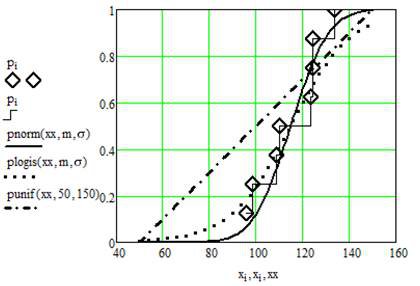
Рис. 13.2. Графічне порівняння вибірки даних
та статистичних гіпотез
5. Будуємо гістограму вибірки даних за допомогою вбудованої функції histogram, що повертає матрицю з двох стовбців. Перший з них – значення x середини інтервалів, другий – відносні частоти (стовпчики, див. рис. 13.3). На тому ж рисунку ромбиками та точками показані значення щільності ймовірності трьох розподілів, що знайдені функціями dnorm, dlogis та dunif. Нижче наведений фрагмент робочого документу Mathcad в якому наведені результати відповідних обчислень (див. рис. 13.3).
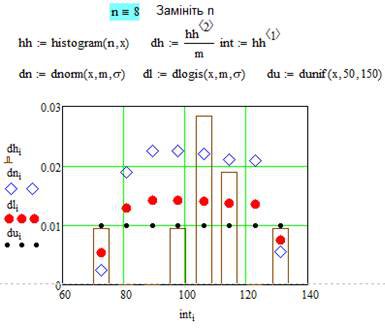
Рис. 13.3. Гістограма вибірки даних та щільності ймовірностей статистичних гіпотез
6. Оцінюємо висунуті гіпотези за допомогою критеріїв Пірсона та Романовського. Нижче наведений фрагмент робочого документу Mathcad в якому наведені результати відповідних обчислень (див. рис. 13.4).
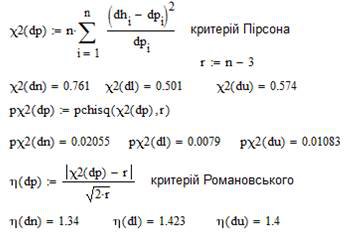
Рис. 13.4. Критерії згоди Пірсона та Романовського
7. Оцінюємо параметри обраного розподілу використовуючи метод максимальної правдоподібності. Нижче наведений фрагмент робочого документу Mathcad в якому наведені результати відповідних обчислень (див. рис. 13.4).

Рис. 13.4. Оцінка параметрів вибраного розподілу
методом максимальної правдоподібності
Контрольні запитання:
1. Які генератори випадкових чисел використовуються в даній лабораторній роботі?
2. Яка функція використовується для сортування вибірки за зростанням?
3. Які функції використовуються для визначення середнє арифметичного та середньоквадратичного відхилення?
4. Які функції ймовірності використовувались в даній лабораторній роботі?
5. За допомогою якої функції відбувалася побудова гістограми вибірки даних?
ЗАПИТАННЯ ДЛЯ МОДУЛЬНОГО КОНТРОЛЮ З МОДУЛЯ 2 “ОСНОВНІ МОЖЛИВОСТІ MATHCAD ПРИ РОЗРАХУНКУ БУДІВЕЛЬНИХ КОНСТРУКЦІЙ”
(теоретичний матеріал)
1. Дайте визначення математичному забезпеченню САПР.
2. Наведіть основні вимоги до математичного забезпечення САПР.
3. В чому полягає універсальність математичного забезпечення САПР?
4. В чому полягає алгоритмічна надійність математичного забезпечення САПР?
5. В чому полягає точність математичного забезпечення САПР?
6. Що розуміють під поняттям «витрати машинного часу» в математичному забезпеченні САПР?
7. Що розуміють під поняттям «використовувана пам'ять» в математичному забезпеченні САПР?
8. Дайте визначення поняттю «математичні моделі».
9. Які вимоги пред’являються до математичних моделей?
10. Що представляють собою структурні математичні моделі?
11. Що представляють собою функціональні математичні моделі?
12. Що представляють собою аналітичні математичні моделі?
13. Що представляють собою алгоритмічні математичні моделі?
14. Дайте визначення поняттю «повна математична модель».
15. Дайте визначення поняттю «макромодель».
16. Що представляють собою математичні моделі на мікрорівні?
17. Що представляють собою математичні моделі на макрорівні?
18. Що представляють собою математичні моделі на метарівні?
19. В чому полягає суть макромоделювання?
20. Які основні умови повинні виконуватись при макромоделюванні?
21. Основні вимоги до технічних засобів САПР?
22. Наведіть схематично структуру технічного забезпечення САПР
23. Дайте визначення поняттю «канал передачі даних».
24. Які типи мереж існують для забезпечення потреб технічного забезпечення САПР?
25. Які варіанти топології локальних обчислювальних мереж Вам відомі?
26. Дайте визначення поняттю «автоматизоване робоче місце проектувальника».
27. Що входить в склад автоматизованого робочого місця проектувальника?
28. Для яких цілей використовуються центральний обчислювальний комплекс?
29. Які режими апаратури в комплексі технічних засобів САПР Вам відомі?
30. Що розуміють під поняттям «корпоративна мережа»?
31. Що розуміють під поняттям «територіальна мережа»?
32. Наведіть схематично структуру технічного забезпечення САПР для великої організації.
33. Дайте визначення поняттю «сервер».
34. Які типи серверів Вам відомі?
35. Які варіанти конфігурацій комплексу технічних засобів САПР Вам відомі?
36. Що представляє собою пакетний режим роботи між користувачем та ЕОМ?
37. Що представляє собою діалоговий режим роботи між користувачем та ЕОМ?
38. В чому полягає суть мультипрограмного діалогового режиму роботи обчислювальної системи?
39. В чому полягає суть автономного режиму роботи обчислювальної системи?
40. В чому полягає суть режиму роботи обчислювальної системи у взаємодії з центральним обчислювальним комплексом?
41. Дайте визначення поняттю «програмне забезпечення САПР».
42. Що входить в склад програмного забезпечення САПР?
43. В чому полягає суть загальносистемного програмного забезпечення САПР?
44. В чому полягає суть спеціалізованого програмного забезпечення САПР?
45. Наведіть схематично структуру загальносистемного програмного забезпечення САПР.
46. В чому полягає суть створення пакетів прикладних програм?
47. Чим характеризуються пакети прикладних програм простої структури?
48. Чим характеризуються пакети прикладних програм складної структури?
49. Які вимоги пред’являються до програмного забезпечення САПР?
50. В чому полягає суть принципів модульності і ієрархічності програмного забезпечення САПР?
51. В чому полягає суть методичного забезпечення САПР?
52. В чому полягає суть лінгвістичного забезпечення САПР?
53. Дайте визначення поняттю «мови програмування».
54. Дайте визначення поняттю «мови проектування».
55. Дайте визначення поняттю «мови керування».
56. Які основні типи мовних процесорів Вам відомі?
57. Що розуміють під поняттям «трансляція»?
58. Наведіть схематично класифікацію основних мов програмування.
59. Наведіть схематично класифікацію основних мов проектування.
60. Що представляє собою організаційне забезпечення САПР?
Список літератури
1. Макаров Е.Г. Инженерные расчеты в Mathcad 15. Учебный курс. – СПб.: Питер, 2011, – 400с.
2. Макаров Е.Г. Mathcad: Учебный курс. – СПб.: Питер, 2009, – 384с.
3. Васильев А.Н. Mathcad 13 на примерах. – СПб.: БХВ-Петербург, 2006, – 528с.
4. Алексеев Е.Р., Чеснокова О.В. Решение задач вычислительной математики в пакетах MathCAD 12, MATLAB 7, Maple 9. – М.: НТ Пресс, 2006, – 496с.
Похожие материалы
... кта та алгоритму його функціонування, або алгоритму процесу, а також уявлення опису на різноманітних мовах здійснюється взаємодією людини і ЕОМ. Система автоматизованого проектування - це комплеск засобів автоматизації проектування, взаємозв’язаних з необхідними підрозділами проектної організації або колективом спеціалістів (користувачем системи), які виконують автоматизоване проектування. САПР ...
... програмування машин с числовим програмним керуванням (ЧПК), контроль якості і упаковку. 3. Основні поняття про системи автоматизованого виробництва САМ Автоматизоване проектування (computer-aided design — CAD) представляє собою технологію, що полягає в використанні комп’ютерних систем для полегшення створення, зміни, аналізу і оптимізації проектів. Таким чином, будь-яка програма, що ...
... . Сімейство продуктів AutoCAD є одним з найбільш поширених САПР в світі. Компанія Autodesk займається розробкою системи автоматизованого проектування AutoCAD c 1982 року, тобто більше 26 років. AutoCAD надає всі необхідні кошти для оформлення креслень: широкий набір графічних примітивів, засоби для автоматичного нанесення розмірів, штрихування, заливки, інструменти для копіювання, повороту, ...
... САЕ, окупаються значним зниженням термінів і вартості розробки. Таким чином, технології CAD, САМ і САЕ полягають в автоматизації і підвищенні ефективності конкретних стадій життєвого циклу продукту. Розвиваючись незалежно, ці системи ще не до кінця реалізували потенціал інтеграції проектування і виробництва. Для рішення цієї проблеми була запропанована нова технологія, яка називається комп’ ...
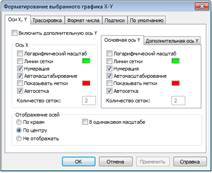
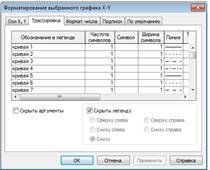
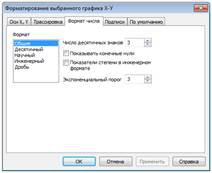
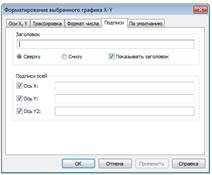
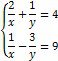
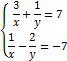
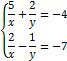
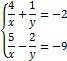
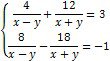
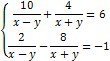
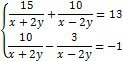
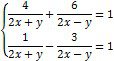
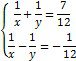
 ;
; 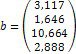
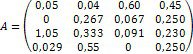 ;
; 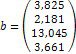
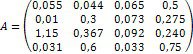 ;
; 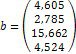
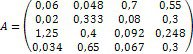 ;
; 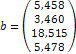
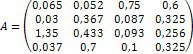 ;
; 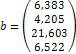
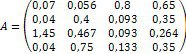 ;
; 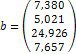
 ;
; 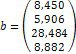
 ;
; 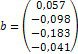
 ;
; 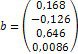
 ;
; 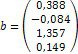
 ;
; 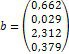
 ;
; 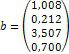
 ;
; 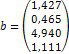
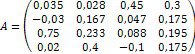 ;
; 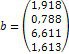
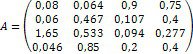 ;
; 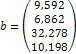
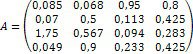 ;
; 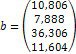
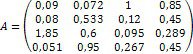 ;
; 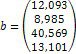
 ;
; 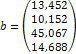




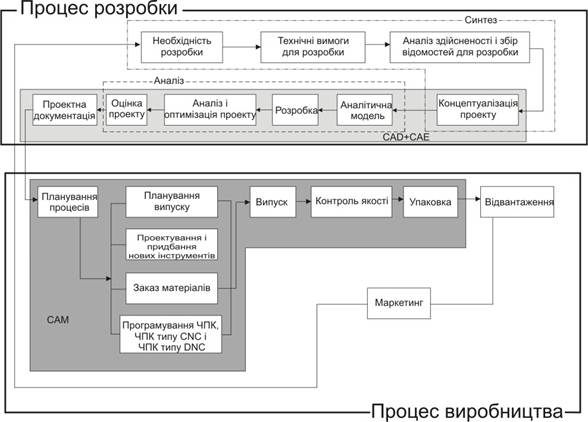
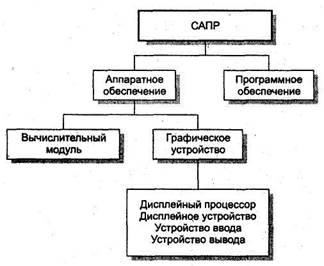
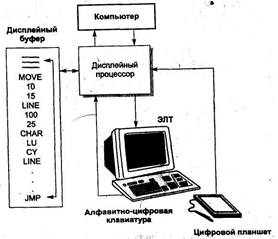
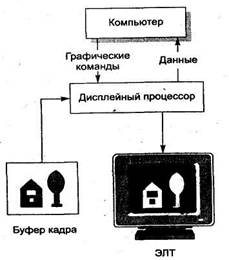
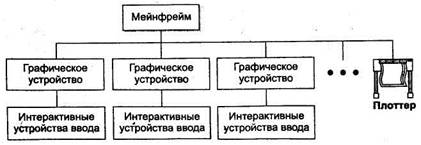
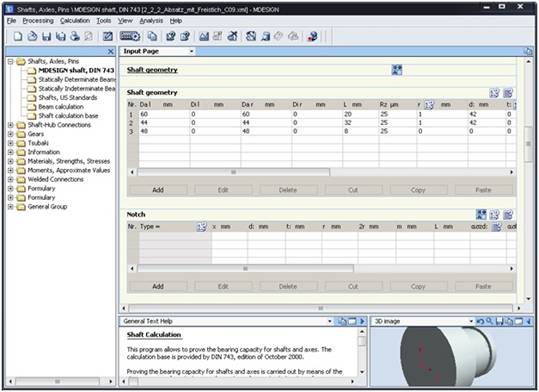
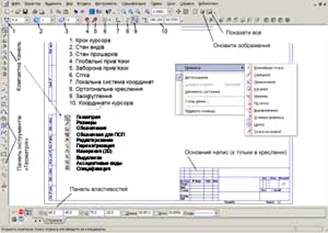
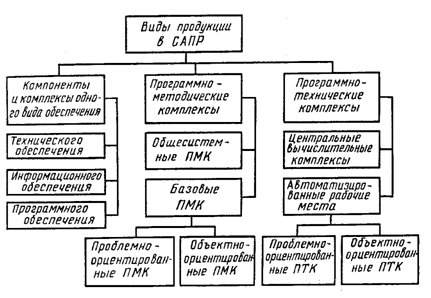
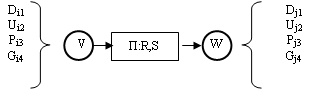
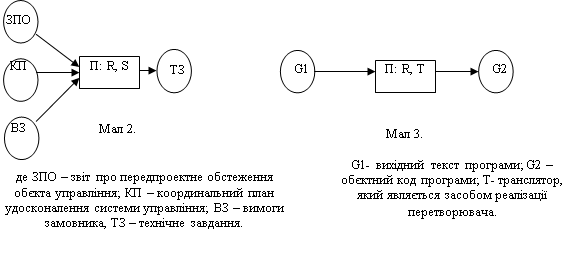
0 комментариев