МІНІСТЕРСТВО ОСВІТИ І НАУКИ
НАЦІОНАЛЬНИЙ ТРАНСПОРТНИЙ УНІВЕРСИТЕТ
КАФЕДРА ІНФОРМАЦІЙНИХ СИСТЕМИ І ТЕХНОЛОГІЇ
Курсова робота
з дисципліни «Технологія розподілених систем»
на тему:
«Реалізація базових векторно-математичних операцій в бібліотеці BLAS, ESSL, MKL»
Виконав студент: Гульшін О.В.
Група: КН-4-1
Прийняла: Ковальчук О.П.
Київ 2016
Зміст
Вступ 3
1. Теоретична частина 4
1.1 OpenMP 4
1.2 MKL 7
1.3 BLAS 13
1.4 ESSL 16
2. Практична частина 20
2.1 Приклади програми MKL 20
2.2 Приклад програми BLAS 23
2.3 Приклад програми ESSL 24
Висновки 25
Список використаної літератури 26
Вступ
Використання програмних бібліотек – це простий спосіб досягти негайного збільшення продуктивності багатоядерних, багатопроцесорних і кластерних комп'ютерних системах. Бібліотека Intel® Math Kernel Library (Intel® MKL) містить великий набір функцій, який буде корисний у додатках з великою кількістю математичних операцій. У цій роботі описується, як Intel MKL допомагає досягти прекрасною послідовної і паралельної продуктивності в звичайних додатках. Наведений матеріал застосовний до систем на процесорах IA-32 і Intel® 64 з операційними системами Windows, Linux*, і Mac OS* X.
Оптимальна продуктивність у сучасних багатопроцесорних і багатоядерних системах досягається тільки тоді, коли використовуються всі можливості паралелізму та враховуються особливості пристрою пам'яті. Для досягнення оптимальної продуктивності послідовний код повинен широко спиратися на паралелізм рівня SIMD команд і регістрів, а також використання кеш-блокинга. У паралельних програмах застосовують розвинуті стратегії угруповання даних у блоки для більш ефективного використання множинних ядер і процесорів і рівномірного розподілу паралельних завдань. У деяких випадках для складних завдань, які не поміщаються в пам'яті, можуть бути використані зовнішні (out-of-core) реалізації.
Один з найпростіших способів застосувати паралелізм у додатку з інтенсивними математичними розрахунками – використовувати багатопотокову оптимізовану бібліотеку. Це не тільки допоможе заощадити час розробки, але також і суттєво зменшить обсяг тестування. Застосування стандартизованих API робить код більш стерпним.
Теоретична частина
OpenMP
Короткий опис OpenMP
Для розпаралелювання в моделі загальної пам'яті найбільш ефективним вважається механізм ниток. Існує два протилежних підходи для використання цього механізму:
1) автоматичне розпаралелювання компілятором (недоліки: недостатня ефективність за існуючих обмежень компіляторів);
2) повністю «ручне» додавання команд звернення до бібліотеки ниток (недоліки: необхідність залучення системного пропрограмування, непереносимість між платформами).
«Золота середина» – додавання спеціальних директив підказок компілятору про розпаралелюванні. До появи OpenMP багато виробників компіляторів підопічні підтримували подібні набори директив, однак ці механізми були неповні і несумісні між собою. На цьому тлі, при підтримці великої кількості виробників компіляторів і обчислювальних систем, був створений стандарт OpenMP.
Модель виконання програм, що використовують інтерфейс OpenMP
Паралельні програми, що використовують інтерфейс OpenMP, виконуються в моделі породження паралельних ниток і очікування завершення їх виконання. Програма починає виконання як один послідовний процес, званий основний ниткою виконання. Основна нитка виконується послідовно доти, поки не зустрінеться перша конструкція розпаралелювання. Пара директив PARALLEL і END PARALLEL становить конструкцію распараллелювания і визначає паралельну область програми. Як тільки зустрічається конструкція розпаралелювання, основна нитка створює групу ниток і основна нитка стає основною ниткою групи. Оператори програми, ув'язнені в конструкцію распараллелювання, включаючи і виклики процедур, що виконуються паралельно кожної ниткою групи. По завершенні конструкції розпаралелювання нитки в групі синхронізуються, і тільки основна нитка продовжує виконання. В одній програмі може бути специфіковано будь-яке число конструкцій розпаралелювання. В результаті програма може багато разів розпаралелюватися і синхронізуватися протягом виконання. Інтерфейс OpenMP дозволяє програмісту використовувати директиви в процедурах, що викликаються зсередини конструкцій розпаралелювання. З цією функціональною можливістю користувачі можуть програмувати конструкції розпаралелювання з верхніх рівнів дерева викликів в програмі і використовувати директиви для контролю виконання в будь-який викликається процедурою. Основні визначення та поняття Програма, що використовує інтерфейс OpenMP, містить спеціальні директиви, які компілятором, що не підтримує OpenMP, будуть сприйматися як коментарі.
Директиви – це спеціальні коментарі в синтаксисі мовипрограмування Фортран, які ідентифікуються унікальною сигнальної міткою. Мітка директиви структурована так, що дирекактиви трактуються як коментарі. Компілятори, які підтримують інтерфейс OpenMP, включають можливість активізувати і дозволяти інтерпретацію всіх директив інтерфейсу OpenMP в командному рядку. Формат директив інтерфейсу OpenMP наступний:
мітка директива [клаузами [[,] клаузами] ...], мітка – послідовність символів x$OMP, клаузами задає параметри директиви.
Фактори, що впливають на продуктивність моделі загальної пам'яті з використанням інтерфейсу OpenMP:
• час на організацію і завершення ниток (заклад локальних змінних, установлення початкових даних, накопичення змінних, перелічених у клаузе REDUCTION тощо);
• очікування у критичних секціях;
• операції, що вимагають синхронізації;
• «послідовні» цикли (паралельні цикли, при описі яких використовувалася клаузами ORDER);
• робота із зовнішніми пристроями (висновок на екран тощо);
• затримки при одночасному зверненні на читання кількома нитками до одній комірці пам'яті.
MKL
Intel MKL надає великий набір математичних функцій, розпаралелених і оптимізованих для використання на нових процесорах Intel®. При першому виклику функції бібліотеки відбувається перевірка апаратних можливостей системи, в якій запущена програма. На основі даних перевірки вибирається варіант коду, який дає максимально ефективне використання паралелізму SIMD команд і регістрів, вибирається найкраща стратегія кеш-блокинга. Бібліотека Intel MKL є потокобезопасной, що означає, що її функції будуть коректно працювати при одночасному виклику з декількох потоків.
Бібліотека Intel MKL зібрана з допомогою компілятора Intel® C++ та Fortran і распараллелена через OpenMP. Її алгоритми сконструйовані таким чином, щоб дотримувався баланс даних і завдань і ефективно використовувалися ресурси процесорів. У наведеній таблиці показано розділи математики, для яких є розпаралелені функції:
1. Лінійна алгебра.
Використовується в різних програмах від аналізу методом кінцевих елементів до сучасних анімацій.
2. BLAS (Basic Linear Algebra Subprograms)
Всі операції матриця-матриця (рівень 3) распараллелены як для щільних, так і для розріджених об'єктів. Багато операції вектор-вектор (рівень 1) і матриця-вектор (рівень 2) распараллелены для щільних матриць при роботі 64-розрядний програмах на архітектурі Intel® 64. У разі розріджених матриць, распараллелены всі операції другого рівня, за винятком розріджених трикутних решателей.
3. LAPACK (Linear Algebra Package)
Кілька функцій распараллелены для наступних типів завдань: рішення лінійних рівнянь, ортогональная факторизація, сингулярне розкладання, симетричні задачі власних значень. LAPACK також використовує функції BLAS, так що навіть не розпаралелені функції можуть працювати паралельно.
4. ScaLAPACK (Scalable LAPACK)
Паралельна версія LAPACK з розподіленою пам'яттю, призначена для кластерних систем.
5. PARDISO
У цьому паралельному прямому розрідженому решателе распараллелены всі три етапи: перерозподіл (опціонально), факторизація і рішення (при вирішенні із множинними правими частинами).
6. Швидкі перетворення Фур'є.
Використовуються для обробки сигналів і в різноманітних додатках від розвідки нафти до медицини.
7. Розпаралелені ШПФ.
Распараллелены всі функції, за винятком одновимірних масивів дійсних чисел і спліт-комплексних ШПФ.
8. Кластерні ШПФ.
Паралельні ШПФ з розподіленою пам'яттю, призначені для кластерних систем.
9. Векторна математика.
Використовується у фінансових додатках.
10. Бібліотека векторної математики.
Арифметика, тригонометрія, експоненти, логарифми, округлення і т. д.
Оскільки при створенні та управлінні потоками виникають деякі витрати, не завжди вигідно використовувати багатопоточність. З цієї причини Intel MKL не створює потоки для дрібних завдань. Розмір, який вважається дрібним, оцінюється по відношенню до розділу математики і типом функції. Для BLAS третього рівня потоки підключаються при розмірності 20, в той час як BLAS першого рівня і векторні функції не параллелятся для векторів розмірністю менше 1000.
Intel MKL буде працювати на одному потоці в разі виклику з распараллеленного програми, щоб уникнути такого явища, як oversubscription. Для додатків, розпаралелених з допомогою OpenMP, це відбувається автоматично. Якщо для створення паралельності використовуються інші засоби, то поведінка Intel MKL слід регулювати за допомогою методів, описаних нижче. Для випадку, коли функції бібліотеки викликаються в послідовному режимі з декількох потоків, Intel MKL має кілька корисних функцій. Наприклад, бібліотека Vector Statistical Library (VSL) надає набір векторизованих генераторів випадкових чисел, які не распараллелены, але які мають можливість розділяти послідовність випадкових чисел між потоками програми. Функція SkipAheadStream() поділяє послідовність випадкових чисел на окремі блоки, по одному на потік. Функція LeapFrogStream() поділяє послідовність випадкових чисел таким чином, що кожен потік отримує підпослідовність початкової послідовності. Наприклад, щоб розділити послідовність між двома потоками за методом чехарди (Leapfrog), то всі числа з парними індексами призначаються одному потоку, а з непарними – іншому.
Продуктивність
На рис. 1 показаний приклад продуктивності, яку користувач може очікувати від DGEMM – функції множення двох матриць подвійної точності, яка включена в Intel MKL. Функції BLAS грають важливу роль у роботі багатьох додатків. Графік показує продуктивність в Gflops для різних розмірів матриць. Показано, що продуктивність зростає зі збільшенням кількості процесорів (прискорення до 1,9 х на двох потоках, 3,8 х на чотирьох і 7,9 х на восьми), досягаючи 94,3% пікової продуктивності при 96,5 Gflops.
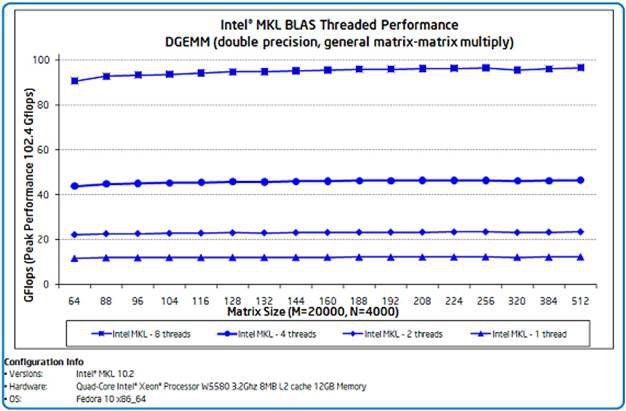
Рис. 1. Продуктивність і масштабованість функції множення матриць BLAS.
Застосування
Оскільки бібліотека Intel MKL распараллелена з використанням OpenMP, то її поведінку можна контролювати за допомогою того ж OpenMP. Для додаткового контролю за поведінкою потоків в Intel MKL є кілька сервісних функцій, які дублюють контрольні функції OpenMP. Ці функції дозволяють контролювати кількість використовуваних бібліотекою потоків, як в цілому, так і в залежності від розділу (тобто окремо для BLAS, LAPACK тощо). Такі незалежні контрольні функції можна застосовувати, наприклад, для вкладення паралелізму. Поведінку програми, распараллеленного з допомогою OpenMP, можна контролювати за допомогою змінної оточення OMP_NUM_THREADS або функції omp_set_num_threads(), в той час як поведінка потоків Intel MKL незалежно встановлюється через власні змінну і функцію MKL_NUM_THREADS і mkl_set_num_threads(). Нарешті, для тих, кому завжди треба запускати функції Intel MKL тільки на одному потоці, існує послідовна версія бібліотеки, абсолютно незалежна від распараллеливающей бібліотеки.
Бібліотека Intel MKL добре оптимізована для паралельної роботи на кластерних установках, мають на вузлах багатоядерні процесори з прискорювачами Intel Xeon Phi, і на SMP-системах (системах зі спільною пам'яттю). Бібліотека підтримує як гетерогенний режим обчислень, коли код бібліотеки виконується одночасно на хост-процесорі вузла і на прискорювачі (сопроцессоре), так і однорідний режим обчислень, коли код бібліотеки виконується одночасно тільки на сопроцессорах або тільки на хост-процесорах. Для використання бібліотеки Intel MKL додаток може бути зібрано компілятором
Intel з зазначенням опції «mkl».
Доступні три способи (режими) використання математичної бібліотеки Intel MKL:
· Automatic Offload mode – буквально «автоматичне вивантаження», використовується при гетерогенном режимі обчислень;
· Offload mode supported by Compiler – вивантаження з підтримкою від компілятора; у цьому режимі процес вивантаження (перенесення частини обчислень) обчислювального коду на прискорювач задається в програмі за допомогою директив компілятора;
· Native mode – код бібліотеки виконується одночасно тільки на прискорювачах (сопроцессорах).
Технологія Intel® Hyper-Threading найбільше ефективна тоді, коли всі потоки виконують різні типи операцій і в процесорі присутні неповних ресурси. Однак Intel MKL не відповідає цим умовам, оскільки паралельна частина бібліотеки використовує більшу частину ресурсів і в кожному потоці виконуються ідентичні операції. З цієї причини Intel MKL за замовчуванням використовує кількість потоків дорівнює кількості фізичних ядер.
BLAS
Основні операції з векторами і матрицями:
- BLAS (базові підпрограми лінійної алгебри);
- SparseBLAS (Базові Підпрограми Лінійної Алгебри);
- PBLAS (паралельні BLAS).
Basic Linear Algebra Subprograms (BLAS) - встановлений де-факто стандарт інтерфейсу бібліотек підпрограм, призначених для виконання основних операцій лінійної алгебри, таких як, наприклад, множення матриць та векторів. Уперше такі підпрограми було опубліковано 1979 року. На їх основі будуються більші пакети, такі як LAPACK. Конкретні втілення протоколу у вигляді бібліотек розробляються як провідними лідерами комп'ютерної технології, наприклад, Intelом, так і іншими авторами. Підпрограми лінійної алгебри широко використовуються в застосуваннях, які вимагають інтенсивних обчислень, а тому вимагають особливо уважної розробки й оптимізації. Наприклад, ATLAS - варіант BLAS, який може легко переноситися з однієї платформи на іншу й оптимізуватися для використання на машинах конкретної архітектури.
Бенчмарк LINPACK сильно залежить від швидкості виконання підпрограми DGEMM, яка входить до BLAS.
Функціональність BLAS розбивається на три рівні
Рівень 1
Цей рівень містить операції загального вигляду
y← αx+y
а також скалярного добутку, норми вектора та деякі інші.
Рівень 2
Цей рівень містить операції дій між векторами й матрицями загального вигляду
y← αAx+βy
а також підпрограми знаходження розв'язку рівняння Tx= y для трикутної матриці T.
Рівень 3
Цей рівень містить операції з матрицями вигляду
C←αAB+ βC
а також розв'язок рівняння B←αT-1B для трикутної матриці T та інші підпрограми. Зокрема сюди входить популярна у використаннях операція перемноження матриць.
SparseBLAS – розширення BLAS для роботи з розрідженими векторами і матрицями.
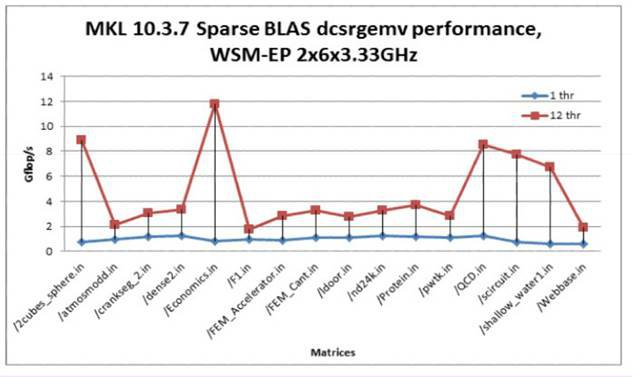
Рис.2. Продуктивність SparseBLAS.
PBLAS – паралельна реалізація BLAS для обчислювальних пам'яттю. Побудована на основі MPI.
Формати зберігання матриць:
- щільний – матриця зберігається в двовимірному масиві;
- упакований – використовується для симетричних або трикутних матриць. Елементи матриці зберігаються послідовно, по стовпцях;
- стрічковий - використовується для стрічкових матриць. Двовимірний масив зберігає діагоналі матриці.
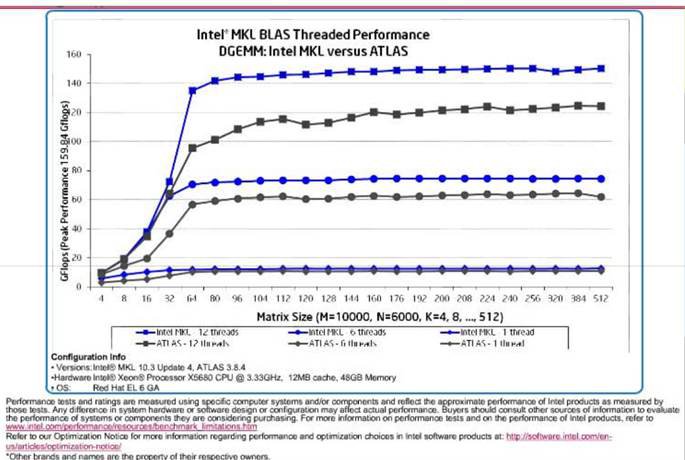
Рис. 3. BLAS.
ESSL
ESSL і Parallel ESSL збірники впроваджений математичних підпрограм, спеціально розроблених для підвищення ефективності інженерних і наукових додатків на базі процесорів POWER™ серверів і блейд-IBM. ESSL і паралельний ESSL зазвичай використовуються в аерокосмічній, автомобільній, електронній, нафтової, комунальних послуг і науково-дослідних галузей для таких додатків, як:
1. Структурний аналіз
2. Аналіз часових рядів
3. Обчислювальна хімія
4. Обчислювальні методи
5. Гідродинаміка аналіз
6. Математичний аналіз
7. сейсмічний аналіз
8. Динамічні системи моделювання
9. Водосховище Моделювання
10. ядерна техніка
11. Кількісний аналіз
12. Електронна Circuit Design
ESSL і паралельна підтримка ESSL 32-розрядні і 64-розрядні Fortran, C та C ++ серійний, SMP і SPMD додатків, що працюють під AIX® Linux®.
ESSL
ESSL являє собою набір високопродуктивних математичних підпрограм, які забезпечують широкий спектр функцій для багатьох спільних наукових та інженерних додатків. Математичні підпрограми розділені на дев'ять обчислювальних областях:
1. Лінійна алгебра Підпрограми
2. Матричні операції
3. Лінійних алгебраїчних рівнянь
4. Аналіз Eigensystem
5. Перетворення Фур'є, згорток, Кореляції та обчислення, пов'язані з
6. Сортування і пошук
7. інтерполювання
8. чисельна квадратура
9. Генератор випадкових чисел
ESSL надає наступні бібліотеки часу виконання:
- Serial Library ESSL надає поточно-версії ESSL підпрограм для використання на всіх процесорах. Ви можете використовувати цю бібліотеку для розробки власних багатопоточних додатків.
- (SMP) Бібліотека ESSL Symmetric Multi-Processing забезпечує поточно-версії ESSL підпрограм для використання на всіх процесорах SMP. Крім того, деякі з цих підпрограм також багатопотокова, сенс, вони підтримують паралельну обробку моделі програмування використовується спільно з пам'яттю. Вам не потрібно змінювати існуючі прикладні програми, які вимагають ESSL, щоб скористатися перевагами підвищеної продуктивності з використанням процесорів SMP; ви можете просто повторно пов'язати існуючі програми.
Serial Library ESSL і ПКМ бібліотека ESSL підтримує наступні операційні системи програм:
- 32-розрядні цілі числа і 32-розрядні покажчики
- 32-розрядні цілі числа і 64-розрядні покажчики
- 64-розрядні цілі числа і 64-розрядні покажчики
Всі бібліотеки покликані забезпечити високий рівень продуктивності для чисельно інтенсивних обчислювальних робіт і обидва забезпечують математично еквівалентні результати. У ESSL Підпрограми можуть бути викликані з прикладних програм, написаних на мові Fortran, C та C ++. ESSL працює на операційних системах AIX і Linux.
Паралельний ESSL
Паралельний ESSL є масштабованим математична бібліотека підпрограм для автономних кластерів або кластерів серверів, підключених через комутатор і під управлінням AIX і Linux. Паралельний ESSL підтримує модель програмування єдиної програми Кілька даних (СПМД) з використанням бібліотеки Message Passing Interface (MPI). Паралельні бібліотеки ESSL SMP підтримують паралельні програми для обробки на кластери серверів Power Systems і лез, з'єднаних за допомогою опорної IP локальної мережі або за допомогою перемикача InfiniBand.
Паралельний ESSL забезпечує підпрограми в наступних областях обчислювальних:
- Рівень 2 Паралельний Основні лінійної алгебри Підпрограми (PBLAS)
- Рівень 3 PBLAS
- Лінійних алгебраїчних рівнянь
- Eigensystem аналіз і сингулярні вартісний аналіз
- Перетворення Фур'є
- Генератор випадкових чисел
Для зв'язку, паралельний ESSL включає в себе основні функції лінійної алгебри Підпрограми Communications (BLACS), які використовують MPI. Для обчислень, Паралельний ESSL використовує ESSL підпрограм (ESSL є попередньою умовою).
Паралельні ESSL підпрограми можуть бути викликані з 32-бітних і 64-розрядних прикладних програм, написаних на Fortran, C і C++, що працює під управлінням операційної системи AIX і Linux.
Паралельні ESSL SMP бібліотеки призначені для використання з паралельною бібліотеки IBM MPI Environment. Ви можете запустити один або багатопотоковий IP-додатків в США або на всіх типах вузлів. Тим не менш, ви не можете одночасно зателефонувати паралельний ESSL з декількох потоків.
Практична частина
Приклад програми MKL
Вирішити одновимірне рівняння теплопровідності методом кінцевих різниць.
Самостійно розібрати процедури:
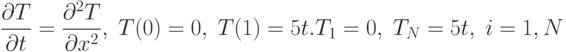
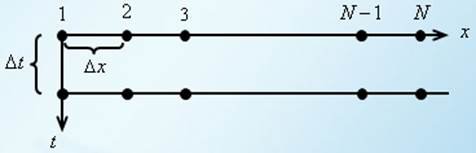
Приклад
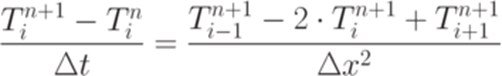
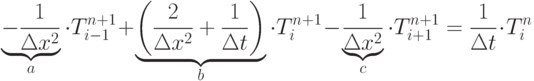
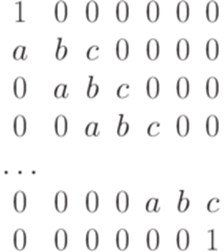
Варіант програми №1
program teplo_1D
use lapack95
use f95_precision
integer, parameter :: N = 64
integer k
real DL(N-1), D(N), DU(N-1) ! DL - нижняя, D - основная, DU - верхняя
real AB(4,N)
real :: UN(N) = 0
real :: dt = 0.01 ! --- шаг по времени
real, parameter :: H = 1.0 ! --- длина области
real :: dh = H/(N-1) ! шаг по области
integer IPIV(N), INFO
!==========================================================
open(1,file = "res1.txt")
open(3,file = "res2.txt")
open(5,file = "res3.txt")
!------ заполняем диагонали
!------ так как на границах Г.У. первого рода
DL = -dt/dh**2; DL(N-1) = 0 ! --- нижняя
D = 2*dt/dh**2+1; D(1) = 1; D(N) = 1 ! --- основная
DU = -dt/dh**2; DU(1) = 0 ! --- верхняя
Варіант програми №2
!----- формируем AB-матрицу AB(1,:) = 0 ! не заполняем, нужна для процедур AB(2,2:N) = DU AB(3,1:N) = D AB(4,1:N-1) = DL call gbtrf(AB, ipiv = IPIV) ! ---- делаем факторизацию do k = 1,500 UN(N) = 5*k*dt ! ----- правая часть call gbtrs(AB, UN, IPIV, info = INFO) ! --- вызываем решатель if ((k == 100).OR.(k == 300).OR.(k == 500)) then do i = 1,N x = (i-1)*dh write(k/100,*) x, UN(i) end do close(k/100) end if end do close(1) close(3) close(5) endПриклад програми BLAS
Приклад програми множення двох матриць з використанням BLAS:
#include<stdio.h>
#include<cblas.h> // заголовочный файл C-интерфейса библиотеки BLAS
#define M 300
#define N 400
#define K 500
int main()
{ int i,j;
float A[M*K], // массив расположен в памяти одним непрерывным блоком
B[K][N], // этот тоже
*C; // и этот тоже будет непрерывным
C=(float*)malloc(M*N*sizeof(float)); // ну вот, непрерывный ;)
for (i=0;i<M;i++) // инициализируем массив A
for (j=0;j<K;j++)
A[i*K+j]=3*j+2*i;
for (i=0;i<K;i++) // инициализируем массив B
for (j=0;j<N;j++)
B[i][j]=5*i+j;
for (i=0;i<M*N;i++) C[i]=5; // инициализируем массив C (зачем?)
// перемножаем!!!
// нам нужно C=AB, поэтому сделаем beta=0
cblas_sgemm(CblasRowMajor,CblasNoTrans,CblasNoTrans,
M,N,K,1.0,A,K,&B[0][0],N,0.0,C,N);
for (i=0;i<M;i++) // выводим результат на экран (наверно не влезет: 300*400)
{ for (j=0;j<N;j++) printf("%.2f ",C[i*N+j]);
printf("\n");
}
free(C);
return 0;
}
Приклад програми ESSLУ прикладі програми наступні дев'ять рядків коду на мові FORTRAN:
do l=1,control
do j=1,control
xmult=0.d0
do k=1,control
xmult=xmult+a(i,k)*a(k,j)
end do
b(i,j)=xmult
end do
end do
Висновки
У цій роботі розглядалося і було доведено, що використання програмних бібліотек – це простий спосіб досягти негайного збільшення продуктивності багатоядерних, багатопроцесорних і кластерних комп'ютерних системах. Бібліотека Intel® Math Kernel Library (Intel® MKL) містить великий набір функцій, який буде корисний у додатках з великою кількістю математичних операцій. Наведений матеріал застосовний до систем на процесорах IA-32 і Intel® 64 з операційними системами Windows, Linux*, і Mac OS* X.
Отже, один з найпростіших способів застосувати паралелізм у додатку з інтенсивними математичними розрахунками – використовувати багатопотокову оптимізовану бібліотеку. Це не тільки допоможе заощадити час розробки, але також і суттєво зменшить обсяг тестування.
Список використаної літератури:
1. Бекон, Д. Операционные системы / Бекон Д., Харрис Т.; пер. с англ. –
Спб.: Питер; Киев: Издательская группа BHV, 2004 – 800 с.
2. Вальковский, В.А. Распараллеливание алгоритмов и программ.
Структурный подход / Вальковский В.А. – М.: Радио и связь, 1989. – 176 с.
3. Воеводин, В.В. Параллельные вычисления / Воеводин В.В., Воеводин Вл.В. – СПб.: БХВ-Петербург, 2002. – 608 с.
4. Гергель, В.П. Основы параллельных вычислений для многопроцессорных вычислительных систем. Учебное пособие / Гергель В.П., Стронгин Р.Г. – Нижний Новгород: Изд-во ННГУ, 2003. – 184 с.
5. Кейслер, С. Проектирование операционных систем для малых ЭВМ.
/ С. Кейслер; пер. с англ. – М.: Мир, 1986. – 680 с.
6. Корнеев, В.Д. Параллельное программирование в MPI / Корнеев В.Д.
– Новосибирск: Изд-во СО РАН, 2000. – 213 с.
7. Немнюгин, С.А. Параллельное программирование для многопроцессорных вычислительных систем / Немнюгин С.А., Стесик О.Л. – СПб.: БХВПетербург, 2002. – 400с.
8. Ортега, Дж. Введение в параллельнные и векторные методы решения
линейных систем / Ортега Дж.; пер. с англ. – М.: Мир, 1991. – 367 с.
9. Программа дисциплины "Параллельные системы и параллельные
вычисления"
0 комментариев