Министерство образования республики Бурятия
Бурятский государственный университет
Колледж информационных технологий
Состязания по информатике в школе (олимпиады)(Реферат)
Выполнил: Павлов А.И.
Проверил: Цыбикова Т. С.
Улан-Удэ
2002
Оглавление
Проблемы олимпиад по информатике. 3
Постановка проблем методами наложения ограничений. 3
Ограничения на использование готовых средств. 5
Ограничения на «программирование». 6
Проведение олимпиад по информатике на основе тестов. 8
Тестовые вопросы олимпиады по информатике для старшей возрастной группы (X-XI классы) 9
Заключение. 16
Литература. 17
Проблемы олимпиад по информатике
При проведении олимпиад по информатике различного уровня в течение длительного периода времени выявился целый ряд отрицательных моментов, связанных как с организацией самих олимпиад, так и с преподаванием информатики в школах. Приведем здесь некоторые из них.
1. Нередко отмечается «запущенность» некоторых участников олимпиад: их образование и развитие происходит стихийно, и иногда им даже незнакома часть материала школьного курса информатики. Эта стихийность проявляется в замысловатых приемах типа ELSE NEXT или даже ELSE DIM на фоне незнания типовых методов решения задач. При решении простых задач такие школьники демонстрируют особо изощренные и сомнительные «трюки», но перед более трудной задачей становятся в тупик. Их внимание направлено не на алгоритмизацию как особый вид человеческого мышления и деятельности, не на постановку и решение задач, а на язык программирования (часто — доступную версию Бейсика). Но отметим их интуитивную тягу к иным, нестандартным путям решения задач.
2. По мере исчерпания тематики задач, распространения профессиональных ПЭВМ, мощных языков наметилась тенденция к решению на олимпиадах громоздких задач. Тексты к ним тоже громоздки. Проверяющие не успевают взглянуть на решения и «гонят» тесты. А в них, особенно если частные случаи очевидны, «хитрец» может написать:
ЕСЛИ N = I то ОТВЕТ := 1
ЕСЛИ N = 2 то ОТВЕТ := 3
ЕСЛИ N = 9 то ...
(авось угадаю пару тестов)
3. Быстродействие различных языковых трансляторов, не говоря уже о различных типах школьной ВТ, существенно различается. Поэтому единое ограничение по времени на тесты ведет к дискриминации, например, участника, работающего на «Корвете», По сравнению с тем, кто имеет доступ к ППЭВМ.
4. Возможности языков также сильно отличаются. Например, удобства процедур в Паскале и в «старом» Бейсике несопоставимы — и снова неравенство шансов.
Постановка проблем методами наложения ограниченийПо отношению к школьникам цели олимпиады две: выявить и способности, и образованность. Сформулируем их более точно:
1. Выявить школьников с развитыми способностями к логико-алгоритмическому мышлению. Неразвитость этого мышления может быть замаскирована использованием мощных готовых программных средств или библиотек мощного языка. Так, команда SORT в среде DBASE позволяет вообще не уметь составлять алгоритмы сортировки. Возможно, этим объясняется такой парадокс: школьники, знающие Турбо Паскаль, нередко хуже решают небольшие «хитрые» задачи, чем те, кто работает на вильнюсском Бейсике. Борьба с этим Бейсиком — хорошая школа выживания.
2. Выявить школьников образованные, с развитым системно-комбинаторным мышлением, что должно проявляться в умении использовать не только по назначению, но и оригинально, нестандартно, творчески разнообразные готовые программные средства и команды и уметь избегать программирования. Отсутствие такого стиля мышления и образованности, кругозора может быть замаскировано высоким уровнем техники «голого» программирования.
В основе предлагаемой нами концепции лежит предположение о том, что в сущности своей умственная деятельность и пользователя готовых ПС, и программиста однотипна и не зависит от мощности ВТ и ПС.
Целью этой деятельности всегда является приведение компьютерной среды в желаемое состояние при ограниченных средствах: конечное число команд и реализованных алгоритмов и функций, имеющиеся в наличии память и время. Новые поколения ЭВМ и языков программирования лишь снимают старые ограничения, но человек неизбежно наталкивается на новые.
Основной идеей предлагаемой концепции является то, что именно при преодолении ограничений не только проявляются творческие способности, но и, более того, происходит развитие человека. Так, ограниченность возможностей когтей и зубов древнего человека привела к появлению кремниевых ножей.
Попытаемся изложить смысл нашей концепции на примере спорта, где ограничения возникли давно и не являются чем-то диковинным, а составляют неотъемлемую часть всех соревнований: прыгуны в высоту не используют стремянку, штангисты — рычаги, марафонцы — велосипеды. Как пример постановки проблемы в спорте методом «искусственных» ограничений представим следующую ситуацию: перед началом велогонок у всех велосипедов удалены передние колеса.
Конечно, участник может сесть в рейсовый автобус (запрещенное средство). Он может и пойти пешком (в информатике — обойтись без ЭВМ). Но нас сейчас интересуют только те, кто сумеет:
1) отремонтировать велосипед, изготовив недостающие части из подручного материала (написать процедуры, расширяющие «зауженный» ограничениями язык);
2) проехать это расстояние на одном колесе, ничего не изобретая и не конструируя (нестандартно использовать имеющиеся средство);
3) вообще изобрести и изготовить новый велосипед (неожиданно для судей). Возвращаясь к информатике, отметим, что самая тривиальная задача может стать необычайно трудной, если условие дополнить рядом ограничений на используемые средства.
Такой прием порождения задач не только сильно упрощает условия, но и облегчает контроль. Но теперь при проверке нужно внимательно просмотреть и листинг. Это вообще поучительно для члена жюри любого уровня, но пока делалось, к сожалению, редко: надо было успеть протестировать задачи.
При введении ограничений важны уровень и полнота их системы: слишком сильные ограничения сделают задачу неразрешимой; слишком слабые — тривиальной, нетворческой; неполная система ограничений дает возможность найти «лазейку» — «законно» воспользоваться «незаконным» приемом (в нашем примере — уцепиться за бампер автобуса).
Ограничения на использование готовых средствПризнаком способностей к алгоритмизации мы полагаем умение обходиться малыми средствами, но комбинировать их свободно, расширяя свой арсенал, в сущности — язык.
Поэтому вместо очередной дискуссии о том, «чей» язык лучше, предлагаются ограничения, которые, во-первых, выравнивают условия для участников, а во-вторых, сами по себе являются источником задач, в том числе и олимпиадных. Так, например, при любом языке реализации можно запретить:
1) GOTO и любые команды циклов (FOR, WHILE, REPEAT, заодно «пострадают» и команды типа REPLACE .. FOR из сред DBASE);
2) все функции и процедуры с параметрами, кроме ввода-вывода;
3) ассемблер, машинные команды (во избежание обхода «снизу»);
4) непосредственное обращение к памяти (PEEK, MEM и др.).
Этим выравниваются возможности процедурных языков. Остаются рекурсия без параметров и условные команды. Этого достаточно для реализации любой конструкции языка. Кроме того, это сближает возможности обычных языков программирования с «насквозь» рекурсивными средствами алгоритмизации для исполнителей проекта «Пилотные школы». В конкретных случаях эти ограничения могут быть ослаблены или расширены автором задачи. Но вводимые ограничения должны быть тщательно взвешены, совершенно прозрачны для жюри и участника и в совокупности однозначны и непротиворечивы.
Типичный прием построения задачи — запретить операцию, функцию и предложить реализовать ее любыми оставшимися средствами. Тем самым выполняется и внутрипредметное моделирование в стиле методики учебника А. Г. Кушниренко и др.
Пример1.
Составить алгоритм вычисления А´В (для простоты при В>=0. А и В - целые). Кроме указанных выше ограничений запрещается умножение и деление «в лоб».
Решение на «старом» Бейсике может быть таким
| 10 'Умножение А * В без циклов и goto и * | |||
| 20 PRINT " Введите множители " |
| ||
| 30 INPUT А, В |
| ||
| 40 M1 = А | ‘передать параметры |
| |
| 50 М2 = В | ‘ |
| |
| 60 R = 0 | ‘накопитель произведения |
| |
| 70 GOSUB 110 | ‘ |
| |
| 80 PR = В | ‘забрать ответ |
| |
| 90 PRINT " произведение = "; PR |
| ||
| 100 END |
| ||
| 110 IF М2 = 0 THEM RETURN | ‘подпрограмма для R:=R+M1*M2 |
| |
| 120 М2 = М2 – 1 |
| ||
| 130 R = R + Ml | ‘умножение сводится сложению |
| |
| 140 GOSUB 110 | ‘цикл через рекурсию |
| |
| 150 RETURN | ‘-----à |
| |
Едва ли это олимпиадная задача, скорее — иллюстрация стиля программирования в условиях «искусственных» ограничений.
Если не запретить использование функций, возможен обход «сверху» в таком стиле:
В = INT(ЕХР(LOG(A) + LOG(B) + 0.5))
что тоже неплохо, но не выявит умения алгоритмизации. Это уже противоположный подход — использование готовых алгоритмов. Другой пример – постановка явно рекурсивной задачи при запрете рекурсии. Формально запрещены вызовы из подпрограмм, все остальное — можно, и особенно — желанное для некоторых GOTO...
Ограничения на «программирование»Признаком другого стиля мышления (назовем его пользовательским, в отличие от логико-алгоритмического «программистского») можно считать избегание программирования, стремление применить к своей задаче готовые средства, а если они не годятся — найти нестандартное, оригинальное применение другим доступным средствам, ведущее к цели, снова проявить способность к творчеству.
Характерной чертой такой деятельности является преобразование задачи, переход к другим типам данных, программ и команд. Например, целому числу можно сопоставить отрезок числовой оси или последовательность единиц.
Для такой деятельности необходимы:
1) образованность, знание явных и неявных возможностей различных готовых средств, как в «любимом» языке, так и вне его;
2) сформированность системно-комбинаторных мыслительных операций — видение предметов и явлений в целостности, взаимосвязях; умение строить несколько взаимодополняющих точек зрения на один и тот же объект, умение оперировать понятийными и орудийными средствами из различных дисциплин (так, например, с точки зрения алгебры функция есть соответствие, с точки зрения геометрии — кривая, с точки зрения информатики — алгоритм вычисления результата по заданному аргументу).
Для того чтобы проявить эти качества участника, нужно, так сказать, запретить ему программировать.
Это почти противоположно по отношению к ограничениям первого типа: чтобы выявить способности и опыт творчества в области алгоритмизации, мы вынуждали участника составлять довольно изощренные алгоритмы для решения «простых» задач (в примере — операция умножения). Теперь же он получает в распоряжение средства, но — кроме нужных для программирования. Теперь логично разрешить только линейные алгоритмы. Ведь соответствующая деятельность «пользователя» — это построение последовательности шагов по преобразованию среды. Его легко обеспечить через запрет логических выражений: именно проверки условий «расщепляют» алгоритм на циклы и ветвления. Для избежания программирования снова запрещаем машинные коды и ассемблер. Всё остальное — можно. Команду типа НЦ ДЛЯ или FOR тоже необходимо разрешить; она нужна для ввода таблиц (теоретически и в будущем может выполняться на N параллельных процессорах одно временно, как бы за один шаг).
В идеале решение задачи теперь должно быть представлено в виде линейной последовательности обращений к библиотечным и стандартным функциям, процедурам и программам (или даже в виде командного файла).
Уместно сказать теперь об электронных таблицах. Из встроенных в них циклов придется запретить итерационный цикл ДО заданной точности: он позволяет «почти все».
Приведем упрощенные примеры для иллюстрации задач второго типа. Первый пример — это умножение через логарифмы (см. выше).
Пример 2.
Нужно выяснить, лежит ли точка внутри контура, заданного координатами звеньев.
Решение (предложено школьниками).
Вывести цвет проверяемой точки, расположенной на экране.
Нарисовать на экране контур (цикл FOR!).
Залить его цветом.
Снова вывести цвет проверяемой точки.
Тонкие вопросы о «толстых» линиях контура на экране здесь не ставим: пример показывает нестандартное, лукавое и в то же время «наивное» решение через прямое моделирование задачи на экране,
Пример 3.
Нужно найти максимальное из двух чисел А и В. функции МАХ и MIN, естественно, запрещены.
Решение.
Max := (A+B+abs(A-B))/2.
Если забыть запретить функцию MIN, то возможен «обход сбоку»:
Max := A+B-min(A,B).
Решения подобных задач не сводятся к составлению, алгоритмов, полученные алгоритмы всего лишь линейные, но отличаются ярким творческим началом.
Проведение олимпиад по информатике на основе тестовВ последнее время всё чаще поднимается вопрос о методике преподавания олимпиад по информатике. Традиционные олимпиады, как правило, ориентированы на проверку программистских навыков и предполагают наличие у учеников обширных познаний в математике и языках программирования, что является приоритетом физико-математических школ. Что же делать основной массе увлечённых ребят? Как организовать олимпиаду для детей, обучающихся в разных школах, по разным программам, изучающих разные языки программирования (а может, не изучающих их?), работающих на «разношёрстной» вычислительной технике? Из этого положения можно найти выход, если проводить отдельно олимпиаду по программированию и информатике. В некоторых школах такие олимпиады проводятся на основе тестов.
Вопросы тестов подобраны таким образом, что позволяют проверить общий уровень подготовки учащихся и дают возможность решить главные проблемы, возникающие при проведении по информатике:
· разнообразие вычислительной техники, находящейся в школах;
· различный уровень преподавания информатики;
· большой спектр алгоритмических языков, изучаемых в школах;
· ограничение количества вычислительной техники в школе, проводящей олимпиаду, а значит и количества участников олимпиады.
Принцип тестирования позволяет легко и быстро проверить работы учащихся, а значит, в короткий срок определить победителей.
Предлагаемые тесты разбиты по возрастным группамVII – IX и X – XI классы. При подсчёте баллов рекомендуется использовать принцип: каждый правильный ответ – «+1» балл, неправильный ответ – «-1» балл (если не знаешь ответа, не пытайся угадать его) и «0» баллов за вопрос, на который ответа нет.
В данном реферате предлагается вариант тестового задания олимпиады по информатике для старшей возрастной группы.
Тестовые вопросы олимпиады по информатике для старшей возрастной группы (X-XI классы)
1. Может ли одно и тоже явление иметь разные модели?
1) Да;
2) Нет.
2. Какое минимальное количество двоичных разрядов потребуется для того чтобы закодировать прописные и строчные буквы русского алфавита и арабские цифры?
1) 2;
2) 3;
3) 4;
4) 5;
5) 6;
6) 7;
7) 8.
3. В текущем каталоге находятся программы LOGIN.BAT, LOGIN.EXE, LOGIN.COM. Какая программа будет выполнена, если вы наберёте в командной строке LOGIN?
1) LOGIN.BAT
2) LOGIN.EXE
3) LOGIN.COM
4. Последовательность записей, размещённых на каких-либо запоминающих устройствах, рассматриваемая в процессе пересылки и обработки как единое целое, называется:
1) файлом;
2) массивом;
3) программой.
5. Гипертекст – это:
1) очень большой текст;
2) структурный текст, в котором можно осуществлять переходы по «горячим» словам;
3) текст, набранный на компьютере;
4) текст, в котором используется шрифт максимального размера.
6. Преимущество двоичной системы счисления состоит в том, что:
1) двоичный код позволяет экономить память компьютера;
2) электронные элементы с двумя состояниями потребляют меньше электроэнергии;
3) электронные элементы с двумя состояниями наиболее просты в конструктивном исполнении.
7. Что можно рассматривать как алгоритм?
1) инструкцию по пользованию метрополитеном;
2) схему метро;
3) правила пользования телефоном-аппаратом;
4) телефонный справочник.
8. Минимальным объектом в текстовом редакторе является:
1) символ;
2) слово;
3) пиксель;
4) абзац;
5) файл.
9. Какое устройство компьютера может оказать вредное воздействие на здоровье человека?
1) гибкий диск;
2) системный блок;
3) монитор;
4) клавиатура;
5) жесткий диск;
6) блок питания.
10. Тексту объёмом в 2Кбайта соответствует:
1) символ;
2) абзац;
3) страница;
4) книга.
11. Основным элементом электронной таблицы является:
1) ячейка;
2) столбец;
3) строка;
4) таблица.
12. Результатом деления 1101101 на 110 в системе счисления с основанием 2 является:
1) 10010, остаток 1;
2) 1001, остаток 1;
3) 10110;
4) 1011.
13. В электронной таблице выделен участок A2:B4. Сколько ячеек он занимает?
1) 3;
2) 4;
3) 5;
4) 6.
14. Расшифруйте значение строки:
486DX2/66/4/256/210/3,5''/5,25''/2s1p/512/14’’SVGA.28.
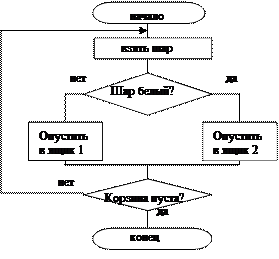
15. Какое минимальное количество шаров должно быть в корзине, чтобы программа работала верно?
1) любое;
2) ни одного;
3) один.
16. Основным элементом базы данных является:
1) запись;
2) форма;
3) поле;
4) таблица;
5) тип.
17. Принцип открытой архитектуры означает, что:
1) компьютер сделан единым неразъёмным устройством;
2) возможна лёгкая замена устаревших частей компьютера;
3) новая деталь компьютера будет совместима со всем тем оборудованием, которое использовалось ранее.
18. Структура базы данных изменится, если:
1) добавить или удалить запись;
2) поменять местами запись;
3) отредактировать строку;
4) добавить или удалить поле.
19. Электронная почта (E-mail) позволяет передавать:
1) сообщения;
2) файлы;
3) сообщения и приложенные файлы;
4) WWW-страницы.
20. Модем обеспечивает:
1) модуляцию (преобразование двоичную информацию в аналоговую);
2) демодуляцию (преобразование аналоговой информации в двоичную);
3) модуляцию и демодуляцию;
4) усиление сигнала.
21. Кэш-память жесткого диска предназначена для:
1) увеличения объёма жесткого диска;
2) ускорения доступа к данным на жестком диске;
3) ускорения чтения информации из оперативной памяти;
4) увеличение объёма видеопамяти.
22. Микропроцессор служит для:
1) сложения двоичных чисел;
2) перевода чисел из двоичной системы счисления в десятеричную;
3) оперативного запоминания команд;
4) распознавания кода программы.
23. На логическом диске А задан полный путь к файлу \DOC\PROBA.TXT. Каково полное имя файла?
1) C:\DOC\PROBA.TXT;
2) A:\PROBA.TXT;
3) DOC\PROBA.TXT;
4) TXT;
5) A:\DOC\PROBA.TXT.
24. Какой логической функции соответствует следующая таблица истинности:
| A | B | F |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
1) F=
2) F=
3) F=
4) F=
25. Память какого вида используется для записи и чтения информации?
1) ОЗУ;
2) ПЗУ;
3) гибкие диски;
4) жесткие диски.
26. Кто является основоположником отечественной вычислительной техники?
1) Д. Н. Лозинский;
2) С. А. Лебедев;
3) А. А. Марков;
4) М. Р. Шура-Бура.
27. Двоичное кодирование одного символа (буквы) требует количества информации, равное:
1) 1 биту;
2) 1 байту;
3) 4 битам;
4) 1 килобайту.
28. Какая логическая функция тождественна логической функции
1) 
2) 
3) 
4)
5) 
29. В компьютер Pentium (64-разрядная шина данных и 32-разрядная шина адреса) установлена память 16 Мбайт. Каково адресное пространство этого процессора?
1) 264;
2) 232;
3) 16 Мбайт;
4) 64 бит.
30. Какие файлы соответствуют маске ??Р*.А??
1) PPEPSI.ABC;
2) PEDDY.A1;
3) PEPPER.ARJ;
4) PEPSI.A1;
5) PEPPY.A7F;
6) CAPITAL.A3A;
7) SUPPORT.A1.
31. Какая часть текста программы не влияет на ее выполнение?
1) оператор;
2) директива;
3) комментарий;
4) скобки.
32. Американский математик – автор теории игр:
1) Джон Нейман;
2) Бил Гейтс;
3) Стив Джобс.
33. Каково греческое распространённое название «саламанской доски»?
1) Суан-пака;
2) серобяна;
3) абак.
34. Состояние системы, при котором она перестаёт выдавать результаты и реагировать на запросы извне:
1) зависание;
2) зацикливание;
3) отключение монитора.
35. Умножьте два числа 121 и 21 в системе счисления с основанием 3.
36. Какая программа синтаксически проверяет оператор и тут же его выполняет?
1) компилятор;
2) интерпретатор;
3) редактор;
4) отладчик.
37. Каково количество цифр в двоичной системе счисления?
1) 10;
2) 16;
3) 8;
4) 2.
38. Переменная задана, если известны её:
1) тип;
2) тип, имя, значение;
3) имя, значение,
4) значение.
39. Во время начальной загрузки DOS пользуются двумя текстовыми файлами – CONFIG.SYS и AUTOEXEC.BAT. Какой из этих файлов загружается первым?
1) CONFIG.SYS;
2) AUTOEXEC.BAT.
40. Основная технологическая цепочка решения задачи с использованием компьютера:
1) построение модели – постановка задачи – разработка и исполнение алгоритма – анализ результатов;
2) постановка задачи - построение модели – разработка и исполнение алгоритма – анализ результатов;
3) постановка задачи – разработка и исполнение алгоритма - построение модели – анализ результатов.
41. Задано дерево каталогов:
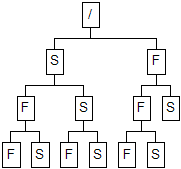Какой каталог будет текущим после выполнения следующих команд:
CD\
CD F
CD F\S
CD ..\..
CD \S\F
CD ..\S
1) \S\F\S;
2) \F\S\F;
3) \S\S;
4) \S\S\S;
5) \F\F\S.
Заключение
Итак, постановка олимпиадных задач как задач на преодоление ограничений позволяет, в принципе; выявить и способности в области алгоритмизации, и образованность, и пользовательский стиль мышления. А ученик, успешно преодолевающий системы ограничений различных типов, — законный победитель олимпиады. При замене и, особенно, при выключении «рентгеновского аппарата» ограничений на олимпиаде следующего уровня его способности раскроются скачком на полной мере, так как именно опыт преодоления ограничений послужил формированию у него активных, системных и пробных знаний.
При такой постановке дела подготовка к олимпиаде становится для школьника естественным продолжением базового курса информатики даже бед специальных занятий с учителем. Вводя для себя различные ограничения и преодолевая их, он может заниматься тем же, что и весь класс на том же уроке, и по той же теме, что и все остальные. Но решать задачи он будет не только простейшим путём, как большинство, но и по-своему: «вынужденно-творческим» методом. Нужно лишь сообщить ему об этом пути независимого самосовершенствования. Это снимает и проблему индивидуализации обучения при фронтальных формах работы учителя с классом через «озадачивание» сильных учащихся.
В заключение — практический совет разработчикам задач: можно предварительно проверять целостность системы ограничений, порождающей задачу, привлекая для попытки их обхода одаренного и образованного школьника, или студента. Уместно также сказать, что для данной проверки полностью задачу раскрывать не обязательно.
Литература
o Бочкин А. И. Информатика: Справочник по решению задач повышенной трудности. ВГПИ, Витебск, 1994
o Информатика и образование, 1997, №4
o Информатика и образование, 1997, №5
o Информатика и образование, 1997, №8
o Информатика и образование, 1996, №6
o Педагогика, 2000, №9
0 комментариев