Метод половинного деления

Министерство общего и профессионального образования

Стерлитамакский Государственный Педагогический Институт

кафедра информатики и вычислительной техники

КУРСОВАЯ РАБОТА

на тему:

«Метод половинного деления в школьном курсе информатики»

Работу выполнили студенты 42 группы ФМФ: Дубовицкий Сергей и Волков Антон

Руководитель: доцент Хусаинова Г.Я.

Стерлитамак 2001

 

ПлАН:

Введение

Метод половинного деления................................................................................................................................................... 4

Задача......................................................................................................................................................................................................... 4

Алгоритм................................................................................................................................................................................................... 6

Блок схема................................................................................................................................................................................................. 7

Заключение............................................................................................................................................................................................... 8

Литература................................................................................................................................................................................................. 9

Приложение

 
Введение Целью данной курсовой работы является раскрытие содержания темы «Метод половинного деления» и дальнейшее ее закрепление путем выполнения лабораторной работы и практических заданий.

Одной из главных задач в обучении является развитие творческих и исследовательских способностей учащихся. На уроках информатики применение компьютеров позволяет учащимся заниматься исследовательской работой при решении задач из различных областей (например, физические, математические, экономические задачи). При этом они должны научиться четко формулировать задачу, решать ее и оценивать полученный результат.

Использование новых информационных технологий позволяет решать некоторые задачи нетрадиционными способами, а также решать прикладные задачи, которые ранее не могли рассматриваться в силу сложности математического аппарата. Так, в школьном курсе математики учащиеся рассматривают уравнения, которые имеют точные решения. Однако в реальной практике решение большинства уравнений не может быть записано в явном виде. Их решение находится только приближенными методами. Ранее способы решения таких уравнений рассматривались после изучения одного из алгоритмических языков. Во-первых, разрабатывали алгоритм метода решения (например, итерации, половинного деления). Во-вторых, составляли программу и использовали ее для получения решения и его исследования. Труднее было при изучении темы "Моделирование", когда рассматривали задачи оптимизации. Задачи должны были быть довольно простыми, допускающими только одну поисковую переменную.

В школьном курсе информатики метод половинного деления изучается в 11 классе на 42 уроке при изучении раздела «Компьютерное моделирование», закрепляется тема на 43 уроке в виде Лабораторной работы.

Метод половинного деления

Решение алгебраического уравнения. Для численного решения алгебраических уравнений существует множество способов. Среди самых известных можно назвать метод Ньютона, метод Хорд, и «всепобеждающий» метод Половинного Деления. Сразу оговоримся, что любой метод является приближенным, и по сути дела лишь уточняющим значение корня. Однако уточняющим до любой точности, заданной Нами.

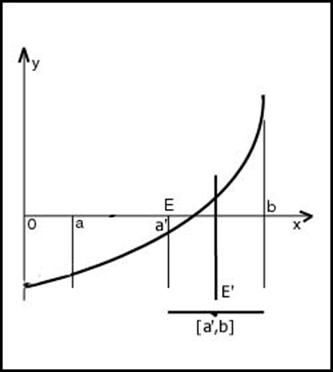
Метод половинного деления или дихотомии (дихотомия - сопоставленность или противопоставленность двух частей целого) при нахождении корня уравнения f(x)=0 состоит в делении пополам отрезка [a; b], где находится корень. Затем анализируется изменение знака функции на половинных отрезках, и одна из границ отрезка [a; b] переносится в его середину. Переносится та граница, со стороны которой функция на половине отрезка знака не меняет. Далее процесс повторяется. Итерации прекращаются при выполнении одного из условий: либо длина интервала [a; b] становится меньше заданной погрешности нахождения корня ε, либо функция попадает в полосу шума ε1 – значение функции сравнимо с погрешностью расчетов.

Сначала поставим задачу. Дана монотонная, непрерывная функция f(x), которая содержит корень на отрезке [a,b], где b>a. Определить корень с точностью ε, если известно, что f(a)*f(b)<0

Дано уравнение вида:

f(x)=0; (1)

необходимо найти удовлетворяющие ему значения x.

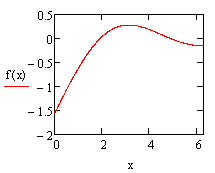
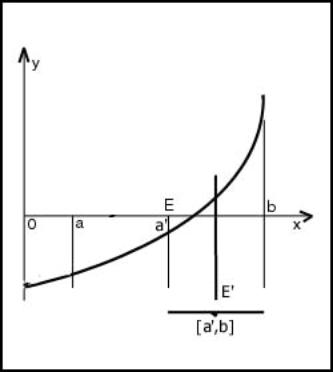
Итак, приступим к решению. Первым делом, определимся, что значит f(x)=0. Посмотрите на рис.1. На нем изображен график некоей функции. В некоторых точках этот график пересекает ось абсцисс. Координаты x этих точек нам и нужно найти. Если вид уравнения простой или стандартный, например, квадратное уравнение или линейное, то применять численный метод здесь совершенно ни к чему. Но если уравнение у нас такое:

f(x)=x3-14x2+x+ex; (2)

то ни в каком учебнике вы не найдете метода аналитического решения этого кошмара. Здесь и приходит на помощь непобедимый численный метод. Метод половинного деления. Из самого названия метода можно предположить, что нам понадобится что-то делить пополам.

Ученикам метод половинного деления можно преподнести в виде решения задачи.

Задача

Идет осада неприятельской крепости. На некотором расстоянии от нее установили новую пушку. Под каким углом к горизонту надо стрелять из этой пушки, чтобы попасть в заданный участок крепостной стены.

Над моделью этой задачи физики изрядно поработали. Оно и понятно: ведь многие научные задачи, как и эта, возникали прежде всего в военном деле. И решение этих задач почти всегда считалось приоритетным.

Какие же факторы принять за существенные в этой задаче? Поскольку речь идет о средневековье, то скорость снаряда и дальность полета невелики. Значит можно считать несущественным, что Земля круглая (помните обсуждение в параграфе 27), и пренебречь сопротивлением воздуха. Остается единственный фактор – сила земного притяжения. В этом случае, как вы знаете из физики, горизонтальное (х) и вертикальное (у) смещение снаряда за время t описывается формулами

,

где g – ускорение свободного падения, v – начальная скорость снаряда, α – угол наклона пушки к горизонту. Эти формулы задают математическую модель полета снаряда. Нас же интересует, на какой высоте окажется снаряд, пролетев расстояние S.

Впрочем, это нетрудно найти. Выразим время полета снаряда на расстояние S из первой формулы:

,

и подставим во вторую:

Следуя нашей задаче, нам требуется найти такое значение угла наклона α, чтобы снаряд, пролетев заданное расстояние S, попал на нужную высоту Н.

Математик тут бы сказал, что надо решить уравнение. Мы тоже будем решать, только приближенно и очень похоже на то, как делают настоящие артиллеристы. Они же поступают следующим образом: производят несколько выстрелов, беря цель «в вилку», т.е. одно попадание выше цели, а другое ниже. Затем делят пополам угол между этими выстрелами, и при стрельбе под таким углом снаряд ложится к цели намного ближе. Но если все же не попали, то новую «вилку» снова делят пополам и т.д.

Мы заранее можем указать «вилку» для угла: 0 и π/4 (мы надеемся, что вы помните какой угол имеет радианную меру π/4 и чему приближенно равно π). А дальше будем делить пополам эту «вилку» и смотреть, куда попадает снаряд, пока не добьемся нужного результата.

Как же долго нам придется вести «пристрелку», чтобы получить угол α, с нужной точностью? Чтобы ответить на этот вопрос, отвлечемся от нашей задачи и сформулируем на чисто математическом языке, что и как мы находили.

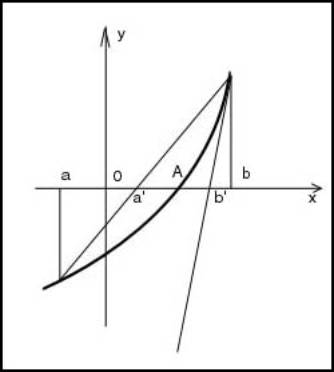
Нам даны некоторая функция f(x) и отрезок [a;b], причем на концах этого отрезка эта функция принимает значения противоположных знаков. Если функция непрерывна, т.е. ее график – непрерывная линия, то ясно, что график функции пересекает ось абцисс в некоторой точке с отрезка [a;b], как показано на рисунке 1. Иными словами, f(c)=0, т.е. с - корень уравнения f(x)=0.

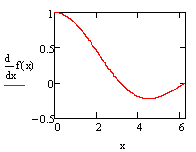
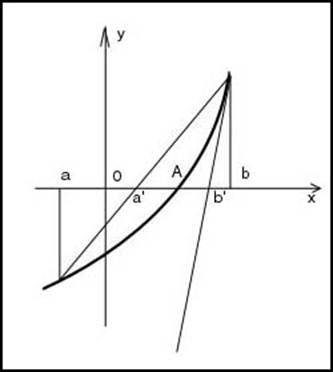
Как же предлагается находить этот корень? А вот так. Делим отрезок [a;b] пополам, т.е. берем середину отрезка а+b/2. В этой точке вычисляем значение функции f(x) (рис. 2). Если это значение 0, то корень найден; если нет, то оно имеет тот же знак, что и значение на одном из концов отрезка [a;b]. Тогда этот конец заменям точкой а+b/2. Новый отрезок тоже содержит корень уравнения f(x)=0, поскольку на его концах функция f(x) снова имеет разные знаки. Однако этот отрезок в 2 раза короче предыдущего. И самое главное – с ним можно поступить точно так же. со следующим отрезком еще раз проделать то же самое и т.д. поскольку длина отрезка каждый раз уменьшается вдвое, мы можем получить отрезок сколь угодно малой длины, внутри которого содержится корень уравнения f(x)=0. Например, если исходный отрезок был [3;4], т.е. имел длину 1, то через десять шагов мы получим отрезок длиной . Это означает, что концы отрезка дают нам приближенное значение корня с точностью, равной длине отрезка: левый конец отрезка – приближенное значение корня с недостатком, правый конец – приближенное значение корня с избытком.

Фактически мы сейчас сформулировали метод приближенного решения уравнения f(x)=0. Его можно было бы назвать методом артиллерийской пристрелки. Но математики называют его методом половинного деления.

Далее ученикам предлагается записать алгоритм и блок-схему нахождения корня уравнения с помощью метода половинного деления.

Алгоритм

 

1)  Найдем середину отрезка [a; b]: c=(a+b)/2;

2)  Вычислим значения функции в точках a и c и найдем произведение полученных значений: d=f(c)ּf(a);

3)  Если d>0, то теперь точкой a станет c: a=c; Если d<0, то точкой b станет c: b=c;

4)  Вычислим разность a и b, сравним ее с точностью ε: если |a-b|> ε, то идем в пункт 1) если нет, то корень с нужной нам точностью найден, и он равен: x=(a+b)/2;

Блок- схема

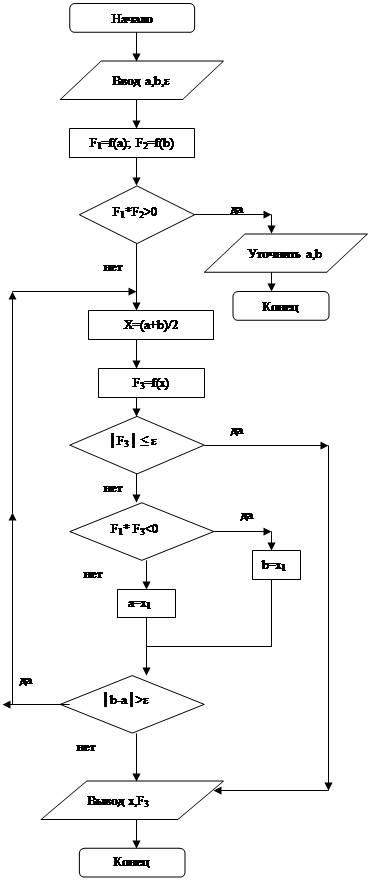
Заключение

Информатике трудно существовать в школе как отдельной науке, она должна помогать другим учебным предметам в развитии познавательного интереса к предмету, в решении логических задач, в обработке результатов лабораторных работ и индивидуальных практических заданий. Школьники начинают испытывать удовлетворение, замечая, что элементы математики и информатики имеют реальное воплощение в физических процессах.

Математика является необходимой базой, которая позволяет глубже вникнуть в суть описываемых физических явлений и закономерностей. Hа уроках физики развиваются и конкретизируются многие математические понятия: функции, графики, уравнения, неравенство, производная, интеграл, вектор и др. Это требует согласованных действий от учителя физики и математики при формировании общих понятий.

В применении информатики к преподаванию других предметов используются в основном две формы работы: привлечение программных средств для контроля знаний учащихся и работа учащихся с обучающими программами. В стороне остаются возможности составления программ самими учащимися для решения тех или иных задач, например, из области физики. Среди методистов распространено мнение, что подобная работа в школе возможна лишь на высоком уровне (в специализированных классах) из-за слабой подготовки учащихся в области программирования. Однако при согласованных действиях преподавателей физики, математики и информатики этот недостаток может быть легко выполнен. В частности успешным оказывается проведение уроков по теме "Движение тела под действием силы тяжести при начальной скорости управления горизонтально или под углом к горизонту", изучаемой в курсе физики 9 класса совместно с учителем информатики. В курсе информатики Учащимся предлагается лабораторная работа "Артиллериская задача". При выполнении данной работы учитель отрабатывает навыки программирования, изучает метод дихотомии (половинного деления). При этом приходится решать задачу физически, т.е. возникают трудности по применению формул физики. Таким образом затмевается главная цель урока по информатике: формирование умений и навыков решения задач методом половинного деления с использованием ЭВМ. Поэтому здесь и необходимо проведение интегрированных уроков по физике и информатике при решении задач. Тем более, что в Сборник задач по физике для 9-11 классов (переизданного в 1992 г.), автором которого является А.П. Рымкевич, включены программируемые задачи, которые для решения требуют знаний по физике и информатике.

Литература

1.   Гейн А.Г., А.И. Сенокосов, Н.А. Юнерман «Информатика: учебное пособие для 10-11 классов». М.: Просвещение, 2001.

2.   Гейн А.Г., В.Г. Житомирский, Е.В. Линецкий, М.В. Сапир, В.Ф. Шолохович «Основы информатики и вычислительной техники». М.: Просвещение, 1992.

3.   Симонович С., Г. Евсеев. «Практическая информатика: Учебное пособие для средней школы. Универсальный курс». – М.: Аст-пресс: Инфорком-пресс, 2001.

4.   Сеть Internet

Приложение  

Тематическое планирование уроков в 11 классе (68 часов).

№	Тема урока	Краткое содержание
1	Циклическая форма организации действий.	Циклы "до" и "пока". Вложенные и последовательные циклы.
2	Использование циклических структур при вычислении суммы произведения или количества множества произвольных числовых констант.	Рассмотрение таблицы предписаний для вычисления суммы произведения и количества множества чисел.
3	Циклическая структура как частный случай разветвляющегося алгоритма.	Решение задач, представляющих циклическую структуру с помощью операторов IF… THEN… GOTO. Операторы WHILЕ и WEND.
4	Цикл с параметрами.	Цикл для каждого и его параметры. Операторы FOR… TO… NEXT в цикле с параметрами.
5	Вводный инструктаж по ТБ.	Повторение правил ТБ для работы в компьютерном классе.
6	Лабораторно-практическая работа № 1 "Разработка электронных часов на экране компьютера".	Ввод в ПК программы "Электронные часы" и исследование параметров цикла "для каждого".
7	Закрепление уроков № 1 - 5.	Решение задач, имеющих в своей структуре один цикл.
8	Лабораторно-практическая работа № 2 "Использование операторов цикла для каждого при решении задач на ПК".	Решение на ПК задачи, имеющих в своей структуре один цикл.
9	Закрепление уроков 1 - 5.	Решение задач, имеющих в своей структуре один цикл.
10	Лабораторно-практическая работа № 3 "Использование операторов цикла для каждого при решении задач на ПК".	Решение на ПК задач, имеющих в своем составе только один цикл.
11	Самостоятельная работа по темам уроков 1 - 5.
12	Связь программирования с математикой.	Развитие графического мышления для построения графиков функций (на Бейсике) на экране ПК.
13	Лабораторно-практическая работа № 4 "Использование операторов графики языка Бейсик для построения графиков на экране монитора".	Решение задач на ПК на построение графиков функций.
14	Структурный подход к решению задач с использованием циклов и ветвлений.	Способы построения сложных алгоритмических структур. Последовательные структуры и структуры с вложением.
15	Переход от неструктурного алгоритма к структурному.	Способы перехода - размножение блоков или ввод дополнительной переменной.
16	Закрепление уроков 13 - 14.	Решение задач, приводящих к структурному виду алгоритмы, не являющиеся структурными.
17	Лабораторно-практическая работа № 5 "Использование сложных алгоритмических конструкций в составлении программ на Бейсике".	Решение на ПК задач, имеющих в своем составе сложные алгоритмические структуры.
18	Закрепление уроков 13, 14	Решение задач, имеющих в своем составе сложные алгоритмические структуры.
19	Контрольная работа по теме "Структурное программирование".
20	Табличный способ организации данных.	Таблицы. Типы. Одномерный и двумерный массив. Операции с массивами.
21	Обработка массивов на языке Бейсик.	Ввод массивов с помощью операций LET, INPUT, DATA-READ, задание элементов массива случайным образом, вывод элементов массива.
22	Закрепление уроков 20, 21	Решение задач на обработку массивов на Бейсике.
23	Лабораторно-практическая работа № 6 "Обработка массивов на Бейсике".	Решение задач с табличной организацией числовых данных.
24	Закрепление уроков 20,21.	Решение задач на обработку массивов на Бейсике.
25	Лабораторно-практическая работа № 7 "Обработка массивов на Бейсике".	Решение задач с табличной организацией числовых данных.
26	Самостоятельная работа по темам уроков 20 - 21.
27	Обработка текстовых данных.	Действия над текстовыми величинами, операции и функции символьных переменных.
28	Закрепление уроков 27	Решение задач на обработку текстовых данных.
29	Лабораторно-практическая работа № 8 "Использование операций и функций символьных переменных при решении задач на ПК".	Решение задач на обработку текстовых данных.
30	Закрепление урока 27	Решение задач на обработку символьных массивов.
31	Лабораторно-практическая работа № 9 "Обработка символьных массивов на ПК".	Решение задач на обработку символьных массивов.
32	Самостоятельная работа по темам уроков 27 - 31.
33	Сортировка числовых массивов.	"Пузырьковая" сортировка , минимаксная сортировка.
34	Закрепление урока 33.	Решение задач, включающих в себя сортировку данных.
35	Лабораторно-практическая работа № 10 "Использование методов сортировки при обработке данных".	Решение задач на обработку данных методами сортировки.
36	Вспомогательные алгоритмы. Подпрограммы.	Основные и вспомогательные алгоритмы. Метод последовательной детализации.
37	Закрепление урока 36.	Решение задач, включающих в себя вспомогательные алгоритмы.
38	Лабораторно-практическая работа № 11 "Использование подпрограмм при решении задач на ПК".	Решение задач, включающих в себя подпрограммы.
39	Определение нестандартных функций.	Оператор DEFFEN и его назначение. Решение значений нестандартных функций.
40	Лабораторно-практическая работа № 12 "Использование оператора DEFFN при решении нестандартных функций".	Решение значений нестандартных функций и возможность избежания повторений одинаковых выражений в Бейсике.
41	Закрепление уроков 39 - 40.	Решение задач, вычисляющих значения нестандартных функций и использующих возможность избежания повторений одинаковых выражений на Бейсике.
42	Метод половинного деления.	Приближенное вычисление значений непрерывных функций.
43	Лабораторно-практическая работа № 13 "Использование метода половинного деления при решении задач на ПК".	Решение задачи по нахождению значений непрерывных функций
44	Метод трапеций.	Приближенное вычисление определенного интеграла.
45	Лабораторно-практическая работа № 14 "Использование метода трапеций для вычисления определенного интеграла на ПК".	Приближенное вычисление определенного интеграла.
46	Метод Монте-Карло. Вычисление p методом Монте-Карло.	Приближенное вычисление площадей сложных фигур.
47	Лабораторно-практическая работа № 15 "Использование метода Монте-Карло для вычисления площадей сложных фигур на ПК".	Решение задач по определению площади сложных фигур.
48	Контрольная работа.
49	Информационные технологии. Технология текстовой информации.	Этапы развития информационных технологий. Текстовый редактор, среда ТР "WORD". Режимы его работы.
50	Технология обработки графической информации.	Графический редактор. Среда ТР "PAINT". Графические примитивы, функции ГР, режимы его работы.
51	Технология обработки числовой информации.	Электронные таблицы. Табличные процессоры. Среда ТП. Данные в ЭT "EXСEL", режимы ее работы и системные команды.
52	Технология хранения, поиска и сортировки информации.	Базы данных. Информационные системы. Типы организации данных.
53	Система управления базами данных.	СУБД, режимы работы с базами данных.
54	Технология мультимедиа.	Мультимедийные приложения. Задачи медиасерверных систем. Аппаратные и программные средства мультимедиа. Конфигурация мультимедиа ПК.
55	Самостоятельная работа
56	Компьютерные вирусы.	Типы вирусов в ПК, меры профилактики компьютерных вирусов.
57	Компьютерные телекоммуникации.	Средства телекоммуникаций. Серверы. Режимы работы серверов.
58	Локальные, отраслевые, региональные и глобальные компьютерные сети.	Виды сетей. Составные части ЛВС. Топологии ЛВС.
59	Глобальная компьютерная сеть. Сеть Интернет как пример глобальной телекоммуникационной сети.	Сети RELCOM и INTERNET . Типология глобальной сети. Компоненты процесса передачи информации по глобальной сети.
60	Информационные ресурсы и сервисы сети Интернет.	Сетевые технологии. Электронная почта.
61	Электронная доска объявлений и телеконференции. Файловые архивы и дополнительные услуги Интернет.	Услуги электронной доски объявлений. Назначение телеконференций. Содержание файловых архивов.
62	Гипертекст. Технология WWW. Гиперсвязи и всемирная паутина.	Историческая справка. Текстовые графы.
63	Самостоятельная работа по темам уроков 56 - 62.
64	Правовые аспекты информатики.	Авторское и имущественное право. Виды компьютерной преступности.
65	Информатизация общества.	Информационно-компьютерная революция. Концепция современного общества.
66	Контрольная работа.
67	Анализ результатов контрольной работы.
68	Заключительный урок в 11 кл.	Выставление оценок за год и за курс.

Задачи

1. Дано уравнение 2.2х-2^х=0. Найти оба корня уравнения методом половинного деления и методом итераций.

Решение:

Интервал (а=0, b=4) на котором лежат корни находится из графика (рис.1.):

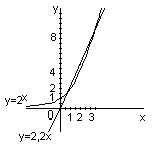(рис.1.)

(метод половинного деления)

INPUT "Ведите погрешность"; e

a = 0: b = 2: k = 0: d = 0

start: z = 2.2 * a - 2 ^ a

div: x = (a + b) / 2

IF (b - a) / 2 <= e THEN GOTO yes

y = 2.2 * x - 2 ^ x: k = k + 1

IF z * y > 0 THEN a = x: z = y ELSE b = x

GOTO div

yes: PRINT "X="; x, "K="; k

IF d = 0 THEN a = b: b = 4: d = 1: GOTO start

Результаты вычислений:

Ведите погрешность? 0.001

X= .7802734 K= 10

X= 2.400841 K= 21

2. Составить алгоритм и программу на языке Turbo Basic, которая позволяет компьютеру угадать число, загаданное пользователем (от 1 до 64) не более, чем за 7 попыток.

3. Задана функция у(х) = x ×p × exp(-x) - x × 0.22.

а) Методом половинного деления опpеделить коpень уpавнения y(х) = 0 на интеpвале (0 , 10) с точностью до 0.001.

б) Методом половинного деления найти максимум функции на интервале (0 , 10) с точностью до 0.001 по аpгументу.

4. а) Для уравнения x³ – 3x + 3 = 0 определите два числа, образующие “вилку” для корня этого уравнения . сколько раз придется выполнить деление пополам для найденного вами отрезка, чтобы получить корень с точностью 0,01? А с точность 0,001?

б) Выполните задание а) для уравнения 2^х=3х.

в) Выполните задание а) уравнения cos x=x.

Лабораторная работа

Компьютерным средством, с помощью которого мы будем решать задачу, служит электронная таблица. Подготовим ее заполнение.

A	B	C	D
Расстояние S	3000	Точность	0.001
Высота H	1		C4-B4
Начальная скорость	200		B3^2
Угол	0	0	(B4+C4)/2
Отклонение от цели	B2-B1*(D5-9.8*B1*(1+D5^2)/(2*D3))		tg(D4)

В клетках B4 иС4 записаны значения угла (в радианах), составляющие «вилку»; в клетке D4 – значение угла, для которого будет вычисляться отклонение от цели. Кроме того, чтобы по нескольку раз не вычислялось одно и оже число (а на это уходит время), в клктке D5 записан тангенс очередного значения угла наклона пушки к горизонту, а в клетке D3 – квадрат начальной скорости (поскольку в электронной таблице все формулы записываются в «линейку», то и для показателя степени используется не верхний индекс, а специальный знак - ^). С той же целью – ускорение вычислений – мы в формуле оклонения заменили 1/cos²a на 1+tg²a. Заполнение остальных клеток понятно из таблицы. Значение g взято 9,8 м/с², расстояние S=3 км, а высота Н=1 м. Точность вычисления равна 0,001.

Сначала проверим, правильно ли мы выбрали отрезок для корня. В таблице в клетках B4 и С4 записаны нули, поэтому отклонение подсчитывается для a=0. Как видите, на левом конце отрезка отклонение положительно.

Запишите теперь в клетках В4 и С4 число 0,75 (это – приближенное значение для p/4). Теперь отклонение оказалось отрицательным.

(1)   Приступим к нахождению нужного угла a. Запишите в клетке В4 чило 0, и электронная таблица тут же вычислит значение отклонения в точке 0,75/2.

Это значение оказалось положительным. Следовательно, значением 0,75/2 надо заменить левый конец отрезка, записанный в клетке В4.

(2)   Меняем 0 на значение клетки D4. Отклонение стало отрицательным.

Следовательно, надо поменять значение клетки С4 на значение клетки D4. Действуйте!

(3)   Продолжайте поиск корня, пока не получится заданная точность (напоминаем, что индикатором точности служит клетка D2, в которой вычисляется длина текущего отрезка).

Другие варианты:

I.

A	B	C	D
Расстояние S	4000	Точность	0.001
Высота H	1		C4-B4
Начальная скорость	220		B3^2
Угол	0	0	(B4+C4)/2
Отклонение от цели	B2-B1*(D5-9.8*B1*(1+D5^2)/(2*D3))		tg(D4)

II.

A	B	C	D
Расстояние S	3000	Точность	0.0001
Высота H	2		C4-B4
Начальная скорость	220		B3^2
Угол	0	0	(B4+C4)/2
Отклонение от цели	B2-B1*(D5-9.8*B1*(1+D5^2)/(2*D3))		tg(D4)

Ш.

A	B	C	D
Расстояние S	2000	Точность	0.01
Высота H	1,5		C4-B4
Начальная скорость	250		B3^2
Угол	0	0	(B4+C4)/2
Отклонение от цели	B2-B1*(D5-9.8*B1*(1+D5^2)/(2*D3))		tg(D4)